#ElementalFlow

[fluxsci]

Significance: Elemental Flow

The atom is arguably the most important particle in the study of science, as it makes up every substance, seen and unseen, in the universe. It is made of several, smaller particles, including protons, neutrons and electrons. Although protons and neutrons, which are made of smaller, even more fundamental particles, are interesting parts of the atom to study, the Elemental Flow arc takes a look at the negatively-charged electron.

Without electrons, no substance would exist as we know it today, including those substances that make up our bodies. The primary function of electrons is to give the atom a type of currency that can be used to control its energy. This makes electrons important for stability of the atom and, by extension, the stability of every substance in the universe.

To be as stable as possible, atoms seek to complete their outermost electron shell, which is the region farthest outside of the atom’s core. Although the Periodic Table of Elements informs you of exactly how many electrons are needed to complete a shell, there is science - complex science - behind its organization. This complex science is called quantum mechanics, which explains why electrons interact with each other in the way that they do.

Quantum mechanics shows an important part of the study of science that will stick with us throughout the journey through the following arcs: there are many things we know, but there are many more things that we do not know.

—

Start the Elemental Flow arc or see a summary of the arc, here.

Catch Flux's 2019 Agenda here. For more thought-provoking content, join our mailing list!

[natty373]

🌈❤️🌈 One ☝️ thing i love about teaching Life Refinement Therapies is that each time we share our truth about our elemental connection to source, refining our inner energies to flow, the greater we feel collectively, as well as individually ➡️ here we strengthen our connection to our cells 🧬 each other ⚛️ & expand the truth energy at large .... 🌍 yoga is union - let us all grow and evolve together .... namaste 🙏🏽 • • • #flow #energy #connection #source #gentle #embodiedflow #engagement #elementalflow #pranavinyasa #nature #naturalhealth #naturesmedicine #love #yoga #union #liferefinementtherapies (at Austinmer, New South Wales, Australia) https://www.instagram.com/p/B04pLlSgT8X/?igshid=t57xdswc04l9

[fluxsci]

Elemental Flow - The Orbital Primer pt. 2 (5)

This is it! We have finally reached the conclusion of the orbital arc...or at least the second to last lesson. I’m sure it felt like the Frieza Saga, but I believe that I managed to explain the entirety of orbitals in a concise, but accurate way. Of course, I’ll leave it to you to tell me how I can improve to make this a better story for you. Because, like electrons, we all have to work together here.

In any event, let’s march on and be done with these orbitals. Ah…I can already hear the cheers from the Chemistry 101 students reading this.

Be sure to check out Part 4 for this one. You can’t understand where this one begins without seeing where the other one ends (hence ‘pt. 2’).

Now, it is time to explain the last quantum number.

Spin Quantum Number (s)

Electrons are trying to get rid of their energy in any way possible. Orienting themselves in a way that lowers energy is a good starting point, but they still have plenty of internal energy. In fact, electrons have their own, internal angular momentum, separate from the orbital angular momentum (l).

This was determined after a 1922 experiment by German physicists Otto Stern and Walther Gerlach. The aptly named Stern-Gerlach Experiment involved firing a beam of silver atoms* through a inhomogenous, or uneven, magnetic dipole and observing the results on a detecting wall at the end. The result, surprisingly, was that the beam was deflected in only two directions, landing flush against the wall in two bands.

But how could that be? There’s no way that there should be two, specific places in which the atoms ended up.  

If you think about it, if you threw twenty bar magnets past two huge magnets and looked at where they ended up, they would all be stuck on the wall in random places. After all, you have no idea what direction those magnets were when you threw them or how much attraction or repulsion one magnet had than another one, so you should have no idea exactly how they will come out. Shouldn’t it have been the same for these atoms?

In order to explain the significance of this inconsistency, I’ll need to diverge for a second into the physical quantity of momentum.

Gaining Momentum

Given that we know, from classical linear momentum calculation that there must a velocity, some speed over some time from some position which is usually produced by some force (say that ten times fast), and a mass, or the amount of matter an object has. This tells you how much, in numerical form, an object moves. In fact, you likely already knew the definition of “momentum” without knowing how to put it in words. Classical angular momentum is almost completely the same. The only difference is that an axis is involved, around which your mass rotates.

Thus, the two relative quantities are the moment of inertia and angular velocity. The latter is simply the rate at which rotation occurs. On the other hand, the moment of inertia, also known as the angular mass, is used to depict how much torque, or rotational force, you need to move an object a certain distance around an axis with respect to a certain position. The classic example of this is the tightrope walker.

If it was super easy to cause the one walking on a tightrope to flip around the rope (if gravity didn’t exist), then you would say that their moment of inertia is low. But when one walks across a rope you usually see them stick their arms out or hold a long rod. That single act increases the moment of inertia because you have changed the center of the mass, where the force acts. That is, more rotational force would be needed to rotate the walker. Now, Matthew, why did you go through the effort of explaining momentum here? Patience, viewer! The science will wrap together in a nice ribbon. Just in time for Christmas.

Magnets Start Small

I mentioned, from the now legendary Part 2, that electrons, as charged particles, can generate a magnetic field just by moving. It so happens that we know that electrons are “orbiting” the nucleus, and therefore, they must be exhibiting some sort of magnetic field as it is repeatedly revolving in this closed loop. But we never talked about what that field is doing. It wouldn’t make sense for the magnetic field to just disregard the electron and there is definitely no reason for the electron to not feel the force of the magnetic field.

Image via SchoolPhysics

By the way, if you orient your right-hand’s four fingers so that they are going along the path of the electron and then point out your thumb, that gives you the direction of the magnetic field. Every time. It’s called the Right-Hand Rule.

What would happen if you were to hold your hand on a ball lying on a table and then push your hand forward? The ball would roll in the direction your hand moves. It’s the same with electrons – they experience a rotational force, torque, from the magnetic field. The rotating electron creates another effect, according to electrodynamics. It now becomes a natural magnetic dipole, which is an object that generate magnetic fields that experience torque in such magnetic fields due to the presence of two opposite poles. In many ways, their magnetic effects are just tiny bar magnets. Electrons, too, have a “north” and “south” pole, or, more specifically, two poles at which their magnetic fields are strongest.

Image via Live Science

This is a dipole. You’ve seen bar magnets before.

 So, let’s do a roundup of what we just learned.

 Electrons generate magnetic fields which creates torque on them causing them to rotate and become similar to bar magnets. You should already recognize, then, where the concept of an electron’s angular momentum comes from. Indeed, electrons exhibit their own magnetic moment, from the rotational force, and, coupled with their motion, must create angular momentum!

 This is the origin of the theoretical “spin” that electrons have. Although we, realistically, don’t know if the electrons are spinning or not, this is just a name we give conventionally. You will learn why our convention fails us, especially when it comes to quantum mechanics, later.

 But, I digress. With all of that said…how did the electrons only end up in two places in the Stern-Gerlach Experiment?

 A Discrete Solution

 Stern and Gerlach were smart men. They knew, from Bohr’s prior experimentation of the electron, that it must be quantized. So when they crafted this experiment, they expected a quantized result. That is exactly what they saw. But just because they were correct in their hypothesis doesn’t mean their foundation was solid – a lesson for all of you upcoming scientists.

Image by Bill Watterson

Although that’s a result that you could hypothesize based on an expectation gained after seeing the ice in a glass of water melt, the foundation is all wrong.

The quantum mechanical theory of the time wasn’t correct. Their conclusion that the result was due to the quantization of the electron was not the reason for the quantized result.

 It was because of the electron’s angular momentum was directed in two specific direction. We call these half-spins, since one beam was split evenly into two. Basically, the momentum on the electrons directed the beam either upward or downward according to the direction of their rotational moment.

 A side-note: all elementary particles that hold these spins equal to ½ are called fermions, whereas if their spin value was 1 (what the value would be if the one beam went straight through without any division), it would be called a boson, a word you’ve likely heard before if you’re into physics. These are the two categories in which all particles in the universe reside.

 A Return To Form

 So...how about another summary?

 The Principle Quantum Number (n) determines the energy level, and thus, the electron’s shell. It is conventionally shown with a number from 1 to 5. The Orbital Quantum Number (l) determines where the electrons are with respect to the nucleus. It shows the sub-shell and is typically denoted with a letter (s, p, d or f) according to its number (0, 1, 2 and 3). The Magnetic Quantum Number (m) tells how many subshells there are. It is determined by looking at the subshell and taking the range from -l to l. Lastly, the complex Spin Quantum Number (s) determines whether the electron’s “spin” is +1/2 or -1/2.

 Lastly, there’s the Pauli Exclusion Principle, watching over these Quantum Numbers to make sure they behave themselves. No two electrons can have the same quantum mechanical state within the same atom. It was the aforementioned spin quantum number that proved this; remember that the electrons in the Stern-Gerlach did not simply mix – there was a distinction between +1/2 and -1/2. Furthermore, given that the Principle only works with differing quantum mechanical states, only fermions follow this Principle.

Image via futurespaceprogram

 This opens up a very important piece of orbital theory.

 That spin quantum number shows a great deal, indeed, folks. Because that Pauli Exclusion Principle makes it so that each subshell can only have two electrons – one with the positive spin and one with the negative spin.

 And that, my friends, will guide you into the Aufbau Principle…which we will discuss next time.

 The next lesson will end the Orbital Arc...I hope you’re ready. Because afterward, things will really pick up.

 Please ask questions if you are lost somewhere in these five parts. And share amongst all of your friends – not just the ones interested in science. We can all learn. We just need to light the fire.

*If you understood everything up to this point, you might be able to reason why silver atoms were used. I want to ask you why and give you these three hints to help you: 1) Use the periodic table 2) Orbital Quantum Number 3) Electrons and Protons

[fluxsci]

Elemental Flow - The Orbital Primer pt. 1 (4)

Image by Randall Munroe via xkcd

|| by matthew

This comic gave me a good laugh, despite not being directly related to quantum mechanical orbitals...

In any event, we are back again! I know how much you were looking forward (or perhaps dreading) this part. Well, if not looking forward to, perhaps still trying to reason how all of this is going on within every element in your body and facing a slight existential crisis. All I have to say, in that case, is to try not to worry about it, and, of course, prepare for another dive into the boundary of quantum mechanics and chemistry.

I, again, recommend that you check out the previous parts of the Elemental Flow series, especially Part 2. Familiarizing yourself with the quantum mechanics of electrons before this lesson will make this a smooth experience.

Quantum Numbers

What do the letters “s”, “p”, “d”, “f”, Aufbau, spin, and shapes have in common?

You might be scratching your head and wondering, “Why is he asking me this when I know he’s going to tell me.” And you’re right.  Let’s break out our handy dandy…periodic table. And notebook, if you have one (I got you, 90s kids).

Image via Science Notes

Orbitals are organized according to their energy levels. Naturally, every element on the periodic table must exist at a separate energy state in nature than each other (otherwise, what you learned in Part 1 and Part 2 would be meaningless – electrons have no need to configure themselves in different ways if every atom exists at the same energy level). Therefore, there must be a different orbital for each element. And, indeed, there is. The periodic table shows that, at the bottom of each element, there is a different electron configuration for each element. This exclusivity in configuration is called the Pauli Exclusion Principle.

Attentive readers might have already noticed the letters at the bottom of the elements on the periodic table – “s”, “p”, “d”, and “f”.

These labels are only descriptors of one of four quantum numbers. 

If you are lamenting the word “quantum” after Part 2 of the Elemental Flow series, don’t fret. A quantum number is a quantity within a quantum mechanical system. Since electrons are quantum mechanical systems, they hold specific quantities. That’s all.

Electrons have four such quantities. We call them the principal quantum number, or n, the orbital quantum number, or l, the magnetic quantum number, or m, and the spin quantum number, or s.

The Quantum Dive – Breaking the Shells

1) Principal Quantum Number (n)

The first, n, is the number that labels the energy level of an electron. Since we know, from Part 1, that the electrons with the lowest energy are the ones closest to the nucleus, we can tell that the lower the value of n, the lower the energy level. In chemistry, the energy level of an electron is described as its electron shell.

These shells are labeled from K to O starting from their innermost shell to their outermost shell, according to their principal quantum number. To be clear, an n of 1 is referred to as the K shell, n = 2 is L, n = 3 is M, n = 4 is N and n = 5 is O. While they do have this alphabetical label, when describing shells, more people recognize the numeric value of n. However, they can help you organize when we talk about the subsequent quantum numbers.

2) Orbital Quantum Number (l)

Next up, l. This quantum number tells about the orbital’s angular momentum, or the momentum brought about by rotation of electrons around some center – the nucleus.

Before I move on from here, I did want to explain this number more carefully.

For those familiar with astronomy, this quantum number is also called the azimuthal quantum number, as an azimuth is a certain angular measurement within a sphere.

Image via UOregon

Within our three-dimensional world, we can describe the position of anything in relation to anything else. As you can see, the azimuth and altitude give the direction of a star in this spherical system. North is usually used as the starting point for an angular calculation when comparing the horizontal position of a star and the altitude is given as angle from the observer in the center to the position on the sphere that the star is located.

But how does this relate to an electron? Take a look at this:

Image by tonfilm via vvvv

The observer is the nucleus, or, in this image, where the x, y, and z axes (representing each of our three dimensions) connect. The star is the point P, or the electron, with some x, y, and z coordinate. The angle between north, or the x-axis, and the point is defined as the azimuth. Lastly, the altitude angle would be the angle between the z-axis and the position of the point.

If the electron was just a point, or particle, then this would be a simple case of calculating the ordinary angular momentum.

But it isn’t just a particle, is it?

Image by Yuta Aoki via Wikimedia

The wave nature of electrons.

The angular momentum is harder to calculate in this system than it is in ordinary physics, due to the Wave-Particle Duality of the electron (discussed in Part 2). The electron is traveling quickly on a wave-like pattern. At any given time, we are unsure of where the electron may be. Instead of treating the electron like a particle, it is treated like a standing wave. More simply put, its wave functionality, constant and uninterrupted as it is, is used to determine its angular momentum. Therefore, the orbital angular momentum, is calculated completely differently than the classical angular momentum, which will be discussed when we reach the spin quantum number.

Perhaps the actual mathematics can be shown in a separate lesson if the interest is great enough? For now, recognize that, by solving this equation for the angular momentum, you receive non-negative integer values, or 0, 1, 2, 3, etc.

Aha! A new possibility reveals itself. If you were to believe that electrons were like their classical systems, you would probably say that it’s impossible for an object that’s moving to have 0 momentum. After all, if you’re walking down the street, you have momentum; how could an electron which is constantly revolving around the nucleus have 0 momentum? But quantum mechanically, a system with 0 angular momentum or, in other words, l = 0, simply orbits the nucleus in its wave-like pattern along the xy plane without any z altitude. The electron only has an azimuth, no altitude.

When I said in the last part that you had already learned about orbitals, this is what I meant. Because an electron orbiting the nucleus on an xy plane looks oddly familiar…

Image via Wikispaces

The Bohr Model of Hydrogen

Is that...? Why, yes it is! The Bohr Model! He did come up with the initial idea of orbitals. was that dastardly scientist was right!?

Not so fast.

First, let’s clean up this image. Since we’re not concerned with the electron’s decrease in energy state (like we were in part 2 when this was being explained), let’s look at the hydrogen atom at its lowest energy state.

Image via Chemistry LibreTexts

The electron is still on the n = 1 orbital and orbiting the nucleus like above. Only the n = 2 and n = 3 orbitals have been removed.

Bohr was only correct when it comes to things with one electron and an angular momentum of 0. This is because Bohr’s elementary model only observes the energy between the nucleus and the electrons only, not the energy created between the repulsion of electrons. The image above shows the only case in which the Bohr model is correct - with the hydrogen atom. Hydrogen only has one electron and its nucleus, meaning this fits Bohr’s model. Furthermore, as per the aforementioned Pauli Exclusion Principle, there are no other elements like hydrogen in nature.

To wrap up the second and most complicated quantum number, we make note of the fact that we can’t really know what the xy-axis is as it electrons see it.

To conceptualize what I’m saying, think of the image above as the wheels on a gyroscope.

Of course, in a quantum mechanical system, there is more discrete and fast motion, but this is a fantastic example. Now, if the revolving electron in the Bohr model was taking any of the wheels in the above gyroscope, you can understand why it would be hard to tell exactly where the electron would be, let alone where its x and y axes are.

But what you do know is that the electron is somewhere within the sphere made by the rotating gyroscope wheels.

This might sound familiar to you who remember or re-read Part 2 because this is the exact conclusion you derive from the Electron Cloud model that  Schrodinger developed!

Image via Ask A Mathemtician/Physicist

I love it when science comes together...You gotta admit, that’s pretty cool.

With all of that said, the purpose of the orbital quantum number is to tell you the shape of the electron subshell. Like the principal quantum number, these have an alphabetical naming system too…and it’s one you’ve already seen! That is: s, p, d and f. l = 0 to l = 3 represents s to f. Unlike the principal quantum number, however, it is conventional to use s, p, d and f rather than the numeric orbital quantum number value.

With that said, if the principal quantum number, n, is equal to 1 and the orbital quantum number, l, is equal to 0, you have a 1s system, which is the electron configuration of the hydrogen atom (check the bottom of the hydrogen element on your periodic table).

Now, I think after all of that, it’s good to keep ourselves organized.

To recap, the principal atomic number tells us the electron shell or energy level of the element, and the orbital quantum number tells us the electron subshell. There can be multiple subshells in one shell. And each individual electron configuration is called an orbital.

Image by thomji via Chemistry Stack Exchange

3) Magnetic Quantum Number (m)

Before we wrap up with this image, there’s something important in it that will help you understand the magnetic quantum number. 

You might have noticed above that there are three different p orbitals in the above image. That is due to the different ways an orbital can orient itself within space as the amount of electrons in the system increases. This is what Bohr did not account for in his model; when more electrons enter the system, in order to keep energy as low as possible, the system must orient itself differently within the three dimensions.

The magnetic quantum number is a handy way of telling us how many ways a subshell can orient itself. I say it’s handy because there’s a simple equation to tell you how.

For every value of l, there is a range of values of m from -l to l, including zero.

So, if our system is a d orbital, which is l = 2, there would be 5 ways the subshells could orient themselves, given by the m values -2, -1, 0, 1 and 2.

That’s all there is to that. See? Not so bad.

Intermission

Okay, okay. Break time. We don’t want to overcook your brains with chemistry and quantum theory. Fortunately, what we are going over is, theoretically, all there is to orbitals (without the droll mathematics, of course). And, as you already know, this leads to some amazing science. After all, after learning about electron shells, the next step can only be how elements combine to reduce energy even further!

Are you enjoying learning about how these microscopic particles work and seeing how something so complex can create something as simple as a drop of water and/or something as ubiquitous as air?

Let me know. I would love to talk science with you guys.

As always, thank you for joining me, and I will see you again very soon.

[fluxsci]

Elemental Flow - Valentia Orbitalis (3)

Image via MicroMountain

And we’re back with some more. This time, finally, we discuss orbitals. What if I told you that you already know what they are? For those of you who have already studied chemistry, you’ve possibly already started to put together the pieces from the last two lessons. For the rest of you, we have laid the groundwork for orbitals already by discussing what they are in detail. Orbitals are nothing more than the position of electron in the space of an atom. 

I should stop before I get ahead of myself. Because it’s been so long since we’ve talked about electrons, I think it’s only proper to begin with a summary of the past lessons. Of course, if you want to understand these at a higher level, please check out part 1 and part 2.

In the Name of Energy

Low energy means no problems. The first lesson on electrons focused on their orientation and how they exist in a way that decreases their energy. The second furthered that discussion, showing that microscopic particles exhibit both particle-like behavior and wave-like behavior, changing the number of possible places that electrons can exist within the three dimensions, again, to minimize energy. In both lessons, we have discussed that modeling exactly where the electron is is difficult, but telling where it might be in a “cloud” of possible positions is far easier.

I don’t exaggerate when I say that, if you understand those two things, you understand most of orbital theory. But, of course, I’ll show you what I mean.

Elementary Table

 First, we should establish a familiarity with the periodic table.

Image via Science Notes

Don’t be scared. Take a deep breath. This massive organization of scientific data should not scare you.

This table, like most periodic tables should, gives us all of the information required to talk about the elements. The key given explains what is within each box. To further explain, the number in the top left, or the atomic number, represents the number of protons within the atom. Given no excess in positive or negative charge, the atomic number can also be taken to refer to the number of electrons within an atom as well. The number in the top right, or the atomic mass or weight, is given as the size of an atom. Since the nucleus of any atom makes up most of the weight, you will usually see a reference to the mass number given before any particle. The mass number, unlike the atomic number, is the combined amount of protons and neutrons in any element.

 Image via IPod Physics

Elements will always have the same amount of protons, which is why the atomic number is defined as the number of protons. However, an element will not always have the same number of electrons or the same number of neutrons.

You might have heard the term “isotope” before. Isotopes are the variations of an elements, given by differing numbers of neutrons. Some isotopes are less stable than others and, the less stable they are, the less likely that they are occur less in nature.

Image via TutorCircle

As you can see, protium, the hydrogen with one proton only, is the most commonly occurring, and, as such, the mass number of hydrogen is usually written as 1. Isotopes of hydrogen can have a mass number of 2 or 3.

But now we get to the interesting and most relevant part of the table: the electron shells and configurations shown at the bottom.

Sharing Shells

Remember when I said in the first lesson that reactions between elements exist in a give-and-take relationship? It’s finally time to tie the neat bow on the present that I had been preparing for you since the beginning. Let’s jump right in.

 It is the electron shell that determines how many electrons an atom gives up. The theory of electron shells came from the idea that Niels Bohr had about electrons needing to be a certain distance away from the nucleus.

 The outermost electron shell is called the valence shell. This is the shell that interacts with the valence shells of other elements. We have determined that the preferred number of valence electrons for any element in the valence shell is eight. This is according to the amount of electrons within elements in the noble gas category (the elements on the rightmost column of the periodic table). The reason for that is due to a unique characteristic of noble gases – they are almost completely nonreactive. If you put a noble gas next to any element, without any further additions, nothing would happen.

 While the outermost shell is important, however, I would like to turn your attention to the inner shells – where the orbitals truly shine…in the next lesson. Don’t be too upset with me. You’ll appreciate this given the amount there is to tell you. Keep that periodic table handy.

 And feel free to review and ask questions in preparation for the next lesson.

[fluxsci]

The Elemental Flow Summary

The Elemental Flow Summary #Flux #Science #Atoms #Orbitals

Image via Vivax Solutions The Elemental Flow arc is long past us, but our objective is to make sure you understand what you’ve learned…It’s one thing to say that you’ve been taught. It’s another to say that you can remember – a general flaw brought about by time constraints in school. The Motivations for Electrons Electrons behave in a simple manner. There is only one factor that motivates it –…

[fluxsci]

Elemental Flow - The Aufbau Ribbon (6)

The modern masters promise very little; they know that metals cannot be transmuted, and that the elixir of life is a chimera. But these philosophers, whose hands seem only made to dabble in dirt, and their eyes to pore over the microscope or crucible, have indeed performed miracles. They penetrate into the recesses of nature, and show how she works in her hiding places. They ascend into the heavens: they have discovered how the blood circulates, and the nature of the air we breathe. They have acquired new and almost unlimited powers; they can command the thunders of heaven, mimic the earthquake, and even mock the invisible world with its own shadows.

- Mary Shelley (Frankenstein)

Did you notice that the scale of what we discuss is getting bigger? Yet there’s always going to be a ribbon to tie things up with…That’s the beauty of science having its gentle fingers on every pulse.

The ribbon around everything that we’ve discussed in the last 5 chapters is the Aufbau Principle. It basically describes the order of how electrons organize according to everything that we’ve learned. Specifically, electrons seek stability according to the rules of the Pauli Principle, which states that there can only be two electrons in any one orbital.

In addition, the Aufbau principle, from the German word “build-up” states that electrons must occupy the orbitals of the lowest energy before going to the higher energy orbitals.

That makes sense, right? Electrons have no need nor desire to be at a high energy level; if they can exist in a lower energy state, they will be.

The Build-Up

Before we begin, you might want to keep a periodic table handy.

Image via ScienceNotes

Building from chapter 4 and 5, the organization of each orbital conventionally takes the form of Principle-Orbital-Spin (n-l-s). The Aufbau Principle dictates that we start from lowest to highest energy level. As such, it’s surprisingly trivial to label these orbitals to see just how electrons organize themselves along the periodic table.

The first number, the Principle Quantum Number is what shows the energy level, and thus, the electron shell of an element. If we are trying to occupy the lowest energy states first, we start with 1 – ground state energy. Next, the Orbital Quantum Number, the subshell number. Its lowest value is 0, corresponding to its label - s. Last, the Spin Quantum Number gives you whether one or both electron spins have been filled. The two spins (negative and positive) of each subshell must be filled before moving to the next subshell.

The unnamed Magnetic Quantum Number, the subshell orientation number, is necessary for telling how a subshell is filled by electrons. As a reminder, telling how many orientations there are is as simple as looking at the orbital quantum number and counting the spectrum from negative to positive. For example, if the orbital number is 0, there’s only 1 subshell. If it’s 1, there are 3 (-1, 0, 1).

The n-l­-s system dictates that the lowest possible energy state is 1s1. This value is the numerical representation of an orbital. This particular orbital corresponds to hydrogen.

But remember, there are two electrons, spinning oppositely, per subshell. With the addition of the second electron, we hit 1s2. This state corresponds to helium.

Once all subshells’, and, therefore, the entire shell’s electrons have been filled, the next shell can be filled. We know that the next principle number, 2, marks an increase in energy states, which also means that the distance that electrons are from the nucleus increases. Ergo, the more energy electrons have, the more capacity they have to break away from the attractive forces of the nucleus.

With the increase in distance and the addition of even more electrons comes increases in possible electron configurations, resulting in not only new subshells, but also new orientations. Yet each orbital follows the Aufbau Principle. As such, you see an organization like the following picture.

Image via PrintableDiagram

This is an orbital diagram. Each arrow represents an electron and its spin.

Pretty easy, right? But, of course, science has to throw a proverbial wrench in our understanding. Why can’t it just be easy for once…? I know, dear reader, I know.

Attack of the Hund’s

When it comes to elements that have multiple orbitals orientations in a subshell, which is every element with a principle number of 2 or above, each orbital must have one electron spin occupied before it is occupied with the electron with the opposite spin. This is known as the Hund’s Rule. You could likely guess the reason for this now, but, just in case you haven’t understood the only motivation that electrons have yet, it is to reduce energy.

Two electrons grouping together in an orbital is already hard – the negative charges naturally repel each other. To reduce the effects of repulsion, the electrons inhabit the orbitals with similar energy levels first. Each spin direction has such a similar energy level to an electron with the same spin. That means, since Pauli’s Principle prevents two electrons with the same spin from existing in the same subshell, each subshell will be filled with one spin direction before they are filled with the opposite spin.

A respectable analogy is something that you’ve likely experienced. Have you ever been reading a book at a library or bookstore with plenty of empty chairs dispersed around? How would you feel if, then, someone sits right next to you, occupying your space? Doesn’t that just feel wrong? Maybe a little inconvenient? How about if someone sat directly across from you. Now that would just be awkward; imagine you looking up from your riveting novel only to see a pair of peering eyes looking back at you. But, if all of the seats in the socially appropriate places are taken, then there’s less of an issue with people taking the remaining seats. That’s, essentially, how electrons feel. They want to fill the empty, most distant seats before filling in in the inconvenient seats.

Therefore, orbital diagrams will show that electrons fill each orientation with the same upward spin before filling each orientation with the opposite downward spin. The necessity of having similar spin is based off the observed principle that like spins repel less.

For clarity, here is another orbital diagram with 36 elements. Check out boron (B) to Neon (Ne) to understand Hund’s Rule.

Image via Meta-Synthesis

We will need this for the next part, so hold onto it.

Diagonal Rule

There’s one more curve ball that you should be aware of.

Electrons tend to fill orbitals in a unique, but organized way after the 2p subshell in most cases. When you get to the third principle number, you gain yet another subshell – the d subshell.

As we’ve said 1s1 is hydrogen and 1s2 is helium. With each element in the periodic table, the number of electrons within the system grows by one. But when you get to Argon (Ar) and move to Potassium (K), it goes from 3p to 4s. Why would we skip the 3d shell? After all, we went from 1s, to 2s-2p, then 3s-3p. Shouldn’t 3d come next?

There was a little factor that I purposely did not mention until this point. You can actually define the energy of orbitals by adding the principle quantum number and the orbital quantum number – n + ­l. This is called the Madelung Rule, which gives the order that orbitals are filled in. So, if we take hydrogen, for example, with an n of 1 and an l of 0, or s, we see that it has an energy level of 1, which is the lowest. Hydrogen and helium, technically, both fit into this 1s category, but we know that helium has two electrons, while hydrogen has only one. Therefore, helium has more energy in the system.

To belabor the point, it would be as if you had a solitary magnet on the table. It won’t move on its own until you put something of a similar pole near it, in which case it will move away. Electrons experience a similar reaction to each other, and therefore, the element itself is more energetic the more electrons there are.

But, returning to potassium (K), which has an n of 4 and an l of 0, it has an energy level lower than Scandium (Sc), which has an n of 3 and an l of 2. Potassium, which occupies the 4s orbital, has an energy level of 4, while scandium has an energy level of 5. Therefore, the 4s level is filled first.

This staggering creates a well-known diagonal. In fact, we can easily tell how to fill orbitals by following this Diagonal Rule.

Image via HyperPhysics

It’s simply amazing how we manage to organize something as chaotic as an electron. I suppose, however, that this is how they organize; we are just observers in this game, of which we are a sentient and thinking part.

There’s one more amazing thing that these orbitals reveal about the periodic table. It explains the Noble Gases.

The Noble Story

Time for another callback. Remember in chapter 3, when I mentioned noble gases and valence electrons? I said that noble gases were almost completely nonreactive.

Look at this periodic table.

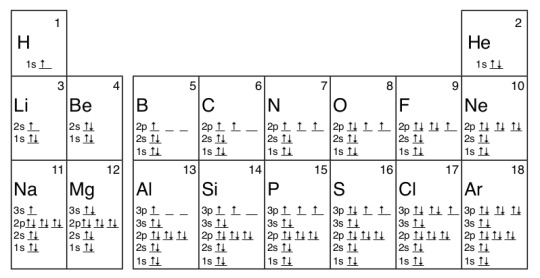
Image via Chemistry LibreTexts

This puts a little more attention on the electron configuration. Do me a favor: take a look at the noble gas group, or the column to the right.

Their orbitals are completely filled! There is not one spin arrow that is unaccompanied. You might have noticed that beryllium (Be) and magnesium (Mg) also fit this criterion. However, recall that every principle quantum number over 2 has a p or higher orbital. Those two elements, and all other elements in Group 2, don’t fill the p orbital, like neon and argon do in their respective rows.

Noble gases are nonreactive because there are no electrons required to complete their electron shells. Therefore, an element paired with a noble gas will lead to no result; there is no response to the phone call, as it were. Without space free for more electrons, there’s almost no way for elements to communicate. 

If you look at your complete periodic table and the image of the orbital diagram used in the Diagonal Rule section, you can see this is the case for Argon (Ar) and Krypton (Kr) as well. Yes, Superman is from a very noble planet indeed.

Conclusion

At last, the Elemental Flow Arc comes to its end. Now that you know what electrons are, in terms of how they move and organize themselves in an element, you are well equipped to understand how elements combine. In fact, I’ve already given you the answer to that. But, I suppose we will see soon, as we move with the flow eternal.