#terme spectroscopique

[unpeudephysique]

Termes spectroscopiques et micro-états

Nous nous sommes jusqu’à présent intéressé à l’état de plus basse énergie des atomes. Dans le cas du titane par exemple ([Ar] 4s2, 3d2) le terme spectroscopique de cet état de plus basse énergie est 3F2. La règle de Hund nous a aidé à déterminer ce terme spectroscopique :

Dans le monde incertain et changeant de la physique quantique, les électrons, pour peu qu’ils aient un peu d’énergie à revendre (thermique, électrique...) mais pas suffisamment pour sauter dans une sous-couche d’énergie supérieure, ne vont pas rester sagement dans les cases que nous leur avons assignées. Ils vont au contraire occuper tous les micro-états possibles de la sous-couche 3d2 compatibles avec le principe d’exclusion de Pauli.

Considérons le premier électron. Nous l’avons casé dans l’orbitale de nombre quantique ml = 2 mais il peut aussi bien occuper chacune des 4 autres orbitales de la sous-couche d et avoir le spin -1/2 ou +1/2, ce qui fait 10 possibilités. Supposons qu’il ait fixé son choix, il reste au second 9 choix possibles (le principe d’exclusion de Pauli empêche qu’il se trouve dans le même état que le premier). Cela nous fait 90 combinaisons en tout. Mais la distinction que nous avons faite entre 1er électron et 2ème électron est formelle : ils sont indiscernables. Il n���y a donc en fait que 45 micro-états différents possibles. Nous allons les lister.

Dénombrement des micro-états

Nous sommes dans une sous-couche d et il y a deux électrons, la projection du moment cinétique orbital L de l’atome sur l’axe de mesure peut donc prendre toutes les valeurs de -4 à +4 tandis que son spin peut prendre les valeurs -1, 0 et 1.

Remarque : mL et mS sont les valeurs que peuvent prendre les projections de L et S sur l’axe de mesure.

Les deux tableaux qui suivent détaillent toutes les configurations possibles respectant le principe d’exclusion de Pauli. Dans le premier sont répertoriées toutes les combinaisons avec mS = 1. Celles pour lesquelles mS = -1 donnent un tableau qui est l’exact symétrique de celui-ci.

Remarque : la première rangée ainsi que la dernière sont vides en raison du principe d’exclusion de Pauli.

Dans le deuxième tableau sont répertoriées toutes les configurations pour lesquelles mS est nul.

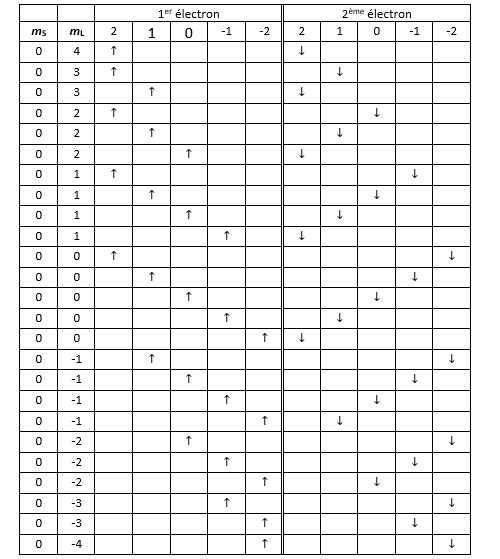
L’étape suivante consiste à faire la synthèse du nombre de micro-états pour chacun des couples (mL, mS). On retrouve bien les 45 micro-états prédits initialement.

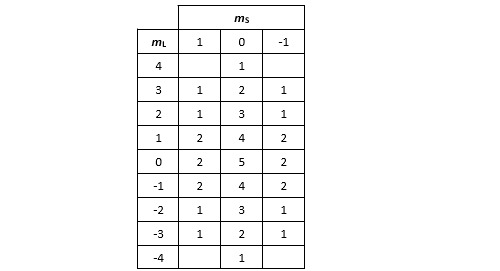
Nous allons rechercher maintenant les termes spectroscopiques principaux correspondant à ces différents micro-états. Considérons dans un premier temps les combinaisons présentant le terme mL le plus élevé. Ici il n’y en a qu’une et elle correspond au couple (mL=4, mS=0). Elle est caractéristique du terme spectroscopique 1G. Prenons maintenant un peu de recul. Si le titane possède un état tel que (L=4,S=0), il n’y a aucune raison que le moment cinétique orbital de cet état soit orienté uniquement dans l’axe choisi pour faire la mesure. Le terme spectroscopique 1G se décline donc également avec des valeurs de mL égales à 3, 2, 1, 0, -1, -2, -3, -4, ce qui nous fait 9 micro-états en tout. Puisque nous les avons identifier, nous pouvons les retirer du tableau. Pour cela, il suffit d’enlever 1 à tous les éléments de la colonne mS = 0.

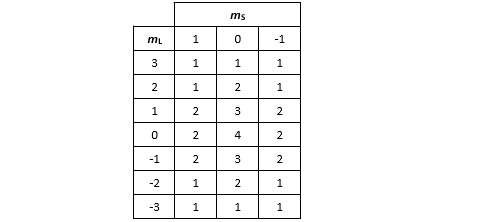
Poursuivons. Même démarche : recherchons les combinaisons présentant le terme mL le plus élevé. Cette fois il y en a trois : (3, 1), (3, 0) et (3, -1). On reconnait un état triplet dont le terme spectroscopique est 3F. Si on applique le même raisonnement que ci-dessus, il est clair qu’un état (L=3, S=1) peut apparaître sous la forme de plusieurs micro-états avec mL prenant toutes les valeurs entières possibles entre -3 et +3 et mS toutes les valeurs entières entre -1 et +1. Ceci nous fait 21 micro-états en tout. Pour les retirer du tableau il faut enlever 1 à toutes les cases.

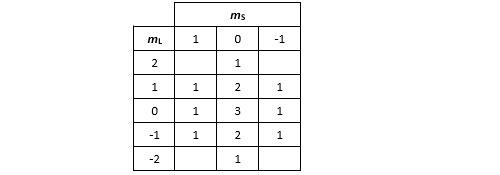
Si on poursuit la même démarche, on trouve le couple (2, 0) qui correspond au terme spectroscopique 1D, lequel regroupe avec 5 micro-états.

On aura compris le principe de ce dénombrement. Il nous donne également le terme spectroscopique 3P avec 9 micro-états et le terme spectroscopique 1S qui est singulet. On a donc au total 9 micro-états 1G, 21 micro-états 3F, 5 micro-états 1D, 9 micro-états 3P et un micro-état 1S. On constatera au passage que le micro-état (1, 0) par exemple peut très bien relever des états associée aux termes spectraux 1G, 3F, 1D ou 3P. Rien d’anormal dans tout cela. Cela signifie tout simplement que dans la « vraie vie », la fonction d’onde d’un atome dans ce micro-état est dans une superposition de ces 4 états !

Termes spectraux secondaires

Nous avons listé les termes spectraux principaux mais, pour être exhaustifs, il nous faudrait leur formulation complète : 2S+1LJ. Nous verrons dans un post ultérieur qu’elle joue un rôle essentiel dans certains phénomènes physiques comme l’effet Zeeman. Prenons par exemple le terme 3P. La valeur maximale de J pour cet état est J = L+S = 2. Le terme spectroscopique complet qui lui est associé est donc 3P2. Le nombre de micro-états auquel on peut attribuer ce terme spectroscopique est égal à 2J+1 = 5. Dans le cas du terme 3F, la valeur maximale de J est 4. Le terme spectroscopique complet qui lui est associé est donc 3F4 et il regroupe 9 micro-états.

Aïe... Cela ne nous fait en tout que 29 états. Il en manque donc 16. Si l’on se reporte aux décomptes faits plus haut, on voit d’ailleurs qu’on n’a pour le moment comptabilisé que 9 micro-états de type 3F alors qu’on en avait décompté 21 ! Idem pour 3P : on n’en a comptabilisé que 5 alors qu’on en attendait 9. Ceci résulte du fait que l’on n’a tenu compte que des micro-états tels que J = L+S. Or, rien n’oblique L et S à être orienté dans la même direction. Pour retrouver les micro-états manquants, il faut tenir compte aussi de ceux pour lesquels |L-S| < J < L+S.

Nous voilà rassurés : nous avons bien retrouvé nos 45 micro-états.

Energies associées aux termes spectroscopiques

Reste à déterminer l’échelle des énergies des micro-états associés à ces différents termes spectroscopiques. Les règles de Hund vont nous aider :

les termes spectroscopiques de plus grande multiplicité ont l’énergie la plus basse,

parmi ceux-ci, ceux qui ont le moment L le plus élevé ont l’énergie la plus basse,

enfin, pour un même couple (L,S), lorsque la sous-couche est moins qu’à moitié remplie, l’énergie décroît avec J alors que c’est le contraire lorsque la sous-couche est plus qu’à moitié remplie.

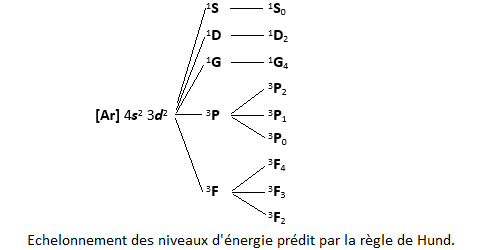
La réalité n’est pas toujours exactement conforme à la règle de Hund. L’écart entre les niveaux d’énergie est d’ailleurs souvent très faible, d’où des chevauchements. Seul le terme spectroscopique de l’état fondamental peut être prédit avec certitude. Ici, c’est 3F2.

Ordre de grandeur

Nous avons vu que l’ordre de grandeur du couplage spin orbite était donné par une formule simple :

Z étant le numéro atomique de l’atome considéré. Dans le cas du titane, Z = 22 et n = 3. L’écart d’énergie entre le micro-état 3P0 et le micro-état 3F2 est de 0,138 eV. Soit lambda la longueur d’onde correspondant à un tel écart :

Dans le cas considéré, elle vaut 9 microns, ce qui la situe dans l’infra-rouge.

Atome de Nickel

Le travail que nous avons fait est plutôt fastidieux... et il n’y a que 2 électrons dans la sous-couche 3d ! Que dire du nickel Ni qui en compte 8... Pas de panique. On va utiliser une astuce fort utile. Au lieu de comptabiliser les électrons on va s’intéresser aux « trous ». Pour être plus clair, au lieu de placer les électrons dans des cases vides, on va en retirer de cases pleines. Retirer un électron de spin +1/2 revient à ajouter un trou de spin -1/2. Retirer un électron de spin -1/2 revient à ajouter un trou de spin +1/2. Comme le moment cinétique L et le spin S d’une sous-couche pleine sont tous les deux nuls, on voit que le décompte dans le cas où on a deux trous conduit au même résultat que dans le cas où l’on a deux électrons... A une différence près : cette fois la sous-couche est plus qu’à moitié remplie. Le terme spectroscopique de l’état fondamental du nickel n’est pas 3F2 mais 3F4.

Termes spectroscopiques d’un état excité

L’exemple du titane partait de l’hypothèse que ses électrons de valence restaient dans la sous-couche 3d. Qu’ne est-il lorsqu’il est excité et que l’un de ses électrons saute dans une sous-couche d’énergie plus élevée ?

Prenons le cas du calcium [Ar] 4s2. Le terme spectroscopique de l’état fondamental est 1S0 (sous-couche 4s remplie). Dans le premier état excité l’un des électrons de valence passe dans la sous-couche 4p. L’électron 4s1 peut se trouver dans l’état (0,-1/2) et dans l’état (0,1/2). Pour l’électron 4p1 il y a plusieurs combinaisons puisque ml peut prendre les valeurs 1, 0, -1 et s les valeurs -1/2 et +1/2.

D’où l’on tire le dénombrement suivant :

Il est facile de voir que les termes spectroscopiques principaux sont 1P et 3P. Pour ce qui est des termes complets, le premier ne peut s’écrire que d’une seule façon : 1P1 et il couvre 3 micro-états. Quant au deuxième, la configuration 3P2 n’épuise pas tous les micro-états possibles (5 micro-états) et il faut lui adjoindre les configurations 3P1 (3 micro-états) et 3P0.

Quelles sont les transitions possibles ? Les transitions dL=1, dJ=1 mais pas les deux autres (une transition J=0 vers J=0 n’est pas possible même si dL=1).

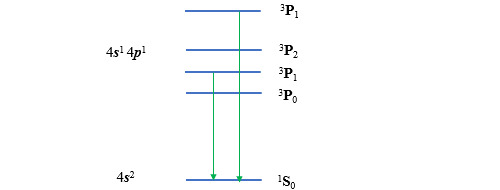
Revenons à l’atome de nickel. Le premier état excité de cet atome est l’état 4s1 3d9. Le dénombrement des micro-états ne pose aucune difficulté : l’électron de la sous-couche 4s ne peut se trouver que dans les états (0,-1/2) et (0,+1/2). Quant au trou de la sous-couche 3d9, il ne peut être que dans les états (l,-1/2) et (l,+1/2) avec l compris entre -2 et +2. On en déduit le tableau suivant.

On peut en extraire les termes spectroscopiques 3D3 et 1D2. Ces termes ne recouvrent que 12 micro-états sur 20. On vérifie facilement que tous les micro-états 1D ont été dénombrés (il y en a 5) mais pas tous les micro-états 3D (il devrait y en avoir 15). Il faut donc leur adjoindre les termes 3D2, 3D1.

Si on s’intéresse aux niveaux d’énergie de ces états excités par rapport aux niveaux associés à la configuration dite non excitée (4s2 3d8), on pourrait s’attendre à ce que les termes 3D aient un niveau supérieur à celui des niveaux 3F et inférieur à celui des niveaux 3P. En fait, il y a un entrelacement entre les niveaux 3F et les niveaux 3D.

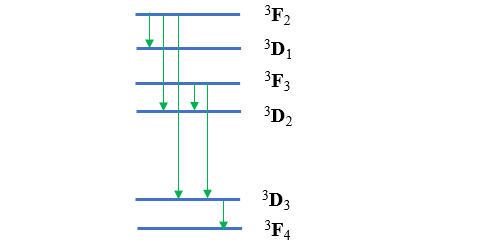
Les seules transitions possibles sont celles qui respectent les règles édictées plus haut :

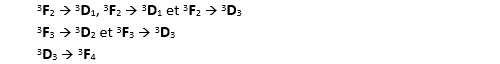
Les fréquences correspondant à ces sauts sont dans le domaine de l’infra-rouge.

Pour en savoir plus :

post sur la classification périodique des éléments

post sur le nuage électronique

post sur les nombres quantiques et les termes spectroscopiques

post sur l’effet Zeeman et l’expérience de Stern et Gerlach

post sur le spectre d’émission de l’hydrogène

post sur la raie à 21 cm de l’hydrogène

post sur les métaux de transition

post sur les métaux alcalins et alcalino-terreux

index

[reseau-actu]

Bien qu’il soit le plus connu des fermions élémentaires, l’électron n’a toutefois pas fini de révéler tous ses secrets aux scientifiques. Après avoir étudié ses propriétés physiques, longtemps les physiciens ont tenté d’identifier sa forme. Et récemment, grâce à une méthode impliquant des atomes artificiels, des chercheurs ont enfin réussi à déterminer la forme de l’électron. Un résultat essentiel qui pourrait ouvrir la voie au développement de futurs ordinateurs quantiques.

Des physiciens de l’Université de Bâle ont montré pour la première fois à quoi ressemble un électron dans un atome artificiel. Une méthode récemment développée leur permet de déterminer la probabilité qu’un électron soit présent dans un espace. Cela permet un meilleur contrôle des spins d’électrons, qui pourraient constituer la plus petite unité d’informations dans un futur ordinateur quantique. Les résultats des expériences ont été publiés dans la revue Physical Review Letters et la théorie correspondante dans la revue Physical Review B.

Le spin d’un électron est un bon candidat pour servir de bit quantique (qubit) au sein d’un ordinateur quantique. Contrôler et commuter ce spin ou le coupler avec d’autres est un défi sur lequel travaillent de nombreux groupes de recherche du monde entier. La stabilité d’un spin unique et l’intrication de différents spins dépendent, entre autres, de la géométrie des électrons, impossible auparavant à déterminer expérimentalement.

Des électrons évoluant au sein d’atomes artificiels

Les chercheurs des équipes dirigées par les professeurs Dominik Zumbühl et Daniel Loss du département de physique et du Swiss Nanoscience Institute de l’Université de Bâle ont mis au point une méthode leur permettant de déterminer spatialement la géométrie des électrons au sein de points quantiques.

Un point quantique est un piège de potentiel qui permet de confiner des électrons libres dans une zone environ 1000 fois plus grande qu’un atome naturel. Comme les électrons piégés se comportent de la même façon que les électrons liés à un atome, les points quantiques sont également appelés « atomes artificiels ». L’électron est maintenu dans le point quantique par des champs électriques. Cependant, il se déplace dans l’espace et, avec des probabilités différentes correspondant à une fonction d’onde, évolue dans des zones spécifiques dans son espace de confinement.

Graphiques montrant la géométrie spatiale des fonctions d’onde de l’électron en fonction des niveaux d’énergie. La détermination de cette géométrie permet aux chercheurs de caractériser la forme de l’électron. Crédits : Leon C. Camenzind et al. 2019

Les scientifiques utilisent des mesures spectroscopiques pour déterminer les niveaux d’énergie dans le point quantique et étudient le comportement de ces niveaux dans des champs magnétiques de force et d’orientation variables. Sur la base de leur modèle théorique, il est possible de déterminer la densité de probabilité de l’électron et donc sa fonction d’onde avec une précision à l’échelle nanométrique. « En termes simples, nous pouvons utiliser cette méthode pour montrer à quoi ressemble un électron pour la première fois » explique Loss.

Une meilleure compréhension des propriétés spatiales de l’électron

Les chercheurs, qui travaillent en étroite collaboration avec des collègues au Japon, en Slovaquie et aux États-Unis, ont ainsi une meilleure compréhension de la corrélation entre la géométrie des électrons et le spin de l’électron, qui devrait être stable le plus longtemps possible et rapidement commutable pour une utilisation en tant que qubit.

Un électron est piégé dans un point quantique formé dans un gaz bidimensionnel entre deux couches de semi-conducteur. Cependant, l’électron se déplace dans l’espace et, avec différentes probabilités correspondant à une fonction d’onde, reste à certains endroits dans son confinement (ellipses rouges). En utilisant les champs électriques, la géométrie de cette fonction d’onde peut être modifiée. Crédits : University of Basel

Sur le même sujet : La forme de l’électron à l’origine du déséquilibre matière-antimatière ?

« Nous pouvons non seulement cartographier la forme et l’orientation de l’électron, mais également contrôler la fonction d’onde en fonction de la configuration des champs électriques appliqués. Cela nous donne l’occasion d’optimiser le contrôle des spins de manière très ciblée » déclare Zumbühl.

L’orientation spatiale des électrons joue également un rôle dans l’intrication de plusieurs spins. De manière similaire à la liaison de deux atomes à une molécule, les fonctions d’onde de deux électrons doivent être placées sur un seul plan pour que l’intrication soit réussie. À l’aide de la méthode développée, de nombreuses études antérieures peuvent être mieux comprises et les performances des spin qubits pourront être encore optimisées à l’avenir.

Thomas Boisson 25 mai 2019 Physique1 Source: Trust My Science

[ca-se-passe-la-haut]

La matière noire rendue visible dans les amas de galaxies

Une nouvelle méthode vient de montrer tout son potentiel pour "éclairer" la matière noire à l'intérieur des amas de galaxie : il s'agit d'observer les étoiles errantes dans les amas de galaxies,  celles qui ont été éjectées lors de collisions galactiques et qui se retrouvent prises au piège du potentiel gravitationnel produit par la matière noire. Ces étoiles émettent une faible lumière qui est encore décelable par nos meilleurs télescopes. 

Cette faible luminosité visible à l'intérieur des amas entre leurs galaxies constitutives est appelée la lumière intra-amas (intracluster light, ICL). Pour montrer que la répartition des étoiles errantes produisant cette lumière correspondait bien à la répartition de la matière noire diffuse au sein des amas de galaxies, Mireia Montes (Yale university) et Ignacio Trujillo ont comparé des cartographies de la lumière intra-amas avec la distribution de masse déduite de mesures de lentilles gravitationnelles obtenues avec le télescope spatial Hubble (et son programme Frontier Fields). Ce programme s'est focalisé sur l'observation de 6 amas de galaxies avec une durée d'observation continue d'environ 100h pour chaque amas, permettant d'atteindre à la fois des objets très faiblement lumineux autour des amas de galaxies, des galaxies très lointaines amplifiées et déformées par lentille gravitationnelle, et la lumière très faible émanant de l'intérieur des amas de galaxies.

En superposant les deux types de cartographies, qui n'ont aucun lien (cartographie de masse et cartographie de lumière), les astrophysiciens obtiennent un accord quasi parfait : les étoiles errantes se retrouvent distribuées exactement là où se trouvent d'énormes quantité de masse invisible. 

Les chercheurs montrent dans leur étude publiée dans les Monthly Notices of the Royal Astronomical Society que à la fois les étoiles éjectées des galaxies errant au milieu des amas de galaxies et la matière noire diffuse autour de ces galaxies se comportent comme des composantes sans collision. En somme, la lumière intra-amas permet de littéralement "voir" où se trouve la matière noire. Cette méthode s'avère même plus efficace que la méthode classique de lentilles gravitationnelles car cette dernière requiert une étape de reconstruction délicate à mettre en oeuvre, associée à des mesures spectroscopiques longues à traiter. La méthode de Montes et Trujillo a juste besoin d'images profondes des amas de galaxies comme ce que peut faire le télescope Hubble, c'est à dire d'un peu de temps d'observation.

Au delà d'une cartographie inédite de la matière noire à l'intérieur des amas de galaxies, l'utilisation de l'ICL comme traceur introduit la possibilité, à terme, de tester la nature de la matière noire. Par exemple, si les particules de matière noire ont une caractéristique d'auto-interaction, cela devrait se traduire par une petite différence entre la distribution spatiale de la lumière et la distribution spatiale de la matière noire. Les premiers résultats de Montes et Trujillo ne permettent pas encore de déterminer si la matière noire se comporte de cette façon, mais tous les espoirs sont permis pour des futures observations. 

C'est dans ce cadre que Montes et Trujillo s'apprêtent à étudier plus d'amas de galaxies que les six qu'ils ont utilisés pour montrer la pertinence de leur méthode. Ils espèrent également beaucoup d'autres observations par d'autres équipes, sans compter l'utilisation du futur télescope spatial Webb qui devrait décupler la puissance de Hubble.

La matière noire dans les amas de galaxies est désormais visible.

Source

Intracluster light: a luminous tracer for dark matter in clusters of galaxies

Mireia Montes  Ignacio Trujillo

Monthly Notices of the Royal Astronomical Society, Volume 482, Issue 2 (11 January 2019) 

https://doi.org/10.1093/mnras/sty2858

Illustrations

1) L'amas de galaxies Abell S1063 imagé par Hubble (J. LOTZ/STSCL, ESA, NASA)

2) Etude de Abell S1063 par Montes et Trujillo : en bleu, le contour de la masse déduite des lentilles gravitationnelles et en vert le contour de la lumière intra-amas. Les deux contours coïncident. Le contour rouge correspond à l'émission de rayons X qui est décalée par rapport aux autres traceurs. (Montes, Trujillo/MNRAS)

via http://bit.ly/2PZFLAF

[designinthemoodforlife]

Parallaxe

La parallaxe est l’incidence du changement de position de l’observateur sur l’observation d’un objet. En d'autres termes, la parallaxe est l'effet du changement de position de l'observateur sur ce qu'il perçoit. Ce mot apparaît au xvi ème siècle, emprunté au grec παράλλαξις, qui signifie « déplacement contigu ; parallaxe ».

A. Incidence du changement de position de l'observateur sur l'observation d'un objet. 1. MÉTROL. Erreur de parallaxe ou p.ell., parallaxe. ,,Angle pouvant exister entre la direction du regard d'un observateur et la perpendiculaire à une graduation amenant une lecture inexacte de la mesure faite`` (DEW. Mes. 1973). Dans les instruments de mesure on supprime pratiquement l'erreur de parallaxe en se plaçant de manière à voir dans le même plan l'aiguille ou l'index et l'image qu'en donne un miroir situé dans le plan du cadran ou de l'échelle (LAITIER 1969). 2. PHOT. Parallaxe de visée. ,,Différences de cadrage entre l'image visée et l'image enregistrée`` (Microgr. 1980). 3. PHYSIOL. Parallaxe oculaire. ,,Angle formé par les axes visuels d'une personne qui fixe un point quelconque d'un objet`` (PAUL Télédétection 1982). Parallaxe binoculaire ou stéréoscopique. ,,Différence apparente dans la position d'un objet lorsqu'il est regardé par l'un ou l'autre oeil séparément, la position de la tête de l'observateur demeurant la même`` (Méd. Biol.t.3 1972).  P. métaph. Ce sont des «Z'amis utiles», comme dit Mariette appuyant sur la liaison. Utiles à quoi, on ne sait pas. À nous faire croire qu'ils peuvent l'être. À nous entourer de semblables. À nous montrer que tout est binaire, deux par deux, comme les yeux, qui n'ont pourtant qu'un regard. À nous apprendre que ce regard doit laisser beaucoup de paupière. Car on en voit des choses en faisant avec eux bouger la parallaxe! (H. BAZIN, Le Matrimoine, Paris, éd. du Seuil, 1967, p.77). 4. TOPOGR. [En vision stéréoscopique] Différence de coordonnées. Parallaxe transversale ou de hauteur ou verticale. Différence d'ordonnées entre deux points. Parallaxe longitudinale ou horizontale ou linéaire. Différence d'abscisse entre deux points (d'apr. Topogr. 1980 et PAUL Télédétection 1982). B. Angle sous lequel on voit perpendiculairement depuis un point donné, un objet donné. 1. ASTRON. [L'objet est une unité de longueur de référence] a) [L'astre considéré appartient au système solaire, l'unité de longueur de référence est le rayon terrestre] Parallaxe diurne ou horizontale ou p.ell., parallaxe. On donne le nom de parallaxe de la lune à l'angle sous lequel on voit de la lune le demi-diamètre de la terre (FLAMMARION, Astron. pop., 1880, p.114):

1. L'observateur terrestre entraîné par la rotation de notre globe se trouve (...), en fonction du temps, dans des positions variables par rapport à un astre extérieur. Cet effet est négligeable pour les étoiles, mais pas pour les objets comme la Lune. Pour ramener une observation au centre de la Terre, il faut donc la corriger de cette parallaxe dite «diurne» pour rappeler qu'elle réside dans la rotation du globe. MULLER 1980.

b) [L'astre considéré est extérieur au système solaire, l'unité de longueur de référence est l'unité astronomique] Parallaxe annuelle ou stellaire ou p.ell., parallaxe. La distance d'une étoile est définie par sa parallaxe, angle sous lequel on voit depuis l'étoile l'unité astronomique de longueur (qui est la valeur moyenne du rayon de l'orbite terrestre, soit 150000000 de km) (Hist. gén. sc., t.3, vol. 1, 1961, p.137). Parallaxe annuelle des étoiles. Un observateur terrestre T qui se déplace au cours de l'année autour du soleil S voit un astre immobile proche E (...) dans une direction qui varie avec la position de l'observateur (KOURGANOFF, Astron. fondam., 1961, p.67):

2. ... que dire de sa révolution [de la terre] autour du soleil. Ici encore, nous avons trois phénomènes qui pour le ptoléméien sont absolument indépendants et qui pour le copernicien sont rapportés à la même origine; ce sont les déplacements apparents des planètes sur la sphère céleste, l'aberration des étoiles fixes, la parallaxe de ces mêmes étoiles. H. POINCARÉ, Valeur sc., 1905, p.273.

 [Suivant le mode d'obtention de la mesure (par visée directe, dynamique, spectroscopique, photométrique, statistique)] Parallaxe trigonométrique, dynamique, spectroscopique, photométrique, statistique (d'apr. SCHATZMAN, Astrophys., 1963, p.38, 95, 97 et Astron. 1973). 2. TOPOGR. ,,Petit angle sous lequel est observée la longueur connue d'une stadia`` (Topogr. 1980). Prononc. et Orth.: []. Att. ds Ac. dep. 1694. Étymol. et Hist. 1557 (P. DE MESMES, Inst. astron., p.70 ds GDF. Compl.). Empr. au gr. «mouvement alternatif, astron.; parallaxe».

[unpeudephysique]

Spectre de l’hydrogène

La longueur d’onde des raies émises par l’atome d’hydrogène est prédite par une formule appelée formule de Rydberg :

Cette formule généralise une formule empirique établie par Johann Balmer en 18885 à partir des raies de l’hydrogène dans le domaine visible. Le fondement théorique de cette formule ne fut découvert que plus tard, grâce aux travaux de Niels Bohr. Il démontra que les raies spectrales d’un atome correspondaient à des sauts quantiques entre les différents états d’énergie possible de ses électrons. Ces états d’énergie sont quantifiés et l’équation de Schrödinger permet de les déterminer. Chacun de ces sauts se traduit par l’émission d’un photon dont la longueur d’onde est inversement proportionnelle au différentiel d’énergie :

Dans le cas d’un atome d’hydrogène, on peut simplifier l’équation de Schrödinger en l’appliquant à un électron évoluant dans un potentiel coulombien. Il est possible alors possible de la résoudre analytiquement. On montre que l’écart entre les différents niveaux d’énergie possibles correspondent bien aux valeurs prédites par la formule de Rydberg. En astronomie, on a donné un nom aux différentes séries de raies spectrales de l’atome d’hydrogène :

La formule de Rydberg s’applique aussi aux atomes hydrogénoïdes. Les atomes hydrogénoïdes sont des cations dépouillés de tous leurs électrons sauf 1 (Li2+, Be3+...). Dans ce cas :

Z étant le numéro atomique de l’atome considéré, M sa masse atomique et me la masse de l’électron.

Lorsque les atomes possèdent plus d’un électron dans leur bande de valence, la formule de Rydberg ne s’applique plus. Il faut tenir compte d’un phénomène appelé couplage spin-orbite (voir le post à ce sujet).

Pour en savoir plus :

post sur la classification périodique des éléments

post sur le nuage électronique

post sur les nombres quantiques et les termes spectroscopiques

post sur l’effet Zeeman et l’expérience de Stern et Gerlach

post sur la raie à 21 cm de l’hydrogène

index

[unpeudephysique]

La raie à 21 cm de l’hydrogène

Si vous vous intéressez à l’astronomie, vous ne pouvez pas ne pas avoir entendu parler de la raie à 21 cm de l’hydrogène. Cette raie d’émission de l’atome d’hydrogène est un marqueur de l’existence de nuages d’hydrogène à l’état atomique dans l’espace interstellaire. A quoi correspond-elle ?

L’atome d’hydrogène est composé d’un proton et d’un électron. L’électron occupe le niveau d’énergie 1s. Dans ce niveau, deux configurations sont possibles suivant que le spin de l’électron et celui du proton sont parallèles ou antiparallèles. Or la configuration antiparallèle correspond à un niveau d’énergie un peu plus faible. La différence est minime, moins d’un millionième d’eV. C’est cependant suffisant pour que les électrons qui passent de la configuration parallèle à la configuration antiparallèle émettent un photon dont la fréquence est de 1420,4 MHz, soit 21 cm de longueur d’onde. Cette transition est appelée transition hyperfine de l’hydrogène. 

Elle est caractéristique de l’hydrogène à l’état atomique. Lorsque l’hydrogène est à l’état moléculaire H2, le principe d’exclusion de Pauli impose en effet que les deux électrons que se partagent les deux atomes de molécule aient un spin différent, ce qui rend impossible la transition.

Pour en savoir plus :

post sur les nuages électroniques

post sur les nombres quantiques et les termes spectroscopiques

post sur le spectre d’émission de l’hydrogène

index

[ca-se-passe-la-haut]

Les derniers mois d'une étoile en fin de vie retracés en observant sa supernova très tôt après l'explosion

Que se passe-t-il juste avant qu'une étoile massive explose en supernova ? Une réponse à cette question épineuse vient d'être apportée grâce au suivi spectroscopique  très rapide de la suite de l'explosion d'une supernova apparue en 2013, qui a permis de retracer ce qui s'est passé dans les mois précédents.

SN 2013fs a été détectée le 6 octobre 2013 à l'Observatoire du Mont Palomar dans la galaxie NGC 7610 distante de 160 millions d'années-lumière. Dans les minutes qui ont suivi, plusieurs télescopes ont été braqués vers la supernova pour suivre l'évolution de sa luminosité et analyser sa lumière, notamment le télescope de l'observatoire de Las Cumbres, qui a continué à suivre la supernova sur plusieurs semaines. Après plus de trois ans de travail sur les données enregistrées, les résultats sont publiés aujourd'hui dans Nature Physics. Ils permettent de comprendre ce qui s'est passé quelques mois avant l'instant fatidique de l'explosion : l'étoile a perdu énormément de matière de son enveloppe.

L'étoile à l'origine de SN2013fs était une supergéante rouge d'une masse comprise entre 8 et 10 masses solaires et âgée de seulement quelques millions d'années, selon l'équipe menée par Ofer Yaron (Weizmann Institute of Science, Israel). Il n'est pas étonnant que ce type d'étoile produise une supernova par effondrement de cœur (une supernova de type II), mais ce qui a grandement surpris les chercheurs, c'est de constater qu'elle était entourée d'une dense coquille de gaz qui a été éjectée durant les derniers mois avant l'explosion, ce qui est totalement nouveau pour ce type d'étoile. La détermination de la présence de cette coquille de gaz a été obtenue par l'équipe internationale en observant une émission de fluorescence caractéristique. Le rayonnement de la supernova, en atteignant cette zone, a ionisé le gaz, les électrons se sont ensuite recombinés avec les atomes ionisés en émettant des photons de longueur d'onde spécifique, traçant par la même occasion la nature de la matière formant cette coquille ; de l'oxygène, de l'hélium, de l'azote, les éléments forgés par la fusion nucléaire dans l'étoile et composant ses couches externes.

Comme cette émission de fluorescence s'est éteinte environ 20 heures après le T0 de l'explosion, elle donne aux astrophysiciens une idée de la taille de la coquille de matière : 5 fois la distance Soleil-Neptune.

A partir de là, et en considérant que l'étoile ait pu éjecter une partie de son enveloppe à la vitesse de 100 km/s, les chercheurs évaluent que cette éjection aurait duré pendant les 500 jours précédant l'explosion.

Après l'intense rayonnement ionisant de la supernova est arrivée son onde de choc sur la coquille de gaz, ce violent mouvement destructeur de matière des couches internes de l'étoile en expansion à une vitesse de l'ordre de 10% de la vitesse de la lumière. L'équipe de Ofer Yaron montre que l'onde de choc a totalement dispersé la coquille de gaz en 5 jours, après l'avoir échauffé jusqu'à 60000°.

Les chercheurs estiment que la masse de la matière éjectée avant l'explosion représentait un millième de masse solaire. ce qui peut paraître peu mais est déjà supérieur à la masse de Jupiter et en tous cas bien supérieur à ce que les spécialistes s'attendraient à voir sur une telle supergéante rouge. 

Ces précieuses données vont fournir aux astrophysiciens de nouvelles idées sur cette phase de l'évolution stellaire, l'ultime, qui reste encore mal définie. En effet, les observations détaillées des supernovas ne débutaient le plus souvent que trop tard, après que l'explosion ait détruit les traces de son environnement proche. Cette mesure spectroscopique est la première a avoir été menée aussi tôt après l'explosion.

Un suivi détaillé très rapide après l'explosion est la clé pour reconstruire le passé immédiat de l'étoile en fin de vie. Grâce aux programmes d'observation systématiques actuels et futurs à la recherche d'événements transitoires, de plus en plus de supernovas vont pouvoir être suivies très tôt après leur découverte. On pourra certainement savoir bientôt si SN 2013fs est une exception ou non. Le Graal des astrophysiciens serait à terme de pouvoir détecter des supernovas avant qu'elles n'explosent, mais on n'en est pas encore là.

Référence

Confined dense circumstellar material surrounding a regular type II supernova

O. Yaron, et al.

Nature Physics (13 février 2017) 

http://ift.tt/2lPH8Hs

via http://ift.tt/2lXm4un