#satmathprep
Explore tagged Tumblr posts
Text

The SAT Math section assesses your mathematical skills, including your ability to work with numbers and expressions. Understanding how to analyze and calculate properties of two-digit numbers is essential for solving math problems on the SAT and in real-life scenarios. In this video, we will explore a SAT Math question that involves finding the sum of the digits in a two-digit number: "In a two-digit number, the units digit is x, and the tens digit is (x + 3). What is the sum of the digits in the number?" The correct answer is Option D) 11x + 30. By the end of this exploration, you will have a clear understanding of how to find the sum of digits in such numbers, improving your performance on the SAT Math section.
Question: Finding the Sum of Digits in a Two-Digit Number
Question: In a two-digit number, the units digit is x, and the tens digit is (x + 3). What is the sum of the digits in the number?
Options:
A) 11x + 3
B) 2x + 3
C) 3 + x
D) 11x + 30
Explanation and Key Concepts: When dealing with two-digit numbers, you can represent them as 10 times the tens digit plus the units digit. In this problem, the tens digit is (x + 3), and the units digit is 'x.' The sum of the digits is found by adding the tens and units digits, which leads to the expression 11x + 30.
Analyzing and calculating properties of two-digit numbers is an essential skill for the SAT Math section and beyond. This skill allows you to manipulate numbers and solve various mathematical problems efficiently. By mastering this skill, you'll not only excel on the SAT but also enhance your overall mathematical proficiency, which can be applied to various real-life scenarios.
#SATMathTips#AlgebraSimplification#MathExpression#SATMathPrep#MathematicsTutorial#SATMathProblems#TestPreparation#SATExamTips#MathSimplification#SATMathematics#SATTest#MathHelp#ProblemSolving#SATMathSkills#AlgebraicExpression#MathematicalEquivalence#SATStudy#MathExplained#SATPreparation#MathConcepts
0 notes
Photo

Join us for SAT prep classes and ace the test with flying colors! Our expert instructors will have you #y2academy and nailing those practice exams in no time. To know more, visit y2academy.com #SATprep #SATmath #SATtutor #SATtestprep #SATstudyguide #SATstudy #SATmathtutor #SATmathprep #SATmathstudy #SATmathtips #SATmathtricks #SATmathstrategies #SATmathskills #SATmathpractice #SATmathproblems #SATmathsuccess #testprep https://www.instagram.com/p/CnqhtffvW0E/?igshid=NGJjMDIxMWI=
#y2academy#satprep#satmath#sattutor#sattestprep#satstudyguide#satstudy#satmathtutor#satmathprep#satmathstudy#satmathtips#satmathtricks#satmathstrategies#satmathskills#satmathpractice#satmathproblems#satmathsuccess#testprep
0 notes
Text

The SAT Math section assesses your mathematical skills, including your ability to perform operations with algebraic expressions and identify their differences. Understanding how to find the difference between two expressions is essential not only for the SAT but also for various mathematical and real-life scenarios. In this video, we will explore a SAT Math question that involves finding the difference between two algebraic expressions: "What is the difference between (3a + 2b) and (-2a - 5b)?" The correct answer is Option A) 5a + 7b. By the end of this exploration, you will have a clear understanding of how to find the difference of algebraic expressions, enhancing your performance on the SAT Math section.
Question: Finding the Difference of Algebraic Expressions
Question: What is the difference between (3a + 2b) and (-2a - 5b)?
Options:
A) 5a + 7b
B) -5a - 7b
C) 5a - 7b
D) a - 3b
Correct Answer: Option A) 5a + 7b
Explanation and Key Concepts: Finding the difference between two algebraic expressions involves subtracting one expression from the other and then combining like terms. Remember that subtracting a negative expression is equivalent to adding the positive expression.
Understanding how to find the difference between algebraic expressions is a fundamental skill for the SAT Math section and beyond. This skill is applicable in various mathematical and real-world scenarios, allowing you to analyze differences and make informed decisions. By mastering this skill, you'll not only excel on the SAT but also enhance your overall mathematical proficiency.
#SATMathTips#AlgebraSimplification#MathExpression#SATMathPrep#MathematicsTutorial#SATMathProblems#TestPreparation#SATExamTips#MathSimplification#SATMathematics#SATTest#MathHelp#ProblemSolving#SATMathSkills#AlgebraicExpression#MathematicalEquivalence#SATStudy#MathExplained#SATPreparation#MathConcepts
0 notes
Text
SAT Math - How to find the value of x + y + z if x + y = 5, y + z = 7 and z + x = 12.
The SAT Math section assesses your ability to work with various mathematical concepts, including solving systems of linear equations. This skill is not only crucial for the SAT but also for real-world applications in fields like science, engineering, and economics. In this video, https://www.youtube.com/watch?v=34Cdnk9i_uo we will explore a SAT Math question that involves solving a system of three linear equations: "If x + y = 5, y + z = 7, and z + x = 12, what is the value of x + y + z?" The correct answer is Option A) 12. By the end of this exploration, you will have a clear understanding of how to solve systems of linear equations, enhancing your performance on the SAT Math section.
Question: Solving a System of Linear Equations
Question: If x + y = 5, y + z = 7, and z + x = 12, what is the value of x + y + z?
Options: A) 12 B) 2 C) 5 D) 24
Explanation and Key Concepts: Solving a system of linear equations involves finding values for the variables that satisfy all the equations simultaneously. In this case, we used the method of adding the equations together to eliminate one variable and isolate x + y + z. It's essential to perform the same operation (addition in this case) to all equations in the system to maintain equality.
Solving systems of linear equations is a fundamental skill in mathematics and has applications in various fields. Whether you encounter such problems on the SAT Math section or in real-life situations, the ability to find solutions to systems of equations is invaluable. By mastering this skill, you'll not only excel on the SAT but also be well-equipped for mathematical challenges in the future.
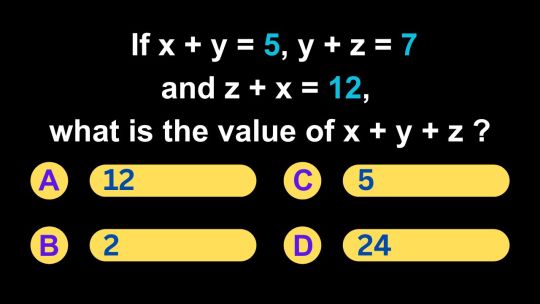
#SATMathTips#AlgebraSimplification#MathExpression#SATMathPrep#MathematicsTutorial#SATMathProblems#TestPreparation#SATExamTips#MathSimplification#SATMathematics#SATTest#MathHelp#ProblemSolving#SATMathSkills#AlgebraicExpression#MathematicalEquivalence#SATStudy#MathExplained#SATPreparation#MathConcepts
0 notes
Text

Welcome to another SAT math session! 📚 Today, we're diving deep into fractions comparison, a crucial skill for acing the SAT math section. We'll compare fractions step by step, and I'll walk you through solving questions like:
Comparing 5/8 and 7/12
Analyzing 5/9 and 11/15
Evaluating 11/12 and 15/16
The SAT Math section assesses your mathematical skills and ability to work with various concepts, including fractions. Comparing fractions is a fundamental skill, both for standardized tests like the SAT and for practical life situations. In this article, we will tackle a series of SAT Math questions that involve comparing fractions and determining their relationships. By the end of this exploration, you will have a firm grasp of comparing fractions and be better prepared to excel in this aspect of the SAT Math section.
Comparing fractions is a fundamental skill in mathematics, and it plays a crucial role in various mathematical concepts and real-life applications. Mastery of this skill is essential not only for the SAT Math section but also for everyday problem-solving. By understanding the techniques for comparing fractions, you can confidently tackle SAT Math questions that involve these concepts and strengthen your overall mathematical proficiency.
Whether you're a seasoned math enthusiast or preparing for the SAT, this video offers valuable insights and practice to boost your confidence.
Don't forget to hit the like button and subscribe for more SAT test prep tips, tricks, and strategies. Let's tackle fractions comparison together! 🚀
#shorts#satmathprep#satmath#satmaths#satmathtestprep#sattestprep#satpreparation#algebraicexpressions#mathproblemsolving#satmathpractice#YouCanLearnAnything#satmathreview#satmathtips#satmathwalkthrough#satmathtricks#satmathquestions#satmathpractice2023#satmathsection#satmathconcepts#satmathtipstricksandstrategies#satmathdigital#satmath2023
0 notes
Text
youtube

Welcome to another SAT math tutorial where we demystify the art of converting improper fractions into mixed fractions! This skill is indispensable for acing SAT math questions involving fractions, and we're here to make it simple.
Fractions are a fundamental concept in mathematics, representing parts of a whole or ratios between quantities. Understanding fractions is essential in various mathematical applications and daily life. One aspect of working with fractions is converting improper fractions to mixed fractions. In this article, we will explore the process of converting improper fractions into mixed fractions through a series of examples. By the end of this journey, you will be proficient in this mathematical transformation.
Now, let's explore the conversion process through examples.
Question 1: Convert 38/7 into a mixed fraction.
Question 2: Convert 47/15 into a mixed fraction.
Question 3: Convert 189/16 into a mixed fraction.
By the end of this video, you'll be well-equipped to convert improper fractions into mixed fractions confidently. Don't forget to like, subscribe, and hit the notification bell for more SAT math practice, tips, and strategies.
Join us in mastering SAT math and boosting your performance on test day! 🚀📚
#satmath#satmathpractice#satmaths#YouCanLearnAnything#satmathreview#satmathtips#satmathprep#satmathwalkthrough#satmathtricks#satmathquestions#satmathpractice2023#satmathsection#satmathconcepts#satmathtipstricksandstrategies#satmathdigital#satmath2023#shorts#satmathtestprep#sattestprep#fractions#mixedfractions#satpreparation#Youtube
0 notes
Text
youtube
Welcome to our SAT math practice session, where we're tackling the art of converting mixed fractions to improper fractions! If you've ever wondered how to master this skill for the SAT math section, you're in the right place.
Fractions are fundamental components of mathematics that represent parts of a whole or ratios between quantities. In many mathematical scenarios, it is necessary to convert mixed fractions (also known as mixed numbers) into improper fractions. This transformation simplifies calculations and facilitates comparisons. In this article, we will delve into the process of converting mixed fractions into improper fractions, using several examples to demonstrate the method. By the end of this journey, you will have a solid understanding of this essential mathematical skill.
Now, let's explore the process of converting mixed fractions to improper fractions through a series of examples.
Question 1: Convert 1³/₄ to an improper fraction.
Question 2: Convert 4⁵/₇ to an improper fraction.
Question 3: Convert 7⁹/₁₃ to an improper fraction.
Question 4: Convert 12⁶/₂₅ to an improper fraction.
By the end of this video, you'll have a solid grasp of this concept, allowing you to tackle similar SAT math questions confidently.
Don't forget to hit the like button, subscribe to our channel, and ring the notification bell for more SAT math practice, tips, and strategies. Join us in mastering SAT math and boosting your confidence on test day! 🚀📚
#shorts#satmathprep#satmath#satmaths#satmathtestprep#sattestprep#sattest#satpreparation#SATMath#AlgebraicExpression#MathProblemSolving#satmathpractice#YouCanLearnAnything#satmathreview#satmathtips#satmathwalkthrough#satmathtricks#satmathquestions#satmathpractice2023#satmathsection#satmathconcepts#satmathtipstricksandstrategies#satmathdigital#satmath2023#Youtube
0 notes
Text
youtube
Welcome to your comprehensive SAT math preparation session! In this video, we're diving deep into the world of rational numbers, equipping you with essential skills to tackle SAT math questions with confidence. Let's tackle seven challenging questions together: 𝐐𝐮𝐞𝐬𝐭𝐢𝐨𝐧 𝟏: Simplify (2/3) + (-4/5) + (7/15) + (-11/20) to its simplest form. Your options are (A) -1/5, (B) -13/60, (C) -4/15, (D) -7/30. 𝐐𝐮𝐞𝐬𝐭𝐢𝐨𝐧 𝟐: Find the value of (9/2) x (-4/3). Choose from options (A) 6, (B) -6, (C) 1, (D) none of these. 𝐐𝐮𝐞𝐬𝐭𝐢𝐨𝐧 𝟑: Calculate the value of (3/-5) x (-5/-3). You can choose from (A) -1, (B) 0, (C) 1, (D) none of these. 𝐐𝐮𝐞𝐬𝐭𝐢𝐨𝐧 𝟒: Determine the value of (3/10) x (-2/3). Your options include (A) 5, (B) 1/5, (C) -1/5, (D) none of these. 𝐐𝐮𝐞𝐬𝐭𝐢𝐨𝐧 𝟓: Find the value of (-6) ÷ (2/3). Will it be (A) -9, (B) 9, (C) -4, or (D) none of these? 𝐐𝐮𝐞𝐬𝐭𝐢𝐨𝐧 𝟔: Calculate (-1/8) ÷ (3/4). Is the answer (A) -1/6, (B) 1/6, (C) -3/32, or (D) none of these? 𝐐𝐮𝐞𝐬𝐭𝐢𝐨𝐧 𝟕: Solve the inequality (-5/7) □ (2/3) and choose from (A) greater than sign, (B) less than sign, (C) =, or (D) none of these. Our experienced instructor will guide you through these problems, providing clear and insightful solutions. Understanding rational numbers is fundamental for success in the SAT math section, and we're here to ensure you not only find the right answers but also grasp the underlying concepts. By the end of this video, you'll feel more confident and prepared to conquer SAT math challenges. Don't forget to hit the like button, subscribe to our channel, and ring the notification bell for more SAT math practice, tips, and strategies. Let's embark on this math journey together, gearing up for SAT success! 🚀📚
#satmath#satsubjecttestmath#mathsathome#satmathtutor#mathematiciansatwork#satmathclass#satmathprep#satmath2#satmathlevel2#satmaths#satmath1#satmath800#mathsatyourfingertips#satmathclub#satmathematics#satmathtutord#satsubjecttestmaths#satmathquestions#satmathtutoring#satmathonline#sattestprep#satexamprep#satsprep#satexamsprep#prepsat#satpreparation#satprepclass#satprepcourse#rationalnumbers#simplifyingfractions
0 notes
Video
youtube
Cracking SAT Math: Simplifying Fractions & Rational Numbers - Welcome to your comprehensive SAT math preparation session! In this video, we'll delve into the world of rational numbers, equipping you with essential skills to tackle SAT math questions with confidence. The SAT Math section assesses your mathematical skills, including your ability to work with fractions and rational numbers. These foundational concepts are essential not only for the SAT but also for various aspects of mathematics and real-life situations. In this article, we will explore and solve three SAT Math questions involving simplifying fractions and rational numbers. By the end of this journey, you will have a solid grasp of these concepts and be better prepared for the SAT Math section. 𝐐𝐮𝐞𝐬𝐭𝐢𝐨𝐧 𝟏 : Simplify (-4/5) × (3/7) × (15/16) × (-14/9) to its simplest form. 𝐐𝐮𝐞𝐬𝐭𝐢𝐨𝐧 𝟐: Calculate the sum of the rational numbers -5/16 and 7/12. 𝐐𝐮𝐞𝐬𝐭𝐢𝐨𝐧 𝟑: Determine the number that should be added to 7/12 to obtain 4/15. Mastering fractions and rational numbers is essential for success in the SAT Math section and beyond. These concepts are foundational in various mathematical topics, from algebra to calculus, and have practical applications in everyday life. By understanding how to simplify fractions and work with rational numbers, you not only improve your test-taking skills but also enhance your overall mathematical proficiency. Our experienced instructor will guide you through these problems, providing clear and insightful solutions. Understanding rational numbers is fundamental for success in the SAT math section, and we're here to ensure you not only find the right answers but also grasp the underlying concepts. By the end of this video, you'll feel more confident and prepared to conquer SAT math challenges. Don't forget to hit the like button, subscribe to our channel, and ring the notification bell for more SAT math practice, tips, and strategies. Let's embark on this math journey together, gearing up for SAT success! 🚀📚
0 notes
Video
youtube
SAT Math: Mastering Algebraic Identities - (11x + 3y)² - (11x - 3y)² Hello, SAT math explorers! 📐 Join me in unraveling the enigmatic world of algebraic expressions as we tackle an intriguing SAT question together. In this video, we'll delve into the realm of expression simplification and embark on a journey of logical deduction to identify the expression that is NOT equivalent to the given expression. Get ready to enhance your algebraic reasoning and elevate your problem-solving prowess! ✨ In this SAT question, we'll demystify the intricacies of algebraic expressions and put our expression simplification skills to the test. Armed with algebraic techniques and analytical precision, we'll navigate through each option and discern the expression that diverges from the given expression's equivalency. Through meticulous reasoning and systematic analysis, we'll uncover the answer that sets itself apart from the rest. The path to expression mastery awaits! ⚔️🔍 Join me on this quest for algebraic clarity. As we delve into the options A) through D), we'll unveil the step-by-step simplification of the given expression and compare it to each choice. By the end of this video, you'll have gained valuable insights into dissecting algebraic equivalencies, empowering you to confidently approach similar challenges on your SAT journey. Don't forget to like, subscribe, and hit the notification bell for more exhilarating SAT math insights. Let's decode the secrets of algebraic expressions and conquer the world of math! 🔔📚
0 notes
Video
youtube
Mastering SAT Math: Algebraic Expressions - Solving Equations with Expon... Greetings, SAT math enthusiasts! 📚✏️ Are you ready to tackle a challenging algebraic expression problem that tests your skills in working with exponents? In today's video, we're diving deep into the world of algebraic equations. Here's the problem we'll be solving together: "If x² - y² = 12xy, find the value of x²/y² + y²/x²." This question requires a strong understanding of algebraic expressions, exponents, and the ability to simplify equations effectively. We'll guide you step by step through the solution process, ensuring that you grasp the concept and technique needed to excel in similar SAT math questions. By the end of this tutorial, you'll feel confident in your ability to handle algebraic expressions involving exponents and equations. Whether you're preparing for the SAT or simply aiming to enhance your math skills, this video is a valuable resource. Join us on this mathematical journey as we unravel the solution to this SAT-style algebraic expression problem. If you found this video helpful and want to excel in your SAT math section, don't forget to hit the like button and subscribe for more enriching math tutorials, problem-solving strategies, and SAT tips. Let's master algebraic expressions and conquer the SAT together! 🚀✏️
0 notes
Video
youtube
Cracking SAT Math: Algebraic Expression Simplification #satmath #satprep...
#youtube#sat#satmath#satmathprep#satmathtest#satmathpreparation#sat preparation#satpreparation#satmathtutor
1 note
·
View note
Video
youtube
Mastering Algebraic Expression Multiplication: Exploring (5x - 3x - 4x²)...
#youtube#sat#satmath#sat maths#sat tutor#sattutor#sat test#sat prep#satprep#satpreparation#sat preparation#sattest#satmathtest#satmathprep
0 notes
Video
youtube
Cracking Algebraic Expression Subtraction: Solving a Multi-Term Challeng...
0 notes
Video
youtube
Mastering Algebraic Expression Addition: Solving 3 Equations in 1! #satm...
0 notes
Video
youtube
Mastering Algebraic Equations: Solving for x² + 1/x² with x + 1/x = 3 #s...
#youtube#satmath#satmaths#sat math#sat test#sattest#sat prep#satprep#satmathtest#satmathprep#sat preparation#satpreparation
0 notes