#SATMathTips
Explore tagged Tumblr posts
Text

📚 Master SAT Math with Y2 Academy! Our expert tips will help you conquer the math section and boost your scores. Don't miss out!
Contact us today!!
☎ (856) 888 2123
🌎 https://www.y2academy.com/sat-math-tips/
#SATMathTips #Y2Academy #SATPrep #sattestprep #satmath #satmathtutor
0 notes
Text

The SAT Math section assesses your mathematical skills, including your ability to work with numbers and expressions. Understanding how to analyze and calculate properties of two-digit numbers is essential for solving math problems on the SAT and in real-life scenarios. In this video, we will explore a SAT Math question that involves finding the sum of the digits in a two-digit number: "In a two-digit number, the units digit is x, and the tens digit is (x + 3). What is the sum of the digits in the number?" The correct answer is Option D) 11x + 30. By the end of this exploration, you will have a clear understanding of how to find the sum of digits in such numbers, improving your performance on the SAT Math section.
Question: Finding the Sum of Digits in a Two-Digit Number
Question: In a two-digit number, the units digit is x, and the tens digit is (x + 3). What is the sum of the digits in the number?
Options:
A) 11x + 3
B) 2x + 3
C) 3 + x
D) 11x + 30
Explanation and Key Concepts: When dealing with two-digit numbers, you can represent them as 10 times the tens digit plus the units digit. In this problem, the tens digit is (x + 3), and the units digit is 'x.' The sum of the digits is found by adding the tens and units digits, which leads to the expression 11x + 30.
Analyzing and calculating properties of two-digit numbers is an essential skill for the SAT Math section and beyond. This skill allows you to manipulate numbers and solve various mathematical problems efficiently. By mastering this skill, you'll not only excel on the SAT but also enhance your overall mathematical proficiency, which can be applied to various real-life scenarios.
#SATMathTips#AlgebraSimplification#MathExpression#SATMathPrep#MathematicsTutorial#SATMathProblems#TestPreparation#SATExamTips#MathSimplification#SATMathematics#SATTest#MathHelp#ProblemSolving#SATMathSkills#AlgebraicExpression#MathematicalEquivalence#SATStudy#MathExplained#SATPreparation#MathConcepts
0 notes
Text

The SAT Math section assesses your mathematical skills, including your ability to perform operations with algebraic expressions and identify their differences. Understanding how to find the difference between two expressions is essential not only for the SAT but also for various mathematical and real-life scenarios. In this video, we will explore a SAT Math question that involves finding the difference between two algebraic expressions: "What is the difference between (3a + 2b) and (-2a - 5b)?" The correct answer is Option A) 5a + 7b. By the end of this exploration, you will have a clear understanding of how to find the difference of algebraic expressions, enhancing your performance on the SAT Math section.
Question: Finding the Difference of Algebraic Expressions
Question: What is the difference between (3a + 2b) and (-2a - 5b)?
Options:
A) 5a + 7b
B) -5a - 7b
C) 5a - 7b
D) a - 3b
Correct Answer: Option A) 5a + 7b
Explanation and Key Concepts: Finding the difference between two algebraic expressions involves subtracting one expression from the other and then combining like terms. Remember that subtracting a negative expression is equivalent to adding the positive expression.
Understanding how to find the difference between algebraic expressions is a fundamental skill for the SAT Math section and beyond. This skill is applicable in various mathematical and real-world scenarios, allowing you to analyze differences and make informed decisions. By mastering this skill, you'll not only excel on the SAT but also enhance your overall mathematical proficiency.
#SATMathTips#AlgebraSimplification#MathExpression#SATMathPrep#MathematicsTutorial#SATMathProblems#TestPreparation#SATExamTips#MathSimplification#SATMathematics#SATTest#MathHelp#ProblemSolving#SATMathSkills#AlgebraicExpression#MathematicalEquivalence#SATStudy#MathExplained#SATPreparation#MathConcepts
0 notes
Text
SAT Math - How to find the value of x + y + z if x + y = 5, y + z = 7 and z + x = 12.
The SAT Math section assesses your ability to work with various mathematical concepts, including solving systems of linear equations. This skill is not only crucial for the SAT but also for real-world applications in fields like science, engineering, and economics. In this video, https://www.youtube.com/watch?v=34Cdnk9i_uo we will explore a SAT Math question that involves solving a system of three linear equations: "If x + y = 5, y + z = 7, and z + x = 12, what is the value of x + y + z?" The correct answer is Option A) 12. By the end of this exploration, you will have a clear understanding of how to solve systems of linear equations, enhancing your performance on the SAT Math section.
Question: Solving a System of Linear Equations
Question: If x + y = 5, y + z = 7, and z + x = 12, what is the value of x + y + z?
Options: A) 12 B) 2 C) 5 D) 24
Explanation and Key Concepts: Solving a system of linear equations involves finding values for the variables that satisfy all the equations simultaneously. In this case, we used the method of adding the equations together to eliminate one variable and isolate x + y + z. It's essential to perform the same operation (addition in this case) to all equations in the system to maintain equality.
Solving systems of linear equations is a fundamental skill in mathematics and has applications in various fields. Whether you encounter such problems on the SAT Math section or in real-life situations, the ability to find solutions to systems of equations is invaluable. By mastering this skill, you'll not only excel on the SAT but also be well-equipped for mathematical challenges in the future.
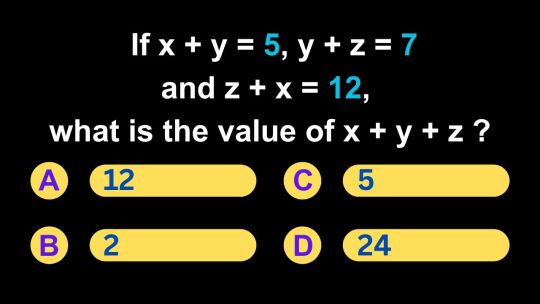
#SATMathTips#AlgebraSimplification#MathExpression#SATMathPrep#MathematicsTutorial#SATMathProblems#TestPreparation#SATExamTips#MathSimplification#SATMathematics#SATTest#MathHelp#ProblemSolving#SATMathSkills#AlgebraicExpression#MathematicalEquivalence#SATStudy#MathExplained#SATPreparation#MathConcepts
0 notes
Text

Welcome to another SAT math session! 📚 Today, we're diving deep into fractions comparison, a crucial skill for acing the SAT math section. We'll compare fractions step by step, and I'll walk you through solving questions like:
Comparing 5/8 and 7/12
Analyzing 5/9 and 11/15
Evaluating 11/12 and 15/16
The SAT Math section assesses your mathematical skills and ability to work with various concepts, including fractions. Comparing fractions is a fundamental skill, both for standardized tests like the SAT and for practical life situations. In this article, we will tackle a series of SAT Math questions that involve comparing fractions and determining their relationships. By the end of this exploration, you will have a firm grasp of comparing fractions and be better prepared to excel in this aspect of the SAT Math section.
Comparing fractions is a fundamental skill in mathematics, and it plays a crucial role in various mathematical concepts and real-life applications. Mastery of this skill is essential not only for the SAT Math section but also for everyday problem-solving. By understanding the techniques for comparing fractions, you can confidently tackle SAT Math questions that involve these concepts and strengthen your overall mathematical proficiency.
Whether you're a seasoned math enthusiast or preparing for the SAT, this video offers valuable insights and practice to boost your confidence.
Don't forget to hit the like button and subscribe for more SAT test prep tips, tricks, and strategies. Let's tackle fractions comparison together! 🚀
#shorts#satmathprep#satmath#satmaths#satmathtestprep#sattestprep#satpreparation#algebraicexpressions#mathproblemsolving#satmathpractice#YouCanLearnAnything#satmathreview#satmathtips#satmathwalkthrough#satmathtricks#satmathquestions#satmathpractice2023#satmathsection#satmathconcepts#satmathtipstricksandstrategies#satmathdigital#satmath2023
0 notes
Text
youtube

Welcome to another SAT math tutorial where we demystify the art of converting improper fractions into mixed fractions! This skill is indispensable for acing SAT math questions involving fractions, and we're here to make it simple.
Fractions are a fundamental concept in mathematics, representing parts of a whole or ratios between quantities. Understanding fractions is essential in various mathematical applications and daily life. One aspect of working with fractions is converting improper fractions to mixed fractions. In this article, we will explore the process of converting improper fractions into mixed fractions through a series of examples. By the end of this journey, you will be proficient in this mathematical transformation.
Now, let's explore the conversion process through examples.
Question 1: Convert 38/7 into a mixed fraction.
Question 2: Convert 47/15 into a mixed fraction.
Question 3: Convert 189/16 into a mixed fraction.
By the end of this video, you'll be well-equipped to convert improper fractions into mixed fractions confidently. Don't forget to like, subscribe, and hit the notification bell for more SAT math practice, tips, and strategies.
Join us in mastering SAT math and boosting your performance on test day! 🚀📚
#satmath#satmathpractice#satmaths#YouCanLearnAnything#satmathreview#satmathtips#satmathprep#satmathwalkthrough#satmathtricks#satmathquestions#satmathpractice2023#satmathsection#satmathconcepts#satmathtipstricksandstrategies#satmathdigital#satmath2023#shorts#satmathtestprep#sattestprep#fractions#mixedfractions#satpreparation#Youtube
0 notes
Text
youtube
Welcome to our SAT math practice session, where we're tackling the art of converting mixed fractions to improper fractions! If you've ever wondered how to master this skill for the SAT math section, you're in the right place.
Fractions are fundamental components of mathematics that represent parts of a whole or ratios between quantities. In many mathematical scenarios, it is necessary to convert mixed fractions (also known as mixed numbers) into improper fractions. This transformation simplifies calculations and facilitates comparisons. In this article, we will delve into the process of converting mixed fractions into improper fractions, using several examples to demonstrate the method. By the end of this journey, you will have a solid understanding of this essential mathematical skill.
Now, let's explore the process of converting mixed fractions to improper fractions through a series of examples.
Question 1: Convert 1³/₄ to an improper fraction.
Question 2: Convert 4⁵/₇ to an improper fraction.
Question 3: Convert 7⁹/₁₃ to an improper fraction.
Question 4: Convert 12⁶/₂₅ to an improper fraction.
By the end of this video, you'll have a solid grasp of this concept, allowing you to tackle similar SAT math questions confidently.
Don't forget to hit the like button, subscribe to our channel, and ring the notification bell for more SAT math practice, tips, and strategies. Join us in mastering SAT math and boosting your confidence on test day! 🚀📚
#shorts#satmathprep#satmath#satmaths#satmathtestprep#sattestprep#sattest#satpreparation#SATMath#AlgebraicExpression#MathProblemSolving#satmathpractice#YouCanLearnAnything#satmathreview#satmathtips#satmathwalkthrough#satmathtricks#satmathquestions#satmathpractice2023#satmathsection#satmathconcepts#satmathtipstricksandstrategies#satmathdigital#satmath2023#Youtube
0 notes
Photo

Join us for SAT prep classes and ace the test with flying colors! Our expert instructors will have you #y2academy and nailing those practice exams in no time. To know more, visit y2academy.com #SATprep #SATmath #SATtutor #SATtestprep #SATstudyguide #SATstudy #SATmathtutor #SATmathprep #SATmathstudy #SATmathtips #SATmathtricks #SATmathstrategies #SATmathskills #SATmathpractice #SATmathproblems #SATmathsuccess #testprep https://www.instagram.com/p/CnqhtffvW0E/?igshid=NGJjMDIxMWI=
#y2academy#satprep#satmath#sattutor#sattestprep#satstudyguide#satstudy#satmathtutor#satmathprep#satmathstudy#satmathtips#satmathtricks#satmathstrategies#satmathskills#satmathpractice#satmathproblems#satmathsuccess#testprep
0 notes