#mathematically impossible to divide anything by 0
Explore tagged Tumblr posts
Text
Okay this is going to be a bit more venty than usual but I've seen a post about complex numbers that's annoyed me.
The only reason you are less willing to accept the existence of imaginary numbers is you aren't taught it in a way that helps build intuition nor from as young an age.
Complex numbers have been around for centuries. They aren't some new fangled thing that are mysterious to mathematicians. Part of the non-mathematician's conception of imaginary numbers certainly isn't helped by their name but I have to say I think the internet and clickbait are a lot to blame for that too.
A lot of mathematics is invented by thinking "what if..." and rolling with it to see if you can draw anything meaningful from it. "What if numbers less than 0 exist?", well then you have given meaning to something like 2-7. "What if we could divide any two integers?", now you can talk about what 3/7 means. Asking "what if square roots of negative numbers did exist?" let's us explore whether √(-1) would give us something with consistent and useful properties and it turns out it does (technically we just declare i²=-1 and i=-√(-1) does everything just as well).
"You can't take the square root of a negative number" is drilled into pupils heads at school when really the message should be a more subtle "there aren't any real numbers that are the square root of a negative number". It's a subtle but important difference. It's exactly like saying "there aren't any natural numbers x such that for naturals numbers y and z with z>y we have x=y-z". You'd be pretty hard pressed to find anyone saying that the latter is impossible.
I don't really know how to end this. I'm just frustrated
212 notes
·
View notes
Text
right where was i? oh right, i was about to talk about the eigendecompositions. lets go!
(fair warning: this part might be a bit more advanced than the previous one. ill try to explain as well as possible though)
maybe youve worked with matrices before, and youve learned that theres some things called the geometric and algebraic multiplicity of matrices. if theyre equal, you can write the matrix in a diagonal form, if not you cant. lets use C-H to formalise that idea!
lets show you what im talking about first. earlier, we had a matrix A with characteristic polynomial x(x - 7). since all the eigenvalues are distinct, you can do a change of basis and write it like this:
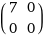
lets ignore the change of basis part (since C-H cant really help with that anyway). basically, this diagonal matrix does the same thing as A if you ignore the rotating and streching of the plane. however, this process would be impossible for this matrix (lets call her B):
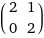
B has characteristic polynomial (x - 2)^2 (check that!). the algebraic multiplicity of the eigenvalue 2 is the exponent belonging to (x - 2), so thats 2. the geometric multiplicity is the dimension of the kernel space {y: (2 - A)y = 0}, which is 1. those arent equal, so we cant make a diagonal form. to check this, you need to do lots of calculations, and i prefer not to. let's use C-H for the same problem somehow.
lets take a look at this matrix, C:
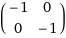
it has characteristic polynomial (x + 1)^2, so (C + 1)^2 = 0. however, notice that C + 1 is also zero! C-H tells us that C filled in in its characteristic polynomial is zero, but it doesnt say anything about its divisors. the smallest degree polynomial that returns zero this way is called the minimal polynomial.
given a characteristic polynomial P of a matrix A, you can find the minimal polynomial M using these rules:
M(A) = 0
M divides P
every factor of P appears in M at least once
M only contains distinct linear factors if and only if A can be put in a diagonal form
lets try this for our matrix A: we had P(x) = x(x - 7). every factor appears only once, so M(x) must also be x(x - 7). the first and second rule are automatically satisfied, and M = P only contains distinct linear factors. indeed, A can be put in a diagonal form, as we saw earlier.
now for B, with P(x) = (x - 2)^2. we have two candidates for M: by rule 2, we either have M(x) = x - 2, or M(x) = (x - 2)^2. but notice that B - 2 is not zero! thus, we must have the second option, M(x) = (x - 2)^2. the factor (x - 2) appears twice, so M does not contain distinct linear factors, and B cannot be put in a diagonal form.
finally, for C we have P(x) = (x - 2)^2 and M(x) = x - 2 (since C - 2 = 0, as we saw earlier). thus, by rule 4, C can be put in a diagonal form (it already is, so thats clear).
so thats it :3 my favourite theorem in mathematics, i hope you enjoyed my infodump lmaoo
One thing about me is I infodump about math subjects on request
238 notes
·
View notes
Text
Benefits of 0 (zero) and ``impossible'' and ``indefinite'': Mathematics Note- 3 (essay)

The number "0: zero" invented by Indians had an impact not only on mathematics until then, but also on society.
The utility of zero is two-fold: 1) the number that bisects the number line between +1 and -1, and 2) the symbol for "empty" in the weighted number system. A number of 1200 indicates that the last two digits are vacant.
Such a numbering system is simple, for example, it is hopelessly difficult to express a large number such as 123456 using Roman numerals. The power of the positional notation is obvious. I think this difference appears especially in the fields of commerce and warfare.
Zero, which indicates vacancy, is thought to reflect the 'emptiness' of Indian philosophy. ... This mysterious number: 0 (zero).
I believe that there were two major trends in mathematics: Greek geometry and Indian arithmetic. The former contributed to the rigor of the proof, and the latter contributed to practical convenience. Modern and contemporary mathematics developed through the combination of these two.
Zero has an interesting property. "If you multiply by zero, it's all zero", then "What happens if you divide by zero?"
There are two types, A/0 and 0/0. (A is a non-zero number)
If you return to the state before the actual act of breaking each,
(Even if you look at the result of dividing by zero, the consideration will be at a dead end, so consider the state before that.)
A/0 ・・・You can find X from 0*X=A in a linear equation, but if you multiply any number by zero, it will be zero, and it will never be a non-zero A, so "this kind of formula doesn't hold" , so such a number X does not exist at all: Impossible.
0/0... In this case, it is also a linear equation, 0*X=0
The answer is "X can be 'anything' because any number multiplied by it will be zero. ” Any number will be the answer. : Indefinite .
The number zero has a very special property, and in mathematics, it has produced various theories, just like ∞ (infinity).
4 notes
·
View notes
Text


nullic/nullian (100% open to name suggestions): orientation version of gendernull. aroace but undefined, like dividing by 0. void, nonexistent, impossible. not meant to be combined with anything else. can also be non-SAM ace/aro
symbol: negative space of ∅ (mathematical null symbol). reminiscent of voidpunk and a black hole like from the singularian flag
colors: red version from gendernull flag, purples dark void colors. not meant to pull from any other flag except for similar weight with gendernull
i made this with one specific character in mind but figured i'd post it
78 notes
·
View notes
Text
Stop Freaking Out About Gödel: How I Learned to Stop Worrying and Love the Incompleteness Theorems
So when I was in college, I noticed something a bit concerning: a rather large portion of people involved in hard sciences were totally unfamiliar with even basic philosophy of science. For example, when I talked to other science majors I discovered that the majority of them seemingly didn’t know the difference between a theory and a law. The most frequent definition I got was that theories are still somewhat uncertain, whereas laws have been proven to be true and are more or less never wrong. This is incorrect – first of all, a scientific law can absolutely be wrong. Throughout history, even well-established scientific laws often end up being modified or thrown out entirely as new evidence comes to light. For instance, it turns out Newton’s Laws of Motion are only accurate for large objects moving slowly; things that are extremely small or moving close to the speed of light behave by entirely different rules. The actual difference between a theory and a law is that a law has to be a concise description of how something in nature behaves that can usually be stated in full in one or two sentences, or more ideally an equation. For example, the Second Law of Thermodynamics states that the entropy of an isolated system never decreases, or simply ∆S≥0. A theory, on the other hand, is an interconnected collection of ideas that attempts to explain a natural phenomenon or range of phenomena, and will make multiple falsifiable predictions. It’s possible for a scientist to devote their entire lives to improving humanity’s understanding of a single scientific theory – biology’s theory of evolution is a good example.
Now at this point you might be saying “So what? You’re just nitpicking at semantics.” I would argue that misunderstanding the theory/law distinction betrays a more fundamental lack of grasp on the scientific method. Once we start conceptualizing certain ideas, even implicitly, as infallible or otherwise not worth questioning anymore, we start veering away from the realm of science and into the realm of dogma. I have a strong suspicion that a lot of the weird STEM elitism that’s so prevalent these days is a result of widespread illiteracy as to what science itself is at a basic level – otherwise it would become obvious how ultimately inseparable hard science is from soft science, from philosophy, from art. I could go on about this for ten more pages but this isn’t really the topic I want to talk about right now. My essential point is that it’s very easy for people who are otherwise highly intelligent and highly competent in their field to lack proper understanding of its underlying philosophy.
The reason I bring this up is because I am about to argue that almost everyone is interpreting Gödel’s Incompleteness Theorems wildly inaccurately. More specifically, I’m aiming to demonstrate that the idea that a mathematical conjecture can be “true but unprovable” is tautologically false. This is a misconception that stems from confusion over what constitutes mathematical truth – which is actually a philosophy problem, not a math problem. If you want to be able to say anything at all about truth or falsehood in this context, first you’re going to need a coherent and precise definition for mathematics itself.
Let’s start by trying to answer a narrower question: what are numbers? In what manner can numbers be said to exist? Can you look at a number? Can you touch a number? I can draw the numeral “4” on a sheet of paper, but that’s not really the number four, it’s just an arbitrary symbol we chose to represent it. If tomorrow everyone decided that we were going to switch the numerals for four and five (such that “5” now means four and vice versa), nothing about how math works would change, it would just look slightly different on paper. So then a number definitely isn’t a physical object like a proton or a chair or a planet. Now at this point you could argue that perhaps numbers are a property that things in the real world can have – for example, if an H+ ion has a positive electric charge, most people would agree that its charge is something that that exists in the physical world despite the fact that it can’t exist independently from the ion. Analogously, you can count a group of apples and always get the same results; if there are four apples then there are four apples. You can even use arithmetic to make accurate predictions about how many apples there will be if you add more, remove some, or divide them into groups. So you could claim: therefore, numbers must be real i.e. they must somehow exist in the universe independent of human thought.
However, this line of argument fails pretty quickly once you consider the fact that the all the rules of arithmetic change relative to how you happen to be looking at the problem. For instance, suppose you’re trying to figure out how many people you can fit in an elevator. You’re inevitably going to end up using the natural numbers – we can all reasonably agree you can’t have a fraction of a person (you could cut a human being in half, but they would cease to meaningfully be a person at this point). You decide you can cram about eight people in before running out of room, but then realize you forgot to consider the elevator’s weight capacity. If it can safely lift about two tons, then you’re also going to have to measure the combined weight of everything it’s carrying in terms of fractions of tons. Suddenly the math you have to use changes from discrete to continuous, which is a really important difference; there’s no way to have between one and two people, but you can easily measure a weight between one and two tons (say 1.5 tons), and then if you want you theorize a possible weight that’s between one and the weight you just measured (say 1.25 tons), and so on and so on indefinitely. This is all fairly straightforward, but it presents a significant problem if you want to contend that these numbers exist independently of human cognition. Which set of rules is correct? If numbers objectively exist then it logically must follow that any given number either can be divided into arbitrarily smaller parts, or cannot be. Do negative numbers really exist? As far as we’re aware it’s impossible for an object to have negative mass, and you certainly can’t have a negative number of people. Do complex numbers exist?
Another problem: the number we get when we determine the mass of a given object will be different depending on what units of measure we’re using. If we switch from using kilograms to pound-masses, none of the physical properties of the object have changed, but we’re now measuring completely different numbers. This is because mass is an objective physical property, but numbers are simply a system we’ve come up with to help us describe this. An object inherently has mass, but does not inherently have two-ness or four-ness or the like. Mathematics, then, is not an objective reality but merely a human invention we sometimes use to describe objective reality, somewhat conceptually akin to a natural language like English or Mandarin. Once we grasp this, it becomes possible to define math in a precise and consistent matter (and hence mathematical truth). All mathematical systems can be ultimately be characterized in terms of sets of symbols, axioms, and rules of inference. Mathematics, therefore, is simply the study of axiomatic systems.
In this context, Gödel’s Incompleteness Theorems are less “existential crisis inducing mind-screw” and more “fairly intuitive idea that perhaps should have been obvious in retrospect.” The second incompleteness theorem can be approximately stated as: “for any consistent system F within which a certain amount of elementary arithmetic can be carried out, the consistency of F cannot be proved in F itself.” How could any system of axioms conceivably prove itself consistent? By the logical principle of explosion, we know that in any inconsistent system we can prove literally any proposition that the system can express, meaning an inconsistent system would necessarily be able to prove itself consistent according to its own rules. Therefore, it would be impossible for us to distinguish a hypothetical consistent math system that could somehow prove its own consistency versus an inconsistent system that could prove its own consistency due to some internal contradiction we haven’t yet discovered.
The first theorem states, roughly: “Any consistent formal system F within which a certain amount of elementary arithmetic can be carried out is incomplete; i.e., there are statements of the language of F which can neither be proved nor disproved in F.” Remember, math isn’t “about” anything, it’s a series of games in which you manipulate strings of symbols according to a set of made up rules. No axiomatic system is fundamentally any more real than any other; some of these systems we study because they help us describe things in the real world, some of these systems we study because they have interesting properties, and some of them we don’t study because they’re neither useful nor interesting (such as systems that have been proven to be inconsistent), but ultimately what determines what kind of math is used or not is simple pragmatism. Thus, the only meaningful way to define mathematical truth is such that a statement is true within the context of a given math system if and only if it can be proven with the axioms provided by said system. The idea that a proposition could be “true but unprovable” is equivalent to saying that a statement simultaneously both can be proven and cannot be proven. A mathematical theorem is just a string of symbols; if you can produce this string within a given formal system then it is true, if you can produce its negation then it is false, and if you can neither produce the string nor its negation then it is undecidable i.e. independent of the axiomatic system you’re currently using. The first incompleteness theorem demonstrates that all relevant formal mathematical systems will necessarily contain such undecidable statements, but we should no more be upset about this than we should be upset about the fact that there are possible positions on a chess board that can’t be arrived at through normal play. If the math system you’re using doesn’t end up having the properties you want it to have, then the solution is to make up a system that does have those properties (side note: this is why everyone should just accept the Generalized Continuum Hypothesis as an axiom and get on with our lives instead of being obnoxious about it). The idea of “completeness” was always impossible and never really meant anything – it’s time to stop mourning Gödel and embrace mathematics for what it really is.
82 notes
·
View notes
Text
Something awesome - cryptography chapter
Below is what I’ve completed for the cryptography chapter which includes the research and write-ups which I blogged about earlier. Altogether this chapter was about 2.7k words (yikes)
What is cryptography?
Cryptography is the art of encrypting data. If you ever developed a secret code as a kid, so you and your friend could communicate without anyone else knowing what you’re saying, then you’ve already had experience with writing your own secret code!
Cryptography is done in many ways, with some of the most common being through the use of codes and ciphers. This guide will cover a few of the more basic ones, and provide pointers to more complex ciphers for those who are interested.
Why do we need cryptography?
If we didn’t encrypt any of our sensitive information or messages over the internet, then potential attackers could easily steal your private data or read confidential messages. This is why cryptography is so important - because it provides us with confidentiality.
Cryptography is already being used in many ways in your daily life - you just don’t see it happening. For example, one of the key aspects of cryptography is what is called a hash. These are used to authenticate log-ins like your passwords whenever you log in to an account.
Below are some of the main examples of how you can encrypt your data:
Ciphers
The basic concept of a cipher is you have a message, usually in plain english, that you want to make secret (called encrypting your message). This is called your ‘plaintext’. You then apply the rules of your chosen cipher to a plaintext, to get a secret message which is called your ‘ciphertext’.
Then, you send your secret message to your friend who also knows the rules of the cipher you chose to use. Using that knowledge, they then decrypt the ciphertext you gave them, to reveal the original message in plain english.
You can think about this like something that you might be more familiar with. If you know what pig latin is, for every word that you say take the first letter of the word and move it to the end of the word and add the sound “ay”.
So if I wanted to say “pig latin”, which is my plaintext, in pig latin I would use the above rule to transform “pig latin” into “igpay atinlay”, which is my ciphertext. For someone to understand my ciphertext, they would have to know the rules of pig latin in order to decrypt and find my original message.
In this section we’ll be covering some of the most common ciphers:
Caesar Cipher
A secret ‘key’ is chosen between the people who want to communicate secretly, which will be a number between 0 and 25. Then, each letter in the message is shifted forward or backward by that key to receive the encrypted message.
For example, “This is an example” with a forward shift key of 1 gives the encrypted message: “Uijt jt bo fybnqmf”
Although the message may seem very secret, in reality it’s actually very easy to break! All you have to do is just apply all possible 26 forward and backward shifts and only one key will likely give an answer which looks like plain english.
While this may take a lot of time for someone to do by hand, because of computers, this process can be done a lot faster.
You can find a tool to encrypt and decrypt your own messages using the Caesar cipher here. Simply change the message in the left box to what you want to make secret, and then use the + or - buttons to choose the ‘key’ for which to shift your message. You should find your secret encrypted message in the right box!
Substitution Cipher
Unlike a Caesar cipher, where you are shifting the whole message by a certain amount, in a Substitution Cipher you choose each different letter in your message, and shift that by a different amount.
Basically what this means is for each letter in the alphabet, you choose a different letter that you will replace it with when you encrypt your message. For example, you could choose to substitute the letter ‘a’ with the letter ‘p’ when performing your substitution cipher. You would then do this process for every letter in the alphabet until you get something like:
plain alphabet : abcdefghijklmnopqrstuvwxyz
cipher alphabet: phqgiumeaylnofdxjkrcvstzwb
An example encryption using the above key:
plaintext : defend the east wall of the castle
ciphertext: giuifg cei iprc tpnn du cei qprcni
You might think that this way of encrypting your messages is way better than the Caesar Cipher, because it would be much harder to figure out. After all, if an outside person was trying to decrypt your message, the would have to go through every possible substitution.
However, something that we don’t consider is that this cipher actually preserves letter frequency. In the english language, some letters appear in words more than others. However, when it comes to cracking substitution ciphers, what we can do is count through all the times we see a certain letter, and try and compare that to what we see in normal english.
Remember this little name: “etaoin shrdlu”. This tells you the most frequently occurring letters in the english language in descending order. So if you see a certain letter like ‘z’ appearing a lot more frequently than others, chances are it could be either an ‘e’ or a ‘t’.
Substitution ciphers also don’t do anything to hide the length of words in your message. So if you have a three-letter word like ‘zcy’ in your message, chances are it would be a word like ‘the’.
Using all the above, it actually becomes a lot easier than you think to decrypt a substitution cipher. You can have a try for yourself using this link.
Vignere Cipher
The Vignere cipher uses a special table and a key to generate the ciphertext.

In addition to the plaintext, the Vigenere cipher also requires a keyword, which is repeated so that the total length is equal to that of the plaintext. For example, suppose the plaintext is MICHIGAN TECHNOLOGICAL UNIVERSITY and the keyword is HOUGHTON. Then, the keyword must be repeated as follows:
MICHIGAN TECHNOLOGICAL UNIVERSITY
HOUGHTON HOUGHTONHOUGH TONHOUGNTO
We then remove all spaces and punctuation, and convert all letters to upper case, finally dividing the result into 5-letter blocks. As a result, the above plaintext and keyword become the following:
MICHI GANTE CHNOL OGICA LUNIV ERSIT Y
HOUGH TONHO UGHTO NHOUG HTONH OUGHT O
To encrypt, pick a letter in the plaintext and its corresponding letter in the keyword, use the keyword letter and the plaintext letter as the row index and column index, respectively, and the entry at the row-column intersection is the letter in the ciphertext. For example, the first letter in the plaintext is M and its corresponding keyword letter is H. This means that the row of H and the column of M are used, and the entry T at the intersection is the encrypted result.

Repeat this process to generate your ciphertext!
Caesar Cipher
If you want to have a further look into different ciphers, try these resources:
Affine Cipher
Wheel Cipher
Playfair Cipher
Hashing
To summarise what a hash is, it requires two things:
A hash function, which is any kind of mathematical function that takes input and produces some output
A message that is given as input to the hash function.
There are three main requirements of a good hash function:
It should be easy to calculate the hash value (output of hash function) given a message.
It should be very hard (ideally impossible) to calculate the original message given a hash value.
No two messages should have the same hash value.
Example of the hashing process:

In the above image, the ‘input’ is the message and ‘Digest’ is our hash.
Our ‘cryptographic hash function’ above could have been something as simple as f(x) = 10, where x is the message. It’s easy to calculate the hash value, which fits the first criteria, but it breaks the third criteria. This is because no matter what our message is, the hash will always be the same!
Also, something like f(x) = x, would not be a good cryptographic hash function. With this function It is easy to calculate the hash, and we also avoid collisions, meeting the first and third criteria. However using this function, our message is the exact same thing as our hash, which kind of defeats the purpose of using a hash in the first place!
What do we use hashes in?
As you will see below, hashes are used to store passwords. If we just stored the actual password itself in something like a database, if a hacker or an outside person were to gain access, the would be able to easily gain access to everyone’s accounts. We uses hashes as an extra layer of security.
Even if people see the hashes, the point is that it is a super long and tedious process to try and figure out a password from a hash. You need to know the hash used, and then match every single different input to your unique hash which would take an extremely long time - so much that even trying to get your password wouldn’t be worth the time.
Passwords
Have you ever thought about how the password you use to log in to your computer is stored? etc/passwd is a text file, which contains a list of the system’s accounts, giving for each account some useful information.
What is in a etc/passwd file?
Typical output would include a line like: root:x:0:0:root:/root:/bin/bash
Fields separated by columns in order are:
Username: root
Encrypted password: x
UID: 0
GID: 0
Comment: root
Home directory: /root
Shell: bin/bash
Encrypted password found in etc/shadow file
What is in a etc/shadow file?
Example output of shadow file: root:$6$IGI9prWh$ZHToiAnzeD1Swp.zQzJ/Gv.iViy39EmjVsg3nsZlfejvrAjhmp5jY.1N6aRbjFJVQX8hHmTh7Oly3NzogaH8c1:17770:0:99999:7:::
Fields separated by columns in order are:
Username: root
Encrypted password - Usually password format is set to $id$salt$hashed, The $id is the algorithm used On GNU/Linux as follows:
$1$ is MD5
$2a$ is Blowfish
$2y$ is Blowfish
$5$ is SHA-256
$6$ is SHA-512
So for the example above, we can see that the password is hashed using the SHA-512 algorithm.
You can have a further look into how passwords are stored here
picoCTF writeups - Cryptography:
See my previous blog post here
1 note
·
View note
Text
Can You Smell Infinity?
Astrophysicists have been trying to find out how big the universe is and their inconclusive measurements suggest it could even be infinite. What does philosophy make of that? In order to do certain mathematics, like Sir Isaac Newton's calculus, you can use certain concepts like infinity (the amount without limit) and the infinitesimal which is what you get when you divide something down infinitely. These concepts, or I shall call it a 'conception' (as a technical term) of infinite, has not been mainstream for that long, only really from Newton onwards. Aristotle said whatever could be described using non-finite concepts could also be described using finite concepts; so Aristotle was what is called a 'finitist', and a very influential one until Newton. In blog 11, "What Makes Us for Real?", we discussed whether certain things exist, and we decided that mathematics was a part of the hyper real: What then of the infinite?
The infinite cannot literally exist in the hyper real as you would need infinite storage to store the items, and we live in a finite and digital mind space here on earth. So there must be a massive sphere confusion (see blog 1) somewhere in mathematics as many mathematicians believe in the everyday infinite. We shall discuss why non-finitists believe in the absoluteness of the infinite, and then we will discuss what the infinite is as a conception of the number line and follow on to a more sensible conclusion compatible with the hyper real experience.
It is true that the infinite conception works in mathematics to solve equations. The simplest form of this I can think of is the sum of a geometric progression. This takes a series, and if the series is declining geometrically, will come to a finite value after infinite terms; for example:
1/1 + 1/2 + 1/4 +1/8 + 1/16 ... 1/∞ = 2
Here the first term is the coefficient a=1, and progression is multiplied by the common ratio r=1/2, and the series is summed to infinite terms. Where r<1, this can be proved using algebra to give the formula:
a/(1 - r)
or 1/(1/2) = 2 in our case.
So to conclude this paragraph, there is something that works about infinity that needs to be explained; perhaps how does it work finitely?
In previous blogs (particularly blog 8 on reductionist science), I have mentioned that even in STEM subjects there can be heavy sphere confusion. Here the idea of infinite, like eternal, or all powerful has been absorbed into and from monotheism, and it is probably a nonsense. Even medieval Christian philosophers had a conception of god's eternal property to be outside of time entirely and not infinite. So the familiarity of infinite or eternal cannot hide the possibility that it is an example of a religious theoretical entity, like those in the last blog 18. This infinite likely cannot exist, so not only is it superfluous, but it contradicts the way we can count space & time so can be rejected.
This notion of eternal outside of time is also probably nonsense, but does make two suggestions: The first trivial one is to reject eternal as everything happens in finite time, for time is just a function of change. The second more important one for us is that 'infinite' the conception is not infinite, being a conception. So the infinite is not infinite as many had confused religion with metaphysics, metaphysics with a mental conception, and a conception with a placeholder in an equation. So what then is a hyper real conception that acts as both a placeholder and a concept?
Before we begin on conceptions, we should look a little more broadly at the issues conceptions need to cover. Can impossible things work in mathematics? Yes they do seem to be able to. We have the infinite series, the infinitesimal calculus, and there are others. A simple example of something impossible is the imaginary number i, which is defined as the square root of minus 1, or (√-1). No number multiplied by itself equals -1; yet using i you can solve real world problems of engineering and even some simple algebra:
Suppose you have two lots of partition walls for two square boxes that will reduce the clutter in your bedroom, one by -4m2 of clutter and the other by -9m2 of clutter; and you wanted to make the boxes equal sized rectangles using the existing pieces; how much clutter would they store?
√(-4m2) x √(-9m2) = 2im x 3im = 6i2m2 = -6m2 as i2 = -1
so 2 boxes x -6m2 = -12m2 of clutter. This is not better than -4m2 -9m2 = -13m2 of clutter before, but at least you know that the cost of making them equal and rectangular is +1m2 of extra clutter in your bedroom.
So conceptions such as i, need not be infinite, and can sometimes be used in mathematics, also they are not really existing.
If a conception is not the real thing, then we can treat it as a name for a thing; so implicitly a name is a new type of set as first described in blog 6 on causation. This conception though is more than a normal name; by normal I mean a key for filtering and grouping objects so we can categorise and understand them. A conception is more like a meta name, a description of multiple circumstances or sets: In the case of natural numbers, the name's schema describes increasing +1 from 0 repeatedly without a limit. In the case of i, as a replacement for (√-1), and reversibly as replacing i2 with -1. In the case of a number line, it is the natural numbers increasing and subtracting from zero, each number of which can be divided by any other number to a point on the line. Finally, we can conceptually add an infinite term, and divide by it to create an infinitesimal and so create some place holding names for something that doesn't exist, but can be used to cancel out other series. So what else can be a conception?
I suggest anything that automatically creates a system of names - by which I mean the new sets - is a conception. So you could invent a conception to name every brick in your house by an index linked to a database of baby names; a fairly useless conception, but one you could spontaneously create for Bob, Billie, & Barbara Brick. So conceptions are clearly arbitrary. Conceptions have no ultimate or transcendent existence. We have created them as hyper real artifacts by abstraction from our language.
So conceptions are names attached to more complex descriptions, usually of name schemes, that help us manipulate schematic concepts. I disagree that the manipulations of conceptions are obvious as Wittgenstein says in 'Tractatus Logico-Philosophicus', but I do agree that they have implicit or explicit rules. These rules create a model, and flexing the model within the hyper real can tell you new things about the real and your concepts. For me here it is less interesting whether Wittgenstein was a finitist, but more of more interest in whether he, and therefore we, should be sceptical of the infinite, as I think we should. Having come to this conclusion, what can philosophy say to mathematicians about their working with infinity and some mathematicians' odd views that mathematical objects have transcendent existence?
I don't think philosophers have a lot to say to mathematicians on this topic because mathematicians, like Hilbert with his paradox of the Grand Hotel and the finitists, have already done extensive work themselves. So philosophers can only point out that some mathematicians are taking religious prejudices to work and should rethink their metaphysical assumptions and listen to the finitists. However the use of a finite model called infinity instead of an actual infinity may not always be that important if the placeholder allows the proof to be shown and an answer to be given. The conception of infinity has as much to say about metaphysics and language analysis as maths; so these I will discuss next.
In metaphysics there are two sides to the same argument, the first is the necessary non-existence of infinite properties as I mentioned previously. The other is that if we consider oneness, an axiom I used in blog 12 on axioms, we can suggest that there could be no unity to something if it was infinitely diffuse. There wouldn't be a facility to see the universe as a multidimensional monad, or pulsing with cause and effect as mentioned in blog 6 on causation. As Hilbert pointed out, there would be potentially infinite distances between points on an infinite line. This conclusion suggests distance would stop everything from interacting absolutely. So you couldn't smell infinity because it would be too far away.
In terms of language analysis, a conception is a function of the hyper real (as described in blog 11). We can see that there is more than simple names and propositions (as Wittgenstein described), for a conception is:
1) Named and referenced,
2) Has a schematic,
3) The schematic creates other names or allows substitution with other names,
4) Does not exist as an object (so may be impossible),
5) Is expressed in the hyper real,
6) Is an extension of language,
7) Can be compatible with an implicit logic or model.
Given the language and metaphysical analysis of infinity, we can see some parallels with our finding in the last blog, blog 18. Something has been theorised to exist which probably doesn't, and it became part of our grand theory or religious views. But, how excitingly, we can see that the normal expression of a grand theory is through a conception. So now we have a micro mechanism in language to anchor what we analysed was happening at a macro level in our theorising. We previously talked of making generalisations, now we can see that the language for generalisations are conceptions. From the last blog we know that generalisations/conceptions don't exist as objects, but are just patterns in the hyper real language, moving beyond a sign about signs, or language about names. So a generalisation is just one form of a conception. Specifically, a generalisation allows the substitution of a value loaded general term to take the place of multiple names.
How do we ground conceptions further? We can go further and say that the 'conception' is a conception itself. It is (1) named; (2) it has a schematic; (3) it is substitutable to its subsets including generalisations; (4) it is not an object but exists in language; (5) it is hyper real as we are thinking and writing about it; (6) it does extend language to a new area from Wittgenstein's 'Tractatus...'; and finally (7) it is compatible with the epistemological model of generalisation, induction, and identity mentioned in blog 5 on making generalisations as well as the last blog 18.
This is all very exciting philosophy tying together loose ends, but we can also comment a little more explicitly on rationalism, the belief you can learn new things by reasoning. Flexing a conception, a hyper real model, based on the rules of the schematic, will give logical and mathematical answers to hypotheses. This does not give a clear answer as to why rationalism works or when it will work, but it does explain why we get an answer. If we add in the principle of non-contradiction (see blog 6) and apply the schematic only to applicable real world objects, we can model those objects and learn new things about them rationally. I wouldn't (unlike Wittgenstein) call this information obvious or implicit as it might be complex, emergent, or even chaotic, and certainly not always an obvious tautology.
In the final conclusion, the smell of infinity opens up a lot of further analysis on knowledge, language, and the hyper real. So it is very useful even though we can show infinity doesn't exist in any objective terms. We can also account for infinity without relying on any dodgy metaphysics (like the flawed circularity of Plato's eternal forms), even if infinity has applications that are still partly mysterious within mathematics. I would encourage STEM students amongst others to focus more on the schematic descriptions used in their conceptions as experimenting might yield new mathematical or theoretical architecture, both through substitution and the conscious creating of schematics for new groups of names. As I will discuss in my next blog, this is not really the job of professional philosophers any longer.
#philosophy#metaphysics#mathematics#infinite#infinity#concept#conception#analysis#philosophical#logic#hyper#real#finitist#generalisations#Wittgenstein#theory#analytical
1 note
·
View note
Text
Computing With Random Pulses Promises to Simplify Circuitry and Save Power
Stochastic computing may improve retinal implants, neural networks, and more
Illustration: Mark Montgomery
a.zoom .magnifier { margin: -16px 6px 0 0 !important;
Illustration: Mark Montgomery
In electronics, the past half century has been a steady march away from analog and toward digital. Telephony, music recording and playback, cameras, and radio and television broadcasting have all followed the lead of computing, which had largely gone digital by the middle of the 20th century. Yet many of the signals that computers—and our brains—process are analog. And analog has some inherent advantages: If an analog signal contains small errors, it typically won’t really matter. Nobody cares, for example, if a musical note in a recorded symphony is a smidgen louder or softer than it should actually be. Nor is anyone bothered if a bright area in an image is ever so slightly lighter than reality. Human hearing and vision aren’t sensitive enough to register those subtle differences anyway.
In many instances, there’s no fundamental need for electronic circuitry to first convert such analog quantities into binary numbers for processing in precise and perfectly repeatable ways. And if you could minimize those analog-to-digital conversions, you’d save a considerable amount of energy right there. If you could figure out how to process the analog signals in an energy-conserving fashion, you’ll be even further ahead. This feature would be especially important for situations in which power is very scarce, such as for biomedical implants intended to restore hearing or eyesight.
Yet the benefits of digital over analog are undeniable, which is why you see digital computers so often used to process signals with much more exactitude—and using much more energy—than is really required. An interesting and unconventional compromise is a method called stochastic computing, which processes analog probabilities by means of digital circuits. This largely forgotten technique could significantly improve future retinal implants and machine-learning circuits—to give a couple of applications we’ve investigated—which is why we believe stochastic computing is set for a renaissance.
Stochastic computing begins with a counterintuitive premise—that you should first convert the numbers you need to process into long streams of random binary digits where the probability of finding a 1 in any given position equals the value you’re encoding. Although these long streams are clearly digital, they mimic a key aspect of analog numbers: A minor error somewhere in the bitstream does not significantly affect the outcome. And, best of all, performing basic arithmetic operations on these bitstreams, long though they may be, is simple and highly energy efficient. It’s also worth noting that the human nervous system transfers information by means of sequences of neural impulses that strongly resemble these stochastic bitstreams.
Consider a basic problem: Suppose you’re designing a light dimmer with two separate controls, each of which outputs a digital value representing a fraction between 0 and 1. If one control is fully turned on but the other is at, say, 0.5, you want the light to be at 50 percent brightness. But if both controls are set to 0.5, you want the light to run at 25 percent brightness, and so forth. That is, you want the output to reflect the value of the two control settings multiplied together.
Illustration: David Schneider and Mark Montgomery
By the Numbers: Conventional binary numbers, just like the decimal numbers in everyday use, rely on the concept of place value [left]. Stochastic bitstreams don’t use place value; the value they represent is determined by how often 1s appear [right].
You could, of course, achieve this using a microprocessor to carry out the multiplication. What if, instead, the output of your two controllers was transformed electronically into a random series of 0 or 1 values, where the probability of a 1 appearing at any given position in this stream of bits encodes the value at hand? For example, the number 0.5 can be represented by a bitstream in which a 1 appears 50 percent of the time, but at random points. Elsewhere in the stream, the bits have a value of 0.
Why go through the trouble of converting the number like this? Because basic arithmetic operations on such bitstreams are remarkably easy to accomplish.
Consider the multiplication you need to set the brightness of the light. One of the rules of probability theory states that the probability of two independent events occurring simultaneously is the product of the probabilities of the individual events. That just makes sense. If you flip a penny, the probability that it will land on heads is 50 percent (0.5). It’s the same if you flip a dime. And if you flip both a penny and a dime at the same time, the probability that both will land on heads is the product of the individual probabilities, 0.5 x 0.5 or 0.25, which is to say 25 percent. Because of this property, you can multiply two numbers encoded into bitstreams as probabilities remarkably easily, using just an AND gate.
An AND gate is a digital circuit with two inputs and one output that gives a 1 only if both inputs are 1. It consists of just a few transistors and requires very little energy to operate. Being able to do multiplications with it—rather than, say, programming a microprocessor that contains thousands if not millions of transistors—results in enormous energy savings.
How about addition? Again, suppose we have two bitstreams representing two numbers. Let’s call the probabilities of finding a 1 at any given point in those two bitstreams, respectively, p1 and p 2. If one of these bitstreams has a value of 1 in 60 percent of the bit positions, for example, then the value it represents is 0.6. If the other has a value of 1 in 90 percent of the positions, the value it represents is 0.9. We want to generate a bitstream denoting the sum of those two values, p1 + p2 . Remember that p1 and p2 , like all probabilities, must always lie between 0 (something is impossible) and 1 (something is certain). But p1 + p2 could lie anywhere between 0 and 2, and anything greater than 1 can’t be represented as a probability and thus can’t be encoded as a bitstream.
To sidestep this obstacle, simply divide the quantity of interest (p1 + p2 ) by 2. That value can then be represented by a bitstream, one that is easy to compute: Each bit in it is just a random sample from the two input bitstreams. Half the time, a bit sampled from the first input is transferred to the output; otherwise a bit from the second input is used, effectively averaging the two inputs. The circuit that accomplishes this sampling is again a very rudimentary one, called a multiplexer. With it, addition becomes very easy.
Similarly simple circuits can carry out other arithmetic operations on these bitstreams. In contrast, conventional digital circuits require hundreds if not thousands of transistors to perform arithmetic, depending on the precision required of the results. So stochastic computing offers a way to do some quite involved mathematical manipulations using surprisingly little power.
Illustration: David Schneider and Mark Montgomery
Many Times Better: Using stochastic bitstreams, multiplication can be carried out with a single AND gate. Here two bitstreams, representing 1/2 and 3/4, provide the inputs. The output has 1s in three of eight positions, meaning that it represents a value of 3/8—the product of the two inputs.
Engineers welcomed stochastic computing when it was first developed in the 1960s because it allowed them to perform complicated mathematical functions with just a few transistors or logic gates, which at the time were rather costly. But transistors soon became much cheaper to make, and the attraction of stochastic computing quickly faded, as did solutions that involved just analog circuitry. The now-common forms of digital circuitry took off because they offered much better speed, performance, and flexibility.
But an important exception to that rule appeared in the mid-2000s, shortly after a new error-detection and error-correction scheme, low-density parity check (LDPC), started coming into widespread use. Discovered in the 1960s, LDPC codes are now used everywhere in communication systems, including Wi-Fi networks. Decoding LDPC codes can be a tricky business, however. But because the decoding involves probabilistic algorithms, it can be implemented using relatively simple stochastic computing circuits.
The success of stochastic circuits in that context, and the fact that controlling power use has now become one of the biggest challenges facing chip designers, prompted us and other researchers to revisit stochastic computing several years ago. We wanted to see what else it could do in the modern electronic era.
It turns out there is quite a lot. Apart from saving power, stochastic computing also offers a unique property known as progressive precision. That’s because, with this technique, the precision of the calculations depends on the length of the bitstream you use. For example, suppose you’re using 0110101010010111 to represent the fraction 9/16 (nine 1s in 16 possible bit positions). With stochastic computing, the leftmost digits are processed first, and all bits have equal significance or weight. If you look at the first eight bits of this example, 01101010, you get the number 4/8, which is a low-precision estimate of the value represented by the longer sequence.
The circuits that are used to process stochastic bitstreams act as though they are computing with the most significant digits of the number first. Conventional digital circuits—or paper-and-pencil calculations—work the other way, from the least to the most significant digits. When a normal computer adds two binary numbers together, the first bits computed don’t provide any sort of early approximation of the overall result.
Stochastic computing circuits, on the other hand, do exactly that: Their progressive-precision property means that the answer is pretty good at the start and tends to get increasingly precise as more and more bits flow through the circuit. So a computation can be ended as soon as enough bits have emerged in the results, leading to significant energy savings.
How many bits is enough? That depends on the application, and those that demand high precision will, of course, require longer bitstreams—perhaps hundreds or even thousands of bits.
There are limits to the precision you can achieve in practice, though. That’s because to represent an n-bit binary number, stochastic computing requires the length of the bitstream to be at least 2 n . Take the case of 8-bit numbers, of which there are 256 possible values. Suppose you wanted to represent the probability 1/256 with a bitstream. You’d need a bitstream that is at the very least 256 bits long—otherwise there wouldn’t be a place for a lone 1 in a sea of 0s. Similarly, to represent 9-bit numbers, you’d need streams of at least 512 bits. For 10-bit numbers, the requirement would be for 1,024 bits, and so on. Clearly, the numbers get large fast. Achieving even what is known in computer programming circles as single precision (32 bits) would be nearly impossible, because it would require streams of billions of bits to be manipulated.
Illustration: David Schneider and Mark Montgomery
Bitstream Brains: Neural signals resemble bitstreams in that frequent spikes indicate high values of neural activity, just as frequent 1s in a bitstream indicate high values for the number that it represents.
Low in precision as it is, stochastic computing is curiously similar to what goes on inside our brains. Our neural pathways encode their signals primarily by the rate or frequency of sharp electrical pulses or “spikes.” When those spikes are few and far between, the activity of the neural pathway is said to be low; when they occur frequently, the activity level is high. Similarly, when the 1s in a bitstream are few and far between, the stream corresponds to a low number; when they are common, it encodes a high number.
Also, stochastic computing circuits, like many biological systems, are resilient in the face of many kinds of disturbances. If, for example, a source of environmental noise causes some of the binary digits in a bitstream to flip, the number represented by that bitstream won’t change significantly: Often there will be as many 1s that change to 0s as there are 0s that change to 1s, so the noise will just average out over time.
These similarities with biological systems weren’t lost on us when we began our research. And we had them in mind when we began looking into an exciting new application for stochastic computing—processing signals in retinal implants.
Retinal implants are intended to restore sight to people with severe macular degeneration, retinitis pigmentosa, and other degenerative diseases of the retina. Although using electronics to restore lost vision is an old idea, the actual clinical use of retinal implants is less than a decade old, and it’s been attempted with comparatively few patients because the technology remains so rudimentary.
Most retinal implants capture and process images outside the eye using a camera and a digital computer. That’s pretty clunky. And it gives patients an odd sense when they move their eyes and find that the image projected on their retinas doesn’t move in the way their brains expect. What you really want, of course, is for the image sensing and processing to take place inside the eye. One hurdle to accomplishing this is that there’s little power available inside the eye to operate the electronics—the only power sources available are tiny inductive pick-up coils or photovoltaic cells. And you need relatively large amounts of power to sense and process images using conventional digital circuits. Even if a source of sufficient power were available, using it would still be problematic because excessive power dissipation can harm eye tissues, which can tolerate only a few degrees of temperature rise.
For these reasons, we figured that the simplicity and efficiency of stochastic computing could make a big difference. To test this idea, we conducted a little experiment. We designed several stochastic image-processing circuits, including one that detects edges in images. (Edge detection improves contrast, making objects easier to perceive.) Not surprisingly, the stochastic circuit we designed for this purpose is much simpler and more efficient in its use of power than the kinds of digital circuits typically used for edge detection.
Another biologically inspired application of stochastic computing is in artificial neural networks, which lie at the heart of many of today’s smart systems. We explored this application recently using an image sensor connected to such a neural network, one configured to recognize digits after it has been trained to do so—meaning that its many adjustable parameters have been set at values that allow it to classify the images presented to it as a specific digit. Neural networks are arranged in a series of layers of artificial neurons, where the output of one layer serves as the input to the next. In our experiments, we replaced the first processing layer of our network with stochastic circuitry.
Although the stochastic circuitry sometimes gave inaccurate arithmetic results, it did not matter because neural networks can learn to tolerate such errors. So we just retrained our neural network to deal with the stochastic errors. In this way, we could reduce the energy used in the first layer of the network by a factor of 10, while pretty much preserving the original level of accuracy in digit classification.
Image: Armin Alaghi
Always on Edge: Edge detection is commonly used in image processing. Here, an edge-detection algorithm that uses conventional binary numbers [top row] is compared with one that uses stochastic bitstreams [bottom row]. The stochastic results hold up much better as the bit-error rate is increased from 0.1 percent [far left] to 0.5 percent [middle left] to 1.0 percent [middle right] and finally to 2.0 percent [far right].
One of the things holding stochastic computing back has been the lack of any comprehensive design methodology. Sure, it’s easy enough to design circuits for simple arithmetic operations such as multiplication and addition, but when the target function is more complicated, engineers have long been without a good road map.
A decade ago, Weikang Qian and Marc Riedel, of the University of Minnesota, devised a novel technique to solve this problem. Building on their work, we recently discovered another approach to designing stochastic computing circuits. It begins with the observation that a stochastic circuit corresponds to a Boolean function. AND, OR, NAND, and NOR are all examples of Boolean functions. More generally, they are defined as a mathematical function that takes some number of different inputs (each of which can be 0 or 1) and produces one output, which, depending on the input values, will be 0 or 1.
Suitable mathematical transformations applied to that Boolean function—ones similar to those used to determine, for example, the frequency content of audio signals—reveal how the stochastic circuit will operate on bitstreams, whether it will serve as a multiplier, say, or an adder. We found that you can go the other way, too. You can start with the desired function and perform those mathematical transformations in reverse to deduce the circuit needed.
Based on that observation, we developed a method that enabled us to design efficient stochastic computing circuits for image processing, including one that could carry out a common image-processing function called gamma correction. (Gamma correction is used to account for the insensitivity of the human eye to small differences in brightness in lighter areas of an image.) With this strategy, we were able to design a small (eight gate) circuit that implements the gamma-correction function.
Efficient as they are, stochastic circuits can be made even more so when combined with a power-reduction technique known as voltage scaling. That’s basically a highfalutin way of saying that you dial the voltage way down to save energy at the cost of creating occasional errors. That’s not much of a problem for stochastic circuits, which can work acceptably well at voltages that would be too low for conventional ones. For example, the gamma-correction circuit we built can tolerate a voltage reduction up to 40 percent, from 1 volt down to 0.6 V, with no loss of accuracy. And unlike conventional binary circuits, which fail catastrophically when the voltage scaling is too aggressive, stochastic circuits continue to operate, albeit with less precision, as the voltage is reduced.
While our examination of circuits for retinal implants and neural networks makes us very optimistic about the prospects for stochastic computing, we still haven’t discovered the real killer app for this approach. It may be 50 years old, but stochastic computing, in our view, is still in its infancy.
This article appears in the March 2018 print issue as “Computing With Randomness.”
About the Authors
Armin Alaghi works at Oculus Research and is a research associate at the University of Washington. John P. Hayes is the Claude E. Shannon Professor of Engineering Science at the University of Michigan.
Computing With Random Pulses Promises to Simplify Circuitry and Save Power syndicated from https://jiohowweb.blogspot.com
0 notes