#dfs example in directed graph | Explore Tumblr posts and blogs

eatsleepmath · 7 years ago

Text

Strong conceptual completeness for $\aleph_0$-categorical theories, 2:

This series of posts is a serialization of (what started as) notes for a talk I gave at the Harvard logic seminar on 6 February 2018. You can view them in order here.

Pre-ultrafunctors

When $X : \operatorname{\mathbf{Mod}}(T) \to \mathbf{Set}$ is $\operatorname{ev}_{\varphi(x)}$ and one proves the Łos theorem \[X\left(\prod_{i \to \mathcal{U}} M_i \right) = \prod_{i \to \mathcal{U}} X(M_i),\] one has the luxury of being able to test the displayed equation above between two subsets of (the interpretation in $\prod_{i \to \mathcal{U}} M_i$ of) the ambient sort of the formula $\varphi(x)$. If $X$ is merely isomorphic to $\operatorname{ev}_{\varphi(x)}$, then $X\left(\prod_{i \to \mathcal{U}} M_i\right)$ and $\prod_{i \to \mathcal{U}} X(M_i)$ might be entirely different sets, with only the isomorphism to $\operatorname{ev}_{\varphi(x)}$ to compare them, so that testing equality as above is not a well-formulated question; rather, one asks for an isomorphism.

Remark. Given a natural isomorphism $\eta : X \simeq \operatorname{ev}_{\varphi(x)}$ with components $\{\eta_{M} : X(M) \simeq \varphi(M)\}_{M \in \operatorname{\mathbf{Mod}}(T)}$, we have for every ultraproduct $\prod_{i \to \mathcal{U}} M_i$ a commutative square

where the dashed map $\Phi_{(M_i)}$ is the composition of isomorphisms $\left(\prod_{i \to \mathcal{U}} \eta_{M_i} \right)^{-1} \circ \eta_{\prod_{i \to \mathcal{U}} M_i}$.

It is easy to see that the statement of Łos’ theorem is functorial on elementary embeddings. That is, for every $I$, every ultrafilter $\mathcal{U}$ on $I$, and every sequence of elementary embeddings $f_i : M_i \to N_i$, the diagram

commutes.

Definition. For an arbitrary functor $X : \operatorname{\mathbf{Mod}}(T) \to \mathbf{Set}$, if we additionally specify for every $I, \mathcal{U}, (M_i)_{i \in I}$ the data of a transition isomorphism $\Phi_{(M_i)} : X\left(\prod_{i \to \mathcal{U}} M_i\right) \to \prod_{i \to \mathcal{U}} X(M_i)$, then we say that $(X, \Phi)$ “commutes with ultraproducts” if all diagrams

commute. We let $\Phi$ abbreviate all the transition isomorphisms, and we call a pair $(X,\Phi)$ a pre-ultrafunctor. We will abuse terminology by referring to $\Phi$ as “the” transition isomorphism of the pre-ultrafunctor $(X, \Phi)$.

Given two pre-ultrafunctors $(X, \Phi)$ and $(X', \Phi')$, we define a map between them, called an ultratransformation, to be a natural transformation $\eta : X \to X'$ which satisfies the following additional property: all diagrams

must commute.

With this terminology, the theorem says that if $X$ is a sub-pre-ultrafunctor of an evaluation functor $\operatorname{ev}_{\varphi(x)}$, then $X$ is definable.

In light of the above definition, we can reformulate our observation about a definable functor $X \overset{\eta}{\simeq} \operatorname{ev}_{\varphi(x)}$ above as saying that the natural isomorphism $\eta$ canonically equips $X$ with a transition isomorphism such that $\eta$ is an ultratransformation.

Remark. Every functor of points $\operatorname{ev}_{\varphi(x)}$ can be canonically viewed as a pre-ultrafunctor with the transition isomorphisms $\Phi$ just the identity maps (corresponding to the equality signs in the above diagrams).

One checks that if $X$ and $Y$ are definable sets, and $f : X \to Y$ is a definable function, then the induced natural transformation between evaluation functors $\operatorname{ev}_f : ev_X \to \operatorname{ev}_Y$ is in fact an ultratransformation. (This contains Los’ theorem: in the proof, one is really showing that if $S$ is the sort containing a formula $\varphi(x)$, then the canonical definable injection $i : \varphi(x) \hookrightarrow S$ induces an ultratransformation; the fact that the transition isomorphisms are all identities means that one ends up with the usual equality.)

Definition. The category of pre-ultrafunctors $\mathbf{PUlt}(\operatorname{\mathbf{Mod}}(T), \mathbf{Set})$ comprises objects preultrafunctors $(X, \Phi)$ and morphisms the ultratransformations.

Remark. By the remark, the evaluation functor $\operatorname{ev} : \operatorname{\mathbf{Def}}(T) \to [\operatorname{\mathbf{Mod}}(T), \mathbf{Set}]$ further factors through $\mathbf{PUlt}(\operatorname{\mathbf{Mod}}(T), \mathbf{Set})$:

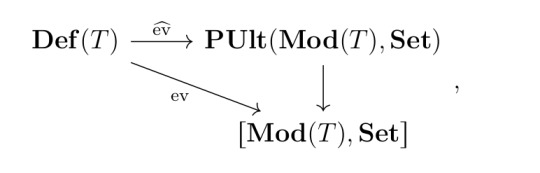
where the arrow $\mathbf{PUlt}(\operatorname{\mathbf{Mod}}(T), \mathbf{Set})$ is just the forgetful functor $(X, \Phi) \mapsto X$.

Note that whenever there is an isomorphism $\eta : X \simeq Y$ as functors $\operatorname{\mathbf{Mod}}(T) \to \mathbf{Set}$, and $(X, \Phi)$ is a pre-ultrafunctor, then by conjugating $\Phi$ by the isomorphism $X \simeq Y$ (as in the diagram), one canonically equips $Y$ with a transition isomorphism $\Phi'$ such that $\eta : (X, \Phi) \to (Y, \Phi')$ is an ultratransformation.

Remark. That is, $X$ is definable if and only if there is a transition isomorphism $\Phi$ such that $(X,\Phi)$ is isomorphic to $(\operatorname{ev}_{\varphi(x)}, \operatorname{id})$ for some formula $\varphi(x) \in T$. We will suppress the canonical transition isomorphism $\operatorname{id}$ and just say that $(X,\Phi)$ is isomorphic to $\operatorname{ev}_{\varphi(x)}$, understanding that this isomorphism is happening in $\mathbf{PUlt}(\operatorname{\mathbf{Mod}}(T), \mathbf{Set})$.

The pre-ultrafunctor condition only stipulates compatibility with respect to ultraproducts of elementary embeddings. However, there are other elementary embeddings which arise purely formally between different ultraproducts with respect to different indexing sets and ultrafilters, and should be viewed as part of the formal structure on $\operatorname{\mathbf{Mod}}(T)$ which is induced by being able to take ultraproducts. The canonical example is the diagonal embedding of a model into its ultrapower (which compares an ultrapower $M$ with respect to the trivial indexing set and trivial ultrafilter to an ultrapower $M^{\mathcal{U}}$ with respect to a nontrivial indexing set and a nontrivial ultrafilter).

Definition. Fix $I$, $\mathcal{U}$, and a model $M \models T$.

The diagonal embedding $\Delta_M : M \to M^{\mathcal{U}}$ is given by sending each $a \in M$ to the equivalence class of the constant sequence $[a]_{i \to \mathcal{U}}$.

We can stipulate that a pre-ultrafunctor furthermore preserves the diagonal embeddings.

Definition. We say that a pre-ultrafunctor $(X,\Phi)$ is a $\Delta$-functor if for every $I$, for every $\mathcal{U}$, and for every $M$ and the diagonal embedding $M \overset{\Delta_M}{\longrightarrow} M^{\mathcal{U}}$, the diagram

commutes.

Remark. It is not true in general that the embedding $\widehat{\operatorname{ev}} : \operatorname{\mathbf{Def}}(T) \to \mathbf{PUlt}(\operatorname{\mathbf{Mod}}(T), \mathbf{Set})$ is an equivalence of categories. If $(X, \Phi)$ is isomorphic to $\operatorname{ev}_{\varphi(x)}$, then $(X, \Phi)$ preserves the diagonal embeddings of models into their ultrapowers (in the sense of the definition). However, later, we will exhibit an example of a pre-ultrafunctor which does not preserve diagonal embeddings.

It is not true either that in general being a $\Delta$-functor characterizes the image of $\widehat{\operatorname{ev}}$; we later construct a counterexample.

Strong conceptual completeness says that if we sufficiently generalize the diagonal embeddings to a large-enough class of formal comparison maps between ultraproducts (with respect to possibly different indexing sets and ultrafilters), then we can characterize the image of $\widehat{\operatorname{ev}}$ as precisely those pre-ultrafunctors which additionally preserve all these formal comparison maps. The notion we want is that of an ultramorphism.

Ultramorphisms

Definition. An ultragraph $\Gamma$ comprises:

Two disjoint sets $\Gamma^f$ and $\Gamma^b$, called the sets of free nodes and bound nodes, respectively.

For any pair $\gamma, \gamma' \in \Gamma$, there exists a set $E(\gamma, \gamma')$ of edges. This gives the data of a directed graph.

For any bound node $\beta \in \Gamma^b$, we assign a triple $\langle I, \mathcal{U}, g \rangle \overset{\operatorname{df}}{=} \langle I_{\beta}, \mathcal{U}_{\beta}, g_{\beta} \rangle$ where $\mathcal{U}$ is an ultrafilter on $I$ and $g$ is a function $g : I \to \Gamma^f$.

Definition. An ultradiagram of type $\Gamma$ in a pre-ultracategory $\underline{\mathbf{S}}$ is a diagram $A : \Gamma \to \mathbf{S}$ assigning an object $A$ to each node $\gamma \in X$, and assigning a morphism in $\mathbf{S}$ to each edge $e \in E(\gamma, \gamma')$, such that \[\label{eqn-ultradiagram-condition} A(\beta) = \prod_{i \in I_{\beta}} A(g_{\beta}(i))/\mathcal{U}_{\beta}\] for all bound nodes $\beta \in \Gamma^b$.

Given this notion of a diagram with extra structure, there is an obvious notion of natural transformations between such diagrams which preserve the extra given structure.

Definition. Let $A, B : \Gamma \to \mathbf{S}$. A morphism of ultradiagrams $\Phi : A \to B$ is a natural transformation $\Phi$ satisfying \[\label{eqn-ultradiagram-morphism-condition} \Phi_{\beta} = \prod_{i \to \mathcal{U}_{\beta}} \Phi_{g_{\beta}(i)}\] for all bound nodes $\beta \in \Gamma^b$.

Now we define ultramorphisms.

Definition. Let $\operatorname{Hom}(\Gamma, \underline{\mathbf{S}})$ be the category of all ultradiagrams of type $\Gamma$ inside $\underline{\mathbf{S}}$ with morphisms the ultradiagram morphisms defined above. Any two nodes $k, \ell \in \Gamma$ define evaluation functors $(k), (\ell) : \operatorname{Hom}(\Gamma, \underline{\mathbf{S}}) \rightrightarrows \mathbf{S},$ by \[(k) \left(A \overset{\Phi}{\to} B \right) = A(k) \overset{\Phi_k}{\to} B(k)\] (resp. $\ell$).

An ultramorphism of type $\langle \Gamma, k, \ell \rangle$ in $\underline{\mathbf{S}}$ is a natural transformation $\delta : (k) \to (\ell)$.

Let us unravel the definition for the prototypical example $\Delta : M \hookrightarrow M^{\mathcal{U}}$ of an ultramorphism.

Example. Given an ultrafilter $\mathcal{U}$ on $I$, put:

$\Gamma^f = \{k\}$,

$\Gamma^b = \{\ell\}$,

$E(\gamma, \gamma') = \emptyset$ for all $\gamma, \gamma' \in \Gamma$,

$\langle I_{\ell}, \mathcal{U}_{\ell}, g_{\ell} \rangle = \langle I, \mathcal{U}, g \rangle$ where $g$ is the constant map to $k$ from $I$.

By the ultradiagram condition, an ultradiagram $A$ of type $\Gamma$ in $\underline{\mathbf{S}}$ is determined by $A(k)$, with $A(\ell) = A(k)^{\mathcal{U}}$.

By the ultradiagram morphism condition, an ultramorphism of type $\langle \Gamma, k, \ell \rangle$ must be a collection of maps $\left(\delta_M : M \to M^{\mathcal{U}} \right)_{M \in \operatorname{\mathbf{Mod}}(T)}$ which make all squares of the form

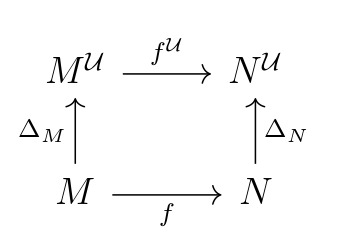
commute. It is easy to check that setting $\delta_M = \Delta_M$ the diagonal embedding gives an ultramorphism.

Definition. The next least complicated example of an ultramorphism are the generalized diagonal embeddings. Here is how they arise: let $g : I \to J$ be a function between two indexing sets $I$ and $J$. $g$ induces a pushforward map $g_* : \beta I \to \beta J$ between the spaces of ultrafilters on $I$ and $J$, by $g_* \mathcal{U} \overset{\operatorname{df}}{=} \{P \subseteq J \operatorname{\big{|}} g^{-1}(P) \in \mathcal{U}$. Fix $\mathcal{U} \in \beta I$ and put $\mathcal{V} \overset{\operatorname{df}}{=} g_* \mathcal{U}$. Let $(M_j)_{j \in J}$ be a $J$-indexed family of models.

Then there is a canonical “fiberwise diagonal embedding” \[\Delta_g : \prod_{j \to \mathcal{V}} M_j \to \prod_{i \to \mathcal{U}} M_{g(i)}\] given on $[a_j]_{j \to \mathcal{V}}$ by replacing each entry $a_j$ with $g^{-1}(\{a_j\})$-many copies of itself.

In terms of the definition of an ultramorphism, the free nodes are $J$, and there are two bound nodes $k$ and $\ell$. To $k$ we assign the triple $\langle J, \mathcal{V}, \operatorname{id}_J \rangle$ and to $\ell$ we assign the triple $\langle I, \mathcal{U}, g \rangle$. Then $\Delta_g$ induces an ultramorphism $(k) \to (\ell)$.

Now we state what it means for ultramorphisms to be preserved. One should keep in mind the special case of the diagonal ultramorphism.

Definition. Let $(X,\Phi) : \operatorname{\mathbf{Mod}}(T) \to \mathbf{Set}$ be a pre-ultrafunctor, and let $\delta$ be an ultramorphism in $\operatorname{\mathbf{Mod}}(T)$ and $\delta'$ an ultramorphism in $\mathbf{Set}$, both of ultramorphism type $\langle \Gamma, k, \ell \rangle$

Recall that in the terminology of the definition, $\delta$ is a natural transformation $(k) \overset{\delta}{\to} (\ell)$ of the evaluation functors \[(k), (\ell) : \operatorname{Hom}(\Gamma, \operatorname{\mathbf{Mod}}(T)) \to \operatorname{\mathbf{Mod}}(T).\] (Resp. $\delta'$, $\mathbf{Set}$.)

Note that for any ultradiagram $\mathscr{M} \in \operatorname{Hom}(\Gamma, \operatorname{\mathbf{Mod}}(T))$, $X \circ \mathscr{M}$ is an ultradiagram in $\operatorname{Hom}(\Gamma, \mathbf{Set})$. We say that $X$ carries $\delta$ into $\delta'$ (prototypically, $\delta$ and $\delta'$ will both be canonically defined in the same way in both $\operatorname{\mathbf{Mod}}(T)$ and $\mathbf{Set}$ and in this case we say that $\delta$ has been preserved) if for every ultradiagram $\mathscr{M} \in \operatorname{Hom}(\Gamma, \operatorname{\mathbf{Mod}}(T))$, the diagram

commutes. (We are abusing notation and understand that in the above if $k$ is not a bound node, then the ultraproduct on the bottom left becomes trivial and $\Phi_{\mathscr{M}(k)}$ is actually the identity map $\operatorname{id}_{X(\mathscr{M}(k))}$ (resp. $\ell$, ultraproduct on the bottom right).)

Note that what is really happening is that we are applying the covariant Hom-functor $\operatorname{Hom}(X,-)$ to push forward each ultradiagram $\mathscr{M}$ to an ultradiagram $X \circ \mathscr{M}$, and then asking that the pushed-forward ultramorphism $X(\delta)$ is isomorphic to $\delta'_{X \mathscr{M}}$ via $X$’s transition isomorphism $\Phi$.

Stating strong conceptual completeness

Just as $\Delta$-functors are pre-ultrafunctors which additionally preserve the diagonal embedding ultramorphisms, we define ultrafunctors to be pre-ultrafunctors which preserve all ultramorphisms.

Definition. An ultrafunctor $X : \operatorname{\mathbf{Mod}}(T) \to \mathbf{Set}$ is a pre-ultrafunctor which respects the fibering over $\mathbf{Set}$: for every $\delta \in \Delta(\mathbf{Set})$, $X$ carries $\delta_{\operatorname{\mathbf{Mod}}(T)}$ into $\delta_{\mathbf{Set}}$ (in the sense of the definition above) for all $\delta \in \Delta(\mathbf{Set})$.

Definition. A map between ultrafunctors is just an ultratransformation of the underlying pre-ultrafunctors. Write $\mathbf{Ult}(\operatorname{\mathbf{Mod}}(T), \mathbf{Set})$ for the category of ultrafunctors $\operatorname{\mathbf{Mod}}(T) \to \mathbf{Set}$.

There is a canonical evaluation functor \[\widetilde{\operatorname{ev}} : \operatorname{\mathbf{Def}}(T) \to \mathbf{Ult}(\operatorname{\mathbf{Mod}}(T), \mathbf{Set})\] sending each definable set $A \in T$ to its corresponding ultrafunctor $\widetilde{\operatorname{ev}}_A$, and we now have the following picture of factorizations of the original evaluation map $\operatorname{ev} : \operatorname{\mathbf{Def}}(T) \to [\operatorname{\mathbf{Mod}}(T) \to \mathbf{Set}]$:

Now, we can state strong conceptual completeness.

Theorem. The functor $\widetilde{\operatorname{ev}} : \operatorname{\mathbf{Def}}(T) \to \mathbf{Ult}(\operatorname{\mathbf{Mod}}(T), \mathbf{Set})$ is an equivalence of categories.

#math #model theory #strong conceptual completeness

22 notes · View notes

billypeterson449 · 3 years ago

Text

Introduction To Recursion In C++

To begin with recursion in C++, we must first understand the fundamental concept of C++ functions, which comprises function definitions that call other functions. Also covered in this article is the concept of the recursive definition, a math and programming logic play tool. A common example is the factorial of a number, the sum of "n" natural numbers, and so on. The term "recursive function" refers to a function that calls itself. They are simply a function that is called repeatedly. Recursion offers a problem-solving tool that separates huge problems into simple tasks that are worked out separately in a sequential order.

The recursive function is used to solve problems in data structures such as searching, sorting, and tree traversal. This programming method makes it easy to write code. Iteration and recursion both repeat the code, but recursion executes a specific part of the code with the base function itself. In this article, we will go over the importance of recursion and how it works.

What Is Recursion?

Recursion is the process of a function calling itself as a subroutine to tackle a complex iterative task by breaking it down into smaller chunks. Recursive functions are those that call themselves recursively, while recursion is the process of invoking a function by itself. Recursion results in a large number of iterative calls to the same function; however, a base case is required to end the recursion.

By dividing a complex mathematical computation task into subtasks, recursion is an efficient way to solve it. Divide and Conquer is the name for this method of problem-solving. It allows programmers to break down a complex problem into smaller tasks and solve them one at a time to arrive at a final solution.

Any problem that can be solved recursively can also be solved iteratively, but recursion is the more efficient method of programming because it uses the least amount of code to accomplish the same complex task. Although recursion is not suitable for all problems, it is particularly well suited for sorting, searching, Inorder/Preorder/Postorder Tree Traversals, and DFS of Graph algorithms. Recursion, on the other hand, must be implemented with care; otherwise, if no base condition is met to terminate the function, it may result in an infinite loop.

How Recursive Functions Work In C++?

When the base case is true, recursion conducts repetition on the function calls and stops the execution. To avoid the stack overflow error message, a base case condition should be defined in the recursive code. Infinite recursion results if no base case is defined. When a function is called, it is pushed into a stack each time so that resources can be reserved for subsequent calls. It is the most effective at traversing trees. Direct and indirect recursion are two separate forms of recursion.

Direct Recursion: A direct recursive function is one that calls itself directly, and this sort of recursion is known as direct recursion.

Indirect Recursion : When a function calls itself indirectly from another function, it is referred to as indirect recursive, and this sort of recursion is referred to as indirect recursion.

Memory Allocation In Recursion:

Memory allocation for recursive functions is similar to memory allocation for other functions. A single memory block in a stack is allocated when a recursive function is called. This memory block provides the necessary memory space for the function's successful execution as well as the storage of all local, automatic, and temporary variables. It pushes a separate stack frame for each recursive call in the same way. There will be 5 stack frames corresponding to each recursive call if a recursive function is called 5 times. When the recursive call is completed, the new stack frame is discarded, and the function begins to return its value to the function in the previous stack frame. The stack is then popped out in the same order that it was pushed, and memory is deallocated. The final result value is returned at the end of the recursion, and the stack is destroyed and memory is freed up. The stack will quickly be depleted if the recursion fails to reach a base case, resulting in a Stack Overflow crash.

Advantages Of Recursion:

They create clean and compact code by simplifying a larger, more complex application.

In the computer code, there are fewer variables.

Here, nested for loops and complex code are avoided.

Backtracking is required in several parts of the code, which is solved recursively.

Disadvantages Of Recursion:

Due to the stack operation of all the function calls, it requires extra memory allocation.

When doing the iteration process, it can be a little sluggish at times. As a result, efficiency suffers.

Beginners may find it challenging to comprehend the workings of the code because it can be quite complex at times. If this happens, the software will run out of memory and crash.

Summary:

We've talked about how functions operate and defined them in a recursive manner. We've also gone over the correspondence and the benefits and drawbacks of recursive functions in programming.

#Recursion In C++#recursive function in c++

0 notes

waitarajo-blog · 4 years ago

Text

Exploring Statistical Interactions

Table of TAB12MDX by USQUAN

TAB12MDX(Tobacco Dependence Past 12 Months)

USQUAN

Frequency Percent Row Pct Col Pct

Total

0630 50.00 91.84 52.72

56 4.44 8.16 86.15

686 54.44

565 44.84 98.43 47.28

9 0.71 1.57 13.85

574 45.56

Total

1195 94.84

65 5.16

1260 100.00

Statistics for Table of TAB12MDX by USQUAN

Statistic

Value

Prob

Chi-Square

27.7842

<.0001

Likelihood Ratio Chi-Square

31.3968

<.0001

Continuity Adj. Chi-Square

26.4525

<.0001

Mantel-Haenszel Chi-Square

27.7621

<.0001

Phi Coefficient

-0.1485

Contingency Coefficient

0.1469

Cramer's V

-0.1485

Fisher's Exact Test

Cell (1,1) Frequency (F)

630

Left-sided Pr <= F

<.0001

Right-sided Pr >= F

1.0000

Table Probability (P)

<.0001

Two-sided Pr <= P

<.0001

Sample Size = 1260

Table of TAB12MDX by USQUAN

TAB12MDX(Tobacco Dependence Past 12 Months)

USQUAN

Frequency Percent Row Pct Col Pct

Total

0110 24.66 88.71 25.70

14 3.14 11.29 77.78

124 27.80

318 71.30 98.76 74.30

4 0.90 1.24 22.22

322 72.20

Total

428 95.96

18 4.04

446 100.00

Statistics for Table of TAB12MDX by USQUAN

Statistic

Value

Prob

Chi-Square

23.3380

<.0001

Likelihood Ratio Chi-Square

20.3350

<.0001

Continuity Adj. Chi-Square

20.8157

<.0001

Mantel-Haenszel Chi-Square

23.2856

<.0001

Phi Coefficient

-0.2288

Contingency Coefficient

0.2230

Cramer's V

-0.2288

Fisher's Exact Test

Cell (1,1) Frequency (F)

110

Left-sided Pr <= F

<.0001

Right-sided Pr >= F

1.0000

Table Probability (P)

<.0001

Two-sided Pr <= P

<.0001

Sample Size = 446

2 Variables:

urbanrate internetuserate

Simple Statistics

Variable

Mean

Std Dev

Sum

Minimum

Maximum

Label

urbanrate

33.50553

12.83453

1575

10.40000

66.60000

urbanrate

internetuserate

8.22063

8.70764

369.92856

0.21007

40.12223

INTERNETUSERATE

Pearson Correlation Coefficients Prob > |r| under H0: Rho=0 Number of Observations

urbanrate

internetuserate

urbanrate urbanrate

1.00000 47

0.11558 0.4496 45

internetuserate INTERNETUSERATE

0.11558 0.4496 45

1.00000 45

2 Variables:

urbanrate internetuserate

Simple Statistics

Variable

Mean

Std Dev

Sum

Minimum

Maximum

Label

urbanrate

56.58000

18.64588

5319

12.54000

93.32000

urbanrate

internetuserate

30.76527

19.76304

2830

1.28005

79.88978

INTERNETUSERATE

Pearson Correlation Coefficients Prob > |r| under H0: Rho=0 Number of Observations

urbanrate

internetuserate

urbanrate urbanrate

1.00000 94

0.32516 0.0017 91

internetuserate INTERNETUSERATE

0.32516 0.0017 91

1.00000 92

2 Variables:

urbanrate internetuserate

Simple Statistics

Variable

Mean

Std Dev

Sum

Minimum

Maximum

Label

urbanrate

78.20417

19.82159

3754

13.22000

100.00000

urbanrate

internetuserate

70.58821

15.94746

3247

36.00033

95.63811

INTERNETUSERATE

Pearson Correlation Coefficients Prob > |r| under H0: Rho=0 Number of Observations

urbanrate

internetuserate

urbanrate urbanrate

1.00000 48

0.07514 0.6197 46

internetuserate INTERNETUSERATE

0.07514 0.6197 46

1.00000 46

Now, let's evaluate third variables as

potential moderators in the context of chi-squared test of independence. For this, we're gonna return to our

original SAS program using the NESARC data and asking the question, is smoking

associated with nicotine dependence? We're going to create another

smoking variable for this purpose, reflecting how many cigarettes each

young adult smoker smokes per day. 0 will indicate non-daily smokers. 3 indicates those smoking

1 to 5 cigarettes per day. 8 indicates 6 to 10 cigarettes per day. 13 indicates 11 to 15 cigarettes per day. 18 indicates 16 to 20 cigarettes per day,

and 37 indicates greater than

20 cigarettes per day.Categorical explanatory variable

USQUAN/discrete tells SAS that we want levels of our categorical explanatory

variable to be represented on the x-axis.

TAB12MDX to be displayed as a mean on the y-axis. And this gives us the graphic

representation of this positive linear relationship. As smoking quantity increases, so does the proportion of individuals

with nicotine dependence. This finding is accurate with regard

to the larger population of young adult smokers. Though might a third variable

moderate the relationship between smoking quantity and nicotine? Put another way,

might there be a statistical interaction between a third

variable in smoking behavior and predicting our response variable,

nicotine dependence? We're going to evaluate major depressive

disorder as the third variable. Our question will be, does Major

Depression affect either the strength or the direction of the relationship

between smoking and nicotine dependence? Put another way, might a third

variable moderate the relationship between smoking and nicotine dependence? Is smoking related to nicotine dependence

for each level of this third variable, that is, for those with major depression

and those without major depression? Similar to our anova example, syntax to be added to the PROC FREQ

code is circled here in red. We need to first sort the data, according

to the categorical third variable, then include a bistatement,

telling SAS to run a chi-square for each level of the third

variable separately. The specific syntax for this example is shown here, PROC SORT; BY MAJORDEPLIFE;

PROC FREQ; TABLES TAB12MDX*USQUAN/CHISQ; BY MAJORDEPLIFE;. When this syntax is added to the SAS

program, here are the results. You can see the cross tabs or

cross tabulation table, looking at usual quantity by tobacco

dependence in the past 12 months. First, for major depression equal to 0,

which is those without major depression, the chi-square value is large and

the P-value is quite small. In addition, the column percents

reveal what seems to be a positive linear relationship with percentages

of nicotine dependency increasing between lower levels of smoking and

higher levels of smoking. So we can say that this is a statistically

significant relationship for those without major depression. For those with major depression,

we find a large chi-square value and small P value,

which is statistically significant. These column percents also reveal what

seems to be a positive linear relationship with percentages of nicotine

dependence increasing between lower levels of smoking and

higher levels of smoking. Using a line graph to examine the rates of

nicotine dependence by different levels of smoking, it seems that

both the direction and size of the relationship is

similar between smoking and nicotine dependence for those with

major depression and for those without. Although, those with major depression show

higher rates of nicotine dependence at every level of smoking quantity. In this case, we would say a diagnosis

of major depression does not moderate the relationship between smoking and

nicotine dependence. For both young adult smokers with major

depression and those without, higher levels of smoking behavior is associated

with higher rates of nicotine dependence.

0 notes

holytheoristtastemaker · 5 years ago

Link

Have you ever solved a real-life maze? The approach that most of us take while solving a maze is that we follow a path until we reach a dead end, and then backtrack and retrace our steps to find another possible path. This is exactly the analogy of Depth First Search (DFS). It's a popular graph traversal algorithm that starts at the root node, and travels as far as it can down a given branch, then backtracks until it finds another unexplored path to explore. This approach is continued until all the nodes of the graph have been visited. In today’s tutorial, we are going to discover a DFS pattern that will be used to solve some of the important tree and graph questions for your next Tech Giant Interview! We will solve some Medium and Hard Leetcode problems using the same common technique. So, let’s get started, shall we?

Implementation

Since DFS has a recursive nature, it can be implemented using a stack. DFS Magic Spell:

Push a node to the stack

Pop the node

Retrieve unvisited neighbors of the removed node, push them to stack

Repeat steps 1, 2, and 3 as long as the stack is not empty

Graph Traversals

In general, there are 3 basic DFS traversals for binary trees:

Pre Order: Root, Left, Right OR Root, Right, Left

Post Order: Left, Right, Root OR Right, Left, Root

In order: Left, Root, Right OR Right, Root, Left

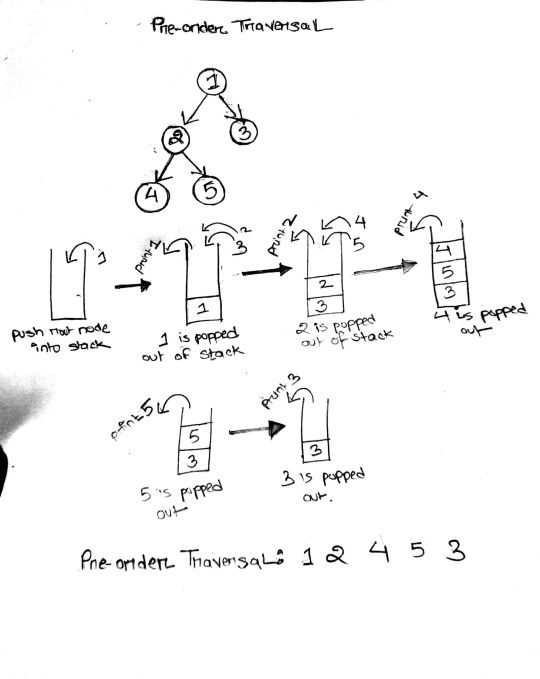
144. Binary Tree Preorder Traversal (Difficulty: Medium)

To solve this question all we need to do is simply recall our magic spell. Let's understand the simulation really well since this is the basic template we will be using to solve the rest of the problems.

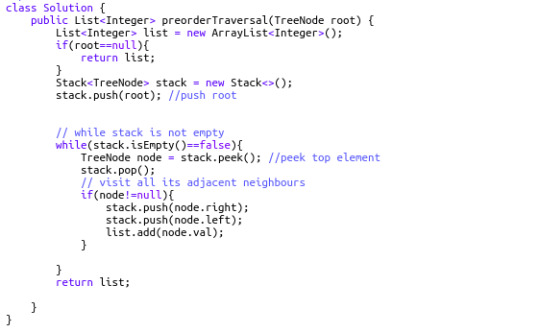
At first, we push the root node into the stack. While the stack is not empty, we pop it, and push its right and left child into the stack. As we pop the root node, we immediately put it into our result list. Thus, the first element in the result list is the root (hence the name, Pre-order). The next element to be popped from the stack will be the top element of the stack right now: the left child of root node. The process is continued in a similar manner until the whole graph has been traversed and all the node values of the binary tree enter into the resulting list.

145. Binary Tree Postorder Traversal (Difficulty: Hard)

Pre-order traversal is root-left-right, and post-order is right-left-root. This means post order traversal is exactly the reverse of pre-order traversal. So one solution that might come to mind right now is simply reversing the resulting array of pre-order traversal. But think about it – that would cost O(n) time complexity to reverse it. A smarter solution is to copy and paste the exact code of the pre-order traversal, but put the result at the top of the linked list (index 0) at each iteration. It takes constant time to add an element to the head of a linked list. Cool, right?

94. Binary Tree Inorder Traversal (Difficulty: Medium)

Our approach to solve this problem is similar to the previous problems. But here, we will visit everything on the left side of a node, print the node, and then visit everything on the right side of the node.

323. Number of Connected Components in an Undirected Graph (Difficulty: Medium)

Our approach here is to create a variable called ans that stores the number of connected components. First, we will initialize all vertices as unvisited. We will start from a node, and while carrying out DFS on that node (of course, using our magic spell), it will mark all the nodes connected to it as visited. The value of ans will be incremented by 1.

import java.util.ArrayList; import java.util.List; import java.util.Stack; public class NumberOfConnectedComponents { public static void main(String[] args){ int[][] edge = {{0,1}, {1,2},{3,4}}; int n = 5; System.out.println(connectedcount(n, edge)); } public static int connectedcount(int n, int[][] edges) { boolean[] visited = new boolean[n]; List[] adj = new List[n]; for(int i=0; i<adj.length; i++){ adj[i] = new ArrayList<Integer>(); } // create the adjacency list for(int[] e: edges){ int from = e[0]; int to = e[1]; adj[from].add(to); adj[to].add(from); } Stack<Integer> stack = new Stack<>(); int ans = 0; // ans = count of how many times DFS is carried out // this for loop through the entire graph for(int i = 0; i < n; i++){ // if a node is not visited if(!visited[i]){ ans++; //push it in the stack stack.push(i); while(!stack.empty()) { int current = stack.peek(); stack.pop(); //pop the node visited[current] = true; // mark the node as visited List<Integer> list1 = adj[current]; // push the connected components of the current node into stack for (int neighbours:list1) { if (!visited[neighbours]) { stack.push(neighbours); } } } } } return ans; } }

200. Number of Islands (Difficulty: Medium)

This falls under a general category of problems where we have to find the number of connected components, but the details are a bit tweaked. Instinctually, you might think that once we find a “1” we initiate a new component. We do a DFS from that cell in all 4 directions (up, down, right, left) and reach all 1’s connected to that cell. All these 1's connected to each other belong to the same group, and thus, our value of count is incremented by 1. We mark these cells of 1's as visited and move on to count other connected components.

547. Friend Circles (Difficulty: Medium)

This also follows the same concept as finding the number of connected components. In this question, we have an NxN matrix but only N friends in total. Edges are directly given via the cells so we have to traverse a row to get the neighbors for a specific "friend". Notice that here, we use the same stack pattern as our previous problems.

That's all for today! I hope this has helped you understand DFS better and that you have enjoyed the tutorial. Please recommend this post if you think it may be useful for someone else!

0 notes

oliverpdaniel · 4 years ago

Text

Advent of Code 2020: Reflection on Days 8-14

A really exciting week, with a good variety of challenges and relative difficulties. Something tells me that this year, being one where people are waking up later and staying at home all day, the problems have been specifically adapted to be more engaging and interesting to those of us working from home. Now that we've run the gamut of traditional AoC/competitve-programming challenges, I'm excited to see what the last 10 days have in store!

First things first, I have started posting my solutions to GitHub. I hope you find them useful, or at least not too nauseating to look at.

Day 8: To me, this is the quintessential AoC problem: you have a sequence of code-like instructions, along with some metadata the programmer has to keep track of, and there's some minor snit with the (usually non-deterministic) execution you have to identify. Some people in the subreddit feared this problem, thinking it a harbinger of Intcode 2.0. (Just look at that first line... somebody wasn't happy.)

Effectively, I got my struggles with this kind of problem out of the way several years ago: the first couple days of Intcode were my How I Learned to Stop Worrying and Love The While Loop, so this problem was a breeze. It also helps that I've been living and breathing assembly instructions these past few weeks, owing to a course project. I truly must learn, though, to start these problems after I finish my morning coffee, lest I wonder why my code was never executing the "jump" instruction...

Luckily, from here on out, there will be no more coffee-free mornings for me! Part of my partner's Christmas present this year was a proper coffee setup, so as to liberate them from the clutches of instant coffee. I'm not a coffee snob – or, at least, that's what I tell myself – but I was one more half-undrinkable cup of instant coffee away from madness.

Day 9: Bright-eyed, bushy-tailed, and full of fresh-ground and French-pressed coffee, I tackled today's problem on the sofa, between bites of a toasted homemade bagel.

This is a competitive programmer's problem. Or, at least, it would have been, if the dataset was a few orders of magnitude bigger. As of writing, every problem thus far has had even the most naïve solution, so long as it did not contain some massive bottleneck to performance, run in under a second. At first, I complained about this to my roommate, as I felt that the problem setters were being too lenient to solutions without any significant forethought or insight. But, after some thinking, I've changed my tune. Not everything in competitive programming[1] has to be punitive of imperfections in order to be enjoyable. The challenges so far have been fun and interesting, and getting the right answer is just as satisfying if you get it first try or fiftieth.

First off, if I really find myself languishing from boring data, I can always try to make the day more challenging by trying it in an unfamiliar language, or by microprofiling my code and trying to make it as efficient as possible. For example, I'm interested in finding a deterministic, graph theory-based solution to Day 7, such that I don't just search every kind of bag to see which kind leads to the target (i.e., brute-forcing). Maybe I'll give it a shot on the weekend, once MIPS and MARS is just a distant memory. A distant, horrible memory.

Second, even I – a grizzled, if not decorated, competitive and professional programming veteran – have been learning new concepts and facts about my own languages from these easy days. For example, did you know that set membership requests run in O(1) time in Python? That's crazy fast! And here I was, making dictionaries with values like {'a': True} just to check for visitation.

Part 1 was pretty pish-posh. Sure, in worst-case it ran in O(n^2), but when you have a constant search factor of 25 (and not, say, 10^25), that's really not a big deal.

Part 2 is what made me think that today's problem was made for competitive programmers. Whenever a problem mentions sums of contiguous subsets, my brain goes straight for the prefix sum array. They're dead simple to implement: I don't think I've so much as thought about PSAs in years, and I was able to throw mine together without blinking. I did have to use Google to jog my memory as to how to query for non-head values (i.e., looking at running sums not starting from index 0), but the fact that I knew that they could be queried that way at all probably saved me a lot of dev time. Overall complexity was O(nlogn) or thereabouts, and I'm sure that I could have done some strange dynamic programming limbo to determine the answer while I was constructing the PSA, but this is fine. I get the satisfaction of knowing to use a purpose-built data structure (the PSA), and of knowing that my solution probably runs a bit faster than the ultra-naive O(n^3)-type solutions that novice programmers might have come up with, even if both would dispatch the input quickly.

Faffing around on the AoC subreddit between classes, I found a lovely image that I think is going to occupy space in my head for a while. It's certainly easy to get stuck in the mindset of the first diagram, and it's important to centre myself and realize that the second is closer to reality.

Day 10: FML. Path-like problems like this are my bread and butter. Part 1 was easy enough: I found the key insight, that the values had to monotonically increase and thus the list ought to be sorted, pretty quickly, and the only implementation trick was keeping track of the different deltas.

Part 2, on the other hand, finally caught me on my Day 9 hubris: the naïve DFS, after ten minutes and chewing through all of my early-2014 MacBook's RAM, I still didn't have an answer. I tried being creative with optimizing call times; I considered using an adjacency matrix instead of a dictionary-based lookup; and I even considered switching to a recursion-first language like Haskell to boost performance. Ultimately, I stumbled onto the path of

spoilermemoization using `@functools.cache`

which frankly should have been my first bet. After some stupid typo problems (like, ahem, commenting out the function decorator), I was slightly embarrassed by just how instantly things ran after that.

As we enter the double-digits, my faith in the problem-setters has been duly restored: just a measly 108-line input was enough to trigger a Heat Death of the Universe execution time without some intelligent intervention. Well done, team!

Day 11: Good ol' Game of Life-style state transition problem. As per usual, I've sweated this type of problem out before, so for the actual implementation, I decided to go for Good Code as the real challenge. I ended up developing – and then refactoring – a single, pure state-transition function, which took in a current state, a neighbour-counting function, and a tolerance for the one element that changes between Parts 1 and 2 (you'll see for yourself), then outputting a tuple of the grid, and whether or not it had changed in the transition. As a result, my method code for Parts 1 and 2 ended up being identical, save for replacing some of the inputs to that state function.

Despite my roommate's protestations, I'm quite proud of my neighbour-counting functions. Sure, one of them uses a next(filter()) shorthand[2] – and both make heavy (ab)use of Python's new walrus operator, but they do a pretty good job making it obvious exactly what conditions they're looking for, while also taking full advantage of logical short-circuiting for conciseness.

Part 2 spoilers My Part 2 neighbour counter was largely inspired by my summertime fascination with constraint-satisfaction problems such as the [N-Queens problem](https://stackoverflow.com/questions/29795516/solving-n-queens-using-python-constraint-resolver). Since I realized that "looking for a seat" in the 8 semi-orthogonal directions was effectively equivalent to a queen's move, I knew that what I was really looking for was a delta value – how far in some [Manhattan-distance](https://www.wikiwand.com/en/Taxicab_geometry) direction I had to travel to find a non-aisle cell. If such a number didn't exist, I knew not to bother looking in that direction.

My simulations, whether due to poor algorithmic design or just on account of it being Python, ran a tad slowly. On the full input, Part 1 runs in about 4 seconds, and Part 2 takes a whopping 17 seconds to run fully. I'll be sure to check the subreddit in the coming hours for the beautiful, linear-algebraic or something-or-other solution that runs in constant time. A programmer I have been for many years; a computer scientist I have yet to become.

Day 12: Not terribly much to say on this one. Only that, if you're going to solve problems, it may be beneficial to read the instructions, lest

spoilers You cause your ship to turn clockwise by 90º... 90 times.

The second part was a fresh take on a relatively tired instruction-sequence problem. The worst part was the feeling of dread I felt while solving, knowing that my roommate – who consistently solves the problems at midnight, whereas I solve them in the morning – was going to awaken another Eldritch beast of Numpy and linear algebra for at least Part 2. Eugh.

Day 13: This was not my problem. I'm going to wrap my entire discussion of the day in spoilers, since I heavily recommend you try to at least stare at this problem for a while before looking at solutions.

spoilers The first part was... fine. The only real trick was figuring out how to represent the concept of "the bus arrives at a certain time" (i.e., modulo), and just compare that to some offset relative to your input departure time. Simulation works perfectly fine as a lazy solution, since your smallest input value is likely to be something like 13 (and thus your simulation time is bounded). The second part? Not so much. I knew that I was cutting corners on the first solution, since this problem was just *screaming* to look more mathy than code-y. And, turns out I was right: the problem could be solved on pen-and-paper if you were so inclined. If you look around on the subreddit and other comparable programmer spaces, you'll see everyone and their mother crying for the [Chinese Remainder Theorem](https://www.dave4math.com/mathematics/chinese-remainder-theorem/) and, since I have to establish boundaries around my time and energy lest I nerd-snipe myself into academic probation, I had to "give up" relatively quickly and learn how to use the algorithm. My roommate was able to come up with a solution on his lonesome, which actually relies on a fact I was also able to come up with before giving in. If you use a simple for-loop search to find numbers which satisfy any **two** of the modulo requirements, you'll quickly realize that the gap between any two succesive numbers is always equal to the product of those two numbers. (Well, technically, their LCM, but the bus routes are prime for a reason.) So, you can pretty quickly conclude that by the end of it, you'll be searching over the naturals with a step of ∏(buses), and the only trick left is to figure out what starting point you need. I think my roommate was at a bit of an advantage, though, owing to his confidence. He's definitely a lot better at math that I am, so he could dive into hunches headlong with a confidence that I lack. I found myself unable to follow hunches due to worry that I was either a) completely missing the point, or b) would accidentally make some critical arithmetic mistake early on that throws off all of my findings. In hindsight, I absolutely *should* have figured out that final Giant Step (hue), and then worked it backwards from the given answer to see what starting points made reasonable sense. But, again, I balked a bit at the sheer enormity of how much I didn't know about this kind of algebra, so I ended up needing a little more Google than brainpower. I'm chalking this problem up as a learning experience, as I truly had never heard of the CRT. I'm sure "linear systems of residue classes" will pop up again in a similar problem, and it's certainly a hell of a lot faster to compute than using sieves or similar algorithms. Also, I learned that Python 3.8 programmers had a distinct advantage over lesser-versioned Pythonistas, owing to the new functionality that was recently added to the `pow` builtin. In short, `pow` can now solve modular inverses, which is a massive timesave over implementing it yourself. I didn't know about this builtin at all, so I've continued to accomplish my goal of better understanding the standard library.

Day 14: The last day of this week! I really enjoyed today's challenge: it was tough, yet accessible from multiple approaches if you weren't a well-learned expert on bitwise masking.

Part 1 was just getting you acquainted with the world of bitmasking and the general workflow of the problem: number in, pass through mask, number out, store in memory. As usual, the formatted text made my Regex Lobe go off, and for once I gave in: it actually made extracting those integers a little easier, as I realized the addresses were of very variable length.

Part 2 was a perfect level of challenge for a Monday morning, methinks. It served me a proper punishment for not reading the updated challenge text appropriately, and I had to think about some clever modifications to my code from Part 1 to make Part 2 work effectively. My final solution wasn't all too efficient, but both parts run in a little under two seconds.

Part 2 spoilers I'm quite proud of my usage of `'0'` to denote a "soft" zero (i.e., the mask does nothing to this bit) and `'Z'` to denote a "hard" zero (i.e., the mask sets this bit to zero). I suppose I could have also inverted the entire mask – setting all `0`s to `X`s and all `X`s to `0`s – to make the old parse function work normally, but this worked just as well and didn't require completely rejigging the masks to make them work a particular way.

[1]: I keep having to stop myself from using the acronym with which I'm familiar, lest I get in trouble with Tumblr's new puritan filters. I wonder if the similar acronym for dynamic programming would be of issue.

[2] If you're unfamiliar, this is a common competitive-programming idiom in Python for "the first element that satisfies..." JavaScript, unfortunately, takes the cake here, as it has a native Array#find method that works much better.

0 notes

aikungfu · 4 years ago

Link

The case fatality rate quantifies how dangerous COVID-19 is, and how risk of death varies with strata like geography, age, and race. Current estimates of the COVID-19 case fatality rate (CFR) are biased for dozens of reasons, from under-testing of asymptomatic cases to government misreporting. We provide a careful and comprehensive overview of these biases and show how statistical thinking and modeling can combat such problems. Most importantly, data quality is key to unbiased CFR estimation. We show that a relatively small dataset collected via careful contact tracing would enable simple and potentially more accurate CFR estimation.

What is the case fatality rate, and why do we need to estimate it?

The case fatality rate (CFR) is the proportion of fatal COVID-19 cases. The term is ambiguous, since its value depends on the definition of a ‘case.’ No perfect definition of the case fatality rate exists, but in this article, I define it loosely as the proportion of deaths among all COVID-19-infected individuals.

The CFR is a measure of disease severity. Furthermore, the relative CFR (the ratio of CFRs between two subpopulations) enables data-driven resource-allocation by quantifying relative risk. In other words, the CFR tells us how drastic our response needs to be; the relative CFR helps us allocate scarce resources to populations that have a higher risk of death.

Although the CFR is defined as the number of fatal infections, we can not expect that dividing the number of deaths by the number of cases will give us a good estimate of the CFR. The problem is that both the numerator (#deaths) and the denominator (#infections) of this fraction are uncertain for systematic reasons due to the way data is collected. For this reason, we call that estimator “the naive estimator”, or simply deaths/cases, and denote it as $E_{\rm naive}$.

Why are (all) CFR estimates biased?

Fig. 1 Dozens of biases can corrupt the estimation of the CFR. Surveillance data gives partial information within the ‘sampling frame’ (light blue rectangle). Edges on the graph correspond roughly to conditional probabilities; e.g., the edge from D to DF is the probability a person dies if they are diagnosed with COVID-19.

In short, all CFR estimates are biased because the publicly available data is biased. We have reasson to believe that we are losing at least 99.8% of our sample efficiency due to this bias. There is a “butterfly effect” caused by non-random sampling: a tiny correlation between the sampling method and the quantity of interest can have huge, destructive effects on an estimator. Even assuming a tiny 0.005 correlation between the population we test and the population infected, testing 10,000 people for SARS-CoV-2 is equivalent to testing 20 individuals randomly. For estimating the fatality rate, the situation is even worse, since we have ample evidence that severe cases are preferentially diagnosed and reported. In the words of Xiao-Li Meng, “compensating for [data] quality with quantity is a doomed game.” In our HDSR article, we show that in order for the naive estimator $E_{\rm naive}$ to converge to the correct CFR, there must be no correlation between fatality and being tested — but severe cases are much more likely to be tested. Government and health organizations have been explicitly reserving tests for severe cases due to shortages, and severe cases are likely to go to the hospital and get tested, while asymptomatic ones are not.

The primary source of COVID-19 data is population surveillance: county-level aggregate statistics reported by medical providers who diagnose patients on-site. Usually, somebody feels sick and goes to a hospital, where they get tested and diagnosed. The hospital reports the number of cases, deaths, and sometimes recoveries to local authorities, who release the data on a weekly basis. In reality, there are many differences in data collection between nations, local governments, and even hospitals.

Dozens of biases are induced by this method of surveillance, falling coarsely into five categories: under-ascertainment of mild cases, time lags, interventions, group characteristics (e.g. age, sex, race), and imperfect reporting and attribution. An extensive (but not exhaustive) discussion of the magnitude and direction of these biases is in Section 2 of our article. Without mincing words, current data is extremely low quality. The vast majority of people who get COVID-19 go undiagnosed, there are misattributions of symptoms and deaths, data reported by governments is often (and perhaps purposefully) incorrect, cases are defined inconsistently across countries, and there are many time-lags. (For example, cases are counted as ‘diagnosed’ before they are ‘fatal’, leading to a downward bias in the CFR if the number of cases is growing over time.) Figure 1 has a graphical model describing these many relationships; look to the paper for a detailed explanation of what biases occur across each edge.

Correcting for biases is sometimes possible using outside data sources, but can result in a worse estimator overall due to partial bias cancellation. This is easier to see through example than it is to explain. Assume the true CFR is some value $p$ in the range 0 to 1 (i.e., deaths/infections is equal to $p$). Then, assume that because of under-ascertainment of mild cases, there are too many fatal cases being reported, which means $E_{\rm naive}$ converges to $bp > p$ (in other words, it is higher than it should be by a factor of $b$). Also assume the time-lag between diagnosis and death causes the proportion of deaths to diagnoses to decrease by the same factor $b$. Then, $E_{\rm naive}$ converges to $b(p/b)=p$, the correct value. So, even though it might seem to be an objectively good idea to correct for time-lag between diagnosis and death, it would actually result in a worse estimator in this case, since time-lag is helping us out by cancelling out under-ascertainment.

The mathematical form of the naive estimator $E_{\rm naive}$ allows us to see easily what we need to do to make it unbiased. With $p$ being the true CFR, $q$ being the reporting rate, and $r$ being the covariance between death and diagnosis, the mean of $E_{\rm naive}$ is:

This equation is pretty easy to understand. We wanted $\mu$ to be equal to $p$. Instead, we got an expression that depends on $r$, $q$, and $N$. The $r/q$ term is the price we pay if people who are diagnosed are more likely to eventually die. We want $r/q=0$, but in practice, $r/q$ is probably much larger than $p$. (Actually, if we assume the CFR is around 0.5% and the measured CFR is 5.2% on June 22, 2020, then $r/q \ge 0.047 \gg 0.005$.) In other words, $r/q$ is the bias, and it can be large. The term $p$ is the true CFR, which we want. And the factor $(1−(1−q)^N)$ is what we pay because of non-response; however, it’s not a big deal, because it disappears quite fast as the number of samples $N$ grows. So really, our primary concern should be achieving $r=0$, because — and I cannot stress this enough — $r/q$ does not decrease with more samples; it only decreases with higher quality samples.

What are strategies for fixing the bias?

In our article, we outline a testing procedure that helps fix some of the above dataset biases. If we collect data properly, even the naive estimator $E_{\rm naive}$ has good performance.

In particular, data should be collected via a procedure like the following:

Diagnose person $P$ with COVID-19 by any means, like at a hospital.

Reach out to contacts of $P$. If a contact has no symptoms, ask them to commit to getting a COVID-19 test.

Test committed contacts after the virus has incubated.

Keep data with maximum granularity while respecting ethics/law.

Follow up after a few weeks to ascertain the severity of symptoms.

For committed contacts who didn’t get tested, call and note if they are asymptomatic.

This protocol is meant to decrease the covariance between fatality and diagnosis. If patients commit to testing before they develop symptoms, this covariance simply cannot exist. However, there may still be issues with people dropping out of the study; if this is a problem in practice, it can be mitigated by a combination of incentives (payments) and consistent follow-ups.

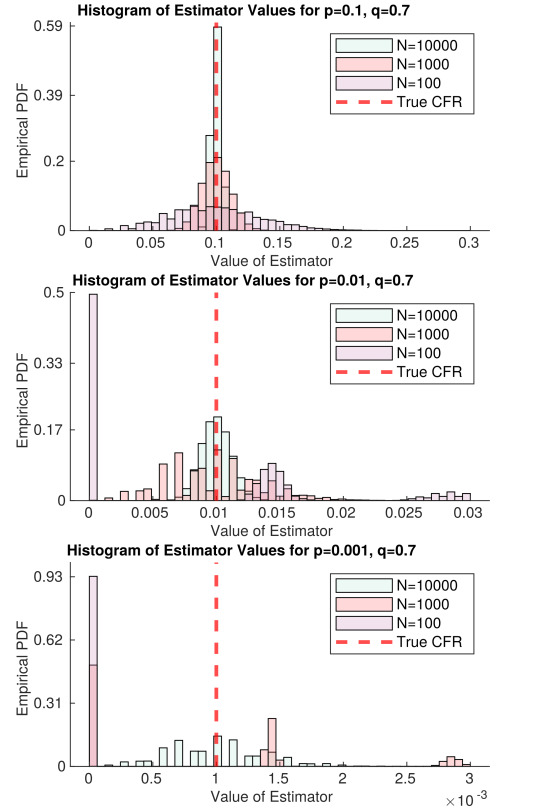
Fig. 2 Assuming data collection induces no correlation between disease severity and diagnosis, as the true CFR decreases, it requires more samples to estimate. The variable p is the true CFR, and q is the response rate. Each histogram represents the probability the naive estimator will take on a certain value, given N samples of data (different colors correspond to different values of N). The three stacked plots correspond to different values of p; the smaller p is, the harder it is to estimate, since death becomes an extremely rare event.

Figure 2 represents an idealized version of this study. In the best case scenario, there is no covariance between death and diagnosis. Then, we only need $N=66$ samples for our estimator of the CFR to be approximately unbiased, even if $p=0.001$ ($1/1000$ cases die). Problems remain in the case that $p$ is small; namely, death is so rare that we need tons of samples to decrease the variance of our estimator. This will require lots of samples. But even if no deaths are observed, we get a lot of information about $p$; for example, if $N=1000$ and we have not observed a single death, then we can confidently say that $p<0.01$ within the population we are sampling. This is simply because in the second panel of Figure 2, there is nearly zero mass in the $N=1000$ histogram at $E_{\rm naive} = 0$. With this in mind, we could find the largest possible p that is consistent with our data — this would be a conservative upper bound on $p$, but it would be much closer to the true value than we can get with current data.

This strategy mostly resolves what we believe is the largest set of biases in CFR estimation — under-ascertainment of mild cases and time-lags. However, there will still be lots of room for improvement, like understanding the dependency of CFR on age, sex, and race. (In other words, the CFR is a random quantity itself, depending on the population being sampled.) Distinctions between CFRs of these strata may be quite small, requiring a lot of high-quality data to analyze. If $p$ is extremely low, like 0.001, this may require collecting $N=100,000$ or $N=1,000,000$ samples per group. Perhaps there are ways to lower that number by pooling samples. Even though making correct inferences will require careful thought (as always), this data collection strategy will make it much simpler.

I’d like to re-emphasize a point here: collecting data as above will make the naive estimator $E_{\rm naive}$ unbiased for the sampled population. But the sampled population may not be the population we care about. However, there is a set of statistical techniques collectively called ‘post-stratification’ that can help deal with this problem effectively — see Mr. P.

If you read our academic article, we provide some thoughts on how to use time-series data and outside information to correct time-lags and relative reporting rates. Our work was very heavily based on one of Nick Reich’s papers. However, as I claimed earlier, even fancy estimators cannot overcome fundamental problems with data collection. I’ll defer discussion of that estimator, and the results we got from it, to the article. I’d love to hear your thoughts on it.

CFR estimation is clearly a difficult problem — but with proper data collection and estimation guided by data scientists, I still believe that we can get a useful CFR estimate. This will help guide public policy decisions about this urgent and ongoing pandemic.

This blog post is based on the following paper:

On Identifying and Mitigating Bias in the Estimation of the COVID-19 Case Fatality Rate. Anastasios Angelopoulos, Reese Pathak, Rohit Varma, Michael I. Jordan Harvard Data Science Review Special Issue 1 — COVID-19: Unprecedented Challenges and Chances. 2020.

from The Berkeley Artificial Intelligence Research Blog https://ift.tt/3i72v03 via A.I .Kung Fu

#Blogger

0 notes

wingedbreadfury · 6 years ago

Text

Test bank for Straightforward Statistics 1st Edition by Chieh Chen Bowen

This is completed downloadable of Test bank for Straightforward Statistics 1st Edition by Chieh Chen Bowen

Instant download Test bank for Straightforward Statistics 1st Edition by Chieh Chen Bowen

View sample:

http://testbankair.com/wp-content/uploads/2018/07/Test-bank-for-Straightforward-Statistics-1st-Edition-by-Chieh-Chen-Bowen.pdf

Product Descriptions

Straightforward Statistics by Chieh-Chen Bowen is written in plain language and connects material in a clear, logical manner to help students across the social and behavioral sciences develop a “big picture” understanding of foundational statistics. Each new chapter is purposefully connected with the previous chapter for a gradual accrual of knowledge from simple to more complex concepts―this effective, cumulative approach to statistics through logical transitions eases students into statistics and prepares them for success in more advanced quantitative coursework and their own research.

Test bank for Straightforward Statistics 1st Edition by Chieh Chen Bowen

Table of Content:

Chapter 1: Introduction to Statistics What Is Statistics? Population Versus Sample Descriptive Statistics and Inferential Statistics Sampling a Population Random Sampling Methods Simple Random Sampling Systematic Sampling Stratified Sampling Cluster Sampling Scales of Measurement Nominal Scale Ordinal Scale Interval Scale Ratio Scale Variable Classifications Discrete Versus Continuous Variables Independent Variables Versus Dependent Variables Required Mathematical Skills for This Course Statistical Notation Exercise Problems Solutions With EXCEL Step-by-Step Instructions When Needed Chapter Resources What You Learned Key Words Learning Assessment

Chapter 2: Summarizing and Organizing Data What You Know and What Is New Frequency Distribution Table Organizing and Summarizing Categorical Variables Organizing and Summarizing Numerical Variables Graphs Bar Graphs and Histograms Pie Charts Common Distribution Shapes Uniform Distribution Normal Distribution Skewed Distribution EXCEL Step-by-Step Instruction for Calculating &?#8721;X from Frequency Table and Constructing a Bar Graph Exercise Problems Solutions Chapter Resources What You Learned Key Words Learning Assessment

Chapter 3: Descriptive Statistics What You Know and What Is New Measures of Central Tendency Mode Median Mean Measures of Variability Range Variance and Standard Deviation for a Population Variance and Standard Deviation for a Sample Boxplot: 5-Number Summary Exercise Problems Solutions With EXCEL Step-by-Step Instructions Chapter Resources What You Learned Key Words Learning Assessment

Chapter 4: Standard Z Scores What You Know and What Is New Standard Z Scores Z Scores for a Population Z Scores for a Sample Empirical Rule for Variables With a Normal Distribution Exercise Problems Solutions Chapter Resources What You Learned Key Words Learning Assessment

Chapter 5: Basic Principles of Probability What You Know and What Is New Basic Terms and Mathematical Operations in Probability Basic Terms in Probability Mathematical Operations for Probabilities Binomial Probability Distribution Practical Probability Application: Winning the Mega-Million Lottery The Dice Game Linkage Between Probability and Z Score in Normal Distribution Probabilities, Z Scores, and Raw Scores Exercise Problems Solutions Chapter Resources What You Learned Key Words Learning Assessment

Chapter 6: The Central Limit Theorem What You Know and What Is New Sampling Error Sampling Distribution of the Sample Means and the Central Limit Theorem The Law of Large Numbers Relationships Between Sample Means and the Population Mean Exercise Problems Solutions Chapter Resources What You Learned Key Words Learning Assessment

Chapter 7: Hypothesis Testing What You Know and What Is New Type I Error and Type II Error The Four-Step Process to Conduct a Hypothesis Test Step 1: Explicitly State the Pair of Hypotheses Step 2: Identify the Rejection Zone for the Hypothesis Test Step 3: Calculate the Test Statistic Step 4: Make the Correct Conclusion Examples of the Four-Step Hypothesis Test in Action Directional Versus Non-Directional Hypothesis Testing Exercise Problems Solutions Chapter Resources What You Learned Key Words Learning Assessment

Chapter 8: One-Sample t Test When Sigma Is Unknown What You Know and What Is New The Unknown Sigma and Conducting the One-Sample t Test The t-Distribution, a Specific Curve for Every Degree of Freedom Confidence Intervals Point Estimate Interval Estimate Exercise Problems Solutions With EXCEL Step-by-Step Instructions Chapter Resources What You Learned Key Words Learning Assessment

Chapter 9: Independent Samples t Tests What You Know and What Is New Introducing Independent Samples and the Decision Rule on Equal Variances Decision Rule for Equal Variances Assumed Versus Equal Variances Not Assumed Equal Variances Assumed Equal Variances Not Assumed Using SPSS to Run Independent-Samples t Tests Confidence Intervals of the Mean Difference Effect Sizes Exercise Problems Solutions Chapter Resources What You Learned Key Words Learning Assessment

Chapter 10: Dependent-Sample t Test What You Know and What Is New Introducing Dependent-Sample t Tests Calculations and the Hypothesis-Testing Process in Dependent-Sample t Tests Mean, Standard Deviation, and Standard Error of the Differences Hypothesis Testing for Dependent-Sample t Tests Confidence Interval of the Differences Effect Size for the Dependent-Sample t Test Using SPSS to Run Dependent-Sample t Tests Exercise Problems Solutions Chapter Resources What You Learned Key Words Learning Assessment

Chapter 11: Correlation What You Know and What Is New Pearson’s Correlation Pearson’s Correlation Formulas Describing and Interpreting Pearson’s r Showing the Pearson’s Correlation in Action Hypothesis Testing for the Pearson’s Correlation Interpretations and Assumptions of Pearson’s Correlation Interpretations of Pearson’s Correlation Assumptions of Pearson’s Correlation Special Types of Correlation Spearman’s Rank Correlation Partial Correlation Formula Point Biserial Correlation EXCEL Step-by-Step Instruction for Constructing a Scatterplot EXCEL Step-by-Step Instruction on Calculating Pearson’s r Exercise Problems Solutions Chapter Resources What You Learned Key Words Learning Assessment

Chapter 12: Simple Regression What You Know and What Is New Y-Intercept and Slope Hypothesis Testing With Simple Regression Standard Error of the Estimate The Mathematical Relationship Between Pearson’s r and the Regression Slope, b Assumptions for Simple Regression Step-by-Step Instructions on SPSS Exercise Problems Solutions Chapter Resources What You Learned Key Words Learning Assessment

Chapter 13: One-Way Analysis of Variance What You Know and What Is New Introducing ANOVA Between-Group Variance and Within-Group Variance Sum of Squares Between Sum of Squares Within Degrees of Freedom for Between Groups (df B) and Within Groups (df W) Hypothesis Testing With ANOVA Post Hoc Comparisons Statistical Assumptions of an ANOVA Effect Size for One-Way ANOVA Step-by-Step Instructions for Using SPSS to Run an ANOVA Exercise Problems Solutions Chapter Resources What You Learned Key Words Learning Assessment

Chapter 14: Chi-Square Tests for Goodness-of-Fit and Independence What You Know and What Is New The Chi-Square Expected Frequency Expected Frequency Under a One-Way Frequency Table Expected Frequency Under a Two-Way Contingency Table Goodness-of-Fit Tests Hypothesis Testing With the Chi-Square Goodness-of-Fit Test Chi-Square for Independence Hypothesis Testing With the Chi-Square Test for Independence Exercise Problems Solutions Chapter Resources What You Learned Key Words Learning Assessment Appendix A. The Standard Normal Distribution Table (Z Table) Appendix B. The t-Distribution Table (t Table) Appendix C. The F Table Appendix D. The Critical Values of Pearson’s Correlation Table (r Table) Appendix E. The Cirtical Values for Spearman’s Rank Correlation Table (r S Table) Appendix F. The Critical Values for the Point Biserial Correlation Table (rpbi Table) Appendix G. The Critical Values of the Studentized Range Distribution Table (q Table) Appendix H. The Critical Values for the Chi-Square Tests (Chi2 Table)

Product Details:

Language: English

ISBN-10: 1483358917

ISBN-13: 978-1483358918

ISBN-13: 9781483358918

See more :

Test bank for Statistics Plain and Simple 3rd Edition by Sherri L Jackson

You will be guided to the product download page immediately once you complete the payment. If you have any questions, or would like a receive a sample chapter before your purchase, please contact us via email : [email protected]

Need other solution manual / test bank ?

Go to testbankair.com and type solution manual or test bank name you want in search box. If it not available in website, you can send email to

[email protected] for request solution manual or test bank. We’ll reply you maximum 24 hours.

Also, you can read How to Instant download files after payment .

People Also Search:

Test bank for Straightforward Statistics 1st Edition by Chieh Chen Bowen

Straightforward Statistics 1st Edition by Chieh Chen Bowen instant dowload

Straightforward Statistics 1st Edition by Chieh Chen Bowen pdf

Straightforward Statistics 1st Edition by Chieh Chen Bowen study adi

#Straightforward #Statistics 1st #Chieh Chen Bowen #1483358917 #9781483358918

0 notes

knoldus · 7 years ago

Link

Hello everyone! In my previous blog, I explained the difference between RDD, DF, and DS you can find this blog Here

In this blog, I will try to explain How spark internally works and what are the Components of Execution: Jobs, Tasks, and Stages.

As we all know spark gives us two operations for performing any problem.

Transformation

Action

When we do the transformation on any RDD, it gives us a new RDD. But it does not start the execution of those transformations. The execution is performed only when an action is performed on the new RDD and gives us a final result.

So once you perform any action on RDD then spark context gives your program to the driver.

The driver creates the DAG(Directed Acyclic Graph) or Execution plan(Job) for your program. Once the DAG is created, driver divides this DAG to a number of Stages. These stages are the divided into smaller tasks and all the tasks are given to the executors for execution.

The Spark driver is responsible for converting a user program into units of physical execution called tasks. At a high level, all Spark programs follow the same structure: They create RDDs from some input, derive new RDDs from those using transformations, and perform actions to collect or save data. A Spark program implicitly creates a logical Directed Acyclic Graph (DAG) of operations. When the driver runs, it converts this logical graph into a physical execution plan.

So let’s take an example of word count for better understanding:-

val rdd = sc.textFile("address of your file") rdd.flatMap(_.split(" ")).map(x=>(x,1)).reduceByKey(_ + _).collect

Here you can see collect is an action which will collect all data and give final result. As explained above, when I perform collect action the spark driver creates a DAG.

In the image above, you can see one job is created and executed successfully.

Now let’s have a look at DAG and it’s stages.

Here you can see spark created the DAG for the program written above and divided the DAG into two stages. In this DAG you can see a clear picture of the program, first the text file is read, then the transformations like map, flatMap are applied and finally the reduceBykey is executed.

But why spark divided this program into two stages, why not more than two or less than two? Basically it depends on shuffling, like whenever you perform any transformation where the spark needs to shuffle the data by communicating to the other partitions it creates other stages for such transformations. And the transformation which does not require the shuffling of your data, it creates a single stage for it.

Now let’s have a look at tasks that how many tasks have been created by the spark –

As I mentioned earlier that spark driver divides DAG stages into tasks. Here you can see for each stage is divided into two tasks. But why spark divided only two tasks for each stage? So it depends on your number of partitions. In this program, we have only two partitions so each stage is divided into two tasks. And single task runs on a single partition.

The number of tasks for a Job is = ( no of your stages * no of your partitions )

Now I think you people may have a clear picture that how spark works internally.

#WordPress

0 notes

whitechnoleg · 8 years ago

Photo

Graphs Interview Questions // techiedelight.com/graphs-interview-questions // A graph is an ordered pair G = (V, E) comprising a set V of vertices or nodes and a collection of pairs of vertices from V called edges of the graph. Graph For example for above graph, V = { 1, 2, 3, 4, 5, 6 } E = { (1, 4), (1, 6), (2, 6), (4, 5), (5, 6) } Below is the list of commonly asked graphs interview questions – Graph Implementation using STL Graph Implementation in C++ without using STL Breadth First Search (BFS) | Iterative & Recursive Implementation Depth First Search (DFS) | Iterative & Recursive Implementation Arrival and Departure Time of Vertices in DFS Types of edges involved in DFS and relation between them Bipartite Graph Minimum number of throws required to win Snake and Ladder game Topological Sorting in a DAG Transitive Closure of a Graph Check if an undirected graph contains cycle or not Total paths in given digraph from given source to destination having exactly m edges Determine if an undirected graph is a Tree (Acyclic Connected Graph) 2-Edge Connectivity in the graph 2-Vertex Connectivity in the graph Check if given digraph is a DAG (Directed Acyclic Graph) or not Disjoint-Set Data Structure (Union-Find Algorithm) Chess Knight Problem – Find Shortest path from source to destination Check if given Graph is Strongly Connected or not Check if given Graph is Strongly Connected or not using one DFS Traversal Union-Find Algorithm for Cycle Detection in undirected graph Kruskal’s Algorithm for finding Minimum Spanning Tree Single-Source Shortest Paths – Dijkstra’s Algorithm Single-Source Shortest Paths – Bellman Ford Algorithm All-Pairs Shortest Paths – Floyd Warshall Algorithm Print all k-colorable configurations of the graph (Vertex coloring of graph) Print All Hamiltonian Path present in a graph Greedy coloring of graph #graphs-interview-questions

#graphs

0 notes

eatsleepmath · 8 years ago

Text

Hilbert spaces, 1:

I’ve been reading Pedersen’s Analysis Now for a model-theoretic functional analysis reading course this term. We’re starting the section on Hilbert spaces (and the theory of operators on Hilbert spaces) and it’s my turn to present, so I’ve written some notes that I’ll also post here.

Definition. A sesquilinear form on a vector space $X$ is a map \[( \cdot | \cdot) : X \times X \to \mathbb{F}\] which is linear in the first variable and conjugate linear in the second. To be precise, it’s additive in either variable, but compatible/$\mathbb{F}$-equivariant up to conjugation in the second variable.

Definition. To each sesquilinear form $(\cdot | \cdot)$ we define the adjoint form $( \cdot | \cdot )^*$ by \[(x | y)^* \overset{\operatorname{df}}{=} \overline{(y | x)},\] for all $x$ and $y$ in $X$. We say that the form is self-adjoint if it is its own adjoint. (When $\mathbb{F} = \mathbb{R},$ the term symmetric is used.)

Claim. When $\mathbb{F}$ is $\mathbb{C},$ a calculation (or simply observing that $S^1$ acts via isometries) shows that \[4(x | y) = \sum_{k = 0}^3 i^k(x + i^k y | x + i^k y).\]

Proof. Expanding the sum gives \[(x | x) + (y | x) + (x | y) + (y | y)\]\[+ i(x | x) + i(x|iy) + i(iy|x) + i(iy|iy)\]\[- (x|x) - (x|-y) - (-y|x) - (-y | -y)\]\[ -i (x | x) - i(x | -iy) - i(-iy | x) - i(-iy|-iy)\] \[= (x|x)(1 + i - 1 - i) + (y | x)(1 - 1 + 1 - 1)\]\[ + (x|y)(1 + 1 + 1 + 1) + (y|y)(1 -i^3 - 1 + i^3)\]\[= 4(x|y).\] $\square$

We say a sesquilinear form $( \cdot | \cdot)$ is positive if $(x|x) \geq 0$ for every $x \in X$; thus, for $\mathbb{F} = \mathbb{C}$ a positive form is automatically self-adjoint, since the above claim shows (after a nearly-identical calculation) that a sesquilinear form is self-adjoint if and only if $(x | x) \in \mathbb{R}$ for every $x \in X$.

On a real space, a positive form might not be symmetric. For example, take a nontrivial quadratic form.

Definition. An inner product on $X$ is a positive, self-adjoint sesquilinear form such that $(x | x) = 0$ implies $x = 0$ for all $x \in X$, i.e. the form is positive-definite in addition to being positive.

Definition. From similar computations from the claim above, we obtain the following polarization identities: in $\mathbb{C},$ \[4(x|y) = \sum_{k=0}^3 i^k || x + i^k y||^2,\] and in $\mathbb{R}$, \[4(x|y) = || x + y||^2 - ||x - y||^2.\]

Lemma. (Cauchy-Schwarz inequality) Let $\alpha$ be a scalar in $\mathbb{F}$. The formula \[|\alpha|^2 ||x||^2 + 2 \Re \alpha(x | y) + ||y||^2 = ||\alpha x + y||^2 \geq 0\] for $x$ and $y$ in $X$ immediately leads to the Cauchy-Schwarz inequality: \[|(x|y)| \leq ||x|| ||y||.\]

Inserting this into the above formula, it follows that the norm function $|| \cdot ||$ is subadditive, and therefore a seminorm on $X$. In the case when $( \cdot | \cdot)$ is an inner product, the homogeneous function $||x|| \overset{\operatorname{df}}{=} (x | x)^{½}$ is a norm, and equality holds in the Cauchy-Schwarz inequality if and only if $x$ and $y$ are scalar multiples of each other.

Lemma. Elementary computations show that the norm arising from an inner product space satisfies the parallelogram law, namely \[||x+y||^2 + ||x - y||^2 = 2(||x||^2 + ||y||^2).\]

Conversely, one way verify that if a norm satisfies the parallelogram law, then the polarization identities from before induce inner products on $X$ (which one depending, of course, on the ground field.)

Definition. A Hilbert space is a vector space $\mathfrak{H}$ with an inner product $( \cdot | \cdot )$, such that $\mathfrak{H}$ is a Banach space with respect to the associated norm.

Examples. - The Euclidean spaces are Hilbert spaces.

- The spaces of compactly-supported continuous functions on Euclidean spaces are a Hilbert space with inner product given by $(f | g ) \overset{\operatorname{df}}{=} \int f \overline{g} dx;$ the associated norm is the $2$-norm, and after completing we get the Hilbert space $L^2 \mathbb{R}$.

(More generally, you could replace the Lebesgue integral above with a Radon integral on a locally compact Hausdorff space and the same construction gives you a Hilbert space $L^2 X.$)

Algebraic direct sums iare formed as in $\mathbf{Ban}$, with the new inner product being defined pointwise.

Lemma. If $\mathbf{C}$ is a closed nonempty convex subset of a Hilbert space $\mathfrak{H}$, there is for each $y$ in $\mathfrak{H}$ a unique $x$ in $\mathfrak{C}$ that minimizes the distance from $y$ to $\mathfrak{C}$.

Proof. By translation variance, we can assume $y = 0$. Let $\alpha$ be the infimum of the norms of elements in $\mathfrak{C}$. Choose a sequence $(x_n)$ from $\mathfrak{C}$ witnessing this.

For any $y$ and $z$ in $\mathfrak{C}$, the parallelogram law (and convexity, whence $½(y+z) \in \mathfrak{C}$) gives \[2 \left( ||y||^2 + ||z||^2\right) = ||y+z||^2 \geq 4 \alpha^2 + ||y - z||^2,\] Hence, when $y = x_n$ and $z = x_m$, $(x_n)$ is a Cauchy sequence, so by completeness of a Hilbertspace there is a limit $x$ with $||x|| = \alpha$.

Furthermore, since the topology is Hausdorff, the limit is unique. $\square$

Theorem. For a closed subspace $X$ of a Hilbert space $\mathfrak{H}$, let $X^{\perp}$ be the subspace of all elements orthogonal to all of $X$. Then each vector $y \in \mathfrak{H}$ has a unique decomposition $y = x + x^{\perp}$, and $x$ and $x^{\perp}$ are the nearest points in $X$ and $X^{\perp}$ to $y$; furthermore $\mathfrak{H} = X \oplus X^{\perp}$ and $\left(X^{\perp}\right)^{\perp} = X.$

Proof. More or less automatic verification.

Given $y$ in $\mathfrak{H}$ we take $x$ to be the nearest point in $X$ to $y$ gotten by the previous lemma; put $x^{\perp}$ to be $y - x$. For every $z \in X$ and $\epsilon > 0$,

\[||x^{\perp}||^2 = ||y - x||^2 \leq ||y - (x + \epsilon z)||^2\]

\[= ||x^{\perp} - \epsilon z||^2 = ||x^{\perp}||^2 - 2 \epsilon \Re(x^{\perp}|z) + \epsilon^2||z||^2.\]

It follows that $2 \Re(x^{\perp}|z) \leq \epsilon ||z||^2$ for every $\epsilon > 0$, whence $\Re(x^{\perp}|z) \leq 0$ for every $z$. Since $X$ is a linear subspace, this implies that $(x^{\perp}|z)$ is zero, so that $x^{\perp}$ deserves its name and is in $X^{\perp}$. $\square$

Corollary. For every subset $X \subset \mathfrak{H}$, the smallest closed subspace of $\mathfrak{H}$ containing $X$ is $X$-double perp. In particular, if $X$ is a subspace of $\mathfrak{H}$, then $\overline{X}$ is $X$-double perp.

Proposition. The maps $\Phi \overset{\operatorname{df}}{=} ( \cdot | x )$ are conjugate linear isometries of $\mathfrak{H}$ onto $\mathfrak{H}^*$.

Proof. Tautologically conjugate-linear; $\Phi$ is maximized by CZ-inequality on $x/||x||$ on the unit ball, so the norm of $\Phi$ is precisely $||x||$. $\square$

Remark. Take $\varphi$ in $\mathfrak{H}^* \backslash \{0\}$, and put $X = \ker \varphi$. Since $X$ is a proper closed subspace of $\mathfrak{H}$, there is a vector $x \in X^{\perp}$ such that $\varphi(x) = 1.$ For every $y \in \mathfrak{H}$, we see that $y - \varphi(y) x \in X$, hence \[(y | x) = (y - \varphi(y) x + \varphi(y) x | x) = \varphi(y) ||x||^2.\] It follows that $\varphi = \Phi(||x||^{-2} x).$

Definition. We define the weak topology on a Hilbert space $\mathfrak{H}$ as the initial topology corresponding to the family of functionals $x \mapsto (x | y),$ so essentially the weak topology it induces…on itself. Since it is isometric with its dual, the weak topology on $\mathfrak{H}$ is the weak-star topology on $\mathfrak{H}^*$ pulled back via the isometry, and the unit ball in $\mathfrak{H}$ is weakly compact.

We’ll see that every operator in $\mathbf{B}(\mathfrak{H})$ is continuous as a function $\mathfrak{H} \to \mathfrak{H}$ when both copies have the weak topology; we say that $T$ is weak-weak continuous.

Conversely, if $T$ is a weak-weak cts operator, we can invoke the closed graph theorem to see that $T \in \mathbf{B}(\mathfrak{H})$. Indeed, if $x_n \to x$ and $T x_n \to y$ in the norm topology, then $x_n \to x$ and $T x_n \to y$ weakly since the norm topology refines the weak topology; by assumption $T x_n \to Tx$ weakly, whence $Tx = y,$ as was required.

Similarly, every norm-weak continuous operator on $\mathfrak{H}$ is bounded. We’ll see later operator that is weak-norm continuous must have finite rank, which is neat; we’ll later also modify this to give a characterization of the compact operators (which are a good candidate for treating infinitesimal elements.)

#math #functional analysis #hilbert spaces

47 notes · View notes