#dedekind numbers
Explore tagged Tumblr posts
Text
The task I wanted to do:
- task 1: Visualize the fourth dedekind number
What I needed to do in order to do task 1:
- task 1.1: Draw a hypercube and
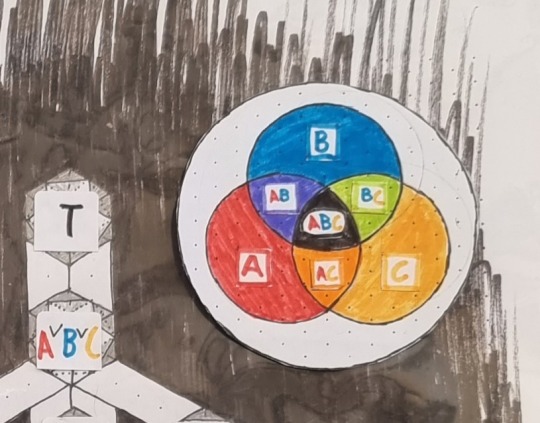
- task 1.2: then give each of the 16 vertices a name - which is the 16 different "cells" (I dunno which word to use, sorry) of a venn diagram with 4 overlapping sets plus a circle around that 4-venn diagram.
- - -- ---
//additional info: For the 3rd dedekind number visualization I already posted I needed to use 20 cubes. Each of the 8 vertices of a cube was related to 3 sets - A, B and C - and the intersections of these sets. (AB, AC, BC, ABC)
You remember this post:

... and these details:

...and now back to the 4th dedekind number, which follows the same principle, - but in 4 dimensions.
- So we need a hypercube - and a 4th set/letter:
Now we have 4 letters - alias 4 sets
- and 11 combinations of these sets:
AB, AC, AD, BC, BD, CD, (6)
ABC, ABD, ACD, BCD, (4)
ABCD (1)
=> 11 different intersections + 4 "pure" sets. (sorry for ignorant wording)
So, we have 15 of these now. What is with the 16th (as the hypercube has 16 vertices)? Yeah, that one is the circle you imagine around the 4-set venn diagram.
- - -- ---
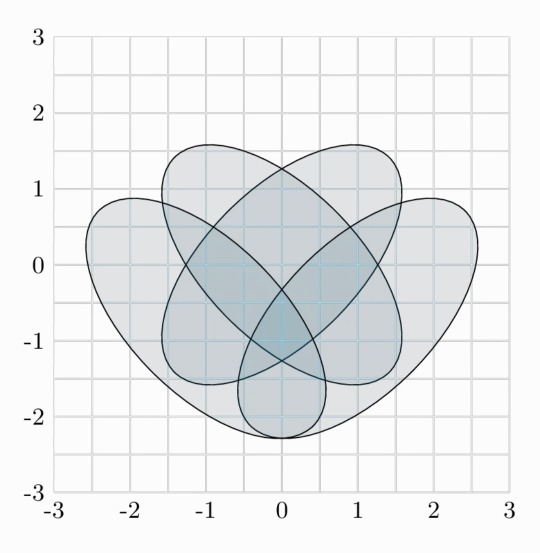
This is a 4-set venn diagramm btw:
--- -- - -
So, back to me attempting to do the 4th dedekind-number visualization:
So I started to draw that venn diagram using ellipses, but I slightly altered it, because I wanted to use my isometric grid paper. (The angles of my drawing are different than in the picture depicted above.)
I started to draw the 4 ellipses, and I somehow started to see two intertwined/interlocked tubes due to the additional helplines I used for drawing.
Then I started to use my thicker black pen to make this effect of these two interlocked tubes more visible:
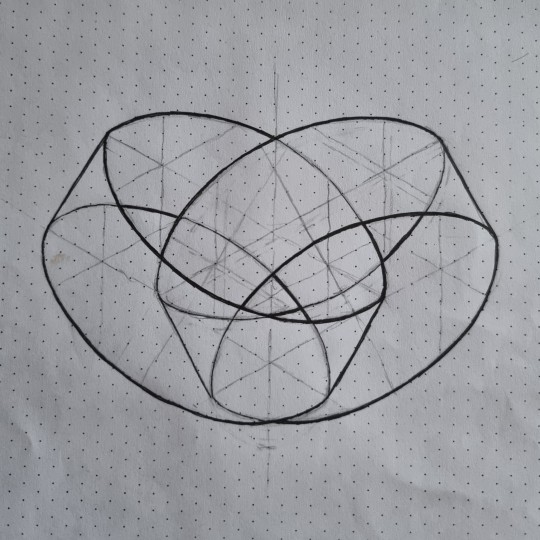
Now I plan to write the sets/letters at the backside of that piece of paper - in mirrored, so I can hold this piece of paper (with the tube drawing in front) against the light - and see the letters of the set names shining through.
i might also add some details to the tubes.
#my train of thought is the most dispersed scattered mess of whatever one might call this fuckery#... and yet in the end this clusterfuck of incoherent thought ramblings still make sense#the nonsense facility works nonsensically at producing non-nonsensical side-products#clusterfuck of nonsense thought ramblings#math#math or such idk#math art#dedekind numbers#venn diagram#venn diagrams#4th dedekind number#hypercube#set theory#sets#optical illusion#artsy#art#mathy art#my art#wip
67 notes
·
View notes
Text
I am very tired and constantly switch from project to another project with utterly different topics - but I am glad I could continue with this illustration I started some weeks ago.
I don't know much about the Dedekind numbers yet - nevertheless, the few information my attention span allowed me to save in my memory inspired me to start this lil illustration/visualization/whatever/...

Third Dedekind number illustration/visualization - WIP
#math visualization#dedekind numbers#dedekind number#third dedekind number#mathy art#math art#mathy#my art#artsy
89 notes
·
View notes
Text
Making history with 42 digits, scientists at Paderborn University and KU Leuven have unlocked a decades-old mystery of mathematics with the so-called ninth Dedekind number. Experts worldwide have been searching for the value since 1991. The Paderborn scientists arrived at the exact sequence of numbers with the help of the Noctua supercomputer located there. The results will be presented in September at the International Workshop on Boolean Functions and their Applications (BFA) in Norway. What started as a master's thesis project by Lennart Van Hirtum, then a computer science student at KU Leuven and now a research associate at the University of Paderborn, has become a huge success. The scientists join an illustrious group with their work. Earlier numbers in the series were found by mathematician Richard Dedekind himself when he defined the problem in 1897, and later by greats of early computer science such as Randolph Church and Morgan Ward. "For 32 years, the calculation of D(9) was an open challenge, and it was questionable whether it would ever be possible to calculate this number at all," Van Hirtum says.
Continue Reading
101 notes
·
View notes
Text
They did it, boys. It took 32 years and supercomputers, but they finally pulled it off.
They have calculated D(9), the ninth Dedekind Number.
Here it is. Are you ready for this?
286 386 577 668 298 411 128 469 151 667 598 498 812 366
How did they do it, you ask? Well, here is a handy chart:

...I have absolutely no idea what any of this means.
But it looks like those things in Kabbalah and Gnosticism that you use to control demons.

I'm not saying mathematicians are all mathemagicians. But I am saying that if they were all in fact evil wizards, I would not be able to tell.
15 notes
·
View notes
Text
Dedekind cuts can fuck right off (: It’s all about my beloved, Cauchy sequences<3
#I’m reviewing real analysis to prep for measure theory#and I forgot how much better than dedekind cuts Cauchy sequences are when constructing the real numbers#another win for Terry Tao and another L for baby rudin#chris.txt
0 notes
Note
It's funny that we're talking about the partition ("Dedekind cut") definition of reals here because those actually do have an equivalent to the 0.999... vs 1 thing - the partition corresponding to 0.999... is where all the numbers smaller than 1 are in one set and all the numbers equal to or larger than 1 are in the other, and the partition corresponding to 1 is where all the numbers smaller than or equal to 1 are in one set and all the numbers larger than 1 are in the other. (If you're finding it hard to follow my description: the difference is that the exact number 1 is on the right side vs. on the left side.)
In practice there's a standard rule that only one partition in such a pair (those pairs exist for any rational) counts as a valid representation of the corresponding rational as a real number (I don't actually recall which one offhand) and the other is an invalid representation, but the very fact that we need such a rule is evidence that 0.999... is meaningfully distinct from 1 as a concept even if it, fundamentally, comes out to the same number.
But yes, 0.999... is, in fact, equal to 1, very much like how 2+2 is equal to 4 - the concept "2+2" is distinct from the concept "4" (and both are distinct from the concept "3+1", or "9-5", or "the number of sides in a square"), but they represent the same underlying number.
I have a math question: Why does it matter that .9999infinity9 isn't actually equal to 1? Like, I get that it MUST matter, but I don't quite understand where or how? Are there any practical applications where the difference would matter, or is it purely in the realm of the theoretical?
so first off, worth saying that .9 repeating is equal to 1 in base 10. not approximately equal, just equal. there are a lot of non-mathematically rigorous ways to intuit that (ie, try to think of a number between the two, since for any approximation there exists a number between the approximation and the actual number) and rigorous ways to prove that (which involve talking about what the real number line actually is and what a limit is).
but yeah, this is truly, purely theoretical. it’s almost semantic, to be honest - the proofs that it is true mostly involve walking the reader through the proper definitions, since after you understand them it’s pretty much trivial.
it serves mostly as a litmus test for your understanding of limits, as opposed to anything with a practical usage.
#0.999...#1#1+1=2#2+2=4#Dedekind cuts#math#logic#real numbers are a mess#formal logic is a mess too sometimes
311 notes
·
View notes
Note
what’s your favorite number
this is a really hard question. Its probably 2, since it makes for an amazing base and is just generally very useful, like, when you have a+a, which is common, that turns into 2a. It's also the successor to 1, making it the first number thats not just defined directly by axioms like 0 and 1 and rather a consequence.
2 is also aesthetically fun, the way it swoops at the top and then sits on a sturdy base, with both a round and a sharp corner. So, that's my answer,
2
But! If we go further we can find lots of other numbers I also love. 6 is a really nice number because its small but not "weird" in any immediate way. It's not an identity, it's not prime, it's not a square, etc. If you have a formula or something and you want to check it with a number 6 usually works without running into common edge cases.
Leaving the Naturals, -1 is an amazing integer. Really useful for anything that alternates, I love the roots of unity and it's the first nontrivial of those. All the roots of unity are pretty amazing tho, highly recommend.
Rising further we get to the Rationals, which are honestly kinda boring imo. Shoutout to ½ for being the reciprocal of 2 but that's it.
Now, shit is gonna get Real. The Reals are an amazing set, lots of useful properties, a really cool field (the Rationals are also a field but they suck so the Reals get to be the cool field). The Reals contain just about every number you normally interact with, including all-time highs such as pi or e. All algebraic and transcendental numbers are in here, including my favourite, sqrt(2). The square root of 2 is real cool. It's fun geometrically, being a factor of the length of the hypotenuse of a right triangle where the legs are the same length. It's cool algebraically as being the easiest to introduce number thats real but not rational, I have fond childhood memories of learning that the Reals are Dedekind complete (of course that word was only introduced in high school) with this beautiful number as the example. It's reciprocal is also really cool and useful. sqrt(2) even has its own Wikipedia article.
Leaving behind the Reals, the Complex Numbers are just fun as a category. No longer ordered, basically acting as if R² was a field, just really fun. I don't really have a favourite complex number but I am a sucker for units for i gets nominated as my favourite here. All complex numbers are really cool. Shoutout to |0> and |1> (ket-zero and ket-one) for being cool in quantum computing and being vectors in a space using the field of the complex numbers.
There is lots more sets but I am not familiar enough with numbers to even come close to doing them justice. I hope your questions is answered, have a nice day <3
#math#asks#rambling about my special interests#i love math#numbers arent actually my favourite part but they are just very fundamental#sorry to my number theory mutuals but category theory has my heart#<3
22 notes
·
View notes
Text
if u go to whole foods they sell organic (natural) whole numbers and if u get a whole bunch of those (like countably infinite many) u can do some gmo shit and come up with all sorts of funky numbers like minus one and two and a half and if ur feeling really freaky [i physically cannot write out a complete dedekind cut of an irrational number]
15 notes
·
View notes
Text
when a mathematician who studies the real numbers wears a slutty little outfit they call it serving Dedekind cunt
24 notes
·
View notes
Text
i understand: what i'm bringing up is that given the very very long list of mathematical structures for which this (assigning each element to a number) is possible, what is it ontologically that determines which are numbers and which aren't? why do we say any random cauchy sequence is not a number, but special equivalence classes of them are? and my point is essentially your last paragraph: we rely on cultural assumptions as to what it means to "quack like a number" when we make the separation between the two, as is done for this tournament
Number Tournament: SIX vs STAR

[link to all polls]
6 (six)
seed: 9 (47 nominations)
previous opponent: thirty-nine
class: highly composite number
definition: the number of sides of both a regular shape that tiles the 2D plane as well as a regular shape that tiles 3D space
{0|0} (star)
seed: 41 (12 nominations)
previous opponent: twenty-four
class: nimber
definition: a fuzzy value from combinatorial game theory. it's very imnportant to understanding the evaluation of different positions in impartial games, games where actions are not restricted to either player
#i would also argue that there's no single thing as a 'number'#not only because a real number is not the same mathematical object as an integer#but also (as always) because of benecerraf's identification problem#we say that real numbers constructed through dedekind cuts are the same as real numbers constructed through cauchy sequences#but they're only the same up to isomorphism#is there a philosophical distinction to be made between the two?#should we consider sets between which there is an isomorphism to be the same?#id say a number is like a worm#there are definitely things that you can look at and say thats a worm#but many of those things are completely unrelated other than through the fact that they're animals
581 notes
·
View notes
Text
Today I went to the Technische Sammlungen Dresden with my friend, and it was very interesting!



Torus (mug) and genus-2 torus (Pretzel) (has a pretzel 2 or 3 holes? 3 actually??? )


Möbius strip:


#technische sammlungen#math#mathematics#dedekind-number#torus#mug#topology#mobius strip#mathy#mathpost#mathy stuffy#math stuff
164 notes
·
View notes
Text

Dedekind cuts: the unkindest cut of all. It segregates the rational numbers quite unfairly into all the smaller rational numbers versus all the larger rational numbers. We really should be treating all the rational numbers the same.
#white flower#macro photography#flowers of tumblr#original photographers#photographers on tumblr#flowers on tumblr#inner life of flowers#macro flower#flowers
9 notes
·
View notes
Text
The quest for the ninth Dedekind number was a formidable challenge that spanned over 32 years. The calculations involved were so complex and involved such large numbers that it was uncertain whether D(9) would ever be discovered. But undeterred by the complexity and the enormity of the task, mathematicians continued their pursuit.
50 notes
·
View notes
Text
i should DEFINITELY not tell my precalc students how the natural numbers are constructed via the peano axioms and how to create the reals via dedekind cuts
i should not tell my calc 3 students about tangent bundles, i should not tell my calc 3 students about tangent bundles...
#and yet.....#dw i am not mentioning dedekind cuts#but i did allude to the peano axioms#just in the sense that you can get every natural number by repeatedly adding one
12 notes
·
View notes
Text
In a world where I could magically change the lexicon, I think that "analytic numbers" is a much better name than "real numbers", because more than any sense of "reality" (meaningless - almost every real number is undefinable!), the real numbers are defined by an analytic criterion (Dedekind completeness).
"Algebraic number" unfortunately already has a useful meaning (is the root of a polynomial with integer coefficients) but in another universe would be a good name for the complex numbers (defined as they are as the algebraic closure of the reals).
7 notes
·
View notes
Note
This isn’t raygun, but I would say you are wrong re: prob-comb-history. Like, there’s a reason they call it the “Bernoulli distribution” (not my preferred name).
Besides that, I disagree. For instance, you talk about group theory, as a late 19th century concept, but already (abelian) groups are noticed by eg Kummer/Dedekind type algebraic number theory, in the mid-19th century, following Gauss’s earlier work on composition laws.
Other examples to be included are (1) Riemann surface theory/covering spaces, the direct precursor to turn of the 20th century algebraic topology a la Poincare, and (2) calculus of variations, 18th century and still exceedingly active in various guises.
Frankly, the nascent developing conversation seems misguided to me. The question must be refined. Of course the subjects alluded to above can be described in “20th century” terminology, but part of developing that terminology was to organize previous efforts.
Yeah, but I think I addressed this in my post. To wit:
So, ok, there's a sense in which many of these ideas existed in a different guise before they were formalized in the modern way. But the streamlining of all these messy, complex-seeming results from disparate parts of math into a single coherent set of frameworks is itself a useful development, it makes math easier, and these frameworks are part of what make modern math what it is. Modern mathematicians use them to fruitfully to do their job. Everything makes reference to groups, to topological spaces, to vector spaces, and so on.
The proto-topology of the nineteenth century contains in a sort of Platonic way "the same ideas" as the topology-per-se of today, but in terms of the ability to grab a problem and fruitfully throw topology techniques at it, they are not the same. The framing, the streamlining, the packaging—these are parts of the tool. In fact, you could argue that it's these very things that make all of mathematics powerful in the first place. It's not really the case, I think, that you could usefully frame the Zariski topology in terms of nineteenth century ideas about spaces. Maybe you could. But what we have today is much more powerful for that.
6 notes
·
View notes