#Operaciones entre Polinomios

[alineacionesdercdmallorcacontrar]

¿Cómo simplificar la expresión matemática 1/x + 2?

🎰🎲✨ ¡Obtén 500 euros y 200 giros gratis para jugar juegos de casino con solo un clic! ✨🎲🎰

¿Cómo simplificar la expresión matemática 1/x + 2?

Simplificación de fracciones

La simplificación de fracciones es un concepto fundamental en matemáticas que consiste en reducir una fracción a su forma más simple. Para simplificar una fracción, se deben dividir tanto el numerador como el denominador por el máximo común divisor de ambos números.

Por ejemplo, si tenemos la fracción 8/12, podemos simplificarla dividiendo ambos números por 4, que es el máximo común divisor de 8 y 12. De esta manera, obtenemos la fracción simplificada 2/3. Esta fracción es equivalente a la fracción original 8/12, pero está expresada en su forma más simple.

Simplificar fracciones es importante porque nos permite trabajar con números más manejables y comprender mejor las relaciones entre ellos. Además, las fracciones simplificadas son más fáciles de sumar, restar, multiplicar o dividir, ya que los cálculos son más sencillos y menos propensos a errores.

Es importante recordar que no todas las fracciones se pueden simplificar. Por ejemplo, las fracciones irreducibles o fracciones en su forma más simple no pueden reducirse aún más. Es fundamental dominar el proceso de simplificación de fracciones para resolver problemas matemáticos con mayor facilidad y precisión. ¡Practica este concepto y mejora tus habilidades matemáticas!

Expresiones algebraicas

Las expresiones algebraicas son fundamentales en el estudio de las matemáticas, ya que nos permiten representar y resolver problemas de una manera más general y abstracta. Una expresión algebraica está formada por números, letras y signos matemáticos, que se combinan siguiendo ciertas reglas.

En una expresión algebraica, las letras representan números desconocidos o variables, lo que nos permite realizar operaciones matemáticas sin necesidad de conocer los valores concretos de esas variables. Por ejemplo, la expresión algebraica "3x + 7" significa que multiplicamos la variable x por 3 y luego sumamos 7 al resultado.

Las expresiones algebraicas se utilizan en una amplia variedad de contextos, desde la resolución de ecuaciones simples hasta la modelización de fenómenos complejos en física, química o economía. Al manipular expresiones algebraicas, podemos simplificar problemas, factorizar polinomios, resolver ecuaciones o despejar incógnitas en funciones matemáticas.

Es importante entender las reglas básicas de las expresiones algebraicas, como la jerarquía de operaciones, las propiedades de los números reales y las leyes de los exponentes. Con una sólida comprensión de la algebra, podemos mejorar nuestras habilidades de resolución de problemas y razonamiento matemático.

En resumen, las expresiones algebraicas son una herramienta poderosa y versátil en el mundo de las matemáticas, que nos permite abordar problemas de manera abstracta y generalizada, facilitando la resolución de una amplia gama de situaciones matemáticas y científicas.

Suma de fracciones

La suma de fracciones es una operación matemática básica que consiste en combinar dos o más fracciones para obtener un resultado único. Para poder sumar fracciones, es fundamental que tengan el mismo denominador. En caso de que las fracciones tengan denominadores diferentes, primero se deben encontrar fracciones equivalentes con el mismo denominador antes de proceder con la suma.

Para sumar fracciones con el mismo denominador, simplemente se suman los numeradores y se conserva el mismo denominador. Por ejemplo, si queremos sumar 1/4 + 1/4, el resultado sería 2/4, que simplificado sería igual a 1/2.

En el caso de sumar fracciones con distintos denominadores, primero se buscan fracciones equivalentes. Por ejemplo, si queremos sumar 1/3 + 1/6, para encontrar un denominador común multiplicamos cruzadamente los denominadores: 3 * 6 = 18. Entonces, las fracciones equivalentes serían 2/6 + 1/6 = 3/6, que simplificado sería igual a 1/2.

Es importante recordar que al sumar fracciones, el resultado final puede necesitar simplificarse para expresarlo de manera más sencilla. La suma de fracciones es una operación fundamental en las matemáticas y se aplica en diversos contextos, desde la vida cotidiana hasta la resolución de problemas más complejos en ámbitos académicos y profesionales.

Fracciones simples

Las fracciones simples son un tema fundamental en matemáticas que suele causar confusión en muchos estudiantes. Una fracción simple es aquella en la que el numerador es menor que el denominador y no se puede simplificar aún más. Por ejemplo, 1/2 es una fracción simple, ya que el numerador (1) es menor que el denominador (2) y no comparten ningún divisor común mayor que 1.

Para trabajar con fracciones simples, es importante recordar algunas reglas básicas. En primer lugar, para sumar o restar fracciones simples, es necesario que tengan el mismo denominador. Si no es así, es necesario hallar el denominador común para poder operar con ellas. Para multiplicar fracciones simples, simplemente se multiplican los numeradores entre sí y los denominadores entre sí. Para dividir fracciones, se multiplica la primera fracción por el recíproco de la segunda fracción.

Es común encontrar fracciones simples en situaciones cotidianas, como al repartir una pizza en partes iguales o al calcular porcentajes. Por lo tanto, dominar el concepto de fracciones simples es esencial para desenvolverse con soltura en diversas situaciones de la vida diaria y en estudios más avanzados de matemáticas.

En resumen, las fracciones simples son una herramienta matemática básica pero imprescindible, que nos ayuda a entender y operar con cantidades fraccionarias de manera eficiente y precisa. Dominar este concepto nos permitirá resolver problemas con mayor facilidad y precisión en diversos contextos.

Operaciones matemáticas

Las operaciones matemáticas son la base de la aritmética y juegan un papel fundamental en la resolución de problemas en la vida cotidiana, así como en campos más complejos como la física, la ingeniería y la economía. Estas operaciones incluyen la suma, la resta, la multiplicación y la división, y son fundamentales para el desarrollo de habilidades matemáticas sólidas.

La suma es una operación que consiste en combinar dos o más valores para obtener un resultado total. Por otro lado, la resta se encarga de determinar la diferencia entre dos cantidades. La multiplicación es una operación repetitiva de suma, donde una cantidad se suma varias veces, y la división es la operación inversa a la multiplicación, donde un valor se divide en partes iguales.

Es fundamental comprender la jerarquía de las operaciones matemáticas, es decir, la secuencia en la que se deben realizar las operaciones para obtener el resultado correcto. Esto se conoce como el uso de paréntesis, exponentes, multiplicación, división, suma y resta en ese orden.

Dominar estas operaciones matemáticas es esencial para resolver problemas de manera eficiente y precisa. Además, fomenta el pensamiento crítico, la lógica y la resolución de problemas, habilidades que son valiosas en todos los aspectos de la vida. Por lo tanto, es importante practicar y perfeccionar estas operaciones para fortalecer nuestra comprensión matemática y mejorar nuestro rendimiento académico y profesional.

[triplenlace]

Funciones y polinomios / 2. División entre polinomios y raíces de un polinomio

División de polinomios Las operaciones de suma, resta y multiplicación de polinomios son triviales: se llevan a cabo siguiendo las reglas algebraicas usuales. Restar los polinomios y (Sol.: ) Multiplicar los polinomios y (Sol.: La división se realiza por el método que explicamos a continuación con un Dividir el polinomio entre . Sol.: Se escriben el dividendo, , y el divisor, , como en una…

[totumat]

Expresiones Racionales

Definimos una expresión racional como el cociente entre dos polinomios. Formalmente, si P(x) y Q(x) son dos polinomios con Q(x) distinto de cero, entonces el siguiente cociente será una expresión racional: P(x)/Q(x)

Habiendo estudiado las operaciones entre polinomios, particularmente la división de polinomios, podemos ampliar las operaciones entre fracciones como una herramienta para simplificar las operaciones entre polinomios antes de efectuarlas. También pudiera interesarte Definimos una expresión racional como el cociente entre dos polinomios. Formalmente, si y son dos polinomios con , entonces el…

[mateideas]

Suma y Resta de Fracciones Algebraicas

El procedimiento es el mismo que para sumar o restar fracciones numéricas, es decir, necesitamos tener el mismo denominador para sumar y restar fracciones y cuando no lo tenemos, tenemos que reducir las fracciones a denominador común, con la diferencia de que con las fracciones algebraicas, en vez de números, trabajamos con polinomios.

Suma y Resta de fracciones algebraicas con Igual denominador

La suma de fracciones algebraicas con el mismo denominador es otra fracción algebraica con el mismo denominador y cuyo numerador es la suma de los numeradores.

Ejemplo:

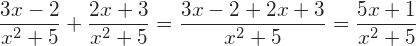
Suma y Resta de fracciones algebraicas con diferente denominador

Si las fracciones tienen distinto denominador en primer lugar se ponen las fracciones algebraicas a común denominador, posteriormente se suman los numeradores.

Pasos:

- Calculamos el común denominador que será el m.c.m. de los denominadores.

- Dividimos el común denominador entre los denominadores de las fracciones dadas y el resultado lo multiplicamos por el numerador correspondiente.

- Quitamos paréntesis

- Realizamos las operaciones en el numerador

- Sacamos factor común 2 en el numerador

- Simplificamos

Dato: La resta se soluciona de igual forma, salvo que el numerador en lugar de componerse de una suma se compone de una resta.

Te dejo de igual manera por acá un video en el cuál te puedas apoyar mejor, es algo largo pero te ayudará a comprender de mejor manera estos casos.

¡Nos vemos!

-Yaya

[ricardo-dat54]

Innovaciones tecnológicas

Teléfono

El telettrofono o teléfono fue inventado en el año 1854 por el inventor italiano Antonio Meucci. Lo construyó para conectar su oficina con su dormitorio y así poder hablar con su esposa, que estaba inmovilizada en cama por una enfermedad.

El dispositivo podía transmitir señales acústicas a distancia por medio de señales eléctricas. Era el precursor del teléfono actual, pero Meucci no tenía dinero para patentar el invento, de forma que su descubrimiento nunca fue reconocido.

Durante mucho tiempo, Alexander Graham Bell fue considerado el inventor del teléfono, pero solo porque fue el primero en patentar el dispositivo en 1876.

La primera llamada

La primera llamada sin cables tuvo lugar en 1973 gracias a Martin Cooper, ingeniero de la empresa de telecomunicaciones Motorola.

Durante los años siguientes, los avances tecnológicos permitieron desarrollar los primeros modelos de teléfono móvil, que permitían comunicarse desde cualquier lugar. En ese momento, la llamada podía tener una duración máxima de 30 minutos.

A partir de ahí, en la década de 1990 ya había infinidad de marcas que comercializaban teléfonos móviles. Algunos eran más compactos e incluso tenían una tapa para protegerlos de los golpes.

La siguiente gran incorporación de los dispositivos móviles fue la pantalla a color. Pero no fue hasta este siglo que apareció el primer teléfono con cámara incorporada que permitía hacer fotografías.

Después llegaron los mensajes de texto y los mensajes multimedia (que podía incluir imágenes y sonido). En 2007 se registraron hasta 1,9 trillones de mensajes en todo el mundo.

Teléfonos y relojes inteligentes

Steve Jobs revolucionó la industria del teléfono móvil y las nuevas tecnologías en 2007, cuando se presentó el primer modelo de iPhone.

El teléfono de Apple incluía el dispositivo táctil, la navegación por internet y otras aplicaciones de servicios.

Aquello cambió por completo el concepto de “teléfono móvil”: ya no solo servía para llamar o enviar mensajes, sino que podía hacer muchísimas cosas más. En 2010, prácticamente todos los smartphones tenían pantalla táctil y conectividad a internet.

Muchos modelos y muchas marcas irrumpieron en el mercado tecnológico siguiendo la estela del iPhone. Pasamos de usarlo para llamar a no despegarnos del móvil en todo el día.

El mundo del teléfono móvil está en constante cambio y evolución. Las últimas novedades incluyen los smartwatches o relojes inteligentes conectados al móvil, las pantallas curvas o los dispositivos resistentes al agua.

El Mobile World Congress ofrece la oportunidad de ver todas las novedades de un invento que nació para conectar a las personas y ahora forma parte de nuestra vida a todas horas.

Computadora

El Ábaco

Fue inventada en Babilonia unos 500 anos antes de Cristo, los ábacos antiguos eran tableros para contar, no eran una computadora porque no tenían la capacidad para almacenar información, pero con este instrumento se realizaban transacciones en diversas ciudades de la antigüedad. Actualmente se pueden realizar operaciones como multiplicación y división en los ábacos y son muy usados en China.

Calculadora de Pascal

En 1642 por el joven francés BLAISE PASCAL al ver que su padre tenia problemas para llevar una correcta cuenta de los impuestos que cobraba inventa una maquina calculadora que trabajaba a base de engranajes, la misma que Pascal la llamo con en nombre de PASCALINA.

Maquina de Multiplicar de Leibniz

Gottfried Wilhelm von Leibniz agrega a la maquina inventada por Blaise Pascal las funciones de multiplicación y división.

Maquina de Telar de Jacquard

En 1801 el Francés Joseph Marie Jacquard inventa una máquina de telar. Una de las ventajas es que por atravesar de tarjetas perforadas la maquina era capaz de crear diferentes patrones en las telas. Las tarjetas perforadas contenían orificios, los cuales la maquina era capaz de leer y así efectuar el tipo de patrón que se le había indicado. Esto quiere decir que se había inventado el almacenamiento por medio de las tarjetas perforadas los cuales ahora conocemos como discos. Las tarjetas perforadas fueron el inicio de poder almacenar información por medio de los orificios.

Charles Xavier Thomas de Colmar (1820)

Inventó una calculadora que podía llevar a cabo las cuatro operaciones matemáticas básicas (sumar, restar, dividir y multiplicar).

Máquina diferencia y analítica de Babbage (1822)

En1822 Charles Babbage creo una maquina diferencial capaz de desarrollar polinomios pero varios inconvenientes en las piezas de esta maquina hicieron que fracasara, luego de este fracaso en 1833 Babbage crea la maquina analítica la cual era capaz de hacer todas las operaciones matemáticas y ser programada por medio de tarjetas de cartón perforado y guardar una enorme cantidad de cifras, es por esto que a Charles Babbage se le considera el padre de la informática.

Máquina tabuladora de Hollerith (1889)

Entre los años 1880 y 1890 se realizaron censos en los estados unidos, los resultados del primer censo se obtuvieron después de 7 años, por lo que se suponía que los resultados del censo de 1890 se obtendrían entre 10 a 12 años, es por eso que Herman Hollerith propuso la utilización de su sistema basado en tarjetas perforadas, y que fue un éxito ya que a los seis meses de haberse efectuado el censo de 1890 se obtuvieron los primeros resultados, los resultados finales del censo fueron luego de 2 años, el sistema que utilizaba Hollerith ordenaba y enumeraba las tarjetas perforadas que contenía los datos de las personas senadas, fue el primer uso automatizado de una maquina. Al ver estos resultados Holerith funda una compañía de maquinas tabuladoras que posteriormente paso a ser la International Business Machines (IBM).

Primera generación del computador

La primera generación de computadoras comprende desde el año 1944 a 1956, en esta primera generación se da la creación de la computadora MARK I que fue desarrollada por Howard Aiken, en este periodo se desarrolla la segunda guerra mundial motivo por el cual muchos proyectos quedaron inconclusos, pero también hubieron proyectos impulsados por este mismo motivo que fue la guerra, que hizo que se logren grandes desarrollos, es asi como se crea la computadora ENIAC (Electronic Numerical Intregrator and Calculator) que era una enorme computadora la cual ocupaba mas de una habitación, pesaba mas de 30 toneladas y trabajaba con mas de 18 mil tubos de vació, una de sus características importantes fue que usaba el sistema binario en lugar del sistema decimal, luego fue construida por Eckert y Mauchley la computadora EDVAC (Electronic, Discrete Variable Automatic) que contaba con un programa, este programa le permitía al computador alternar las operaciones dependiendo de los resultados obtenidos previamente.

UNIVAC I

Es de mencionar que durante esta primera generación lo mas importante de las computadoras que se crearon fue el uso de tubos al vacío, ademas cabe mencionar que después de 1950 se crearon diversas maquinas cada una con un avance significativo, en 1951 se construyó la primera computadora para uso comercial la cual fue llamada UNIVAC I, esta computadora fue construida para ser usada en la oficina de censos de los Estados Unidos.

Una de las compañías que no dejo de producir computadoras fue IBM la cual en el año de 1953 construyó su computador 701 y posteriormente el 752.

SEGUNDA GENERACIÓN DEL COMPUTADOR

La segunda generación comprende desde los años 1959 a 1964, lo mas destacable de esta segunda generación es el reemplazo del uso de tubos al vacío por los transistores, lo que hizo que las computadoras sean mas pequeñas y más rápidas.

En esta segunda generación se reemplazo el lenguaje de máquina por el lenguaje ensamblador, se crearon lenguajes de alto nivel como el COBOL y el FORTRAN. Además para el almacenamiento de la información se comenzaron a usar cintas magnéticas.

Aunque en esta generación se disminuyó el tamaño y se aumento la velocidad, aun las computadoras significaban un considerable costo para las empresas.

TERCERA GENERACIÓN DEL COMPUTADOR

Esta generación comprende desde 1964 a 1971 y el mayor logro de esta generación es el uso de circuitos integrados (chips de silicio), esto hizo que las computadoras sean mas pequeñas y mas rápidas, ademas consumían menos electricidad lo que hacia que generen menos cantidad de calor, ademas eran mas eficientes.

Con el uso del chip se dio un enorme paso en la era de la computación ya que el chip contenía una serie de circuitos integrados los cuales almacenaban la información, esto permitió que las computadoras puedan hacer varias tareas a la vez como era la de procesamiento de información y calculo matemático.

En la tercera generación comienzan a surgir los programas o software, la compañía que tuvo su apogeo en esta generación fue IBM la cual lanzó al mercado las minicomputadoras IBM 360 y 370.

CUARTA GENERACIÓN DEL COMPUTADOR

La cuarta generación de las computadoras se da desde 1971 a 1981, lo más importante en esta generación es el invento del microprocesador el cual unía los circuitos integrados en un solo bloque. La creación del microprocesador hizo posible el desarrollo de las computadoras personales o PC, lo cual marcaría una revolución en el mundo de la computación, esto cambiaría la forma de trabajar e incluso de vivir de muchas personas hasta la actualidad.

En el año de 1971 la compañía INTEL crea el primer chip de 4 bits, el cual contenía una gran cantidad de transistores.

Esta generación de computadores aparecen las primeras microcomputadoras las cuales fueron fabricadas por la compañía APPLE e IBM.

QUINTA GENERACIÓN DEL COMPUTADOR

La quinta generación se sitúa entre los años 1982 a 1989, en estos años las empresas encargadas de construir computadoras contaron con grandes avances de microelectrónica y en avances de software, es en este periodo cuando surge la “red de redes” o Internet, y es ahí donde se dan los mas grandes avances, se da inicio a la inteligencia artificial, que tenia el propósito de equipar a las computadoras con la capacidad de razonar para encontrar soluciones a sus propios problemas siguiendo patrones y secuencias, estas computadoras podían operar en grandes compañías como es la construcción de automóviles, y otras que podrían hacer diversas tareas y a un ritmo impresionante.

Aparecen las computadoras portátiles, además las grandes computadoras podían trabajar en procesos en paralelo que era el trabajo de la computadora por medio de varios microprocesadores cada uno realizaba un trabajo distinto.

Los dispositivos de almacenamiento de información surgen un cambio pudiendo ahora almacenar mayor cantidad de información, se lanza al mercado el CD como estándar para el almacenamiento de música y vídeo.

SEXTA GENERACIÓN DEL COMPUTADOR

Se viene dando a partir de 1990 hasta la fecha, en estos últimos años hemos venido viendo que las computadoras ahora son mas pequeñas, son mas versátiles, ahora Internet es una herramienta indispensable tanto en los centros de labores como en el hogar, casi el 90% de la población hace uso en algún momento de Internet, y por consiguiente de una computadora.

Ahora vemos que el costo de una PC es relativamente bajo así como el de una Laptop, las computadoras de ahora vienen trabajando con arquitecturas paralelas / vectoriales lo que hace que sean muy rápidas, pueden almacenar una cantidad enorme de información hablamos de terabites, ahora las computadoras prácticamente toman decisiones propias alcanzando casi la misma del ser humano, tenemos computadoras táctiles que casi no ocupan espacio en el hogar y el trabajo, también con diseño holográfico, lo cual ha revolucionado el mercado de la informática.

[danilodiazgranadosmanglano]

Danilo Díaz Granados recomienda: Los 13 tipos de funciones matemáticas (y sus características)

Las matemáticas son una de las disciplinas científicas más técnicas y objetivas que existen. Es el principal marco a partir del cual otras ramas de la ciencia son capaces de realizar mediciones y operar con las variables de los elementos que estudian, de tal manera que además de una disciplina en sí misma supone junto a lo lógica una de las bases del conocimiento científico. Pero dentro de las matemáticas se estudian procesos y propiedades muy diversos, estando entre ellos la relación entre dos magnitudes o dominios vinculados entre sí, en el que uno resultado concreto se obtiene gracias o en función del valor de un elemento concreto. Se trata de la existencia de funciones matemáticas, las cuales no siempre van a tener una misma manera de afectarse o relacionarse entre sí. Es por ello que **podemos hablar de diferentes tipos de funciones matemáticas**, de los cuales vamos a hablar a lo largo de este artículo. * Artículo relacionado: "[14 acertijos matemáticos (y sus soluciones)](/cultura/acertijos-matematicos)" ## Funciones en matemáticas: ¿qué son? Antes de pasar a establecer los principales tipos de funciones matemáticas que existen resulta de utilidad hacer una pequeña introducción de cara a dejar claro de qué estamos hablando cuando hablamos de funciones. Las funciones matemáticas se definen como **la expresión matemática de la relación existente entre dos variables o magnitudes**. Dichas variables son simbolizadas a partir de las últimas letras del alfabeto, X e Y, y reciben respectivamente el nombre de dominio y codominio. Dicha relación se expresa de tal modo que se busca la existencia de una igualdad entre ambos componentes analizados, y en general implica que para cada uno de los valores de X existe un único resultado de Y y viceversa (aunque existen clasificaciones de funciones que no cumplen con este requisito). Asimismo, esta función **permite la creación de una representación en forma de gráfica** que a su vez permite la predicción del comportamiento de una de las variables a partir de la otra, así como posibles límites de esta relación o cambios de comportamiento de dicha variable. Tal y como ocurre cuando decimos que algo depende de o está en función de otro algo (por poner un ejemplo, si consideramos que nuestra nota en el examen de matemáticas está en función del número de horas que estudiemos), cuando hablamos de una función matemática estamos indicando que la obtención de un valor determinado depende del valor de otro vinculado a él. De hecho, el propio ejemplo anterior es directamente expresable en forma de función matemática (si bien en el mundo real la relación es mucho más compleja ya que en realidad depende de múltiples factores y no solo del número de horas estudiadas). ## Principales tipos de funciones matemáticas A continuación os mostramos algunos de los principales tipos de funciones matemáticas, clasificadas en diferentes grupos **según su comportamiento y el tipo de relación que se establece entre las variables X e Y**. ### 1. Funciones algebraicas Se entienden por funciones algebraicas el conjunto de tipos de funciones matemáticas caracterizadas por establecer una relación cuyos componentes son o bien monomios o bien polinomios, y **cuya relación se obtiene a través de la realización de operaciones matemáticas relativamente simples**: suma resta, multiplicación, división, potenciación o radicación (uso de raíces). Dentro de esta categoría podemos encontrar numerosas tipologías. #### 1.1. Funciones explícitas Se entienden por funciones explícitas todos aquellos tipos de funciones matemáticas cuya relación se puede obtener de forma directa, simplemente sustituyendo el dominio x por el valor que corresponda. Dicho de otra manera, es la función en que directamente **encontramos una igualación entre el valor de y una relación matemática en la que influye el dominio x**. #### 1.2. Funciones implícitas Al contrario que en las anteriores, en las funciones implícitas la relación entre dominio y codominio no se establece de manera directa, siendo necesario realizar diversas transformaciones y operaciones matemáticas con el fin de encontrar la manera en que x e y se relacionan. #### 1.3. Funciones polinómicas Las funciones polinómicas, en ocasiones entendidas como sinónimas de las algebraicas y en otras como una subclase de estas, integran el conjunto de tipos de funciones matemáticas en las que **para obtener la relación entre dominio y codominio es necesario realizar diversas operaciones con polinomios** de diverso grado. Las funciones lineales o de primer grado son probablemente el tipo de función más sencilla de resolver y se encuentra entre las primeras que se aprenden. En ellas simplemente existe una relación simple en que un valor de x va a generar un valor de y, y su represantación gráfica es una recta que ha de cortar el eje de coordenadas por algún punto. La única variación va a ser la pendiente de dicha recta y el punto en que corte el eje, manteniéndose siempre el mismo tipo de relación. Dentro de ellas podemos encontrar las funciones identidad, **en las que directamente se da una identificación entre dominio y codominio** de tal manera que ambos valores son siempre el mismo (y=x), las funciones lineales (en que únicamente observamos una variación de la pendiente, y=mx) y las funciones afines (en que podemos encontrar alteraciones en el punto de corte del eje de abscisas y la pendiente, y=mx+a). Las funciones cuadráticas o segundo grado son aquellas que introducen un polinomio en que una única variable tiene un comportamiento no lineal a lo largo del tiempo (mejor dicho, en relación con el codominio). A partir de un límite concreto la función tiende a infinito en uno de los ejes. La representación gráfica se establece como una parábola, y matemáticamente se expresa como y=ax2+bx+c. Las funciones constantes son aquellas en las que **un único número real es el determinante de la relación entre dominio y codominio**. Es decir, no existe una variación real en función del valor de ambos: el codominio siempre va a ir en función de una constante, no existiendo una variable de dominio que pueda introducir cambios. Simplemente, y=k. * Quizás te interese: "[Discalculia: la dificultad a la hora de aprender matemáticas](/clinica/discalculia)" #### 1.4. Funciones racionales Se denominan como funciones racionales al conjunto de funciones en las que el valor de la función se establece a partir de un cociente entre polinomios diferentes de cero. En dichas funciones el dominio incluirá todos los números excepto los que anulen el denominador de la división, los cuales no permitirían obtener un valor y. **En este tipo de funciones aparecen límites conocidos como asíntotas**, los cuales precisamente serían aquellos valores en los que no habría un valor de dominio o codominio (es decir cuando y o x son igual a 0). En dichos límites, las representaciones gráficas tienden a infinito, sin tocar jamás dichos límites. Un ejemplo de este tipo de función: y= √ ax #### 1.5. Funciones irracionales o radicales Reciben el nombre de funciones irracionales el conjunto de funciones en las cuales una función racional aparece introducida dentro de un radical o raíz (que no tiene porqué ser cuadrada, ya que es posible que sea cúbica o con otro exponente). Para poder resolverla **habrá que tener en cuenta que la existencia de dicha raíz nos impone ciertas restricciones**, como por ejemplo el hecho de que los valores de x siempre van a tener que provocar que el resultado de la raíz sea positivo y mayor o igual a cero. #### 1.6. Funciones definidas a trozos Este tipo de funciones son aquellas en las que el valor de y cambia el comportamiento de la función, existiendo dos intervalos con un comportamiento muy diferente en base al valor del dominio. Existirá un valor que no formará parte de este, el cual será el que valor a partir del cual el comportamiento de la función difiera. ### 2. Funciones trascendentes Se denominan funciones trascendentes aquellas representaciones matemáticas de relaciones entre magnitudes que no pueden obtenerse a través de operaciones algebraicas, y para las que **es necesario realizar un complejo proceso de cálculo con el fin de obtener su relación**. Incluye principalmente aquellas funciones que requieren del uso de derivadas, integrales, logaritmos o que tienen un tipo de crecimiento que va creciendo o decreciendo de manera continuada. #### 2.1. Funciones exponenciales Tal y como indica su nombre, las funciones exponenciales son el conjunto de funciones que establecen una relación entre dominio y codominio en la que se establece una relación de crecimiento a nivel exponencial, es decir que existe un crecimiento cada vez más acelerado. el valor de x es el exponente, es decir la manera en que **el valor de la función va variando y creciendo a lo largo del tiempo**. El ejemplo más sencillo: y=ax #### 2.2. Funciones logarítmicas El logaritmo de cualquier número es aquel exponente el cual será necesario elevar la base empleada con el fin obtener el número concreto. Así pues las funciones logarítmicas son aquellas en las que estamos empleando como dominio el número que se ha de obtener con con una base concreta. **Se trata del caso opuesto e inverso de la función exponencial**. El valor de x ha de ser siempre superior a cero y distinta de 1 (ya que cualquier logaritmo con base 1 es igual a cero). El crecimiento de la función es cada vez menor según va aumentando el valor de x. En este caso y=loga x #### 2.3. Funciones trigonométricas Un tipo de función en el que se establece la relación numérica entre los diferentes elementos que configuran un triángulo o una figura geométrica, y concretamente las relaciones que existen entre los ángulos de una figura. Dentro de estas funciones encontramos el cálculo del seno, coseno, tangente, secante, cotangente y cosecante ante un valor x determinado. ## Otra clasificación El conjunto de tipos de funciones matemáticas anteriormente explicadas tienen en cuenta que para cada valor del dominio se corresponde un único valor del codominio (es decir cada valor de x va a provocar un valor concreto de y). Sin embargo, y aunque este hecho suele considerarse básico y fundamental, lo cierto es que es posible encontrar algunos **tipos de funciones matemáticas en que puede haber cierta divergencia en lo que a correspondencias entre x e y se refiere**. Concretamente podemos encontrar los siguientes tipos de funciones. ### 1. Funciones inyectivas Reciben el nombre de funciones inyectivas aquel tipo de relación matemática entre dominio y codominio en el que cada uno de los valores del codominio se vincula únicamente a un valor del dominio. Es decir, x solo va a poder tener un único valor para un valor y determinado, o bien puede no tener valor (es decir un valor concreto de x puede no tener relación con y). ### 2. Funciones suryectivas Las funciones suryectivas son todas aquellas en las que **todos y cada uno de los elementos o valores del codominio (y) están relacionados con al menos uno del dominio (x)**, aunque pueden ser más. No tiene porqué ser necesariamente inyectiva (al poder asociarse varios valores de x a un mismo y). ### 3. Funciones biyectivas Se denomina como tal al tipo de función en que se dan propiedades tanto inyectivas como suryectivas. Es decir, **hay un único valor de x para cada y**, y todos los valores del dominio se corresponden con uno del codominio. ### 4. Funciones no inyectivas y no suryectivas Este tipo de funciones indican que existen múltiples valores del dominio para un codominio concreto (es decir diferentes valores de x nos van a dar una misma y) a la par que otros valores de y no se encuentran vinculados a ningún valor de x. #### Referencias bibliográficas: * Eves, H. (1990). Foundations and Fundamental Concepts of Mathematics (3 edición). Dover. * Hazewinkel, M. ed. (2000). Encyclopaedia of Mathematics. Kluwer Academic Publishers. Ver Fuente Ver Fuente

[tocho17-blog]

Polinomios, trinomios y binomios

Polinomios. En matemáticas, un polinomio ​​​ es una expresión algebraica constituida por una suma finita de productos entre variables y constantes. Las variables pueden tener exponentes de valores definidos naturales incluido el cero y cuyo valor máximo se conocerá como grado del polinomio.

El valor numérico de un polinomio lo que resulta sustituir la variable x por el número asignado a ella y efectuar las operaciones indicadas a la expresión del polinomio y su valor. Trinomios.

MATEMÁTICAS

1.Expresión algebraica formada por la suma o la diferencia de tres términos o monomios.

2.Conjunto de tres personas o cosas tomadas como unidad o como elementos en equilibrio o dependientes unos de otros.

Un trinomio es una expresión algebraica formada por tres términos o dos monomios separados por el signo + o - . Binomios.

1.MATEMÁTICAS

Expresión algebraica formada por la suma o la diferencia de dos términos o monomios.

"a + b es un binomio"

2.

Conjunto de dos personas o cosas tomadas como unidad o como elementos en equilibrio o dependientes uno de otro.

"el binomio cuerpo-espíritu; el mundo moderno gira en torno al binomio información + comunicación"

Un binomio es una expresión algebraica formada por dos términos o dos monomios separados por dos signos

[homeworkitsup-blog]

Glosario de la asignatura Matemática

A

Adición

Operación matemática en la que se unen dos o más cantidades.

Aleatorio

Que tiene cierta posibilidad de suceder.

Álgebra

Rama de la Matemática en la que se usan símbolos, letras y números para expresar relaciones entre expresiones que representan números

Algoritmo

Descripción paso a paso de una solución de un problema

Altura de un paralelogramo

Es la longitud del segmento de recta perpendicular a la base del paralelogramo, entre ésta y el lado opuesto.

Altura de un triángulo

Longitud del segmento de recta perpendicular a la base, comprendido entre ésta y el vértice opuesto.

Amplificar una fracción

Es obtener una fracción equivalente a la original, multiplicando su numerador y su denominador por un mismo número.

Amplitud de un conjunto de datos

Es la diferencia entre el dato mayor y el menor.

Ángulo

Es una figura formada por dos rayos con un punto final común.

Ángulo agudo 

Es cualquier ángulo cuya medida es entre 0° y 90°

Ángulo central

Ángulo cuya vértice es el centro de una circunferencia.

Ángulos complementarios

Dos ángulos complementarios si la suma de sus medidas es 90°.

Ángulo de depresión

Si una persona está viendo hacia abajo, entonces el ángulo formado por la horizontal a la línea recta de visión se llama ángulo de depresión.

Ángulo de elevación

Si una persona está mirando hacia arriba, entonces el ángulo de la horizontal a la línea recta de visión se llama ángulo de elevación.

Ángulo de rotación 

Es la medida del ángulo que describe un movimiento de giro alrededor de un centro dado.

Ángulo inscrito

Ángulo cuyo vértice está en la circunferencia y sus lados contienen cuerdas de la circunferencia.

Ángulos internos de un polígono

Son los ángulos situados en el interior del polígono y cuyos vértices son los vértices del polígono y cuyos lados del polígono que convergen en cada vértice.

Ángulo llano

Es el ángulo que mide 180°.

Ángulo obtuso

Es cualquier ángulo cuya medida es entre 90° y 180°.

Ángulo recto

Es el ángulo que mide 90°.

Ángulo reflejo

Es cualquier ángulo cuya medida es mayor de 180°.

Ángulos suplementarios

Dos ángulos suplementarios si la suma de sus medidas es 180°.

Área

Es la medida de un espacio biodimensional.

Área superficial

Área de la superficie de un sólido.

Arista de un poliedro

Es un segmento rectilíneo en el que se encuentran dos caras del poliedro.

Aritmética

Es la parte de la Matemática que estudia los números y las operaciones hechas con ellos.

Asociativa (propiedad)

Una operación * cumple la propiedad asociativa en un conjunto dado A, si para cualquiera elemento a, b y c de A, se tiene que (a * b) * c = a* (b * c)

Axioma

Proposición aceptada sin demostración.

B

Baricentro

Es el punto donde se cortan las medianas de un triángulo.

Base de un paralelogramo

Es cualquiera de sus lados.

Base de un trapecio

Es cualquiera de sus lados paralelos.

Base de un triángulo

Es cualqueira de sus lados.

Binomio

Polinomio que consta exactamente de dos términos.

Bit

La más pequeña unidad de información, es igual a 0 o a 1.

Byte

Unidad de información igual a 8 bits.

C

Capacidad

Es la medida de la cantidad de líquido, gas o sólido que un recipiento puede contener.

Cara de un poliedro

Es cada uno de los polígonos que lo limitan.

Círculo

Región del plano contenida por una circunferencia.

Clasificar

Agrupar elementos de acuerdo con determinadas características.

Circunferencia

Es un conjunto de todos los puntos que están a una distancia fija de un punto llamado centro.

Combinaciones

Son listas en las que el orden no es importante.

Conmutatita (propiedad)

Una operación * cumple la propiedad conmutativa en un conjunto dado A, si para cualquiera elemento como a y b, se tiene que a * b = b * a.

Cuadrilátero

Polígono de cuatro lados.

Cuartil

Uno de los tres nújmeros que divide un conjunto de datos.

Cubo

Es un prisma rectangular en el que todas sus caras son cuadrados congruentes.

Cuerda de una circunferencia

Es un segmento de recta que une dos puntos de la circunferencia.

D

Diagonal de un polígono

Es un segmento de recta que une dos vértices no contiguos del polígono.

Diagrama de dispersión

Gráfica que se puede usar para examinar la posible relación entre dos variables.

Diagrama de Venn

Es una representación pictórica de dos o más conjuntos que muestran elementos de los conjuntos tiene en común y los que pertenecen a uno u otro conjunto.

Diámetro de una circunferencia

Es un segmento de una recta que une dos puntos de la circunferencia y pasa por su centro.

Dígito

Es cada uno de los símbolos que se usan para escribir números en el sistema de base 10. Los dígitos son: 0,1, 2, 3, 4, 5, ,6 ,7, 8, 9.

Dilatación de la figura

Es la transformación de la figura en la que se modifica su tamaño sin cambiar su forma.

Distancia entre dos puntos 

Es la longitud del segmento rectilíneo que une dichos puntos.

Divisible

Una cantidad m es divisible entre otra cantidad n si m contiene a n un número exacto de veces. Por ejemplo 12 es divisible entre 3 porque 12 dividido entre 3 es 4.

División

Es una operación matemática, la operación inversa de la multiplicación, que consiste en la partición o separación de elementos de un conjunto en subconjuntos de un número fijo de elementos.

E

Eje de simetría

Una línea recta es un eje de simetría de una figura plana, si al doblar la figura en dos, según esa línea, las dos partes coinciden en todos sus puntos.

Ejercicio

En el contexto de la Matemática, un ejercicio es una pregunta con la que el estudiante ya se ha encontrado y para cuya resolución tiene un algoritmo o técnica.

Ecuación

Es una declaración de que dos números o expresiones matemáticas son iguales.

Elipse

Es una curva cerrada con exactamente dos líneas de simetría.

F

Factores

Dos números a y b son factores de otro número c, si c= a x b

Figura abierta

Es una figura con puntos finales que no se encuentran.

G

Geometría

Es la rama de la Matemática que estudia las propiedades y las medidas de las figuras en el plano o en el espacio.

Gráfica

Es un dibujo o diagrama que se utiliza para dar información.

[mates3-blog]

http://racoderecursos.blogspot.com.es/p/matematiques.html

MATEMÀTIQUES

Activitats variades per a fer online.

Angles

Angles, mesurar.

Ángulos: apuntes para imprimir

Ángulos, medir.

Arrodonir a les desenes

Arrodonir a les centenes

Càlcul mental

Càlcul mental

Càlcul mental: sumes i restes

Càlcul mental: dividir entre 2, 3 i 4

Càlcul mental: Joc molt divertit

Cálculo de la mitad, tercio y cuarto

Cálculo de la mitad, tercio y cuarto

Cálculo de la mitad, tercio, cuarto y quinto

Confecció d'un tangram

Conjunto de webs relacionadas con las matemáticas

Construir juegos matemáticos. Material para imprimir.

Decimals. Conjunt de diferents webs

Decimals

Decimals

Decimales, cómo leerlos.

Descarga de ejercicios variados

Dividir per la unitat seguida de zeros

Dividir por la unidad seguida de ceros

Divisió entera

Divisió de dues xifres

Divisió de tres xifres

Divisiones: decimal entre decimal

Divisiones: decimal entre natural

Divisiones: natural entre decimal

Divisions

Divisions

Divisions amb resta

Divisions mitjançant un joc

Divisions, visualitzant-les des de les taules de multiplicar

Divisions raonades per grups (editorial Teide)

Divisiones

Doble i triple

Ecuaciones de 2º grado y sistemas

Ejercicios para Primaria  

Ejercicios nivel ESO

Ejercicios para ciclo superior ESO

Ejercicios para imprimir de decimales.

Ejercicios resueltos/ESO y Bachillerato

Ejercicios variados de primaria

Ejercicios variados/ESO y Bachillerato

Ejercicios varios de matemáticas de primaria

El quinzet

El quinzet. Jclic de problemes i exercicis

El quinzet. Material de càlcul global

Enllaç amb webs que diposen de materials multimèdia

Equacions

Estadística: crear gràfiques en línia

Estadística: hacer histogramas en línea

Estimar

Explicaciones para ESO

Fichas de cálculo para imprimir y más cosas

Fracciones. Fichas para imprimir

Fracciones, (anglès)

Fracciones.

Fracciones equivalentes

Fracciones

Fracciones 2

Fracción de un número decimal

fracciones: Conceptos y ejercicios.

Fraccions: L'ull d'Horus (problema)

Funciones

Funciones (hotpotatoes)

Funciones lineales (webquest)

Funciones lineales.

Funciones: Apuntes y ejercicios

Funciones: apuntes y ejercicios (pdf)

Función lineal

Generedaor d'exercicis on line amb diferents idiomes i molts nivells

Generador de divisions

Generador de ejercicios: problemas, multiplicaciones y divisiones

Generador de ejercicios: problemas, multiplicaciones y divisiones

Generador de multiplicacions

Generador d'operacions

Generador de sumes i restes

Geometría para a infantil

Geometría: reconocimiento de figuras (infantil y inicial)

Geometria dinámica. GES y Bachillerato

Geometria plana

Geometría

Geometría: problemas en pdf

Geoplano:ejercicios

Geoplano: juegos

Història de les matemàtiques

Infogramas de diversos temas matemáticos

Juegos de memoria, lógica, observación y solitarios

Jocs matemàtics en general

Juegos matemáticos

Juegos matemáticos II

Juegos matemáticos III

Juegos matemáticos IV

Juegos matemáticos V

Juegos matemáticos VI

Juegos matemáticos0

Juegos matemáticos sencillos

Juegos matemáticos para Primaria

Juegos y muchas más cosas para CS de Primaria y ESO

Jugar a enfonsar la flota estudiant les taules

Juguem al tres en ratlla i estudiem taules

Joc  per multiplicar

Matemáticas de Primaria

Matemàtiques amb ordinador per a Batxillerat

Material para imprimir muy variado e interesante.

Mates de 5º de primaria

Mecànica de la divisió

Mesurar angles

Medidas de longitud, masa y capacidad

Medidas de tiempo

Mets ESO: Responder ejercicios de hotpotatoes

Multiplicaciones divertidas

Multiplicaciones por la unidad seguida de ceros

Múltiplos y divisores: apuntes y ejercicios

Numeración

Números enteros

Nombres enters: major, menor o igual

Operaciones aritméticas on line

Operacions bàsiques

Operaciones

Parèntesis: sumes i restes

Parèntesi: Operacions en general

Pentonimos:ejercicios

Pentonimos: Ejercicios 2.

Polinomios

Porcentajes

Practicar divisions de dues xifres.

Problemes de sumes i restes

Problemas y acertijos

Problemas mentales

Problemes visuals

Proporciones y porcentajes

Propostes de diferents proves matemàtiques

Prova de la resta

Pruebas y exámenes/ESO

Recreacions matemàtiques. Jocs i activitats.

Recull d'activitats molt variades de matemàtiques.

Recursos generals de mates per primària i secundària

Recursos matemàtics

Recursos matemàtics variats

Recursos matemàtics

Recursos matemàtics varis

Recursos matemáticos de todo tipo

Recursos matemáticos muy variados e interesantes

Restas de forma divertida

Sèries amb figures geomètriques

Sistemes d'equacions (curs moodle)

Suma de decimales

Sumas de forma divertida

Tangram:Ejercicios interactivos

Tangram: Ejercicios interactivos2

Tangram: Figures per imprimir

Tangram interactivo

Tangram: Material para ver o imprimir

Taules de multiplicar

Taules de multiplicar

Taules de multiplicar

Taules de multiplicar

Taules de multiplicar

Taules de multiplicar: control de rapidesa

Taules de multiplicar: molts recursos i variats

Unidades didácticas de ESO

Unidad seguida de ceros: explicación y ejercicios.

Unitat seguida de zeros: multiplicacions i divisions

Usa el coco. Razonamiento online divertidos.

Video de estimación de las medidas.

Videos matemàtics

[totumat]

Operaciones entre polinomios

Podemos definir las operaciones de suma, resta, multiplicación y división entre polinomios como una generalización de las operaciones que hemos definido entre los números reales.

Podemos definir las operaciones de suma, resta, multiplicación y división entre polinomios como una generalización de las operaciones que hemos definido entre los números reales. Suma de polinomios Para sumar o restar polinomios, recurrimos a la propiedad asociativa de los números reales, pues agrupamos los sumandos que tengan la misma potencia de como factor, de forma que si consideramos dos…