#Linear Inequalities assignments | Explore Tumblr posts and blogs

lipshits-continuous · 9 months ago

Text

Topological Spaces 1: Introduction and Metric Spaces

Welcome to the first of several posts about general topology! The goal of these posts is to give an overview and introduction to key concepts in topology. I will try to give intuitions about definitions and results so that even if you're not as aquainted with formal mathematics you can still get something from this. Whilst there aren't any prerequisties per say (for the reason above), for those who are interested in the moral formal aspects it will be helpful to be familiar with real analysis. Some familiarity with linear algebra is also helpful in this post though probably won't play a role going forward.

Topology is such a broad subject that assigning one goal is quite hard. One early goal is to generalise the notion of continuity and other familiar notions, which we shall do. Topology certainly doesn't stop there. One large goal is to find properties which are invariant under homeomorphism (bijective continuous maps whose inverse is also continuous). We shall see some examples of this as we go further!

The goal of this post is to give context to the definitions of topological spaces and continuity via the study of metric spaces. The definition of a topological space can seem quite dry and like it's been plucked out of thin air when just presented without motivation. In this sense, metric spaces are the bridge between familiar concepts in real analysis and the more general setting of topology.

1.1: Metric Spaces:

As the name might suggest, metric spaces are sets with an appropriate notion of distance between points in the set. For the real numbers, we have an intuitive sense of distance between two numbers: the absolute value of their difference. From this, we can immediately get three desirable properties we'd want a notion of distance to have:

Positivity: |x-y|≥0

|x-y|=0 if and only if x=y

Symmetry: |x-y|=|y-x|.

These are desirable because this says, in order, that distance is always positive, two points are the same only when the distance between then is 0, and the distance beween x and y is the same as the distance between y and x.

The last property is not as immediately obvious from the definition but is still a fairly intuitive property that we'd expect a notion of distance to have: the triangle inequality. Formally, for any x,y, and z real number we have |x-y|≤|x-z|+|z-y|. This just says that the distance between two points is always shorter than the distance achieved by adding an intermediate point. The name comes from visiualising this with lengths of a triangle! The proof that this holds for the absolute value can be found here.

You might ask whether there are any more properties we'd like but it turns out that this is enough to generalise a lot of concepts in real analysis in an appropriate way. That is, we still maintain a lot of nice results without requiring too many rules. So let us finally see the definition!

Definition 1.1:

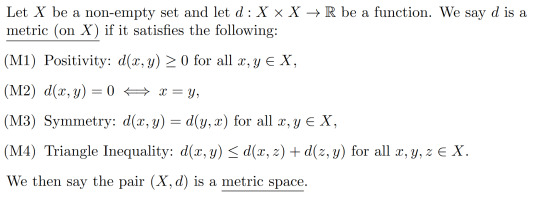
Note: It's common to combine the first two axioms together but for the sake of clarity, I have separated them.

Examples 1.2:

The details of why each of these is a metric can be found in this post.

A result of the second example is that metric spaces are also an appropriate generalisation of normed vector spaces. The fact they are a generalisation is seen from the fact that the discrete metric cannot be seen as the result of a norm and isn't restricted to vector spaces.

1.2: Continuity:

Intuitively, continuous functions are ones that don't have gaps or sudden jumps. In the case of functions from the real numbers to itself, we can view this as "we can draw its graph without lifting the pencil". This can be restated as "points that are close to each other remain close to each other after the function is applied". But how does one formalise "closeness"? With distances of course!

Definition 1.3:

Remark: Continuity departs on the metrics. A function that is continuous in one metric isn't necessarily continuous in another.

Examples 1.4:

Now I'd like to prove a fairly common result to further demonstrate continuity.

Proposition 1.5:

1.3: Open Sets in Metric Spaces

Now we shall see the first aspects of topology creeping in. One way to think about open sets which don't have any points "at the edge". This is immediately clear in the definition we will give below but when we generalise the notion of an open set, we will seemingly lose this. However, we will see that this intuition will still hold!

Definition 1.6:

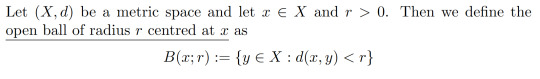
Example 1.7:

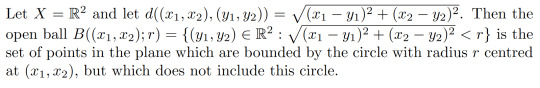
We will now define the notion of an open set using these open balls.

Definition 1.8:

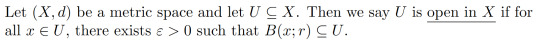
This does indeed formalise "no points at the edge" since for open sets, all points close enough to x are always in U.

Remark: Openness depends on the metric. For example, {0} is open in the real numbers with the discrete metric but not with the absolute value metric.

Now, "open ball" would be a silly name for it if they weren't indeed open in the sense of definition 1.8 but luckily they are!

Proposition 1.9:

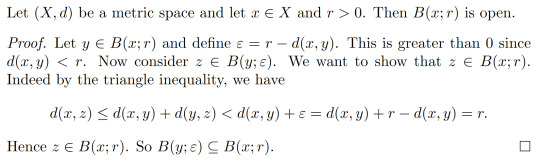
Example 1.10:

Open intervals of real numbers are indeed open with respect to the absolute value. If we have the open interval I=(a,b) for finite a<b, we may view I as an open ball by setting x=(b+a)/2 and r=|b-a|/2. Then I=B(x;r).

Now we shall prove a very important result about open sets that lets you build new open sets out of old opens but will also be the foundation upon which we generalise the notion of open sets!

Lemma 1.11:

Proof:

Remark: Finiteness is important for 3. If we consider the real numbers with the absolute value metric then (-1/n,1/n) is open for all (non-zero) natural numbers. However their intersection over all n is {0} which is not open in this metric.

Typically, courses would usually talk about closed sets now. However, since the discussion doesn't vary much between metric spaces and topological spaces, we will hold off for now.

1.4: Continuity in terms of open sets

This is a very important step in our journey in generalising continuity. This section with along with the next section will suggest that open sets are actually the structures we'd like to study!

Lemma 1.12:

Before we prove this, I'd like to just comment on why this still alligns with our intution about continuity. The right hand side is saying that points end up close together in Y must've been close together in X.

Remark: It is important to note that U open in X does not necessarily imply f(U) is open in Y when f if continuous. For example, take f(x)=x² in ℝ with its usual notion of continuity, then (-1,1) is open but f((-1,1))=[0,1) which is not open. Maps for which open sets are mapped to open sets are called open maps.

We will see examples of how to use the property on the right hand side in the next post!

1.5: Equivalent Metrics

The goal of this section is to see that sometimes different metrics will give rise to the same open sets!

Definition 1.13:

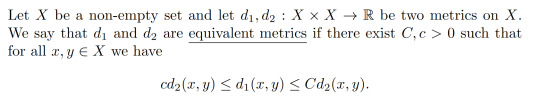
Example 1.14:

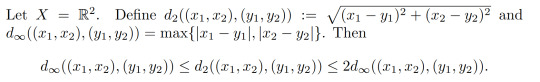
I will omit the details of the proof for brievity. Not that the 2 on the right hand side comes from the fact we're in ℝ² and isn't related to the 2 in the metric.

Remark: Not all metrics are equivalent. The discrete metric and d₂ are not equivalent metrics.

Proposition 1.15:

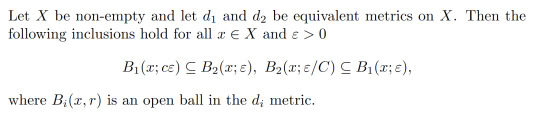
Corollary 1.16:

This ultimately means that some metrics generate the same open sets. Then Lemma 1.12 tells us that equivalent metrics give the same continuous funcitons since we can view continuity in terms of open sets. This suggests that what really matters here is which sets are open. This is what we shall exploit to generalise continuity even further! But that shall have to wait til the next post!

#maths posting #mathblr #maths #mathematics #topology #lipshits posts #long post #undescribed

62 notes · View notes

study-with-aura · 3 months ago

Text

Tuesday, August 20, 2024

I know you all were probably wondering why I didn't post the last three days. No? I plan to tell you anyway. 😊

My brother leaves at the end of the week to go back to university, so I have been spending as much time with him as possible, even if that means we are simply in the same room doing two different things. I can't believe I will have to say goodbye to him again. I know it is for a short time if we compare it to forever, but I love having him at home with me. He and Dad have been doing a lot together as well, which I know Julien looks forward to.

This is a fast update as we must head out so I can get to ballet on time. I hope everyone has a wonderful week! 💛

Tasks Completed:

Algebra 2 - Completed worksheet on applications of linear equations and inequalities

American Literature - copied vocabulary terms + read chapters 10-11 of The Scarlet Letter by Nathaniel Hawthorne + learned about The Bay Psalm Book + read over reflective essay assignment (due 9/20)

Spanish 3 - Reviewed stem-changing verbs in the present tense + completed three graded quizzes (all 10/10)

Bible 2 - Read 2 Samuel 12-13

Early American History - Read about French explorers + looked at maps showing the routes of exploration of NA by the Spanish and the French + answered question on study guide + read "Resisting the European Onslaught" from Civilizations under Siege: The European Conquest of the Americas

Earth Science with Lab - Answered questions about yesterday's reading on the Big Bang utilizing details about the scientific theories and where they fall short

Music Appreciation - Watched a listening guide to Felix Mendelssohn's Violin Concerto + listened to Mendelssohn's Violin Concerto in E minor, Op. 64 (soloist Ray Chen with the Gothenburg Symphony Orchestra and Maestro Kent Nagano)

Khan Academy - Completed US History Unit 2: Lesson 1 (parts 1-3)

Duolingo - Studied for approximately 30 minutes (Spanish + French + Chinese) + completed daily quests

Piano - 60-minute piano lesson + practiced for two hours in one hour split sessions

Reading - Read pages 205-241 of Stateless by Elizabeth Wein

Chores - Laundry

Activities of the Day:

Personal Bible Study (Numbers 30)

Ballet

Pointe

Journal/Mindfulness

#study blog #study inspiration #study motivation #studyblr #studyblr community #study community #study-with-aura

15 notes · View notes

guilibagelz · 1 month ago

Text

my math teacher was bitching that i’m not on the jam board. ts pissing me off. MAYBE i would if edmentum wasn’t assigning some 29 slideshow tutorial glazing linear inequalities

#𓏵 ⟣ ⸝⸝ ⟢ rants and vents #i hate math #fuck math #fuck school #i hate school

1 note · View note

ekalman · 8 months ago

Text

Peer-graded Assignment: Getting Your Research Project Started

Good afternoon, dear reader,

For my Data Visualization course assessment I have chosen working on the dataset provided by GapMinder organization.

After looking at the code book and variables available I decided that I am particularly interested in income rate dependences. Simple questions to answer include the following:

Is higher oil per person associated with higher income per person? If not, how it can be explained?

Is longer life expectancy associated with higher income per person?

How the rates of general/female employment connected to the income rate per person in various countries?

For now I would like to concentrate more on the first question, but I suspect that there will be no linear correlation between oil and income per person. I checked the published articles and there was one that attracted my attention - Does oil drive income inequality? New panel evidence - ScienceDirect. It made me think to include policy score variable into my analysis as well, since average income cannot be a reliable variable if population inequality deepens. I'll need to create countries categorization based on policy score and it will be possible to additionally see the dependency between higher oil per person rate and worse policy scores.

As result, I'd like to determine if average income per person is dependent on oil per person rate taking policy score into consideration. Currently my assumption is that the average income grows with higher oil consumption, but the lower policy score is, the higher income inequality will be.

I prepared a partial code book for my further studies; it is attached below:

Best regards,

Evgenia

1 note · View note

mark007william · 1 year ago

Text

Master Algebra with the Best Algebra Calculator

Algebra, often dubbed the "gateway to higher math," is a foundational subject that plays a crucial role in mathematics education. It serves as a bridge between basic arithmetic and more advanced mathematical concepts. While mastering algebra is essential for success in various fields, it can be a challenging journey for many students. However, the advent of technology has brought forth a valuable tool: the algebra calculator. In this blog, we will explore how you can master algebra with the best algebra calculator at your side.

While algebra calculators serve as fantastic tools for mastering algebra, the guidance and expertise of professionals cannot be understated. My Assignment Help Expert understands the challenges that students face when tackling algebraic concepts and equations. Their team of experienced educators and mathematicians not only provides assistance in algebra but also offers personalized support to help you understand the underlying principles.

The Algebra Conundrum

Algebra is all about using symbols, letters, and numbers to represent and solve real-world problems. It introduces you to essential concepts like equations, inequalities, variables, and functions. Despite its importance, algebra can be intimidating for some, often due to:

Complex Equations: Dealing with equations that involve multiple variables and unknowns can be daunting.

Abstract Notation: The use of abstract symbols, such as "x" and "y," can be confusing, especially when transitioning from straightforward arithmetic.

Problem Solving: Algebra challenges your problem-solving skills, requiring you to apply rules and methods to find solutions.

Conceptual Understanding: Understanding the underlying principles and concepts in algebra is crucial for applying them effectively.

The Role of Algebra Calculators

Algebra calculators, often available as software applications or online tools, provide valuable assistance in your algebraic journey. Here's how they can help you master algebra:

1. Instant Solutions

Algebra calculators offer quick and accurate solutions to algebraic problems. Whether you're dealing with equations, inequalities, or complex algebraic expressions, these tools provide instant results, helping you check your work or find solutions more efficiently.

2. Step-by-Step Guidance

Many algebra calculators offer step-by-step solutions. They break down the problem-solving process, helping you understand how to reach the final answer. This feature is invaluable for enhancing your grasp of algebraic concepts.

3. Varied Functions

The best algebra calculators offer a wide range of functions, from solving linear equations to graphing functions. You can explore different algebraic concepts and tackle various problem types with a single tool.

4. Error Minimization

Algebra calculators significantly reduce the chances of calculation errors. By automating the process, they ensure accurate results, allowing you to focus on the conceptual aspects of algebra.

5. Learning Support

While algebra calculators provide quick solutions, they can also serve as learning aids. Many come with tutorials, explanations, and examples to help you build a deeper understanding of algebraic concepts.

Choosing the Best Algebra Calculator

When it comes to mastering algebra, choosing the right algebra calculator is crucial. Look for one that aligns with your specific needs, provides clear and user-friendly instructions, and offers a comprehensive set of algebraic functions. Additionally, ensure that it provides an intuitive interface and excellent customer support for any questions or concerns.

In Conclusion

Mastering algebra is not only essential for academic success but also a valuable skill for real-life problem-solving. The best algebra calculator can be your trusted companion in this journey, simplifying complex problems, enhancing your understanding of algebraic concepts, and ultimately helping you gain the confidence needed to excel in algebra and beyond. So, whether you're a student looking to improve your math skills or a professional seeking to apply algebraic principles, consider adding the best algebra calculator to your toolkit.

#myassignmenthelp #Algebra Calculator

0 notes

vidfom-com · 4 years ago

Text

Class 11 Maths Chapter 1 - English Medium

NCERT Solutions for Vidfom.com for Class 11 Maths Chapter 1 - English Medium includes all the important topics with detailed explanation that aims to help students to understand the concepts better. Students who are preparing for their Class 11 exams must go through NCERT Solutions for Vidfom.com for Class 11 Maths Chapter 1 - English Medium. Going through the solutions provided on this page will help you to know how to approach and [solve the problems.](https://www.vidfom.com)

Students can also find NCERT intext, exercises and back of chapter questions. Also working on Vidfom.com for Class 11 Maths Chapter 1 - English Medium NCERT Solutions will be most helpful to the students to solve their Homeworks and Assignments on time. Students can also download NCERT Solutions for Vidfom.com for Class 11 Maths Chapter 1 - English Medium PDF to access them even in offline mode.

NCERT Books for Class 11 Maths – English Medium

Chapter 1: [Sets](https://www.vidfom.com/2020/10/ncert-solutions-for-class-11-maths.html)

Chapter 2: [Relations and Functions](https://www.vidfom.com/2020/10/ncert-solutions-for-class-11-maths_3.html)

Chapter 3: [Trigonometric Functions](https://www.vidfom.com/2020/10/ncert-solutions-for-class-11-maths-chapter-4.html)

Chapter 4: [Principle of Mathematical Induction](https://www.vidfom.com/2020/10/ncert-solutions-for-class-11-maths-chapter-4_5.html)

Chapter 5: [Complex Numbers and Quadratic Equations](https://www.vidfom.com/2020/10/ncert-solutions-for-class-11-maths-chapter-5.html)

Chapter 6: [Linear Inequalities](https://www.vidfom.com/2020/10/Class-11-Maths-Chapter-6%20.html)

Chapter 7: [Permutations and Combinations](https://www.vidfom.com/2020/10/Class-11-Maths-Chapter-7-English-Medium.html)

Chapter 8: [Binomial Theorem](https://www.vidfom.com/2020/10/class-11-maths-chapter-8-binomial.html)

Chapter 9: [Sequences and Series](https://www.vidfom.com/2020/10/Class-11-Maths-Chapter-9-English-Medium.html)

Chapter 10: [Straight Lines](https://www.vidfom.com/2020/10/Class-11-Maths-Chapter-10-English-Medium.html)

Chapter 11: [Conic Sections](https://www.vidfom.com/2020/10/class-11-maths-chapter-11-conic.html)

Chapter 12: [Introduction to Three Dimensional Geometry](https://www.vidfom.com/2020/10/class-11-maths-chapter-12-introduction.html)

Chapter 13: [Limits and Derivatives](https://www.vidfom.com/2020/10/class-11-maths-chapter-13-limits-and.html)

Chapter 14: [Mathematical Reasoning](https://www.vidfom.com/2020/10/Class-11-Maths-Chapter-14-English-Medium.html)

Chapter 15: [Statistics](https://www.vidfom.com/2020/10/class-11-maths-chapter-15-statistics.html)

Chapter 16: [Probability](https://www.vidfom.com/2020/10/Class-11-Maths-Chapter-16-English-Medium.html)

Here we are providing the Chapter-wise NCERT Book for "Class 11 Maths Subject". Students can easily download and access the chapters of Class 11 Maths. Digital edition of "NCERT Books Class 11 Maths pdf" are always handy to use when you do not have access to a physical copy. Here you can get "Class 11 Maths" NCERT Books. The "NCERT for Class 11 Maths" Chapters wise relevant topic covered on this page.

NCERT Book for "Class 11 Maths" is a vital resource for students preparing for the 16th Class Examination. In this NCERT Books Class 11 Maths both books are provided with all chapters of the Civics Subject. Get here the complete chapters wise study material of "NCERT Book Class 11 Maths".

We suggest you go through NCERT Book for Vidfom.com for Class 11 Maths Chapter 1 - English Medium and get the distinguished study materials. Practising these study materials will help you a lot in your school exam & board exam. All NCERT Chapters for Vidfom.com for Class 11 Maths Chapter 1 - English Medium given here are as per the latest syllabus

Chapter 1 - English Mediumedium help you. If you have any query regarding Vidfom.com for Class 11 Maths Chapter 1 - English Medium drop a comment below and we will get back to you at the earliest.

#Class 11 Maths Chapter 1 #Class 11 Maths #Ncert Class 11 Maths

1 note · View note

designfordisplay · 6 years ago

Text

Marstine, J. (Ed) (2006). New museum theory and practice: An introduction. Malden, MA: Blackwell.

Notes:

Museums are so ubiquitous/omnipresent in our ‘“cultural landscape that they frame our most basic assumptions about the past and about ourselves”.

A lot of people’s perceptions of history are based of what is displayed in museums. This can be dangerous as it can manipulate and focus people’s mindsets, not allowing for alternate and contradicting histories - Hiroshima vs Enola Gay.

Huge controversy over who the items may belong to - a lot of Maori taonga was confiscated and taken and is not connected to its whakapapa. These such items on display have tikanga surrounding how it should be handled etc.. te papa enforced the mana taonga principle to ensure cultural significance and history are taken into consideration when dealing with taonga. Tribal elders are also asked for advice. Other places do not have respect for the items in their possession or do not care that they are reunited with their whakapapa - what ever culture they may be from. Such as the elgin marbles of greece who are in in the possession of the British Museum where they refuse to return them - stating that they were “rescued” and that the british are keeping them still to guard against damage from the neglect, earthquakes and pollution they might face in greece. Timothy webb says that they have come to represent britain as the “inheritor of democracy from ancient athens” and in turn, justifying their “political” decisions such as “colonisation and domination of other peoples”. Greece is seeing this as a humans rights issue- sculptures were gained through illicit means (stolen) and they are being denied of their heritage.

We see museum objects as ‘unmediated anchors to the past’ - teachers often take students to museums making real of the things talked about in class.

But they’re not authentic a lot of the time, museums are about individuals making subjective choices - mission statements, architecture, exhibition display etc.. what is meant to be a neutral space is influenced by ‘subconscious’ opinions.

What does it mean for something to be ‘authentic’? “Claiming authenticity is a way for museums to deny the imperialist and patriarchal structures that have informed their institutions. They control the viewing process and suggest a tightly woven narrative of progress, an ‘authentic’ mirror of history.

Andreas Huyssen believes that museums are a mass medium, “a hybrid space somewhere between public fair and department store”. ‘They are a response to the quest for authenticity fueled by the cultural amnesia of our times; the information overload and fast pace of the digital revolution evoke a desire for stability and timelessness.

Museums are well trusted, american association of museums survey, 87% deem museums trustworthy vs 67% books and %50 tv news.

New museum theory (critical museum theory/new museology) - while workers ‘naturalise’ their policies and procedures as professional practice, the decisions made reflect underlying value systems that are encoded in institutional narratives. Its about decolonising and giving those represented control of their own cultural heritage (mana taonga principle) real cross-cultural exchange. 1960s artists began to demand a voice in determining how their works were displayed, interpreted and conserved. The civil rights movement challenged the museum to be more inclusive.

What is a museum? These categories are not mutually exclusive and overlap.

Shrine: longest standing and most traditional view of the museum is as a sacred place. Has therapeutic properties, place of sanctuary removed from the outside world.collections are fetishised, objects ‘possess’ an aura that offers spiritual enlightenment. Leads people to assign meanings to objects unrelated to their original function. Objects are prioritised over ideas. Collections are thought to be reborn in museums, where they are better guarded and more appreciated. The shrine idea is influence by church, palace and ancient temple architecture - processional pathways, staircases, dramatic lighting.. Create and performative experience. ‘All museums stage their collected and preserved relics… (museums) use theatrical effects to enhance a belief in the historicity of the objects they collect.’ - Prezoisi.

market-driven industry: museums often position themselves as being ‘pure’ and unsullied by commercialisation. Obviously people understand the items are valuable but this information is usually hush hush - would commoditise the objects. Heritage and tourism are collaborative tourism. Museums have borrowed from the theme park and cinema to create a spectacle that engages all the senses.

colonising space: often look to/reference a postcolonial (eurocentric perspective) history. Appropriate objects from non-western cultures to tell their own history. Naturalise the category of ‘primitive’. Indigenous individuals were rarely acknowledged - seen as following conventions while ‘original’ western artists were seen as groundbreaking and intellectuals. Destroys rather than preserves. UNESCO declared that repatriation is a basic human right. Mansuline gaze

Post-museum: no longer a museum. Will acknowledge the politics of representation, actively seeks to share power with the communities it serves and the source communities. Encourages diverse groups to respond in museum discourse. Curator takes responsibility for representation. Doesn’t shy away from difficult issues but exposes conflict and contradictions. Redress social inequalities. Promote social understanding. Responsibility always rests with the researcher

Greater accountability, sensitivity and openness

Michel foulcault - epistemes -

Renaissance:15/16/17th century humanist desire to understand the world through seeking universal knowledge.science over theology. Finding relationships between objects, microcosm of god. Curiosity cabinet - mediates between the microcosm of humankind and the macrocosm of god and the universe. Precursor of the museum to represent the world in miniature - was private though

Classical: mid 18th century world was too complex, chaotic and fragmented to be contained in the cabinets. Linnean taxonomy classifies the natural world by genus and species. Repositories, study collections that were privated were founded for scholarly research. The rare in the laws of nature was rejected and seen as uncharacteristic or were made to fit in. displays were linear and embrace an ideology of progress.

modern: late 18th century marks the end of elitist institution and beginning of democracy. Military practice became standard. Biology and philosophy arose. Disciplinary public museum -accessible to all. Aimed to fashion modern citizens. Art was royal, aristocratic or ecclesiastical contexts and reclaimed national patrimony and democratise and secularise the viewer. Temporary exhibitions were formed to celebrate napoleon's birthday.

(can’t change) Many believe museums still conform to this modern model. They may create new spaces and exhibitions for consumptions but at heart, remain elitist institutions. The decision making process often refrains from scrutinising their own histories. Continue to attract (more art galleries) an educated upper and middle class audience, often times remaining irrelevant to marginalised groups. They aim to generate consensus rather than conveying differing perspectives. Curators are above education department. Quantitative vs qualitative.

Are museums able to change or are they becoming obsolete?

(can change) they can because deconstructing the traditional value systems in just the beginning. Can occupy a third space, beyond elitism and consumerism. Some curators are eager to share power by initiating open dialogue and forging new partnerships with groups previously disenfranchised. There are many organisations that are taking diverse approaches to the representation of race, ethnicity, class and gender. Time of the museum as a ‘great collector’ is past. Provenance is important to consider!! Finding culturally sensitive ways to treat non-western objects. Museum is more than a material collection - a lot are still stuck with this. FORUM.

Biggest change comes with the relationship between institution and audience - should be equal. Some are supporting educational research that theorised the museum experience. Acknowledging diverse learning, lectures, performances, videos, workshops etc…

Constitionaries

Visitors must be critical about the choices made by museums.

2 notes · View notes

edsbrak · 6 years ago

Text

let the light in

pairing: Steddie word count: 3k summary: Eddie wants to have his first kiss. Stan unexpectedly volunteers.

Read on Ao3 here!

(a short n sweet little steddie drabble bc I love them and I couldn’t stop thinking about this prompt for weeks! I hope you guys like it! enjoy! xx)

Being in the Kaspbrak household always keeps Stan on edge – mainly because of the woman downstairs he and their group of friends all call ‘The Terminator’. Not in front of Eddie though, of course. Stan knows that even with how crazy she is, Eddie would still take offence to it, his small stature figuratively growing in what Stan believes is just Eddie defending himself instead, not her.

It’s only himself here at the moment, perched precariously on Eddie’s desk chair as said owner of the chair sits comfortably on his bedsheets, legs crossed as he nibbles absentmindedly at the end of his pencil. Stan wants so badly to rip it out of there, watching as the thin layer of mental bends with each bite of Eddie’s teeth.

Eddie had asked him earlier that morning at school if Stan could come over and help him with an assignment. He’d agreed, knowing Eddie must really be struggling if he was asking just Stan.

They’d ditched the other Losers and watched as they made their way over to the Aladdin as he and Eddie turned the other way. These days Mrs. K only ever let Eddie have friends over if it was for study purposes, and they’d both shown their math textbooks as proof when they’d walked through the front door not an hour ago.

“How are you going with question five?” he asks after a few minutes of silence have passed. Stan himself finished up 10 minutes ago, but Eddie hasn’t written anything down in that time, which Stan guesses means he’s struggling again.

“Fine,” Eddie lies.

Eddie knows how Stan feels about lying, so he must really be determined to work this out by himself. But it would only defeat the purpose of inviting Stan over to help him in the first place, so slowly Stan gets up to walk over to the bed and sit down on the edge.

“Really?”

Eddie huffs quickly before shifting his book up further to his face. Stan sighs gently and reaches out to lower it.

“Where are you stuck?” he asks.

Eddie’s mouth twists, and that’s one thing about Eddie that is like Mrs. K: they’re both stubborn in nature.

“Here, let me show you…” Stan says tentatively, trying not to sound pitying, knowing Eddie hates it whenever anyone treats him incapable of doing things.

He begins going over the numbers, being cautious not to talk too fast. The Losers were all in junior year at the moment, and both he and Eddie were taking advanced mathematics. Eddie because Mrs. K had it out for the other maths teacher at school and demanded he be transferred, and Stan because his parents discovered how well he could calculate when he was 10 and in his dad’s study counting up the bills.

When he’s done, Eddie mumbles out a small ‘thank you’ before he tries his hand at it. Stan watches on, shifting sideways on the bed so his back isn’t twisting uncomfortably anymore. Eddie’s nose scrunches up as he works, the end of his tongue peeking out occasionally as he writes down each equation. It’s endearing enough that Stan becomes distracted and misses the moment Eddie finishes writing the answer and he’s looking at Stan with a proud smile, eyes deep and wide.

Stan clears his throat before reading over Eddie’s reasoning, finding that it all checks out.

“Nice job,” Stan smiles back. “Pretty soon you’ll be making linear inequalities your bitch.”

Eddie fake gasps. “He swore.”

“Don’t tell anyone I’m funny either, or else I’ll have to kill you,” Stan whispers dangerously, and it only puts Eddie in a state of giggles. Stan finds he enjoys it very much.

They work on finishing up the next 4 questions together, each one longer than the last, their shoulders touching as they lean up against the wall. Eddie thinks if he can get them done quickly they can still meet up with the other Losers and maybe head down to the quarry and soak up the remaining hours of daylight. In a perfect world it might be possible, but Stan isn’t sure about Mrs. K letting their little club interrupt her son’s precious dinnertime.

By question 8 Stan gets up to use the toilet, going through the process of washing his hands three times before closing the door behind him. As he’s walking back, Eddie appears stuck again, looking anywhere but his textbook as he chews on his bottom lip.

“Everything okay?”

Eddie’s eyes snap up to meet his, and he looks away just as quickly. Stan frowns, wondering what could have happened in the time he was in the bathroom.

“Nothing, ‘s fine,” Eddie mutters.

“Clearly,” Stan challenges.

Neither say anything else for a beat, until Eddie’s shoulders unclench and he releases a deep sigh. He looks slightly uncomfortable and Stan can’t help but be a little on edge about it.

Finally, Eddie says, “Have you had your first kiss yet?”

Stan blinks, not expecting that to be the cause of Eddie’s stress. “What?”

“I feel like I’m the last one in the group to have a first kiss,” Eddie continues as if Stan hadn’t said anything. He’s twisting his pencil around, obviously nervous. “We know Bev, Bill and Richie have all kissed someone, right?”

Stan sighs softly. He sits down again where he’d been before, thinking over his next words carefully. “Well, I can’t say for sure about everyone. But…” he stops to swallow. “No, I haven’t had my first kiss yet.”

Eddie doesn’t react with surprise like Stan had thought he might. He’s still biting his lip as he looks at something across the room, as if deep in thought. Stan is about ready to move on with this conversation and return Eddie’s focus to his homework, but Eddie isn’t finished with it yet, apparently.

“Stan, I…” he starts, gaze darting every which way before he shakes his head. “Um, never mind.”

There’s a feeling deep in Stan’s gut, an inkling to what might have been on the tip of Eddie’s tongue. It sends a shiver up his spine; unexpected, but not unwelcome. Mind working a mile a minute, he goes through all the ways in which this could be damaging territory; instincts yelling at him to let it go. But there is a small part of him, hidden deeper; a part he isn’t sure he was even aware of until right now, as if Eddie had unlocked it with his perfectly innocent question.

Breathing through his nose, Stan exhales with a tremble before uttering, “We can try it.”

Stan’s suspicions are confirmed when Eddie’s expression morphs into surprise.

“We can kiss.” Stan isn’t sure why he repeats his statement. To assure Eddie or himself, he doesn’t know. “That’s… would you like to?”

Almost in slow motion, Eddie nods in answer. His eyes are still blown wide, like he’s waiting for Stan to yell ‘Ha! As if I’d kiss you, weirdo!’ To show he’s serious, Stan removes the textbooks in Eddie’s lap and places them carefully off to the side out of harm’s way. Eddie is still frozen, and Stan stops to ask, “Eddie?”

Instantly he’s snapping out of it, but still looking unsure. “Right. Yep. Okay.”

“We don’t have to,” Stan offers gently.

Eddie is shaking his head again before Stan even finished. “No, I want to.” And he sounds genuine this time, eyes set as he glances down to Stan’s lips occasionally. “I trust you.”

Stan feels another thrill, trying to keep it under wraps because it seems like he’ll be taking the reins on this one, despite the both of them being unfamiliar in this area. The most Stan has ever seen of kissing is from his parents and the various movies they all watch together. Eddie on the other hand, Stan thinks, is less aware, only having Richie’s less than tact descriptions about him and some girl going at it behind the school’s sports shed.

“Okay, well…” Stan stops to think again. “Let’s get comfortable first, right?”

“R-right,” Eddie answers, but when he makes no move Stan takes initiative and scoots back to the edge of the bed, feet planted on the ground. Eddie follows, his hand brushing against Stan’s as he goes. “Now what?”

“I guess we just… kiss?” At Eddie’s small noise that directly translates to ‘And?’, Stan clears his throat. “Alright. Well, when kissing, you close your eyes just before your lips touch.”

“Right,” Eddie nods, licking his lips almost subconsciously.

“And it’s best of your lips aren’t too wet, either,” Stan adds, hating when his aunts greet him at family gatherings with a spit-slick kiss on his cheek. Immediately Eddie is wiping at his lips with the back of his hand and Stan inwardly smiles. “Okay, we’ll start with a small kiss first; closed mouth.”

Eddie releases a slow breath, hands fisted into the sheets by his sides. Stan keeps one hand in his lap and the other on the bed next to Eddie to maintain some balance. Tentatively, he leans in, eyelids dropping halfway as he watches Eddie copy his movements. There’s no denying how badly Stan’s body is shaking right now, not wanting to screw this up as he puts on a front of faux confidence.

When their noses brush his skin tingles, and this close up, Stan can see Eddie’s freckles ever clearer than usual. Before he can chicken out, Stan closes the remaining gap and blindly finds Eddie’s lips in a soft kiss.

It lasts maybe 3 seconds, but for Stan, at least, it felt like a lifetime. A good one at that.

Simple, quick, foolproof.

They both draw back, and Eddie still has his eyes closed when Stan opens his.

“Was that okay?”

Eddie’s eventually flutter open, and Stan notices his cheeks are slightly flushed, eyes practically sparkling. “Yes.”

That one simple word is enough to have Stan boasting on the inside, completely chuffed he was able to give Eddie a nice first kiss after all. Feeling accomplished, he pulls back further to give Eddie his space, only Eddie doesn’t look relieved that it’s over, more like he’s shocked that Stan is moving away at all.

“Wait,” he says, his hand landing on Stan’s forearm quickly.

Stan gives him a curious look, trying not to linger on the heat emitting from Eddie’s skin. “What is it?” Perhaps he read the signs wrong and Eddie actually isn’t satisfied with that being his first kiss experience.

“Do you think…” Eddie’s hand grips tighter, almost fidgeting. “Can we… do it again?”

“You… want to do it again?” Stan repeats, more so making sure for his own sake.

“I mean, we don’t have to—” Eddie murmurs, withdrawing.

“No!” Stan interjects, lowering his voice when Eddie jumps slightly. “I mean – yes, I – I would like to.”

Eddie almost appears to sag in relief, energy giddy if Stan had to describe it somehow. They resume their previous positions, this time slightly closer than before.

“I know people begin to move their lips when they get more confident, right?” Eddie asks.

“Yeah,” Stan says. Despite having just kissed each other, the thought of kissing Eddie again suddenly has Stan even more nervous than before. “Keep it slow and steady. Remember to breathe through your nose while you do it.”

“Okay.”

Stan’s pulse quickens when Eddie grabs onto his arm again, shifting in as close as they can possibly be while sitting side by side. They begin to lean in, eyes slipping shut when their lips are close enough, and it’s just as electric as before when they press together.

Stan tilts his head marginally, his free hand twitching with a need to grasp something. And then Eddie opens his mouth slightly and Stan follows suit, lips parting as his bottom lip slips in between Eddie’s own naturally. He can feel Eddie’s breath hitch, obviously forgetting to breath with his nose, but Stan can’t bring it in himself to stop and remind him, so incredibly overcome with glee as he slowly becomes lightheaded from the feeling of… everything.

He can hear the small wet sound when their lips separate, slow and intimate, and without realising what he’s doing, Stan reaches up to cup Eddie’s cheek to angle Eddie to his other side. Stan reconnects their mouths again, working in tandem as he guides Eddie through the motions of it. Stan can’t believe they’ve managed to get this far, and from the sounds of it, Eddie is pleased with the results.

Eddie makes another small noise, a happy one, Stan’s sure, and Eddie’s other hand moves up so he’s gripping both of Stan’s arms tightly, like he’s scared he might fall.

Only when an unexpected touch appears in the form of the tip of Eddie’s tongue does Stan draw back, slightly startled as he looks at Eddie questioningly. Eddie seems embarrassed until he starts to panic at Stan’s expression.

“Sorry, I’m—” he says through short puffs. “I didn’t know if – I – I thought that was the next step. At least, that’s what Bill and Richie say—”

At the mention of their friends names, Stan can’t help but fixate on it. The entire Losers club, sans Bill, are all aware of Eddie’s childhood crush on their unofficial group leader. Stan’s never stopped to ask Eddie if he still likes Bill, and now he’s wondering why that’s even something to worry about at all. But the thought of Eddie kissing someone else after this, of maybe just using Stan as a means to show Bill that he’s more mature and grown up now doesn’t sit right with Stan.

Mind clouded with Eddie and Eddie only, Stan shocks himself and reacts purely on impulse as he dives back in to claim Eddie’s lips. He ends up hitting the corner of Eddie’s mouth, and there’s a small struggle as they rearrange for a better fit, lips moving more urgently than they need to be as a wave of need and want washes over Stan unexpectantly.

Eddie releases his grips on Stan’s arms to grab the collar of his shirt instead, pulling him in impossibly closer as Stan cups both sides of Eddie’s face.

Lips detach and reattach, sharing breaths and teeth accidently bumping together. Feeling bold, Stan tries what Eddie had done and pokes his tongue out, slowly grazing over what he thinks is Eddie’s top lip. Eddie produces a noise that makes Stan’s blood pulse, buzzing all around him. Finally their tongues both touch, not delving deep but sliding together occasionally as Eddie’s hands roam up closer to Stan’s hair.

Stan doesn’t know how it got to this point and isn’t sure he cares. “Eddie,” he manages to whisper between their mouths, and Eddie takes this as a sign to draw his feet off the floor and twist, desperate to keep their lips connected as he moves.

Stan isn’t sure where he’s going until Eddie is trying to get one leg over Stan’s to land in the middle. Instinctively Stan allows it, nerves overwhelmed as Eddie towers over him and sucks all of the air out of his lungs, fingers pin-points of warmth along his skin.

It’s nothing like Stan thought it would be and everything he’s glad it is.

Just when Stan’s sure his heart is about to jackhammer right out of his chest, a shrill cry booms from downstairs.

“Eddie! Dinner!”

They practically jump apart as if they’ve been burned, Eddie stumbling back on the carpet as Stan stays locked on the bed. They’re both panting hard, faces flushed and lips shiny with spit. When Eddie makes no effort to answer his mother, she predictably calls up again.

“Eddie-bear!”

Eddie visibly swallows. Stan is thankful Mrs. K never wants to trek the short walk up the stairs, otherwise she might have caught them in the act, and there is no way that could ever end well.

“Coming, ma!” Eddie manages to get out.

As if his ass is suddenly on fire, Stan shoots up from the bed and begins to pack up his things at the same time he tries to calm his body down.

“I’ll, um…” he begins, zipping his bag all the way over and hiking it over his shoulders. “I should go.”

“Right,” Eddie says, voice small.

Neither make a move for a few seconds, just staring at each other like their brains were just now finally catching up on everything that just transpired. It honestly felt like a fever dream, like stepping out of the twilight zone and back into reality after years without it. Stan can’t believe his first ever kiss was with Eddie of all people, and even more surprising he can’t think of one single fault in that knowledge now. It just feels right.

Clutching his backpack straps, Stan nods and begins the walk downstairs with Eddie in tow. Mrs. K is in the lounge room, dinner set up on the small table next to her, and she looks over at the two boys when they pass.

“Did you get your homework done, Eddie?” she asks.

“Yes, mommy,” Eddie mumbles.

“Good boy.”

There’s a lot Stan wishes he could say but knows he can’t. Instead, he says his goodbyes to Eddie before reaching for the doorknob, heart still beating fast even when he steps outside into the fresh air. He takes a moment to compose himself, straightening out his collar and hair as he sucks in several deep breaths.

As he starts to walk away, the shocking revelation in the pit of his stomach only seems to grow, desperate to find out exactly what was going to happen now that he and Eddie shared a moment together that Stan would argue was anything but a friendly lesson of kiss-and-tell. And before he can fester anymore on it, he hears the familiar creek of the front door opening and small, fast steps running after him.

“Stan!”

Stan turns around, about to ask Eddie what could be wrong, but his words are silenced when Eddie leans up to kiss him swiftly.

“Oh,” Stan says when it’s over, unable to think of anything else.

Eddie is already stepping away, expression shocked like he’s surprised by his actions, and he leaves Stan with these parting words: “See you tomorrow in class?”

Stan simply nods, watching as Eddie disappears back up into his house.

Maybe it’s not the exact answer his fast-working mind wants right now, but in his heart, he knows it’s the best one he could have gotten.

Stan smiles all the way home.

#steddie #my fics #pure fluff honestly #spread the love!!

80 notes · View notes

helpmyassignment028 · 2 years ago

Text

Math Assignment is one of the most popular online tutoring companies which helps students from small schools to high schools with their mathematics assignments. The professional writers are hired from the U.S. and they have years of knowledge in mathematics assignment, having studied at a math major university or have had experience teaching math at the high school or college level. Expert writers can write any type of assignment which includes: Algebra: equations, inequalities, graphs, and other types of algebraic expressions; matrices; linear combinations, sequences, and series; quadratic functions and their equations; trigonometry formulas, triangles on the coordinate plane ( including Pythagorean theorem and the law of sines); factoring polynomials; matrices; permutations and combinations.

#psychology assignment #Social Science Assignment Help #do my biology homework #Math Assignment help #Law Assignment Help online #dbms practical assignment #Java Assignment Helper #c++ homework help #writing help online #Cheap Assignment Writing #assignment help #finance assignment helper #writing assignments #assignment example #social science assignment #cheap assignment writing service

0 notes

praadiseducation · 3 years ago

Photo

NCERT Solutions For Maths Class 7 section discusses the basics of solving problems in class 7 maths. The objective of this Class 7 Maths NCERT Solutions is to learn how to solve problems in Class 7 Maths, including linear equations, quadratic equations, inequalities and simple arithmetic. This section is about the Maths NCERT Solutions for Class 7. NCERT Solutions For Class 7 Maths are designed to help you in preparing for your exams. NCERT Solutions Maths for Class 7 are also designed to help you with your homework and assignments.

#NCERT Solutions Maths for Class 7 #NCERT Solutions For Class 7 Maths #Maths NCERT Solutions for Class 7 #NCERT Solutions For Maths Class 7 #Class 7 Maths NCERT Solutions

0 notes

acemywriter · 3 years ago

Text

Week 9 work

I need someone to complete my week 9 homework. You will need to certify in the problems. Make sure that you have completed the Unit 9 Preparation and Overview. Complete the following assignments for Unit 9, either by clicking the Hawkes Learning tool on the homepage, or the assignment links below:Inverses of Matrices Linear Inequalities in Two Variables Linear Programming Nonlinear Systems of…

View On WordPress

#Writing

0 notes

jorlaudanrino-bct · 6 years ago

Text

Reflective Journaling: Low Fidelity Models of Data (Week 1)

Looking back at the past week, I saw just how difficult and challenging it was for me. Usually, I’d locate and research a particular data set before I’d go about making multiple models. The activity to create multiple low fidelity models was hard for me to do. I often found myself resorting to very linear and graph-like models because I didn’t have very many ideas. However, from what I did, I found that I wanted to focus more on statistics on domestic violence and abuse. I personally didn't feel any emotional investment in statistics about New Zealand’s trash and waste and feel like conversations start easier if the topic is something that puts people out of their comfort zones and makes them think and reflect.

This week was incredibly frustrating for me as it seemed like I wasn’t going anywhere with both finding data sets or creating models. However, after a quick sort of catch up or debrief lecture with Ricardo, I was able to see that despite my frustrations, creating these models taught me a lot about what kind of data I wanted to present and how I wanted to model various datasets.

Initial Data Set

The data I have chosen to focus on for now is the statistics for New Zealand’s domestic violence “It’s not OK” campaign. The statistics that stuck out to me particularly are the following;

76% of all domestic violence incidents in New Zealand are unreported

24% of women and 6% of men report having to experience sexual abuse in their lifetimes

20% of girls and 9% of boys have reported unwanted sexual touching or being forced to carry out sexual acts

Alongside this topic, I also had an interest in possibly presenting data about New Zealand and it’s waste, a topic I had covered in previous projects and assignment Semester One.

Popsicle sticks & pins around a centre point

This model was probably the most simple models that showed the statistics very obviously. However, this model didn’t really evoke any emotion which didn’t urge conversation. It seemed too simple and straightforward which meant nobody had to put thought into what it represented. The materials used (wooden popsicle sticks and a pin) also do not represent or have any relation to the subject of the statistics. What interested me about this model was its ability to move and the fact that while it was mostly linear, it also had a circular aspect to it.

Popsicle sticks, pins & yarn in a triangle

This model presents the data of only 24% of domestic violence incidents being reported to the police while 76% isn’t. The number of times the string is wrapped around the pins represent the rough/rounded percentages of this statistic. It was inspired by some string art I had previously come across, as shown above.

I sort of liked the way the model turned out because the thickness of the yarn made it difficult to count the exact number of times it had been wrapped around the pin meaning that you had to analyse the sort of thickness of the mass on each side to see the statistics. However, like the previous model, the materials or actual shape and make of the model have no relevance to the actual topic the data is showing. It also doesn’t really spark any conversation or make people think.

Woven yarn bracelets

To show the statistic of 20% of girls and 9% of boys have reported unwanted sexual touching or being forced to carry out sexual acts, I cut pink and blue yarn to lengths that represented the respective percentages and proceeded to try to braid a bracelet out of it. I wanted to see how the final product would look with different lengths.

By the time I had finished with this model, I feel that the data set I had did not work with this type of model. It made it feel as if I was comparing which group/gender had it worse which was not the intended purpose of my model. I wanted it to show just how many kids reported unwanted sexual touching. However, I think that this model would be good to show some sort of inequality. Looking back, I can also see that the bracelet, the final product, can represent childhood and children as jewellery and wearable items are often popular amongst children (eg. Scoobies, Loom bands etc.). By the final model being a wearable item, an individual has to opportunity to start a conversation wherever they go.

References

http://areyouok.org.nz/family-violence/statistics/

#CTEC503 #TangibleDataConversations

1 note · View note

ask-de-writer · 5 years ago

Text

This WIP is not MLP related at all. THE FALL OF OAKENFIELD UNIVERSITY is a Prequel to Slave in Pard.

This story is rated YA

THE FALL OF OAKENFIELD UNIVERSITY

De Writer (Glen Ten-Eyck)

6101 words so far, work is incomplete

Writing begun 06/03/17

Copyright fair use rules for Tumblr users Users of Tumblr.com are specifically granted the following rights. They may reblog the story provided that all author and copyright information remains intact. They may use the characters or original characters in my settings for fan fiction, fan art works, cosplay, or fan musical compositions. All sorts of fan art, cosplay, music or fiction is actively encouraged.

///////////////////////

Sande was humming happily to herself as she worked to clean Professor Standar's office. She was mulling over his recent lecture on the pervasive nature of the magical field that only unicorns, with their horns, could control. As she worked, she looked at the big office slateboard.

She was emptying his trash into a rolling bin. She added the dust that she had collected from his shelves, books and corners by the use of magic from her horn. To help her concentrate on the carpet, where her magic was making the dust rise and scooting it into the bin, she actually looked at what Professor Standar had chalked on his board.

A bit excited by what she saw, she took a chalk and went to the empty board. She wrote neatly, “Professor, I am 3rd year student Sande. I saw your problem because I am working part time as a janitor, and was assigned to clean your office.

“I believe that the problem that you are working on will reduce more easily as a five function matrix, like so.”

Under that, she chalked his beginning mathemagic and then the steps to convert the unwieldy original expression into a matrix. Then she proceeded to transform the matrix by clear steps to a solution.

She replaced the chalk in its tray and was turning to go when she found her way blocked by the Professor himself.

Mildly he observed, “I see that you have seen fit to use my chalk board. What did you think so important that you did not clean it off when you were done?”

He ambled over and began to examine Sande's derivation and solution carefully. Turning to her he spoke with mock severity, “This solves a problem that I have been working on for three weeks! That causes me a great difficulty. I now have to completely rewrite the opening of my latest paper to be presented to the Society. I have to include you as the one who provided the complete Mathemagical proof of the whole idea!”

He broke into a grin and gave Sande a hug. Leading Sande by the hand, Professor Standar practically skipped as he lead her away from her work cleaning his office.

As she was pulled along to the next building, her dark brown mane flipping about in the breeze, she panted, “Where are we going?”

Gleefully, Professor Standar replied, “To see Professor Greenleaf! He and I have been working on this paper for weeks but could not figure out how to derive the matrix from the essential expression!”

As they were entering the cool halls of the Mathemagical Annex, Sande puffed, “I do not think that this is a good idea. Professor Greenleaf does not like me.”

Professor Standar paused just short of knocking on an office door. He turned to Sande and asked, “Why would he not like you?”

She bit her lip nervously before replying, “I was sitting in on his Theoretical Mathemagic 620 symposium. He put up the assumption that only the horn of a unicorn could tap, shape and utilize the overall Magical Field. I questioned whether other things might be able to tap or alter the Field, since it is easily detected to be stronger near groves of trees, for instance.

“He grew very angry and angrier still, when he found that I was not even enrolled in that upper division class. After that, he has tried to get me removed from the University several times.

“He found that I have no Herd Backing nor support. I pointed out that the Greenswale Herd, that I came from, was merged with the Know Nothing Herd by force. He got all my scholarships pulled. I earned enough off of one job last summer to pay for my entire third year, books and lab fees included.

“He got my other work study jobs pulled, except for this janitorial one. That freed me enough time to entertain at foal parties and play table-top strategic games. Both pay quite well. The parties I do for fees and I place bets on the games.”

In a dry voice, Professor Standar asked, “Is that all? It seems more than a little extreme.”

Quietly Sande replied, “No. At the Mathemagic 302 mid term, he gave me a separate test from the rest. Nine problems on deriving and processing matrices and one on reducing raw data from a Metastable Structure experiment. He gave only three sheets to show my work.

“Without actually grading it, he simply wrote an F on it when I handed it in. I filed a departmental appeal. Three witnesses, two of them faculty, saw him do it.

“All that I asked for in the appeal was sufficient sheets to actually show my work in detail while the appeal committee watched and to be fairly graded on what I did.”

Professor Standar, nodded slowly, “I did not know that was you. I and the whole rest of the faculty heard about it. You needed fifteen sheets to show your work. At grading, YOU had to lead the Mathemagic faculty through your methods and reasoning. They gave you an A+.

“Since Mathemagic 302 only deals with Linear Expressions, both inequalities and equalities, the Appeal Committee removed you from the class with a stipulated A+ grade and pulled you from classwork entirely.

Professor Greenleaf was furious because the rest of the department gave you a challenge degree in Mathemagic.

“What are you working on now?”

Sande straightened up proudly, “I have been expanding Horimizu's zero sum placeholder expression idea. It is really quite interesting.”

Just at that moment, the door opened and the red roan unicorn looking out, snapped, “I heard that! Why are you even here? You have been forbidden to do janitorial work in the Mathemagic building!”

Professor Standar cut in, “I brought her here because she wrote something on my slate work board that . . .”

Triumphantly, Greenleaf interrupted, “She did? Excellent! I will have her cast from the University for this affront to Faculty!”

Professor Standar said mildly, “I said nothing about an affront to Faculty. In fact, I will give you the same twenty minutes that she had in my office to duplicate what she wrote. If you cannot, I will have you withdrawn from our Active Metastable Structures paper. What she wrote took our lab derived expression, which is on your work board too, and derived a matrix, processed it to a specific solution and from it derived a general solution.

“That is what I brought her here to show you.

“I see that you still are attempting to remove her from the University because she embarrassed you. Your efforts are a Direct Violation of the University's Primary Code.”

In outrage, Professor Greenleaf demanded, “How can you even say that! I have devoted my life to the development of Mathemagic!”

Sande stood back to let the Professors squabble it out.

Standar snapped back, “And at the first serious question of the basic assumption that our horns are unique in their ability to tap and manipulate the Magic Field, instead of investigating, as LOVE OF TRUTH would require, YOU tried to silence the questioner! Some LOVE OF TRUTH!

“That test that you gave to her, as a MIDTERM in Mathemagic 302? It was rated BY YOUR DEPARTMENT as a graduate level written and oral exam! She got an A+ and was removed from Mathemagical classes with both a Bachelors and a Master's Degree!

“Last year you conspired to remove her grants and scholarships to force her to leave! Instead, she did ONE job, over the harvest break and Paid THE FULL BALANCE of her third year in advance.”

Grimly, he demanded, “Twenty minutes, Greenleaf! The matrix, processing, specific solution, and general expression. That is all the time that Sande had and she did it!

“Match her work or lose the paper.”

Sande spoke up, concern in her voice, “No, Professor Standar. That would be a mistake. Simply because I did this part, does not mean that Professor Greenleaf would not have valuable input.

“In the Library I have read everything that he has published. Aside from the single error about the unicorn's horn being the sole means of harnessing and utilizing the Magical Field, his work is excellent.”

Sour at having his part in an important academic paper saved by a mare that he detested, Professor Greenleaf invited, “Why don't you come in and show me what she has stumbled onto?

“As for her mad assertion about the magical field being manipulated by anything but the horn of a unicorn, I have never seen any proof of it!”

Sande remarked casually, “After we have dealt with this expression, I will give you a free demonstration of a non horn initiated magical field accumulation.”

Gesturing at an empty slate board, she said, “With your permission?”

Growling under his breath, Professor Greenleaf snarled, “Go ahead! Show me what we have been missing!”

Nodding, Sande rewrote the basic expression with one more factor and began to reduce it into the matrix.

Greenleaf slapped the chalk from Sande's hand, pronouncing triumphantly, “This is garbage! The expression that you added works out to ZERO! It makes no difference!”

Sande gave him a withering glare and snapped, “Didn't the reprimand for PREGRADING my midterm in Mathemagic 302 teach you ANYTHING?

“In the SPECIAL CASE of THIS METASTABLE STATE, it is ZERO ONLY AFTER metastability is achieved. That is when all the measurements were made. That's why it was missed.” She turned back to the board and chose another piece of chalk to finish creating the matrix.

As she was processing the matrix, Professor Greenleaf's keenly watching eyes flew open! He grabbed a piece of chalk of his own!

Checking against Sande's matrix and her restatement of the original expression, he began to sketch a graph of his own. It started at zero and rose in an asymptotic curve to positive three, dropped to negative three and rose following a similar curve up to zero, where it repeated itself.

He then wrote out the solution to Sande's matrix and produced the generalized expression. He put his chalk down before Sande did and pronounced, “I not only beat her time, Standar, I have discovered a repeating function in the magical field that will be worth an entire paper by itself!”

Without pausing her work, Sande pointed to Greenleaf's chalk board and stated, “In ANY mathemagic class, that would be marked as a failure.

“You failed to show any of your work. Not the derivation of the graph points, not the matrix processing, nor the three steps from the specific solution to the generalized one.

“Besides, since I did get a departmentally given advanced degree out of your improperly administered and graded Mathemagic 302 midterm, I have the right to submit papers for peer review. MY paper covering that function and the other five revealed in examining data from other Metastability experiments is already in peer review.

“If you published that, when a faculty witness saw you lifting it out of my demonstration work, I would be forced to charge you with plagiarism.”

She put down her chalk and turned to Professor Standar and pointed out, “I did say that it would be a mistake to remove him from your paper. As you can see from what he has done here, as soon as he had a prompt in the correct direction, he is both brilliant and insightful in Mathemagical analysis.

“It is a pity that he has had to be given a formal Board of Deans Order of Non Interference about having any further contact with me academically or financially. That is why he is being kept from my papers until they are released.”

Reaching across Greenleaf's desk, Sande picked up a sheet of paper and a quill. Her eyes widened just a little. She glanced away from the desk top and began to draw a small design near one corner of the paper.

“This part is a trigger for the demonstration that I promised you, Professor Greenleaf. The rest of the design will be the Accumulator for the Magical Field, with no horn needed to create it or use it. She finished her drawing, bending the corners of the paper up over the design, Sande tore a small rip through the trigger part.

She sailed the folded paper toward the center of the room. With a green flash of released magical field, a loud and surprising POP! the paper suddenly burst apart into a fountain of small confetti! Only tiny fragments of shredded paper drifted to the floor.

While the others were both staring at the surprising result of Sande's demonstration, she snatched two bundles of papers from Geenleaf's desk and put them into her large waist pouch.

She calmly steered Standar out of Greenleaf's office while he was espostulating, “You promised to give me that demonstration! I must have a sheet with the design on it! You promised!”

Over her shoulder, Sande retorted, “I promised a demonstration of Magical Field Accumulation without the use of a horn! Not to show you how it was done! You got to see it happen! Now you know that it can happen! Your axiom about the unicorn's horn is PROVED wrong!”

Outside, Sande dragged Professor Standar to the office of the Dean of Schools of the University. Inside, she greeted the mare at the desk with, “Hi, Vanara! Do you have a file copy of the Greenleaf Academic Restriction notice with his signature? I need it and I need to see the Dean as soon as possible!” She slapped a short pile of paper on the counter.

Vanara turned to a file cabinet and extracted the document before saying, “What is happening, Sande? Oh! I see that you have the printing office galley proofs for your latest paper! Have you finished the markup yet?”

Grimly, Sande replied, “I did not get them from the printing office. They were intercepted and being improperly marked up by Professor Greenleaf. Along with the markup, he was writing a rebuttal, part of which claims my expansion of Horimizu's zero sum placeholder expression. I have it, too.”

Vanara reached across the counter and took the galley proofs to examine. She held out a hand for the rebuttal paper and examined it.

She signaled one of the waiting student office runners.

Grim of voice, Vanara instructed, “Get the Printing Office sign out log for . . .” she examined the galley proof and finished, “Junnea fourth, this year. Bring it directly to the office of Dean of Schools Honner.”

The runner simply repeated, “Galley sign out log for Junnea fourth, Dean Honner's office, yes Mam!” He left at once.

Vanara left her desk and went to a door down the hallway that her counter blocked access to. There was a swift but quiet conversation. Vanara gestured for both of them to come to the office.

As they were seating themselves, Sande noticed the headline of a newspaper hanging over the desk of Dean Honner. It proclaimed, “Know Nothing Herd Burns Leafhome University!”

She commented to Professor Standar, “See that? It means that we are the last college or university left between the Southern Sea and the Skywall Mountains.”

Standar replied, “I know. The Know Nothings tried to use their 'common sense' thinking to guide farming in the nation of South Plains. It has resulted in a massive crop failure and much spoilage of what was harvested. Grains of all sorts were especially hard hit.”

Sande whistled softly. “They were only just recovering from that drought. This crop failure will cause a flood of refugees from that whole area. Where will they go?”

Dean Honner shrugged, “Disaffected unicorn refugees have been making their way through the only known pass in the Skywall for over twenty years, now. There is supposed to be a rich plain on the other side, called the Green Sea. I expect that many of them will go there.”

Sande pointed out, “Perhaps not all that many. If reports are to be believed, that Green Sea colony has been at war for nearly five years with a confederation of tigers and leopards called Pard. Even if I was hungry, I am not sure that I would want to go to some place where I might get eaten!”

Dean Honner nodded. “I do understand what you are saying, Sande. Unfortunately, that is not all the story. The Green Sea colony is also sending several tonnes a month of top quality fodders back through the pass.”

Sande quietly touched her lips before saying, “Suddenly I can see the motivation for starving herds to take that risk.”

Vanara re entered the room and placed a folder on Dean Honner's desk. As she was leaving, Professor Greenleaf barged into the room, pushing her out of his way!

Ignoring all else, Greenleaf planted both hands on Dean Honner's desk and demanded, “You must dismiss that MARE, Sande, at once! She entered my office, where she has no right at all, and she STOLE important papers from my desk!”

Professor Standar interrupted Greenleaf's tirade dryly with, “Actually, Professor, that is WHY we are having this meeting with Dean Honner. It appears that . . .”

Greenleaf rounded on Standar, in the process seeing Sande for the first time. “What is that MARE doing here? She stole papers from my desk! She was not even supposed to be in the Mathemagic Building at all!”

Professor Standar pointed out calmly, “She is filing a formal complaint against you, Professor Greenleaf. The charges are violation of the University's restriction on contact with Sande or pre-publication access to her papers or other intellectual works or property.

“Speaking of theft, you took the galley proofs of her paper expanding Horimizu's zero sum placeholder expression. You were re writing it to make it appear to be intellectual garbage while claiming her insights and discovery as your own in a 'rebuttal' paper.”

“I would never stoop so low! She is a mere mare and a only a third year student, besides! As such, she has no right to lofty thought! As a student, she cannot properly publish papers in any case!”

Dean Honner interrupted dryly, “Greenleaf! The reason that THIS third year student CAN publish papers is those Bachelors and Masters degrees that she won from fair judging of her midterm exam given by YOU, last term.

“The brilliant work on those fifteen pages of Mathemagic that she needed to answer your nine questions, two of which were classical unsolved conjectures, BECAME her first paper, and YOU KNOW IT! Since then, she has already published two more papers and had the final peer reviews done and galley proofs prepared for her FOURTH paper, the one that you directly stole from the Printing Office.”

Dean Honner flipped open the file that Vanara had given him. Greenleaf blanched as he recognized the contents of the file. It was the Printing Office's Sign Out Log for Junea Fourth and under it were several standard Witness to Conflict forms.

Spreading out the incriminating evidence, Dean Honner continued, “Your inability to recognize her obvious intellectual capacity AND your continued efforts to have her removed from the University alone would have caused what I am now forced to do. Add to those infractions, your direct violation of the Board of Deans order of Non Interference by this outrageous attempt to plagiarize her work and discredit her, force me to enforce the Non Interference Order's penalty clause.

“Professor Greenleaf, your tenure at Oakenfield University is terminated! One more infraction and you will be removed from the faculty. Am I clear?”

Dean Honner gave Professor Greenleaf a red sheet of warning. He added, “After this egregious violation of the University's trust, you may not even publish comments or letters regarding ANY of Sande's work.

“Please leave my office. If I have to call you back, it will be to sever you from the University.”

The furious Greenleaf slammed the door on his way out.

Dean Honner shook his head at Greenleaf's behavior. Then his distinguished white furred muzzle broke into a smile and he asked, “Sande, are you going to be at the Horn and Hog for War Game Night tonight?”

She nodded, her horn bobbing happily as she replied, “I am looking forward to it, Sir. You give me a real challenge.”

Standar looked up at the framed medals and Wide Plains general rank badges on Honner's wall and said skeptically, “How often can you win against a general of Honner's experience?”

It was Honner who suggested, “Why not come and see for yourself? If I am lucky, I win two out of five games with her. Sande really keeps me sharp.”

That afternoon, Professor Standar accompanied Sande down the well shaded cobbled road to the village of Oaken Woods. The many farms surrounding Oaken Woods showed clearly the beneficial effect of being close to the famous University. The fields and orchards were not only well tended, they were filled with the unique and highly productive strains of fruits and grain provided by the Agricultural School. To his pleasant surprise, he saw the farmers using metastable structures in the harvesting of hay and grain.

As the muscular field mares swung their scythes to fell the crops, the metastable structures attached to the scythes gathered it into shocks and bound it with strings of twisted grass stalks. On the farms, even the stallions were working to get the crops into the barns. They were pulling big farm wagons that were being loaded by stallions using different metastable magic structures attached to the wagons. Shocks to be loaded were simply placed into the structure, which lifted it and placed it in the wagon.

Pleased at seeing his theoretical work being put to practical uses, Professor Standar mused, “I did not know that the school had released any of my work for general uses.”

Sande nodded as she strode ahead. Looking back, she replied, “This is an experiment by the Agriculture School and authorized by Dean Honner. If it is as successful as it appears to be, it will be put into general use next year. It should earn both the University and you some handsome royalties.”

“I see. How stable are the structures that they are using?”

Sande grinned as she stated, “They only last about three to four hours. Re setting them takes around twenty minutes, which gives the workers a welcome break. At the moment, it looks like your work has improved harvest efficiency by about 20 to 30 percent.”

By then, they had passed into the village proper. Sande guided them around several turns to a substantial half timbered building with large multi pane windows in front. The sign out front swinging in the breeze proclaimed it to be THE HORN AND HOG.

Inside, the main room was only lightly crowded but it was filled with the beery scent of fermented locoweed. The lanterns and iron candle candle sconces cast a reasonable amount of light. It was late enough that the windows contributed almost none. There were soot trails up the walls above the wrought iron candle sconces. The floor was flaked bark, comfortable underhoof.

They crossed the room, dodging around tables where many disreputable looking unicorns were busy losing what money they had in assorted card and dice games. A few were winning. Not many. Mares in skimpy attire were lacing their way through the press of customers, carrying large trays filled with drinks or dishes of food.

Sande led them to a door and held it open for professor Standar. The back room was far quieter. Many unicorns, both mare and stallion, were standing around five tables. A sixth table was in use. A large bookshelf next to it had holes where volumes now on the table were being consulted and pages of notes being taken.

Dean Honner looked up with a big smile. “Sande! We were waiting for you! The vote went to the Tomb River Campaign. We were just setting up the Crane Creek battle to kick things off! Which side will you take?”

Without hesitation, Sande replied, “South Plains! We beat them so bad in that one that fighting it from their side will be fun! What do I have to work with, General?”

Dean Honner commented to Professor Standar, “The kids know that I was a General in this very war, so the whole club calls me General.”

He handed Sande a sheaf of papers. “Here are your troops and disposition at the start of hostilities. You will find that we actually copied captured scouting reports for you too.”

Sande nodded, while leafing through the data. Breaking into a grin, she put four gold coins in a tray beside one of the game tables. She announced, “Crane Creek table ante is four gold! Pick your staff General and ante up!”

Coins hit the tray. The General and three others took the Wide Plains Republic side of the table. Sande took a wand like pointer and reached into the table top which was a complete reproduction of the Crane Creek battlefield and surrounding area projected by controlled magic. She began to use it to array her forces, which were seriously outnumbered. As he walked about the table, Professor Standar realized just how subtle its design was. From each side, all that could be seen of the opposition was what the field command saw from their place in the old battle or wherever they placed command and scouting for this re fighting of it.

He overheard the General muttering to his three subordinates, “Just as I suspected, she is pulling a fast one on us. I can only see about half of what I saw in real life when I fought this battle! We need scouts out yesterday! Move it!”

One of his assistants muttered back, “I am working on it already. When she said that it would be fun to fight from the South Plains side, I knew that she already had the fix in!”

One muttered, “Found them, I think. That woods that is supposed to be too boggy to get a force through? Three scouts looking it over have vanished.”

The General nodded sagely, “Have to wonder how she got them there, if she did. Probe it in force with a platoon. See what sort of responses we get. Hold the main force in position.”

As he watched the action unfolding, Standar realized that this game was like none that he had seen before. It was not turn based. Both sides were moving simultaneously.

The next report was, “Sir! The platoon was driven off by aimed archery and crossbow fire. The enemy is staying hidden in the forest for now.”

The General gave a satisfied snort. “Crafty of her. Leave a force sufficient to deal with the reserves that she put out for us to see and hit the forest hard. We want to draw her out to better fighting ground if we can.”

As the Wide Plains Republic forces started to strike the boggy forest, Sande's “reserves” began to charge the superior force in front of them. Every copse or thicket that they passed yielded up more disciplined war mares, augmenting the charging army!

They did not simply outnumber the now defending force, they suddenly began a leap frog advance. The pausing forces taking the time to fire an archery barrage into the defenders before rejoining the advance.

By the time that it came to spear and sword, the defenders were severely reduced and quickly cut to pieces! Sande's attack then pivoted and charged the main Wide Plains force from the rear!

The General was swearing in admiration as the trap closed on his troops. They were being forced into the boggy forest and it WAS too swampy for them to hold cohesion as a force.

The Wide Plains Republic had to raise the white flag.

A cheerfully smiling Sande scooped up the table ante and collected a number of side bets as well.

The next battle and the one after that all fell to Sande's skill at warfare.

The golden coins of the Wide Plains Republic antes fell into Sande's purse! She took not only the table antes, she collected side bets in profusion.

The club members were conferring with the General and had three military histories out on a working table. Sande looked over their shoulders and exclaimed, “The Hardrock Chasm Stand! That is one of the best classical battles. The Wide Plains Republic army was outnumbered over one hundred to one! In spite of that they held off South Plains for six days, until reinforcements could arrive and drive South Plains back!”

The General looked up from his books and asked skeptically, “I presume that you have had some thoughts on the battle? Nobody has ever held any simulation where South Plains could get through the Wide Plains Republic position!”

Sande batted her eyelashes at him and retorted, “Finally, a chance for you recover your gold! I mean, I do have South Plains for the battle. This battle will wrap up the Tomb River campaign.”

One of the General's staff commented, “Sande has already stood military history up on its horn. All that I can say is that I think that she must have something nasty up her sleeve!”

Mildly, the General replied, “She always does. Even when she loses, it is usually a disaster for the winning side.”

He set up his troops in the classical and time tested way, camped just in front of the Hardrock Chasm, with the small river to his left. Tall cliffs spread out for twenty miles on each side of the chasm, creating a solid barrier to the South Plains army.

From his camp, the General's forces could strike the South Plains forces in the rear if they tried to bypass the barrier. If South Plains tried a direct attack, all that the Highland Republic had to do was retreat into the chasm itself and South Plain's greater numbers were nullified.

Sande advanced her forces in the classical way, directly out of the histories. She encamped by a small woods. While some troops were cutting firewood, she sent emissaries to request the surrender of the Highland Republic. That was refused, of course.

That afternoon of battle table time, Sande sent a substantial force against the General's troops. She had a strong center that forced battle. From each side, parallel to the cliff faces pincher forces advanced, trying to cut the General's army off from retreating into the Hardrock Chasm.

Just as in history, the ploy failed and the Republic army withdrew into the steep sided and very narrow cleft.

Sande's troops withdrew to their camp, leaving only a few platoons to keep the General bottled up. They had a leisurely meal and replaced the guarding platoons so that they could eat. She was keeping her wood cutters busy apparently making firewood to last out the siege.

On the second battle table day of the battle, Sande advanced the results of her woodcutter's labor. Three catapults. They fired sacks of smaller stones that burst on hitting! The rupturing bags scattered a deadly spray of stones from fist sized up to melon sized chunks through the General's middle ranks! Worse, they then fired at the opening of the chasm, bottling the General's troops, preventing them from escaping the deadly hail of stones, by fleeing deeper in the declivity. She mopped up the remains of his leading forces and advanced into the defile, foot leading, catapults following. As swiftly as her advance made contact with the General's now retreating troops, more catapult shots leapfrogged over them to cut a small number off from aid while they they were reduced. The catapults did not even have to aim much. Hitting a wall of stone simply burst the bag of rocks earlier and blasted them down from above!

Helplessly watching his army dwindle before his eyes, the General quietly reached over to the table ante tray and gallantly handed it over to Sande. He offered, “Brilliantly done, Sande!”

Sande, eyes sparkling with glee, went through the crowd collecting her side bets!

An unfamiliar figure entered the room and scanned the crowd before homing in on Sande. He made the mistake of grabbing her shoulder as he declared, “I demand Herd Rights! You have to mate with me and give me half of that gold you collected tonight!”

Sande rolled in under his grip, striking up along his extended arm, directly into his armpit. Her strike carried enough force that it lifted him off his hooves and laid him full length on the floor!

Sande hit him with both knees in his gut, driving the wind from him. Her right hand slapped the bottom of her shoulder bag and came away with a big combat knife! She held it before his unbelieving eyes so that he could not mistake what it was before she plunged it into his throat!

Conversationally she stated, “If you lie very still, you will live. If I slash even a little to right or left, you will die.

“You cannot claim herd rights on me. I am a herdless mare. My herd was Greenswale. Greenswale was forcably absorbed by the Know Nothing herd who then declared Greenswale to be extinct. There is no Greenswale herd, so you have no Herd Rights on me.

“If your Stallion Need is great enough that it will not be denied, speak to either Wilton or Lanni behind the bar. One of their serving mares will sell you an hour or a night, depending on how much you pay.

“You have nothing more to say to me at all. Speak another word to me and you die. Now, either go away or go to the bar.”

Sande withdrew the knife and backed away from the fallen stallion, maintaining a combat guard with her knife. He got to his hooves, pressing one hand to the cut in his throat, and bolted for the safety of the night.

Sande turned to the shocked club and shrugged. “I know that most mares will yield Herd Rights to just about any stallion in Need. Herd Law is clear, though. Only Herd Stallions can demand Herd Rights of a mare. Other Stallions can ask for Herd Rights but no mare not of their herd is obligated to give them.

“My herd was Greeswale. They were forcibly absorbed by the Know Nothing herd and declared extinct as a herd. He was a scout from the Know Nothing herd. I don't like them because of what they did to my herd. I don't have to mate with them and I WON'T.”

Sande's horn lit up as she used its magic to straighten up the room where the stallion had fallen. She extended a hand to the General and suggested, “General, we need to end this meeting. He was scouting for the Know Nothing Herd. We have to get back to the University and begin preparing our defenses.

“Oakenfield is the last university or college left. If we fall, all of Wide Plains Republic will follow South Plains into an intellectual and physical disaster. We have the last major library. All of our classical literature and research work is in it. We are the last place where magic is being studied scientifically. Our Agricultural School is vital too.

“We have to save as much of it as possible.”

The General gave a sad look around the War Game Club and nodded. “You are right, Sande. I had hoped to never have to fight a real battle again. It is not to be. Anyone here who is willing to fight to save the University, follow us. We are going back to the school.”

Sande was pleasantly surprised to find that nearly all of the rough stallions and mares from the Horn and Hog were following. She could hear much of their muttering, “School might be out of my league but those new higher yield crops sure ain't. Showed us how to use our magic in a whole new way this year at harvest. Got the whole crop in days earlier than the old ways. That school been a godsend to us.”

They were several hundred followers strong by the time that they reached the University.

#THE FALL OF OAKENFIELD UNIVERSITY #Classical Fantasy #Work In Progress #Written by De Writer

5 notes · View notes