#Cayley's theory

[girl-debord]

"A radical monopoly exists where all alternatives have been rendered either inaccessible or unimaginable. An obvious example is an environment in which one simply can't live without a car. What Illich calls 'natural competence' is ruled out. The ability to walk is of no use if your destination is on the other side of a freeway you can't get across; your skill in performing a job is of no consequence if you don't possess the required educational certificate."

- David Cayley, Ivan Illich: An Intellectual Journey

[physicsforever]

Derivation of Cayley Hamilton Theorem I Using Adjoint Matrix I PGTRB I P...

[nezumikozo6th]

April 15th is the Helicopter Day of Japan.The first practical helicopter was the Vought-Sikorsky VS-300,which first flew in the United States on September 14, 1939,but April 15th is actually the birthday of the famous painter and inventor Leonardo da Vinci,who drew the famous design sketch that is considered the prototype of the modern helicopter.However,people's exploration of the aerodynamics behind helicopters can be traced back to at least 1700 years ago.

The bamboo-copter is a ancient toy helicopter rotor from China,which is probably originated in Jin dynasty China around 320 AD.It consists of a shaft and propellers,and the shaft is rotated by friction between the palms of both hands,thereby generating lift for the propeller and making the toy fly into the air.In addition to being perhaps the first tangible device for what is generally understood as a helicopter top,the greatest contribution of bamboo-copter was that after it entered Europe,it inspired George Kelly and others to study modern aviation technology.That flying toy attracted George Cayley,the inventor of modern aeronautics,that made he began experimenting with helicopter tops in 1792,and copied and modified bamboo-copter in 1796.In 1835 Cayley remarked that while the original toy would rise no more than about 6 or 7.5 metres,his improved models would mount upward of 27 metres into the air.

Today, the modern form of the bamboo dragonfly is still used as a toy,especially in Asia that after Doraemon series has brought it back into popularity.

Although bamboo-copter inspired the theoretical basis of modern helicopters,there is no evidence or theory that it can carry humans into air on its own,at least from the past to the 21st century.

By the way,a Japanese science writer pointed out that the Hopter(Doraemon's bamboo helicopter) is either not powerful enough to carry people in flight or will cause harm to the user due to the reaction force.Later,the official explanation was that the hopter actually rises by anti-gravity,and the effect acts on the entire object,not just the contact surface between the hopter and the object.It's not so much to being a miracle of aerodynamics or propeller flight,it is more of a "failure" case.

[coming-up-with-usernames-is-hard]

PhD Blog Week 4

Reading

Kac and Raina bombay lectures, read half of chapter 4, it seems to make more sense than Date's book but that might just be because the notation is closer to what my supervisor uses and I've already seen the explanation once now

Courses

Lie theory: Proved Engel's theorem and looked at Lie's theorem, introduced the Killing form

CFT: SO MUCH QFT. Supposedly QFT is not a prerequisite for this course but if I hadn't already spent a whole year studying QFT I'm not sure how I would have followed anything in this lecture. We're taking an axiomatic approach which is essentially "correlators exist and have these nice properties", and then we introduced path integrals and showed they had the same nice properties, so I guess they can be the same thing. Of course path integrals are badly defined and don't make any sense, but it's fine, you just believe that path integrals and functional derivatives work like normal derivatives and it all works out fine. No actual CFT this time, the conformal symmetry should come in the next lecture

Differential Topology: Painfully detailed calculation of the tangent space to S¹, defined a vector field. Really wish we were using derivations as the basis of our definitions, alas I have to deal with equivalence classes of elements of a disjoint union. It's a weird definition of the tangent space because it presupposes that it's a vector space of dimension equal to that of the manifold. Plus, it's so notation heavy. We're explicitly working with equivalence classes of pairs of a label of a chart and a vector in ℝⁿ and everything is just nested brackets. When I've seen this material previously the goal has always been to drop as much notation as possible and forget any equivalence classes that may be taking place and just work with a representative

Talks

Example showcases started this week, we each have to give a 30min talk about an "example" relevant to what we're researching. We saw four this week, all of which were good. The first was on moduli spaces of flowlines, I followed what was happening but I didn't quite get the point of what we were doing. The second was on surgery theory, I think I got the idea but I've got absolutely no clue on any of the details. The third was on dual Artin groups, which are related to Artin groups (although the "dual" is misleading, there's no duality) and Artin groups are related to Coxeter groups, which I know a little about because Coxeter diagrams are related to Dynkin diagrams and Dynkin diagrams are related to Lie algebras which are nice. The fourth was on CAT(0)-spaces and CAT(0)-groups. I went into this with no idea what a CAT(0)-space is and now I feel I have a good idea, and there was a nice way to think of the free group as moving different parts of its own Cayley graph into focus which reminded me of zippers in type theory, where a zipper is the derivative of the type, which feels like some black magic where you start differentiating objects formed from (co)products in a category as if they were normal polynomials.

My example showcase is next week, so I've started planning that. Currently planning to focus on how we can take inspiration from physics to discover things in maths, but that might all change once I write the talk and work out if it fits in 30min

Supervisor Meeting

Met with my supervisors, most of the meeting was spent looking at different ways to represent the Clifford algebra of fermions. One way was as an infinite tensor product of copies of ℂ² on which Pauli matrices act, the other was as the exterior algebra of an infinite dimensional space where the basis consists of single-fermion states and the wedge product gives us all of the required anticommuting properties. Still have some sign ambiguity between different soruces that I've yet to track down. Also did an example of the boson algebra acting on the Maya diagrams which clarified some misconceptions I had from the previous meeting

Reading Groups

Complex Geometry: We finished off the proof of the Bruhat decomposition and I followed most of it, it's just when it comes to putting it all together that I get lost. I decided I wouldn't be able to give the talk next week, I just don't know enough algebraic geometry and don't have the time to learn it

Infinity Categories: Looked at infinity groupoids (I understood these ok) and how they're the same as Kan complexes (don't understand these). So far it's a lot of drawing simplices and then filling them in. Similar to complex geometry, each step follows but putting it all together I get lost in the details

Categories: Normal 1-categories seem easy in comparison, after missing the first week which clashed with infinity categories the second week we looked at duality and functors

Teaching

TA'd two first year tutorials this week. The problem sheet this week was much harder than the first two, mostly because the questions weren't written very clearly.

I was assigned marking from two courses this week. Marked about 40 assessments, which took about 6 hours. I could go faster if I wrote less feedback but I think the feedback is useful while I have the time to give it. That said it would be nice not to have to write "underline vectors" ever again

[anumberofhobbies]

Also today, we teach that the theories of Sir Isaac Newton (1642-1726) and Swiss mathematician Daniel Bernoulli (1700-1782) provide the detailed science that explains lift. They don’t, at least not fully. The basic problem is that neither theory completely explains real-world observations. Bernoulli’s principle—that the faster air on top of the wing experiences reduced pressure—is correct but doesn’t explain why it’s correct. It also doesn’t explain inverted flight. That’s where Newton’s second and third laws (see the sidebar below for details) come into play. Taken together, Newton’s laws describe how we can fly inverted and how angle of attack works. But they don’t have the details we need from Bernoulli. Still, once we put Bernoulli and Newton in the same room, then sprinkle some Cayley throughout, we have a working idea of how to build and fly an airplane. But we still don’t know exactly why the air on top of the wing is at a lower pressure than the air underneath it.

By Ben Iannotta | February 2023 Given how deeply air transportation is woven into modern life, it’s surprising that the precise workings of aerodynamic lift remain a topic of debate among the experts. To sort all this out, I met on a video call last month with Paul Bevilaqua, retired from Lockheed Martin Skunk Works, and Haithem Taha of the University of California, Irvine. I learned about several myths and at least one collapsing theory. Here is our discussion, lightly edited and compressed.

[spectrallysequenced]

as you know some things about the baumslag solitar groups - so by extrapolation about geometric group theory - what is your favourite finitely generated infinte group and why?

I had to think about this for a while, but honestly I don't think I have an answer. I asked my friend Jack who is a geometric group theorist, and his answer was F_2, because it's very beautiful (meaning its standard cayley graph is), he likes trees, and because freeness is a very cool and important property. I'll add that as a tree its Gromov Boundary is a cantor set, which are also very cool. Also, the Nielsen Schreier theorem (Which has a beautiful proof using covering spaces) says it contains a copy of every other finitely generated free group.

[atplblog]

Price: [price_with_discount] (as of [price_update_date] - Details) [ad_1] This book gives an overview of research on graphs associated with commutative rings. The study of the connections between algebraic structures and certain graphs, especially finite groups and their Cayley graphs, is a classical subject which has attracted a lot of interest. More recently, attention has focused on graphs constructed from commutative rings, a field of study which has generated an extensive amount of research over the last three decades. The aim of this text is to consolidate this large body of work into a single volume, with the intention of encouraging interdisciplinary research between algebraists and graph theorists, using the tools of one subject to solve the problems of the other.  The topics covered include the graphical and topological properties of zero-divisor graphs, total graphs and their transformations, and other graphs associated with rings. The book will be of interest to researchers in commutative algebra and graph theory and anyone interested in learning about the connections between these two subjects. Publisher ‏ : ‎ Springer Nature Switzerland AG; 1st ed. 2021 edition (2 November 2022) Language ‏ : ‎ English Paperback ‏ : ‎ 538 pages ISBN-10 ‏ : ‎ 3030884120 ISBN-13 ‏ : ‎ 978-3030884123 Item Weight ‏ : ‎ 771 g Dimensions ‏ : ‎ 15.5 x 3.2 x 23.5 cm Country of Origin ‏ : ‎ India Net Quantity ‏ : ‎ 1.0 count Generic Name ‏ : ‎ rug [ad_2]

[themathblogofsashanova]

August 25, 2022: Identity, Symmetry and Permutation, and Corollaries Named After My Favorite Black Holes

Upon starting to read the applications of category theory collected here, I was particularly interested in Corollary 2.2.10, (and not just because it is named partially after my favorite black hole).

Any group is isomorphic to a subgroup of a permutation group.

The reason for this being precisely the application discussed yesterday, wherein instead of referencing "truth" we simply state that preservation of form must occur while there is an actual shift in analytical identity.

I have been particularly fond of the following channel, having attempted to incorporate it in my classwork.

Mathemaniac does a great job of visualizing the mathematics in question, while showing procedural excellence in teaching as well. I highly recommend this channel.

Similar to me, I was particularly interested given my last post in the similarity between permutation and symmetry. Interestingly, not all permutations related to symmetries--in fact an uneven distribution of location change of all the original vertices led to a skew or distortion in the shape, leading to corruption of form. So, Mathemaniac says that what is really meant is symmetry of form and not permutation of form unless you qualify that "integrity of form is not corrupted", and the fact that is implied is not at all something that follows from the term "permutation". Which is fascinating, because this terminological issue is itself a bit of a category issue.

What I also found fascinating is that we use the equitable rotation in relation to the identity point to establish if symmetry has occurred. This doesn't in anyway require centralization, however, centralized calculations can make checking for symmetrical distribution more cost efficient computationally, creating a standard segment that can be replicated from a certain position and iterating that process the amount of sides on the shape.

How does this relate to graph theory? I will continue to answer the original question, while not forgetting yesterday's paper in the meantime. Hopefully tomorrow I can link the applications of category theory and the paper in the same post. Such is my brain on mathematics...extremely hyper itself!

[numb3rth30ry]

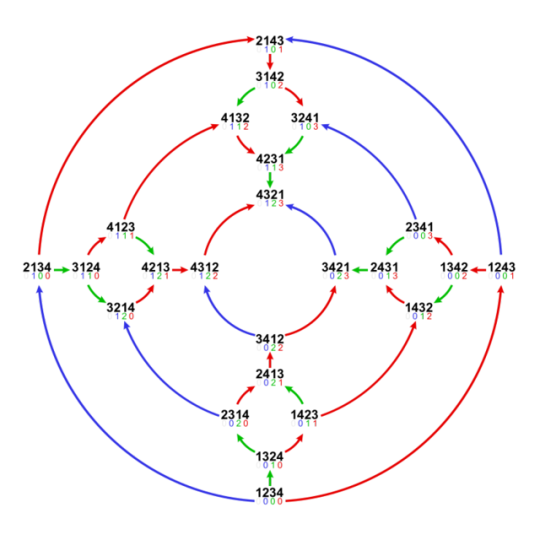
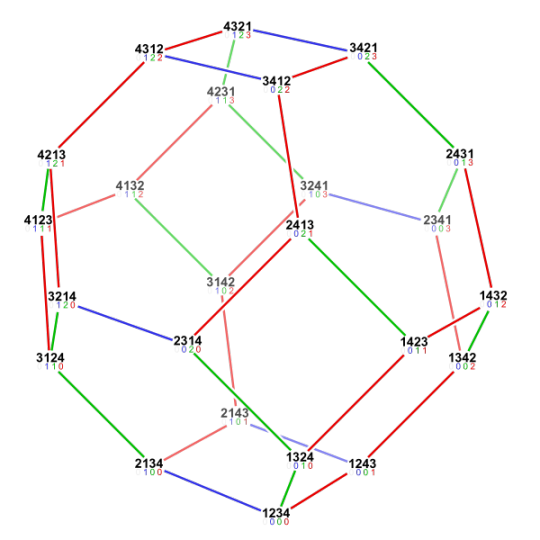
An order 4 permutohedron.

Quoting Wikipedia, “In mathematics, the permutohedron of order n (also spelled permutahedron) is an (n − 1)-dimensional polytope embedded in an n-dimensional space, the vertices of which are formed by permuting the coordinates of the vector (1, 2, 3, ..., n). More generally, the term describes any polyhedron which is the convex hull of a free orbit of the symmetric group Sn acting naturally on R^n. The edge-graph of any permutohedron is the Cayley graph of Sn with respect to the generating set of adjacent transpositions (1,2), . . . , (n − 1,n).”

Mathematics is beautiful. <3

[positivelyapunovexponent-good]

Oooh this looks quite fun! I shall partake. I’m also a bit shy about tagging people but anyone who wants to is welcome to join in!

A couple notes on each of my choices because I have much to say about each of them!

Dungeon Meshi is one of the only pieces of media where I cannot pick a favorite character. At all. I love everyone in the main party + Falin and equal amount and agonised over which character to chose for this poll for frankly too long. Finally settled on Senshi because he’s the most iconic

It was also a little difficult to settle on The Archivist as my favorite character in TMA since the supporting characters are so good, but at the end of the day I cannot resist the incompetent asshole academic who is canonically described as a “grubby Jesus”

I have admittedly been somewhat liberal in what I have interpreted a “character” to be, in my inclusion of real life mathematician Paul Erdős in my poll. However, I stand by my decision, as many would describe him as “a character” in the sense he was quite eccentric. If you don’t believe me PLEASE read his Wikipedia page (or at least the ‘Personality’ section). Seriously it’s one of the few Wikipedia pages I’ve ever read that’s made me laugh out loud uncontrollably. Also - quirks aside- his mathematical work is very cool too! Look up the Erdos Distance problem if you want somewhere to start- mathematicians continue to be chipping away at it in the decades after Erdos’ death. My research advisor once attracted the attention of airport cops after he started jumping up and down with joy in the terminal upon receiving the news that his colleagues significantly improved the exponent of the Erdos distance problem bound. (Honestly he’s kinda a “character” too. )

Okay I now proceed to get even more liberal with the definition of “character” for the purposes of this poll. In particular, the Fourier characters of the cyclic group G = (Z_n, +) are the star blorbos of my thesis. This is because they are QUITE useful for computing the eigenvalues of the adjacency matrix of any Cayley graph on generating set S of G (specifically, the eigenvalues are the sums of Fourier characters evaluated at each of generators in S). Because they are such blorbos to me and literally called characters, I maintain they deserve a place in a character poll

Okay I finally return to a slightly more… ahem… traditional interpretation of “character” in a fandom context. The fandom in question here is my girlfriend’s D&D campaign, so not much of a broad audience. Which is a shame, because it’s WICKED good. If it was a piece of published media widely consumed on tumblr, the character of Ubiquity in particular would have a firmly cemented status as a tumblr sexyman in the most traditional possible sense. I hate the tragic grease stain of a man so much, but I hate him so affectionately that he’s also my favorite. Anyways, my girlfriend’s campaign has been going for years now, and it is by far the “fandom” I spend the most of my creative energy on thinking about- I could theorise for hours, it singlehandedly cured my art block, and I have multiple dumb AUs living rent free in my mind. All that is to say my girlfriend is an absolute world-building genius and one of my favorite writers

inspired by @1tbls et al— no one tagged me but it seemed fun and I want in

if you want to partake, make a poll with 5 of your favorite characters & tag 5 people

however I get Very Nervous about tagging folks in things like this so if you see this just consider yourself invited to join in

[lawsofemotion]

Updated Chapter 9: Isomorphisms!

[coming-up-with-usernames-is-hard]

PhD Blog Week 6

Courses

CFT: Actually more reasonable this week, spent most of the lecture studying the analytic structure of correlators, which just amounts to picking nice conformal transformations to pull out the information needed

Diff Top: The exterior algebra, but in the absolute worst way possible. Now that we're doing something I know about it just makes me wonder how bad the manifolds lectures were. Assessment was released, doesn't look too bad but I think it will take ages

Lie theory: Finished the proof of Weyl's theorem and started on the classification of simple Lie algebras by defining a Cartan subalgebra

Talks

Example showcases: Moduli spaces, started well with a nice example of the moduli space of triangles, then suddenly ramped up and started discussing schemes and I was lost. Hyperbolic groups and their boundaries, nice pictures and impressive drawing on the board of hyperbolic space, the boundary of a group is an interesting concept, it's the boundary of the Cayley graph embedded in hyperbolic space. Knots and finite type invariants, basically defined the Jones polynomial and another type of invariant, impressive live drawings of knots, evaluating the Jones polynomial at e^h and then Taylor expanding the coefficients are these finite type invariants, which is neat, but I'd like to have seen why it's true. Final talk was a physics one, looked at a particular list of conditions that might be desireable for a reasonable spacetime and came up with a contradiction implying that such a reasonable spacetime couldn't exist, it was nice to see someone else doing physics, and fun to think about GR again, which I haven't done for a while.

Supervisor Meeting

Spent half the meeting recapping the previous one for the people who missed it, which was a good test of my understanding, I don't think I did too badly. Then looked at how a simple modification of the rules we had would allow us to achieve equivalent results for other bases than the Schur functions, these rules correspond to adding horizontal and vertical strips (rather than general ribbons) to the Young diagrams, and the resulting lattice has 5 allowed vertices rather than 6, because to block unwanted vertical/horizontal boxes removes one choice

Reading Groups

Complex geometry: Missed it this week, I'll have to read the notes

Infinity categories: Defined limits in an infinity category, spent most of the time defining the join of two simplicial sets, then once you've done this the definition isn't actually that different to a 1-category

Categories: Equivalence of categories

Teaching

Just the two TA sessions this week, we move back to the maths building next week so no more running all over campus

[transgenderer]

i wonder if you could reformulate group theory centered on considering a group primarily in terms of the set (or like, object) that its the automorphism group of rather than thinking of it primarily in terms of its like, cayley table/graph

[locally-normal]

Consider the set of symmetries of a square, a symmetry being some transformation of the square that leaves it looking like the square. If you label the vertices you can see them moving though. There's 8, if you include "do nothing" as a symmetry. That's 3 rotations and 4 reflections, and doing nothing.

Notice you can do one symmetry and then another, and that will be represented by one of your 8 symmetries. You can think of this as a "multiplication" of symmetries. Notice if you switch the order, you may get a different result, the multiplication isn't commutative. Actually do all of these things, math, as they say, isn't a spectator sport. This is the group D4, the dihedral group. There's one for each regular n-gon., and you should work out every possible multiplication for D3, the symmetries of the triangle, and tabulate them in a multiplication table. Actually, using the composition, consider what's a good way to name these symmetries. Is there any more descriptive way than just like f_1,...,f_6? I won't spoil the answer here but wikipedia on dihedral groups will have it if you look hard, math wikipedia can be tough reading. Think about it though.

Now consider the symmetries of the sequence {1, 2, ... n}. Now symmetries are reorderings of the set with n elements, things that leave it the same size but change the order. Actually, do consider the multiplication table for n=3 and see if it feels familiar. How big is it for arbitrary n. This is the symmetric group, you can again compose symmetries. Understanding the symmetric group in detail is very helpful.

Every group is like this. Actually, every finite group is a subgroup of a symmetric group for some n, that's Cayley's theorem, it's super cool. So truly every group is like this.

This is, abstractly, the motivation for group theory, we want to study symmetries.

It's ubiquitous in mathematics. Invariants of shapes, eg, form symmetries, so this is a great way to study shapes and spaces. Groups are all over algebraic topology and geometry for this reason. Really that's the "algebraic" of algebraic topology.

If you want to find roots of a polynomial, you'll notice they often come in pairs, for example the complex roots of a quadratic are conjugate complex numbers. This is actually the symmetric group for n=2, with conjugation as the non-identity symmetry. You can also see this for x^2=2, the roots are +-root 2, those are paired up. For higher degree polynomials you'll also get this behaviour, but you may get more complicated groups of roots. This is Galois Theory, and I think it was the first time groups came into prominence.

Those are just the first two examples I came up with, but groups are absolutely ubiquitous. They model symmetry, but they also just model nice binary operations, since you can compose symmetries. And binary operations, while more abstract, are truly everywhere, we're always putting things together in some fashion.

The integers with addition are a group, a set with a binary operation, as are the integers (excluding 0) with multiplication. If you think of a group this way you need to put some constraints on the operation, to capture the same behavior we had when composing symmetries. These are associativity, having an identity, and invertibility. Notice all the examples at the beginning had these properties (hopefully that's not terribly hard to check by hand if you wrote out the full multiplication table.)

Good luck with group theory, have fun!

What the hell is group theory...

I've tried watching a couple videos about it and I barely understand what it's about TwT

It's so abstract!

I seek your help mathblr, how would you explain group theories to someone who has never had any direct experience with it and how does it play with other fields of math?

The very basic basics I mean ofc (but if you'd like to provide an in depth post I'm not against it)

[thejugheadparadox]

ok i talked abt rossetti + elizabeth siddal’s self portrait as part of my art history final 2 years ago and i am dying to know about christina. please

CHRISTINA ROSSETTI!!! i honestly barely knew anything about the portrait before seeing that post i would love to know more. i am so fascinated by christina georgina rossetti born 1830 died 1894, so she’s like ridiculously quintessentially victorian, she basically never knew another monarch. when she was a child she was angry and had a lot of tantrums, her and her brother the painter one dante gabriel were know as the two storms whilst their others siblings maria and william were known as the two calms (suuch classic irritating twee victorian fake middle class art family shit but i find it faintly endearing). she dropped out of school at the age of 14 due to a religious breakdown, and never went back. during and after that she was really fixated on christianity especially anglo-catholicism and its very specific doctrines. she was REALLY into it in a way the rest of her family werent (except her sister who became a nun i guess). she’d been writing poetry since she was very young, cus she’s from this eccentric art dynasty they played writing games as kids and shit - her maternal uncle was john william polidori who wrote the first published vampire story and was lord byrons doctor if that rings any bells? that relation specifically is sooo interesting to me bc its about legacy and who you are remembered as and whether youre noticed and also maybe youre gay? yk. i love it. 

ANYWAYS. she was so into religion that it stopped her getting married twice. she was engaged to the prb painter james collinson for a bit but broke it off bc he reverted to roman catholicism and she couldnt be doing w that shit. she later got engaged to charles cayley and also broke that off for religious reasons! Or At Least Thats What They Say. she also turned down a possible proposal (ppl dont know if he proposed and the whole affair is a guess) from john brett, which she wrote a fun mean poem about called no thank you john. anyway she never married and she pursued lots of Things but none of them really went anywhere, she wanted to be a nurse w florence nightingale in the crimean war but got rejected, she worked with “fallen women” in her 30s and 40s. shes not one of those tragic figures who never knew fame while they were alive tho, she was pretty successful and released multiple collections. she was publicly antifeminist and declined to sign petitions in support of womens suffrage but wrote this one unpublished poem called from the antique that explicitly expresses her dissatisfaction with her limited life as a woman. 

she got ill lots, as is classic for old timey lady poets, like emily dickinson style. she got depressed lots and after her dad died her family didnt have much money. she wrote a lot about inadequacy, as a woman and as a person and most often as a servant of god (every fucking poem ends up about jesus i swear to god it gets annoying). her brother was more successful and her sister was more devout and she never seemed to get the things she wanted and she never really had any friends, especially female ones. almost every time she was published, it was by her brother, william michael, who also published her works en masse after she died, and we have explicit sources showing both her brothers would tell her not to publish poetry they deemed out of character or unwomanly. i dont mean to entirely demonise them as the Bad Guys of the story but i find it very.... interesting that when u look at her poetry that is available but not officially published there are both feminist poems and a couple of pieces that coiuld be interpreted as love poems towards women. there are (admittedly pretty unfounded as far as i can tell) theories that even more of them existed and were destroyed, but i should say we DO know that there are missing poems and destroyed scraps that pique ones interest i will say!

ive read her collected family letters and what stood out to me is HOW ridiculously fucking boring they are. i think theyre hiding something.. i am fascinated by all of it. she interests me. i have some kind of parasocial relationship with her and i feel like her work is SO easy to translate to modern day and what ppl our age are writing about like she wrote what is essentially lonely notes app poetry about religious guilt and sexual repression and hating herself like. god i sound like those ppl who say dantes inferno is fanfic but i think about it a lot and i think about her a lot and i would recommend a lot of her poetry... if anyone wants specific recs do ask. to me its a story about hiding and repression and wanting to be good. jesus christ okay u did not ask for this but youre getting it. you made me start thinking about her again this is on you. 

[etirabys]

My favorite object-with-visual-features from group theory so far is alternating group A5, which has a Cayley diagram you can draw to look like a soccer ball

and the multiplication table looks like THIS!