#درایه

[sahbaykherad]

‏‎🌷﷽🌷 ▫️همانگونه که می دانید در بررسی و استناد به روایات، اصول و ضوابطی وجود دارد از این رو شخصی که به مطالعه روایات و بررسی آنها می پردازد باید با علومی همچون #رجال، #درایه و #فقه_الحدیث آشنا باشد تا بتواند ضوابط آنها را به کار بسته و به صورت صحیح و روشمند از احادیث بهره ببرد. در حوزه روایات اعتقادی نیز برخی از ضوابط مشترک است نظیر ضوابط رایج علم رجال، که این روایات نیز به همان ضوابط مورد بررسی قرار می گیرند. اما ویژگی های خاصی نیز در این حوزه وجود دارد که در حوزه روایات فقهی چندان اهمیت یا کاربرد نداشته باشد. ما در زیر به اختصار به برخی از مهم ترین ضوابطی که در مطالعه #منابع_حدیثی اعتقادی باید به آنها توجه داشت اشاره می کنیم. البته ناگفته نماند که نکاتی که در زیر می آید، لزوما اختصاص به احادیث اعتقادی ندارد. ۱. عدم اعتبار ظنون در #اصول_دین و اعتقادات در مباحث اعتقادی، آنچه معتبر است علم (یقین و قطع) است نه #ظن و گمان. چنانکه قرآن کریم می فرماید:: «و لا تَقفُ ما لَيسَ لَك به علم؛ از چیزی که بدان علم نداری، پیروی مکن» (سوره اسراء، آیه۳۶) و نیز می فرماید: «إنّ الظنّ لا یُغنی مِن الحقِّ شَيئًا؛ گمان و ظن تو را به حق نمی رسانند»(سوره یونس، آیه ۳۶). اين آيات گمان و تقلید را در حوزه عقاید نهی می کند زیرا در حوزه #احكام_فقهی بنا بر قول مشهور حجّت شرعی است. بر همین اساس در روایات اعتقادی نمی توان به خبر واحد اعتماد کرد. ۲. توجه به شرایط زمانی مکانی صدور حدیث: در مطالعه و تفسیر #روایات معصومین، باید به شرایط زمانی مکانی صدور روایات و نیز فضای فکری عقیدتی و تحولات اجتماعی عصر آن امام توجه داشت. بسیاری از روایات اعتقادی در نقد یا ناظر به نحله های فکری عقیدتی عصر آن امام است. ۳. ضرورت تحلیل و نقد محتوایی‏ ‏‏در اصول دین، یقین معتبر است لذا از میان روایات، تنها روایات متواتر هستند که از حجیت برخوردار می باشد و چنانکه گفته شد خبر واحد و ظن حجت نیست. حال اگر در صورتی که خبر متواتر یا حتی آیات قرآن کریم با حکم قطعی عقل تعارض کنند، باید تاویل شوند از این می توان گفت که در روایات اعتقادی معیار نقد و بررسی آن، عقل است و در روایات اعتقادی، صحت سندی آنها چندان کارگشا نیست. #مدرسه_کلام_اسلامی #علیرضااسعدی 🔹️ادامه مطلب را در صورت تمایل در کانال تلگرام یا ایتا با نام کاربری زیر ببینید: 🆔️ @asaadi99 صهبای خرد‎‏ https://www.instagram.com/p/CFueDqdhX81/?utm_medium=tumblr

[reyson98]

هوش مصنوعی چطور با کووید 19 مبارزه می‌‌کند؟

دکتر یِیل تانگ چن ، پزشک اورژانس مادرید، روز 9 مارس، در توییتی این‌‌طور نوشت: «روز اول پس از تشخیص #COVID. گلودرد، سردرد (شدید!)، سرفه‌‌ی خشک اما بدون تنگی نفس. بدون ناهنجاری در سونوگرافی ریه. #POCUS ریه‌‌هایم را کماکان خواهم گذاشت. #coronavirus» «POCUS» مخفف سونوگرافی نقطه‌‌ی مراقبت است. در زیر این متن عکس سونوگرافی ریه‌‌های چِن گذاشته شده و در گوشه‌‌ی سمت راست پایین تصویر به زبان اسپانیایی نوشته شده است: «عکس‌‌برداری توسط Butterfly iQ.» برخی شرکت‌‌های حوزه‌‌ی بهداشت و سلامت _مثل شرکت نوپای تصویربرداری پزشکی Butterfly Network، سازنده‌‌ی Butterfly iQ منحصراً در واکنش به شیوع ویروس شکل گرفته‌‌اند. Butterfly iQ یک دستگاه سونوگرافی دستیِ قابل حمل است که با هوش مصنوعی کار کرده و تصاویری را برای تفسیر خودکار، به گوشی همراه کاربر می‌‌فرستد. این شرکت نوپا از زمان شیوع کووید-19 در اواسط ژانویه در منطقه‌‌ی آسیا پاسیفیک، آن را زیر نظر گرفته بود، همان جایی که پزشکان اهمیت تصویربرداری ریه در دنبال کردن و درمان این ویروس را گوشزد می‌‌کردند. از آنجا که اسکنر Butterfly Network می‌‌توانست به‌‌عنوان یک پاک‌‌کننده (cleaner) عمل کند، جایگزین ارزان‌‌تری نسبت به اشعه‌‌ی ایکس و سی‌‌تی اسکن بود، اهمیت این محصول از قبل برای شرکت روشن شده بود. بعد از اینکه توجه شرکت نوپای مذکور به پزشکانی مثل چِن جلب شد که تصاویر ریه‌‌های آلوده را در رسانه‌‌های اجتماعی به اشتراک می‌‌گذاشتند، یک صفحه‌‌ی فرود راه‌‌اندازی کرد که کارشناسان سلامت می‌‌توانستند در آن تصاویر خود را به اشتراک گذاشته و نحوه‌‌ی استفاده از اسکنر برای سونوگرافی ریه را یاد بگیرند. سه‌‌شنبه‌‌ی گذشته Butterfly Network میزبان یک وبینار هم بود تا به فعالان حوزه‌‌ی سلامت در جهت تشخیص ریه‌‌ی مبتلا به کووید-19 کمک کند. هوش مصنوعی به دو شکل وارد بازی می‌‌شود. اول، تجزیه‌‌وتحلیل خودکار تصویر، استفاده‌‌ی مؤثر از اسکنر را برای افراد کمتر آموزش‌‌دیده آسان‌‌تر می‌‌کند. از آنجا که بیمارستان‌‌ها به‌‌منظور مدیریت هجوم بیماران، وظایف کارکنان خود را تغییر می‌‌دهند، کارمندان ناآشنا به تفاوت‌‌های ظریف تصاویر ریه می‌‌توانند بیماران را غربالگری کرده و از یک دستگاه قابل‌‌دسترس‌‌تر بهره ببرند. دوم اینکه، طبق ایمیل مدیر آموزشی، دکتر مایک استون و افسر ارشد پزشکی، دکتر جان مارتین ، از آنجا که کارشناسان حوزه‌‌ی پزشکی که تخصص بیشتری دارند از اسکنر Butterfly به‌‌منظور بررسی علائم کووید-19 استفاده می‌‌کنند، سیستم ابر-محور شرکت، داده‌‌های قوی‌‌تری درمورد ویروس و رفتار آن به دست خواهد آورد و این در نهایت، تجزیه و تحلیل محصول را دقیق‌‌تر و درست‌‌تر می‌‌کند. مارتین این مطالب را حین مکاتبه با متخصصان اورژانس در چین، ایتالیا، اسپانیا، و انگلستان و در بحبوحه‌‌ی افزایش همه‌‌گیری نوشته بود. در این ایمیل این‌‌طور گفته شده: «در حال حاضر در این رویکرد همه‌‌ی-گزینه‌‌ها-روی-میز است.» البته همان‌‌قدر که درمان افراد مبتلا اهمیت دارد، باید مطمئن شد که آنها افراد بیشتری را آلوده نمی‌‌کنند. Biofourmis، شرکت نوپای واقع در بوستون، یک پلت‌‌فرم تحلیل سلامت به نام Biovitals ارائه می‌‌دهد که با هوش مصنوعی کار کرده و از رصد کردن بیماران به‌‌منظور پیش‌‌بینی مشکلات سلامتی قبل از وقوعشان بهره می-برد. Biofourmis در پروژه‌‌ی راهکار رصد کردن قلب در خانه، دو سال با دانشگاه هونگ‌‌کونگ همکاری کرده بود که با تماسی از طرف دولت محلی و درخواستی مبنی بر این مواجه شد که آیا می‌‌توان راهکار پیش‌‌گفته را برای رصد کردن کووید-19 در خانه هم به کار برد. این مساله به این خاطر است که تأسیسات بهداشت و سلامت یکی از ناامن‌‌ترین مکان‌‌ها برای بیماران در دوران همه‌‌گیری هستند. در ماه فوریه، در 7 مطالعه بر روی 138 بیمار مبتلا به ویروس کرونا در ووهان چین، 41 درصد مشکوک به گرفتن ویروس در بیمارستان بودند. با نگهداری ناقلین و ناقلین احتمالی در منزل، کادر درمان و بیماران آسیب‌‌پذیر بیمارستان، از قرارگیری در معرض خطر مصون می‌‌مانند. Biofourmis تماس مذکور را اواسط ماه فوریه دریافت کرد. از راهکار او دو هفته قبل در هنگ‌‌کنگ رونمایی شد. راهکار مورد بحث به این شکل کار می‌‌کند: بیمارانی که مثبت، یا در خطر ابتلا به کووید-19 هستند، به یک حسگر زیستی مجهز می‌‌شوند که روی یکی از دستان آنها قرار می‌‌گیرد، و سپس به خانه فرستاده می‌‌شوند. این حسگر، 20 سیگنال متفاوت فیزیولوژیک را از طرف شخص دریافت می‌‌کند؛ ازجمله دما، ضربان قلب، و آهنگ تنفس. از سوی دیگر، بستر Biofourmis از هوش مصنوعی به‌‌منظور تجزیه و تحلیل سیگنال‌‌ها و تشخیص نیاز به تماس با پزشک استفاده می‌‌کند. مدل یادگیری ماشینی به مرور زمان شروع به فهم امضای فیزیولوژیک ویروس خواهد کرد تا در حالت آرمانی بتوان آن را زودتر شناسایی، و مؤثرتر درمان کرد. کولدیپ سینگ راجپوت ، مدیرعامل Biofourmis این‌‌طور می‌‌گوید: «ما همین‌‌حالا در حال جمع‌‌آوری داده‌‌های مربوط به دارو، تصویربرداری، اطلاعات بالینی و درمان هم هستیم، و می‌‌توانیم از هوش مصنوعی بهره گرفته و بیشتر درمورد این بیماری بیاموزیم، چرا که در حال حاضر اطلاعات بسیار کمی در این باره داریم. وقتی هوش مصنوعی ما را راهنمایی کرده و دقیقاً به ما بگوید کووید-19 چه امضایی دارد و چطور پیشرفت می‌‌کند، به پزشکان در مدیریت بهتر بیماران کمک خواهد شد، البته شرکت‌‌ها را هم در رسیدن به راهکارهای جدید یاری خواهد کرد.» به گفته‌‌ی راجپوت، هفته‌‌ی آینده، بستر پیش‌‌بینی Biofourmis در سه کشور دیگر هم که آمار ابتلا به کووید-19 در آنها بالاست، آغاز به کار خواهد کرد. وی افشا نکرد که کدام سیستم‌‌های بیمارستانی در این برنامه شرکت خواهند کرد. برخی شرکت‌‌ها که از هوش مصنوعی برای کمک استفاده می‌‌کنند در حیطه‌‌ی فن‌‌آوری سلامت نیستند. درواقع، آنها حتی الگوریتم‌‌های خودشان را نمی‌‌سازند. CRITICALSTART یک شرکت نوپای امنیت سایبری اهل تگزاس است. مدیر خدمات حرفه‌‌ای آن یعنی کوئنتین رودز ، به قول خودش دوست دارد در همه‌‌ی کارها بهترین –یا حداقل نزدیک به بهترین- باشد. او می‌‌گوید: «من تقریباً در هر کاری که انجام می‌‌دهم اهل رقابتم. هیچ‌‌وقت نمی‌‌خواهم عقب بیافتم. حدس می‌‌زنم همیشه همین‌‌طور بوده‌‌ام.» شاید به همین خاطر باشد که وقتی کاربر توییتر @TinkerSec پیامی به او فرستاد که می‌‌گفت یکی از پژوهشگران ساختارهای پروتئین کووید-19 را شبیه‌‌سازی کرده، رودز همان‌‌روز با شرکت او قرارداد بست. این پروژه Folding@Home نام داشت که اقدامی از سوی پژوهشگران دانشگاه واشنگتن در دانشکده‌‌ی پزشکی سنت لوئیس برای منبع‌‌یابی جمعی قدرت رایانشی مورد نیاز برای راه‌‌اندازی شبیه‌‌سازی‌‌های بسیار پیچیده‌‌ی اتم-های ویروس‌‌ها بود. ویروس دارای پوشش پروتئینی متشکل از آمینو-اسیدهای فشرده‌‌ای است که از اتم تشکیل می‌‌شوند. روش‌‌های آزمایشی موجود، تصویری فوری از اتم‌‌های ویروس تهیه می‌‌کنند، اما هیچ اطلاعاتی از نحوه‌‌ی حرکت و تعامل آنها ارائه نمی‌‌دهند. شبیه‌‌سازی، روش بهتری برای شکار نقطه‌‌ضعف‌‌های ویروس است، اما انجام هر شبیه‌‌سازی، محاسبات زیادی لازم دارد –که انجام آنها بر روی یک رایانه صدها سال زمان خواهد برد. در اینجاست که سرور رمز-شکن CRITICALSTART به نام Cthulhu وارد بازی می‌‌شود. Cthulhu ترکیبی از سخت‌‌افزار و نرم‌‌افزار است که از هشت کارت گرافیکی Nvidia Titan V استفاده می‌‌کند –که برای یادگیری عمیق و تحقیقات هوش مصنوعی ساخته شده- تا در هر ثانیه 27.8 بیلیون گذرواژه را حدس بزند. فهرست‌‌های احتمالات-گذرواژه‌‌ای آن که به‌‌صورت خودکار تهیه می‌‌شوند، حاوی کوادریلیون درایه‌‌ی منحصربه‌‌فرد هستند. با به کار انداختن Cthulhu، CRITICALSTART بیش از 240،000 گروه در سرتاسر جهان را به هم پیوند داد تا تجهیزات رایانشی قدرتمند، یا حتی لپ‌‌تاپ‌‌های شخصی را وقف انجام این کار کند. به گفته‌‌ی دکتر گرگ باومن در توییتر، در هفته‌‌ی منتهی به 18 مارس، 400،000 نفر Folding@Home را بارگیری کردند، و حالا این پروژه 470 پتافلاپ قدرت در اختیار دارد یعنی بیش از دو برابر قدرت نهایی ابَررایانه‌‌ی Summit. (Summit سریع‌‌ترین رایانه‌‌ی جهان است. تا به‌‌حال با انجام شبیه‌‌سازی، 77 درمان احتمالی ویروس کرونا را پیدا کرده است.) یک هفته بعد از راه‌‌اندازی Folding@Home، رادز کماکان رتبه‌‌بندی شرکت خود را دقیقاً دنبال می‌‌کند. وی می‌گوید «همین حالا ما در میان دو درصد برتر از شرکت‌‌کنندگان قرار داریم و این خیلی دیوانه‌‌کننده است. منظورم این است که ما هنوز در جهان تقریباً پنج‌‌هزارمین شرکت محسوب می‌‌شویم، البته هنوز.» به گفته‌‌ی رادز، گروه CRITICALSTART شبیه‌‌سازی را فعلاً متوقف کرده تا چند مرتبه آزمایش نفوذ انجام دهد، ولی GPUها (واحدهای پردازش گرافیکی ) عمدتاً به تولید داده پیرامون ویروس اختصاص یافته‌‌اند. در شرایط بحرانی، انجام کار مفید، حس خوبی دارد و رتبه‌‌بندی‌‌های گروه چندان اهمیتی ندارند. رادز می‌‌گوید «این کاری برای انجام دادن به گروه ما می‌‌دهد که سودمند است. ما سعی داریم دیگر رقبای خودمان را متقاعد کنیم تا آنها هم در این کار سهیم شوند. این تا حدی قواعد بازی را وارد کار می‌‌کند و به ما اجازه می‌‌دهد نه‌‌تنها در یک هدف خوب سهیم باشیم، بلکه حق رجزخوانی را هم به دست آوریم.» آیا هوش مصنوعی می‌‌تواند به پیش‌‌بینی همه‌‌گیری بعدی در جهان کمک کند؟ علی‌‌رغم فایده‌‌ی هوش مصنوعی برای پژوهشگران، کارکنان بهداشت و سلامت و انواع شرکت‌‌ها، این فن‌‌آوری محدودیت‌‌های خودش را هم دارد. به‌‌عبارتی، وابستگی‌‌اش به داده‌‌های گذشته، آن را به ابزاری ناکامل برای واکنش نشان دادن به یک تهدید جدید تبدیل می‌‌کند. وقتی بحث از کووید-19 به میان می‌‌آید، هوش مصنوعی نمی‌‌تواند به ما بگوید که بعد از آن چه اتفاقی خواهد افتاد و واقعاً هم به ما نگفته در حال حاضر چه اتفاقی رخ می‌‌دهد. به‌‌عنوان مثال، به گزارش Vox یک متخصص یادگیری ماشینی که از طرف مراکز کنترل و پیشگیری بیماری برای مدل‌‌سازی عفونت‌‌های فعلی مورد استفاده قرار گرفته، ترجیح داده از یادگیری ماشینی استفاده نکند. درعوض از روشی موسوم به «خرد جمعی» بهره می‌‌گیرد که در آن افراد عادی گزارش می‌‌دهند که به نظرشان همه‌‌گیری چطور در حال گسترش یافتن است، و پژوهشگران پاسخ‌‌های آنها را برای مدل‌‌سازی، گردآوری می‌‌کنند. به گفته‌‌ی گابریل موسو، افسر ارشد علمیِ BioSymetrics که در نیویورک سیتی واقع شده، «اولین سؤالی که هر کسی خواهد پرسید این است که چطور از وقوع دوباره‌‌ی این اتفاق جلوگیری کنیم؟ به نظر من این مسئله مورد توجه زیاد و شایسته‌‌ای قرار خواهد گرفت.» BioSymetrics یک بستر هوش مصنوعی است برای کشف دارو در مراحل ابتدایی. به گفته‌‌ی موسو شرکتش مشتریان زیادی دارد که از یادگیری ماشینی به‌‌‌‌منظور کشف داروی مربوط به کووید-19 یا پروژه‌‌های دارای اولویت درمانی استفاده می‌‌کنند. آن‌‌طور که موسو می‌‌گوید، هرچند شاید مدل‌‌های یادگیری ماشینی نتوانند جلوی شیوع ویروس بعدی در جهان را بگیرند، اما معنایش این نیست که آنها نمی‌‌توانند در آماده‌‌سازی بهتر ما نقش داشته باشند. تشخیص تازگی ، حوزه‌‌ای از یادگیری ماشینی است که در آن مدل یاد می‌‌گیرد سیگنال‌‌ها یا داده‌‌هایی را که بخشی از یادگیری‌‌اش نبوده‌‌اند تشخیص دهد. مثلاً مدلی که برای تشخیص سیگنال‌‌های یک انسان سالم آموزش دیده، می‌تواند علائم اولیه‌‌ی بیماری را تشخیص دهد. هرچقدر که مدل بیشتر بفهمد کدام علائم به بیماری منجر می‌‌شوند، زودتر می‌‌تواند علائم هشداردهنده را تشخیص دهد. روزی می‌‌رسد که همین اتفاق درمورد همه‌‌گیری‌‌ها بیافتد.

https://reyson.ir/?page_id=20

[mthmtc]

دترمینان یک ماتریس

New Post has been published on https://mthmtcs.ir/determinant/

دترمینان یک ماتریس

دترمینان ماتریس مربعی، که به صورت $ \vert A \vert $ یا $ det( A ) $ نمایش داده می‌شود، یکی از مفاهیم مشهور جبر خطی است که کاربردهای بسیاری در علوم مختلف دارد. امکان محاسبه‌ی سریع دترمینان یک ماتریس با ابعاد بزرگ بحث مهمی است که در ادامه سه روش محاسباتی رایج و پیچیده‌گی زمانی آنها مرور خواهند شد.

    طبق تعریف دترمینان اگر اندازه‌ی ابعاد ماتریس مربعی یک باشد ($n = 1$) ، دترمینان همان مقدار تک‌عضو آن است. یعنی:

\[ det( \beginbmatrix a \endbmatrix ) = \vert \beginbmatrix a \endbmatrix \vert = a \]

    اما اگر مرتبه‌ی ماتریس بزرگتر از یک باشد ($n > 1$) دترمینان را به یکی از روش‌های زیر می‌توان محاسبه کرد.

\[ A_n \times n = \beginbmatrix a_11 & a_12 & \cdots & a_1n \\ a_21 & a_22 & \cdots & a_2n \\ \vdots & \vdots & \ddots & \vdots \\ a_n1 & a_n2 & \cdots & a_nn \endbmatrix \]

بسط لاپلاس دترمینان

بسط لاپلاس (یا بسط همسازه‌ای) برای محاسبه‌ی دترمینان ماتریس مرتبه‌ی $n$ ، به فرم زیر است:

\[ \vert A \vert = \sum_j=1^n (-1)^i+j a_ij \vert A_ij \vert \qquad , \qquad 1 \leq i \leq n \]

    یا

\[ \vert A \vert = \sum_i=1^n (-1)^i+j a_ij \vert A_ij \vert \qquad , \qquad 1 \leq j \leq n \]

    که در حالت اول بسط بر اساس سطر دلخواه $i$ و در حالت دوم بر اساس ستون دلخواه $j$ صورت گرفته است. منظور از $A_ij$ ( ماتریس کهاد) ماتریسی است که از حذف سطر $i$ ام و ستون $j$ ام ماتریس اصلی به دست آمده است.

    به عنوان مثال اگر ماتریس مربعی $A$ به صورت زیر تعریف شده باشد:

\[ A = \beginbmatrix 1 & -1 & 8 \\ 0 & 3 & 1 \\ 2 & 2 & 1 \endbmatrix \]

    دترمینان آن با بسط روی سطر اول به این ترتیب محاسبه می‌شود:

\[ \beginvmatrix 1 & -1 & 8 \\ 0 & 3 & 1 \\ 2 & 2 & 1 \endvmatrix = (-1)^1+1 \times 1 \times \beginvmatrix 3 & 1 \\ 2 & 1 \endvmatrix + (-1)^1+2 \times (-1) \times \beginvmatrix 0 & 1 \\ 2 & 1 \endvmatrix \] \[ + (-1)^1+3 \times 8 \times \beginvmatrix 0 & 3 \\ 2 & 2 \endvmatrix = 1 \times \Big((-1)^1+1 \times 3 \times \vert 1 \vert + (-1)^1+2 \times 1 \times \vert 2 \vert \Big) \] \[ + 1 \times \Big((-1)^1+1 \times 0 \times \vert 1 \vert + (-1)^1+2 \times 1 \times \vert 2 \vert \Big) \] \[ + 8 \times \Big((-1)^1+1 \times 0 \times \vert 2 \vert + (-1)^1+2 \times 3 \times \vert 2 \vert \Big) \] \[ = 1 \times( 3 – 2 ) + 1 \times ( 0 – 2 ) + 8 \times ( 0 – 6 ) = 1 – 2 – 48 = -49 \]

    و با بسط روی ستون دوم:

\[ \beginvmatrix 1 & -1 & 8 \\ 0 & 3 & 1 \\ 2 & 2 & 1 \endvmatrix = (-1)^1+2 \times (-1) \times \beginvmatrix 0 & 1 \\ 2 & 1 \endvmatrix + (-1)^2+2 \times 3 \times \beginvmatrix 1 & 8 \\ 2 & 1 \endvmatrix \] \[ + (-1)^3+2 \times 2 \times \beginvmatrix 1 & 8 \\ 0 & 1 \endvmatrix = 1 \times \Big( (-1)^1+2 \times 1 \times \vert 2 \vert + (-1)^2+2 \times 1 \times \vert 0 \vert \Big) \] \[ + 3 \times \Big( (-1)^1+2 \times 8 \times \vert 2 \vert + (-1)^2+2 \times 1 \times \vert 1 \vert \Big) \] \[ – 2 \times \Big( (-1)^1+2 \times 8 \times \vert 0 \vert + (-1)^2+2 \times 1 \times \vert 1 \vert \Big) \] \[ = 1 \times( -2 + 0 ) + 3 \times ( -16 + 1 ) – 2 \times ( 0 + 1 ) = -2 – 45 -2 = -49 \]

    توجه داشته باشید که منظور از $\vert \; . \vert $ علامت قدرمطلق نیست.

    انتخاب سطر یا ستون مناسب برای محاسبه‌ی دترمینان با استفاده از این روش وابسته به مقادیر درایه‌های آن است. به عنوان مثال اگر تعداد درایه‌های صفر یک سطر یا یک ستون زیاد باشد، بهتر است از آن سطر یا ستون برای بسط استفاده کنیم. مثلا در ماتریس زیر، بهتر است از ستون اول برای بسط استفاده کنیم:

\[ \beginvmatrix 1 & -1 & 8 \\ 0 & 3 & 1 \\ 0 & 2 & 1 \endvmatrix = (-1)^1+1 \times 1  \times \beginvmatrix 3 & 1 \\ 2 & 1 \endvmatrix + (-1)^2+1 \times 0  \times \beginvmatrix -1 & 8 \\ 2 & 1 \endvmatrix \] \[ + (-1)^3+1 \times 0 \times \beginvmatrix -1 & 8 \\ 3 & 1 \endvmatrix = 1 \times \Big( (-1)^1+1 \times 3 \times \vert 1 \vert + (-1)^2 + 1 \times 2 \times \vert 1 \vert \Big) + 0 + 0 = 1 \]

پیچیده‌گی زمانی بسط لاپلاس

همانطور که از تعریف مشخص است، در روش بسط لاپلاس، محاسبه‌ی دترمینان یک ماتریس مرتبه‌ی $n$ ، به محاسبه‌ی دترمینان $n$ ماتریس کهاد از مرتبه‌ی $n – 1$ شکسته می‌شود. اگر عمل اصلی محاسبات را اعمال ضرب و جمع در نظر گرفته و $T_1(n)$ تعداد این اعمال را برای محاسبه‌ی دترمینان ماتریس مرتبه‌ی $n$ به روش بسط لاپلاس نشان دهد، می‌توان نوشت:

\[ T_1( n ) = n T_1( n – 1 ) + n + n + n – 1 = n T_1( n – 1 ) + 3n – 1 \qquad, \qquad T_1( 1 ) = 0 \]

$ n T_1( n – 1) $: تعداد اعمال لازم برای محاسبه‌ی زیرمسائل

$n$: تعداد ضرب‌های بین $ a_ij $ و توان‌های زوج یا فرد منفی یک

$n$: تعداد ضرب‌های بین $ a_ij $ و $ det( A_ij)$

$n – 1$: تعداد جمع‌های لازم برای محاسبه‌ی نهایی

    حل این رابطه‌ی بازگشتی نشان می‌دهد $T_1(n)$ از مرتبه‌ی $O( n! ) $ است که برای $n$ های بزرگ کارایی ندارد.

روش گاوس برای محاسبه‌ی دترمینان ماتریس

برای محاسبه‌ی دترمینان یک ماتریس مربعی، خواصی وجود دارد که به اعمال مقدماتی سطری و ستونی مشهور بوده و عموما از روش بسط لاپلاس ثابت می‌شوند. تعدادی از این خواص به شرح زیر هستند:

    1- جابجا کردن دو سطر (یا دو ستون) ماتریس، مقدار دترمینان را قرینه می‌کند. در مثال زیر جای سطر اول و دوم عوض شده است:

\[ \beginvmatrix 1 & -1 & 8 \\ 3 & 3 & 1 \\ 7 & 2 & 1 \endvmatrix = – \beginvmatrix 3 & 3 & 1 \\ 1 & -1 & 8 \\ 7 & 2 & 1 \endvmatrix \]

    2- اگر تمام درایه‌های یک سطر (یا یک ستون) ماتریس در عددی مانند k ضرب شود، حاصل دترمینان نیز k برابر می‌شود. در مثال زیر سه برابر بودن درایه‌های متناظر سطر دوم ماتریس سمت چپ، نسبت به سطر دوم ماتریس سمت راست، مقدار دترمینان آن را نیز سه برابر کرده است:

\[ \beginvmatrix 1 & -1 & 8 \\ 3 & 3 & 6 \\ 7 & 2 & 1 \endvmatrix = 3 \times \beginvmatrix 1 & -1 & 8 \\ 1 & 1 & 2 \\ 7 & 2 & 1 \endvmatrix \]

    3- اگر ضریب ثابتی از درایه‌های یک سطر (یا یک ستون) ماتریس به سطر (یا ستون) دیگری اضافه شود، مقدار دترمینان تغییر نمی‌کند. در مثال زیر پنج برابر سطر اول به سطر سوم اضافه شده است:

\[ \beginvmatrix 1 & -1 & 8 \\ 3 & 3 & 6 \\ 7 & 2 & 1 \endvmatrix = \beginvmatrix 1 & -1 & 8 \\ 3 & 3 & 6 \\ 7 + 5 \times 1 & 2 + 5 \times (-1) & 1 + 5 \times 8 \endvmatrix \]

    4- دترمینان یک ماتریس مثلثی (ماتریسی که تمامی درایه‌های بالای قطر اصلی یا پایین قطر اصلی و یا هر دو صفر باشند) برابر حاصلضرب درایه‌های قطر اصلی آن است:

\[ \beginvmatrix 1 & -1 & 8 \\ 0 & 3 & 6 \\ 0 & 0 & 4 \endvmatrix = 1 \times 3 \times 4 = 12 \]

    5- ماتریسی که تمامی درایه‌های یک سطر (یا یک ستون) آن صفر باشد، دترمینان آن نیز صفر خواهد بود:

\[ \beginvmatrix 1 & -1 & 8 \\ 9 & 3 & 6 \\ 0 & 0 & 0 \endvmatrix = 0 \]

    در روش گاوس مراحل زیر انجام می‌شود:

    مرحله‌ی اول: اگر درایه‌ی سطر اول و ستون اول صفر است، سطری را که مقدار درایه‌ی ستون اول آن صفر نباشد به سطر اول منتقل می‌کنیم. این عمل مقدار دترمینان را تغییر علامت می‌دهد. اگر چنین سطری یافت نشد، یعنی تمامی درایه‌های ستون اول صفر هستند. پس بنا به خاصیت شماره‌ی پنج، مقدار دترمینان صفر شده و انجام مراحل بعدی نیاز نیست.

    مرحله‌ی دوم: ضریب مناسبی از مقدار درایه‌ی سطر اول و ستون اول را که درایه‌ی ستون اول هر سطر را صفر کند، به هر سطر به صورت مجزا اضافه  می‌کنیم. اگر مقدار درایه‌ی ستون اول آن ستون، از قبل صفر باشد، نیاز به انجام عمل خاصی نیست. این عمل مقدار دترمینان را تغییر نمی‌د‌هد.

    در مثال زیر، ستون اول سطر دوم مقدار صفر دارد. پس نیاز به انجام عملیات خاصی نیست. اما مقدار درایه‌ی ستون اول سطر سوم غیرصفر است. پس با اضافه کردن ضریب مناسبی از درایه‌های سطر اول به این سطر، مقدار آن را نیز صفر می‌کنیم. مقدار این ضریب با توجه به مقدار درایه‌ی سطر اول و ستون اول مشخص می‌شود که در این مثال منفی دو است:

\[ \beginvmatrix 1 & -1 & 8 \\ 0 & 3 & 1 \\ 2 & 1 & 1 \endvmatrix = \beginvmatrix 1 & -1 & 8 \\ 0 & 3 & 1 \\ 2 + (-2) \times 1 & 1 + (-2) \times (-1) & 1 + (-2) \times 8 \endvmatrix = \beginvmatrix 1 & -1 & 8 \\ 0 & 3 & 1 \\ 0 & 3 & -15 \endvmatrix \]

    مرحله‌ی سوم: در ماتریس به دست آمده، ستون اول آن، به غیر از سطر اول همه صفر هستد. بسط لاپلاس دترمینان ماتریس را بر اساس ستون اول انجام می‌دهیم:

\[ \beginvmatrix 1 & -1 & 8 \\ 0 & 3 & 1 \\ 0 & 3 & -15 \endvmatrix = (-1)^1+1 \times 1 \times \beginvmatrix 3 & 1 \\ 3 & -15 \endvmatrix = \beginvmatrix 3 & 1 \\ 3 & -15 \endvmatrix \]

    مرحله‌ی چهارم: محاسبه‌ی دترمینان ماتریس از مرتبه‌ی n به محاسبه‌ی دترمینان ماتریس مرتبه‌ی n – 1 تقلیل یافته است. با ادامه‌ی این مراحل برای این ماتریس، تا رسیدن به ماتریسی از مرتبه‌ی یک، مقدار دترمینان اصلی محاسبه می‌شود:

\[ \beginvmatrix 3 & 1 \\ 3 & -15 \endvmatrix = \beginvmatrix 3 & 1 \\ 3 + (-1) \times 3 & -15 + (-1) \times 1 \endvmatrix = \Big( (-1) ^ 1+1 \times 3 \times \vert -16 \vert  \Big) = -48 \]

    و در نتیجه:

\[ \beginvmatrix 1 & -1 & 8 \\ 0 & 3 & 1 \\ 2 & 1 & 1 \endvmatrix = -48 \]

پیچیده‌گی زمانی روش گاوس

اعمال ضرب و جمع را اعمال اصلی این روش در نظر گرفته و ( $ T_2( n ) $ را تعداد این اعمال برای محاسبه‌ی دترمینان به روش گاوس تعریف می‌کنیم. برای صفر کردن ستون اول هر سطر، ضریب مشخصی را محاسبه می کنیم که به یک عمل تقسیم (هم‌ارز ضرب) نیاز دارد. سپس حاصلضرب این ضریب در درایه‌های سطر اول را به درایه‌های متناظر آن سطر اضافه می‌کنیم. در نتیجه این مرحله برای هر سطر n عمل ضرب و $n$ عمل جمع دارد که برای $n – 1$ سطر باید اعمال شود. در پایان نیز با بسط لاپلاس روی ستون اول و یک عمل ضرب، به محاسبه‌ی دترمینان مرتبه‌ی $n – 1$ می‌رسیم. پس می‌توان نوشت:

\[ T_2(n) = 1 + (n-1)(n+n)  + T_2( n-1) + 1 = T_2 ( n-1) + 2n^2  – 2n + 2 \; \; , \; \; T_2(1) = 0 \]

    چنین رابطه‌ی بازگشتی‌ای از مرتبه‌ی $ O( n^ 3 ) $ است که بهبود چشمگیری در مقایسه با روش بسط لاپلاس با مرتبه‌ی $ O(n!) $ دارد.

    در واقع هدف از این الگوریتم، تبدیل ماتریس به یک ماتریس بالامثلثی (یا پایین‌مثلثی)، با استفاده از عملیات مقدماتی سطری و ستونی است. طبق خاصیت چهارم، مقدار دترمینان چنین ماتریسی برابر حاصلضرب درایه‌های قطر اصلی آن است:

\[ \beginvmatrix 1 & -1 & 8 \\ 0 & 3 & 1 \\ 2 & 1 & 1 \endvmatrix = \beginvmatrix 1 & -1 & 8 \\ 0 & 3 & 1 \\ 0 & 3 & -15 \endvmatrix = \beginvmatrix 1 & -1 & 8 \\ 0 & 3 & 1 \\ 0 & 0 & -16 \endvmatrix = 1 \times 3 \times -16 = -48 \]

    پیا��ه‌سازی این الگوریتم به سه حلقه‌ی تکرار تو در تو نیاز دارد که با یک حساب سرانگشتی مرتبه‌‌ی $O(n^3)$ را نشان می‌دهد.

    توجه: در برخی منابع این روش با عنوان گاوس-جردن معرفی می‌شود.

روش تحویل برای محاسبه‌ی دترمینان ماتریس

در بخش ضمیمه‌ی کتاب «حساب دیفرانسیل و انتگرال و هندسه تحلیلی» نوشته‌ی «جرج بی. توماس» و «راس ال. فینی»، فرمول تحویل از مقاله‌ی میلر به صورت زیر بیان شده است:

\[ \vert A \vert = \Big( \frac1a_11 \Big)^n-2 \beginvmatrix \beginvmatrix a_11 & a_12 \\ a_21 & a_22 \endvmatrix & \beginvmatrix a_11 & a_13 \\ a_21 & a_23 \endvmatrix & \cdots & \beginvmatrix a_11 & a_1n \\ a_21 & a_2n \endvmatrix \\ \beginvmatrix a_11 & a_12 \\ a_31 & a_32 \endvmatrix & \beginvmatrix a_11 & a_13 \\ a_31 & a_33 \endvmatrix & \cdots & \beginvmatrix a_11 & a_1n \\ a_31 & a_3n \endvmatrix \\ \vdots & \vdots & \ddots & \vdots \\ \beginvmatrix a_11 & a_12 \\ a_n1 & a_n2 \endvmatrix & \beginvmatrix a_11 & a_13 \\ a_n1 & a_n3 \endvmatrix & \cdots & \beginvmatrix a_11 & a_1n \\ a_n1 & a_nn \endvmatrix \endvmatrix \]

    یا به عبارت دیگر:

\[ \vert A \vert = \Big( \frac1a_11 \Big)^n-2 \beginvmatrix c_11 & c_12 & \cdots & c_1(n-1) \\ c_21 & c_22 & \cdots & c_2(n-1) \\ \vdots & \vdots & \ddots & \vdots \\ c_(n-1)1 & c_(n-1)2 & \cdots & c_(n-1)(n-1) \endvmatrix \; , \; c_ij = \beginvmatrix a_11 & a_i(j+1) \\ a_(i+1)1 & a_(i+1)(j+1) \endvmatrix \]

    به عنوان مثال:

\[ \beginvmatrix 2 & 4 & 1 & 1 \\ 0 & 2 & 1 & -1 \\ -2 & 1 & 2 & 0 \\ -1 & 1 & 0 & 3 \endvmatrix = \Big( \frac12 \Big)^4-2 \beginvmatrix \beginvmatrix 2 & 4 \\ 0 & 2 \endvmatrix & \beginvmatrix 2 & 1 \\ 0 & 1 \endvmatrix & \beginvmatrix 2 & 1 \\ 0 & -1 \endvmatrix \\ \beginvmatrix 2 & 4 \\ -2 & 1 \endvmatrix & \beginvmatrix 2 & 1 \\ -2 & 2 \endvmatrix & \beginvmatrix 2 & 1 \\ -2 & 0 \endvmatrix \\ \beginvmatrix 2 & 4 \\ -1 & 1 \endvmatrix & \beginvmatrix 2 & 1 \\ -1 & 0 \endvmatrix & \beginvmatrix 2 & 1 \\ -1 & 3 \endvmatrix \endvmatrix \] \[ = \Big( \frac12 \Big)^2 \beginvmatrix 4 & 2 & -2 \\ 10 & 6 & 2 \\ 6 & 1 & 7 \endvmatrix = \Big( \frac12 \Big)^2 \Big( \frac14 \Big)^3-2 \beginvmatrix 4 & 28 \\ -8 & 40 \endvmatrix = \frac14 \times \frac14 \times (160+224) = 24 \]

    واضح است که برای چنین محاسبه‌ای باید $a_11$ غیر صفر باشد. اگر اینچنین نبود، طبق اعمال مقدماتی سطر و ستون باید با جابجایی سطرها مقدار آن را غیر صفر کرد.

    این فرمول، مسأله از مرتبه‌ی $n$ را به یک زیرمسأله از مرتبه‌ی $n – 1$ ، و $ ( n – 1 )^2 $ زیرمسأله از مرتبه‌ی ۲ تبدیل می‌کند.

پیچیده‌گی زمانی فرمول تحویل

اگر $ T_3( n ) $ تعداد اعمال ضرب و جمع برای محاسبه به این روش باشد، می‌توان نوشت:

\[ T_3(n)=n-1+ T_3(n-1)+(n-1)^2 T_3(2) = T_3(n-1)+3n^2-5n+2 \;, \; T_3(2) = 3 \]

$n – 1$: تعداد تقسیم و ضرب‌های (یک تقسیم و $n – 2$ ضرب) لازم برای محاسبه‌ی توان $(n- 2)$ ام معکوس $ a_11 $ و ضرب آن در دترمینان

$T_3( n – 1 ) $: تعداد اعمال لازم برای حل زیرمسأله

$( n – 1 )^2 T_3( 2 )$: تعداد اعمال لازم برای محاسبه‌ی درایه‌های ماتریس زیرمسأله

    حل این رابطه‌ی بازگشتی نیز مرتبه‌ی پیچیده‌گی $ O(n^3) $ را نشان می‌دهد.

مقایسه‌ی روش‌های سه‌گانه

عملکرد سه روش بررسی شده را می‌توان اینگونه خلاصه کرد که:

    1- محاسبه‌ی پیچیده‌گی زمانی روش‌های سه‌گانه فوق نشان می‌دهد، کارآیی زمانی دو روش گاوس و فرمول تحویل تقریبا یکسان بوده و بسیار بهتر از روش بسط لاپلاس هستند.

    2- فضای مصرفی هر سه روش در صورت پیاده‌سازی بهینه‌ی آنها، همان فضای لازم برای ذخیره‌ی یک ماتریس مربعی از مرتبه‌ی $n$ است.

    3- هر سه روش ظاهری بازگشتی، با روش تقسیم و غلبه، دارند که حل مسأله از مرتبه‌ی $n$ را به حل زیرمسأله یا زیرمسائلی از مرتبه‌ی $n – 1$ تقسیم می‌کنند. اما پیاده‌سازی غیربازگشتی این روش‌ها نیز ممکن است که در روش گاوس توضیح مختصری داده شد.

    4- بر اساس روش بسط لاپلاس و با استفاده از استقرای ریاضی، می‌توان ثابت کرد که اگر تمامی درایه‌های یک ماتریس مربعی اعداد صحیح باشند، دترمینان آن نیز عدد صحیح خواهد بود. روش بسط لاپلاس صحیح بودن عدد دترمینان را در این شرایط تضمین می‌کند. چرا که تنها از اعمال جمع و ضرب تشکیل شده است که صحیح بودن عدد را تغییر نمی‌دهند. اما دو روش دیگر، با توجه به این که شامل عمل تقسیم نیز هستند، در زمان پیاده‌سازی ممکن است خطای محاسباتی ایجاد کنند. چرا که اکثر زبان‌های برنامه‌نویسی اعداد را به دو فرم صحیح یا اعشاری، با دقت مشخص، ذخیره می‌کنند. بنابراین اعداد گویای غیرصحیح به صورت تقریبی ذخیره شده و در محاسبات هم به همان صورت تقریبی به کار می‌روند.

    دترمینان ماتریس $A$ را که توسط بسط لاپلاس محاسبه کردیم، با استفاده از روش گاوس و با فرض ذخیره اعداد گویا به صورت اعشاری، با دقت شش رقم، مجددا محاسبه می‌کنیم:

\[ \beginvmatrix 1 & -1 & 8 \\ 0 & 3 & 1 \\ 2 & 2 & 1 \endvmatrix = \beginvmatrix 1 & -1 & 8 \\ 0 & 3 & 1 \\ 2 + (-2) \times 1 & 2 + (-2) \times (-1) & 1 + (-2) \times 8 \endvmatrix = \] \[ \beginvmatrix 1 & -1 & 8 \\ 0 & 3 & 1 \\ 0 & 4 & -15 \endvmatrix = \beginvmatrix 1 & -1 & 8 \\ 0 & 3 & 1 \\ 0 & 4 + (-1.333333) \times 3 & -15 + (-1.333333) \times 1 \endvmatrix \] \[ = \beginvmatrix 1 & -1 & 8 \\ 0 &∓ ۳ & 1 \\ 0 & 0 & -16.333333 \endvmatrix = -48.999999 \]

    این مسأله زمانی اهمیت دارد که محاسبه‌ی دقیق مد نظر بوده و امکان انجام عملیات حسابی روی اعداد گویا وجود نداشته باشد.

روش ساروس

دترمینان ماتریس سه در سه با استفاده از بسط لاپلاس به این ترتیب محاسبه می‌شود:

\[ \beginvmatrix a_11 & a_12 & a_13 \\ a_21 & a_22 & a_23 \\ a_31 & a_32 & a_33 \endvmatrix \] \[ = (-1)^1+1a_11 \beginvmatrix a_22 & a_23 \\ a_32 & a_33 \endvmatrix + (-1)^1+2a_12 \beginvmatrix a_21 & a_23 \\ a_31 & a_33 \endvmatrix + (-1)^1+3a_13 \beginvmatrix a_21 &∓ a_22 \\ a_31 & a_32 \endvmatrix \] \[ = a_11 (a_22 a_33-a_23a_32 ) – a_12 (a_21 a_33-a_23a_31 ) + a_13 (a_21 a_32-a_22a_31 ) \] \[ = a_11 a_22 a_33 + a_12 a_23 a_31 + a_13 a_21 a_32 – a_11 a_23 a_32 – a_12 a_21 a_33 – a_13 a_22 a_31 \]

[sanaye20-blog]

تحلیل رابطه خاکستری فازی (fuzzy GRA)

مفاهیم فازی

در مسائل تصمیم گیری، ما اغلب با موقعیت های غیرقطعی، فقدان اطلاعات دقیق، و ارزیابی های زبان شناختی ارائه شده بوسیله كارشناسان مواجه میشویم. در بسیاری موارد، اجبار تصمیم گیرندگان به ارائه ارزیابی عددی با استفاده از تصورات ذهنیشان غیرمنطقی است و واقع بینانه تر آن است كه تصمیم گیرندگان با ابزاری از اصطلاحات زبان شناختی برای معرفی مقادیر رتبه بندی و اهمیت نسبی معیارهای مورد نظر مجهز گردند. به منظور فائق آمدن بر این مشكلات، تئوری مجموعه فازی برای مقابله با گزاره های زبان طبیعی و ماهیت غیرقطعی اطلاعات مورد استفاده قرار گرفت. در زندگی روزمره، كلماتی وجود دارند كه اغلب برای توصیف متغیرها استفاده میشوند. به عنوان مثال هنگامی كه میگوییم" امروز گرم است " یا معادل آن " دمای هوای امروز بالا است". ما از واژه " بالا "برای توصیف"دمای هوای امروز" استفاده كردیم. بدین معنی كه متغیر دمای هوای امروز، واژه بالا را به عنوان مقدار خود پذیرفته است. واضح است كه متغیر دمای هوای امروز میتواند مقادیر نظیر 25 درجه سانتیگراد، 19 درجه سانتیگراد و ... را اختیار كند. هنگامیكه یك متغیر، اعداد را به عنوان مقدار بپذیرد، ما یك چهارچوب ریاضی مشخص برای فرموله كردن آن را داریم. ولی هنگامی كه متغیر، واژه ها را به عنوان مقدار میگیرد، در آن صورت چهارچوب مشخص برای فرموله كردن آن در تئوری كلاسیك نداریم، برای اینكه چنین چهارچوبی بدست آوریم، مفهوم متغیرهای زبانی مطرح شده است. به عبارتی متغیرهای زبانی به متغیرهایی گفته میشود كه مقادیر مورد قبول برای آنها به جای اعداد، كلمات و جملات زبانهای انسانی یا ماشینی هستند. همانگونه كه در محاسبات ریاضی از متغیرهای عددی استفاده میگردد، در منطق فازی نیز از متغیرهایزبانی (گفتاری یا غیر عددی) استفاده میگردد. متغیرهای زبانی بر اساس ارزشهایزبانی (گفتاری) كه در مجموعه عبارت (كلمات/ اصطلاحات) قرار دارند بیان می شود.

تحلیل رابطه خاکستری فازی

روش های تصمیم گیری چند معیاره (MCDM) از فنون پر کاربرد مدیریت و مهندسی صنایع هستند که به دو بخش تصمیم گیری چند شاخصه و تصمیم گیری چند هدفه تقسیم می شوند. تحلیل رابطه خاکستری در زمره روشهای تصمیم گیری چند شاخصه قرار دارد. هدف این روش رتبه بندی آلترناتیو های پژوهش است. در این تکنیک فرض بر این است که در مساله پژوهش تعدادی شاخص از نوع مثبت، منفی وجود دارند که اهمیت این شاخص ها نیز توسط خبرگان و یا روشهای دیگر محاسبه شده است همچنین در طرف دیگر مساله تعدادی گزینه وجود دارد که قرار است با در نظر گرفتن این شاخص ها رتبه بندی شوند. پیاده سازی این تکنیک در محیط فازی باعث دقت در نتایج و حذف عدم قطعیت های مساله تصمیم گیری می شود. در ادامه گام های این روش آورده شده است. 1- ایجاد ماتریس تصمیم فازی اولین گام تشکیل ماتریس تصمیم فازی است در ماتریس تصمیم، معیارها در ستون و گزینه ها در سطر قرار می گیرند و هر سلول امتیاز هر گزینه نسبت به هر معیار است. این ماتریس تصمیم با استفاده از طیف زیر تکمیل می شود این طیف 5 تایی فازی است که از عدد فازی 1و1و3 شروع و تا 7و9و11 خاتمه پیدا می کند. همچنین عبارات کلامی خیلی ضعیف (خیلی کم) تا خیلی خوب (خیلی زیاد) را شامل می شود. در این گام چنانچه از نظرات چند خبره استفاده شود، جهت ادغام از روش میانگین حسابی استفاده می شود.

2- نرمال سازی ماتریس تصمیم نرمال سازی در این روش همانند نرمال سازی روش تاپسیس فازی است. که از رابطه زیر استفاده می شود که چنانچه معیار جنبه مثبت داشته باشد از رابطه اول و چنانچه جنبه منفی داشته باشد از رابطه دوم استفاده می شود.

3- تعیین سری مرجع و فاصله گزینه ها تا آن در این بخش با استفاده از رابطه زیر سری مرجع را برای هر معیار محاسبه می کنیم سری مرجع برابر با بزرگترین درایه هر ستون معیار در نظر گرفته می شود. سپس فاصله هر گزینه تا آن سری مرجع d(A,B) برابر با فاصله اقلیدسی دو عدد فازی است.

4- تعیین ضریب رابطه خاکستری ضریب رابطه خاکستری از رابطه زیر بدست می آید در این رابطه r ضریب حل و فصل است و مقادیری بین صفر و 1 اختیار می کند و معمولا در پژوهش ها مقادیر 0.5 می گیرد.

5- امتیاز نهایی گزینه ها امتیاز نهایی گزینه ها از رابطه زیر بدست می آید در این رابطه W وزن معیارها است که باید با استفاده از روش های دیگر نظیر روش AHP فازی محاسبه شود و وارد این گام شود.

چنانچه نیازمند مشاوره و یا انجام پروژه خود با این روشها هستید با ما تماس بگیرید| 09338859181

Read the full article

[muzicnews]

دانلود آهنگ یاس بنام همه چیز درست میشه

آهنگ جدید یاس بنام همه چیز درست میشه

امروز با آهنگ زیبای ( همه چیز درست میشه ) از رسانه تاریخ ما در خدمت شما عزیزان هستیم

Download Music Of Singer : YAS From Tarikhema Media songs

دانلود آهنگ های یاس با لینک مستقیم و با کیفیت بالا از سایت آهنگ های تاریخ ما

——

جهت ورود به اینستاگرام این خواننده کلیک کنید

——-

متن آهنگ یاس بنام همه چیز درست میشه از یاس

——-

یه کلیشه ی جدید

همه چیز درست میشه یا همه چیز را درست می کنیم

به امید اینکه / همه چی مثل قبل خوب و خوب میشه و

غما دور میشنو دلامون نزدیک تر از قبل بهم مثله قبل

خوبه خوب میشه و غما دور میشنو

دلامون نزدیک تر از قبل بهم مثله قبل

من که قبل دنیا اومدم به لطف خالق

بدونه تجربه شدم تو نطفه بالغ

تمومه نامردیارو دونه دونه یادمه

وقتی بهترین عطر بویه خونه آدمه

قانون میگه بی رحمیو مرسوم بدونم

بعد باز پاکو معصوم بمونم

این یه حرفه حقه یا یه طنزه تلخه

از یه مغزه بسته که فکر نفعو نفته

ستمکارا فقط به غارت بردنو

ستم دیده ها تویه حقارت مردن

و تیکه هایه تو رو با شوق میبرن

با نهایت میل با قاشق میخورن

ولی چرا تو آرزو رو تویه سینه کشتی

فکرت اینه که تو همیشه زین به پشتی

خدا دیر گیره ولی شیر گیره

یه روزی ام سر ستم به زیر تیغ میره

همه چی مثله قبل خوبه خوب میشه و

غما دور میشنو دلامون نزدیک تر از قبل بهم مثله قبل

خوبه خوب میشه و غما دور میشنو

دلامون نزدیک تر از قبل بهم مثله قبل

از اینکه اینجا اوست کریم شاکرم

بهم حال کلی دادی میمونه تو خاطرم

هوامو داشته باش میشناسی یاسرم

خلاصه خیلی دمت گرم خیلی چاکرم

تو اون زمانی که من هستم در حال نوشت

انگار که رو به رویه درایه بهشتم

پس تو میکروفونو بردار بدش من

دور من یه دایره با پرگار بکش مرد

دلم میگه سکوته مرگبار رو بشکن اوجه موفقیته فرداتو عشقست

یه کارگر ساده یه سردار یه کشور

تو واسه خودتی منم یه سرباز که چشمم به فرداست

عشقم یه دریاست به کشور به فرداش تشنم به فریاد

حسمو حرفامو مصرعو ابیاتو حسم رو دریاب نبری اسمم رو از یاد هه

وقتی زیر بار فشار چشات خونه

وقتی بهت میگن اینو بچاپ نجات دوده

وقتی آرامشت خشاب خشاب قرصه

وقتی فقط دوروبرت بچاپ بچاپ دزده

وقتی دم خونت به امیده گنج در زدن

اونا که تو رو واسه خودت بخوان ۵ درصدن

وقتی طناب نجاتتو با عقده میبرن

تماشا میکنن میخندنو تخمه میخورن

وقتی بیکارا قاصبن و دیوارا کاذبن

و بیدارا کاسبنو بیزارا عازمن

تنها راه اینه که با دیدگاه تازه تر پیش بریم ما به پیشواز ساله بعد

همه چی مثله قبل خوبه خوب میشه و

غما دور میشنو دلامون نزدیک تر از قبل بهم مثله قبل

خوبه خوب میشه و غما دور میشنو

دلامون نزدیک تر از قبل بهم مثله قبل

تو این شرایطه بده نامرد اقتصادی که باید بسازی با درد افتضاحی

که اجتماعو کرده تبدیل به دشنه زاری که

باید پشته سرت دوتا چشم بذاری

ولی بکش بیرون از این فکر بیخودی

مشتی بس کن به مولا سکته میکنی

هه نشسته کشتیه خودم به گل

یکی باید همین حرفارو به خودم بگه

ولی مطئنم توام به آرزوت میرسی

حتی وقتی زندگی به تار موت میرسید

پنجره رو باز کن تا صدات به سقف آسمون برسه با من اینو داد بزن

همه چی مثله قبل خوبه خوب میشه و

غما دور میشنو دلامون نزدیک تر از قبل بهم مثله قبل

خوبه خوب میشه و غما دور میشنو

دلامون نزدیک تر از قبل بهم مثله قبل

—–|●♯♩♪♫♬♬♫♪♩♯●|—–

همه چیز درست میشه یاس

───┤ ♩♬♫♪♭ ├───

رسانه بزرگ آهنگهای تاریخ ما

───┤ ♩♬♫♪♭ ├───

نظرات و انقادات سازنده شما دلگرمی ماست و باعث پیشرفت رسانه خودتان میشود …

اگر این پست را پسندید لطفا به این پست 5 ستاره بدهید

نوشته دانلود آهنگ یاس بنام همه چیز درست میشه اولین بار در دانلود آهنگ. پدیدار شد.

source https://audio.tarikhema.org/%D8%B3%D8%A8%DA%A9-%D8%A2%D9%87%D9%86%DA%AF/rep/%D9%87%D9%85%D9%87-%DA%86%DB%8C%D8%B2-%D8%AF%D8%B1%D8%B3%D8%AA-%D9%85%DB%8C%D8%B4%D9%87-%DB%8C%D8%A7%D8%B3/

[mwahedbzhyblog-blog]

كۆ تا بریار له‌ لیژنه‌ی موه‌حید بژی سه‌باره‌ت به‌مامۆستا كامه‌ران سلامی الله تان لێ بیت به‌كۆی ده‌نگ له‌ینو خۆمان دا دوای كۆ بونه‌وه‌یه‌ك بڕیارمان دا كه‌ پۆست ڕابگرین له‌سه‌ر مامۆستا كامه‌ڕان كه‌ریم چونكه‌ به‌راستی نیهنیكی گه‌وره‌ له‌پشتێه‌وه‌یه‌تی ئێمه‌ گومانی خێر ده‌به‌ین به‌مامۆستا هه‌رچه‌نه‌ شێوه‌ی مردنه‌كه‌ی زۆر طه‌بیعی نییه‌ ئیمه‌ حسابی شێت بونی بۆ ئه‌كه‌ین چونكه‌ مامۆستایه‌كی صادق بوو كاری ناڕه‌وا له‌و ناوه‌شێته‌وه‌ ئه‌و ده‌رزی و ته‌عیزب نه‌فسی و گرتن و ئازارانه‌ی ئاسایشی هه‌وڵیر كه‌ ده‌رحه‌ق به‌مامۆستا ئه‌نجام یان دا كاری یه‌كه‌م جاریان نه‌بوو بوه‌ هۆكاری له‌ده‌ست دانی عه‌قڵ و هۆشی مامۆستا به‌راستی مامۆستا ته‌نها جه‌سه‌تی مابوو ئه‌گه‌رنا لایه‌نی رۆحی ومه‌عنه‌وی هیچ باش نه‌بوو تا ساڵیك دوای به‌ربونه‌كه���شی رۆژ به‌دوای رۆژ به‌رو خراپی ده‌رۆی چونكه‌ مفعولی ئه‌و حه‌پ و ده‌رمانانه‌ بوو كه‌ ده‌ی درایه‌ له‌بری ده‌رمانه‌كانی خۆی ماده‌ی هۆش به‌ری پی ده‌درا بۆ ئه‌وه‌ی مودمین بیت وه‌ دوای به‌ربونه‌كه‌ی توشی ده‌ست له‌رزین و قاچ له‌ریزن ببوو شیوازی قسه‌ كردنی دایم بێده‌نگی بوو خۆی له‌هیچ مه‌سائیلیك نه‌ده‌دا دائیمه‌ن ترسی هه‌بوو كه‌بێن بیگرنه‌وه‌ ده‌رسێكیان دابوه‌یه‌ له‌سجن دا شه‌وانه‌ و رۆژانه‌ دایم له‌به‌ر چاوی بوو خه‌وی نه‌بوو دایم بیری ئه‌كرده‌وه‌ وه‌نامانه‌وی ته‌فاسیل بده‌ینه‌ شیواز و كاره‌كان وه‌ شیوازی مردنه‌كه‌ی كه‌چۆن بوه‌و به‌چی مردوه‌ بۆ ئه‌وی نه‌بیته‌ فیتنه‌ بۆموه‌حیدان و تازه‌ موسڵمانان بڵین مامۆستایه‌كی وا به‌و شێوه‌ مرد به‌لام ئیمه‌ حسابی شیت بونی بۆ ئه‌كه‌ین و له‌ده‌ست دانی عه‌قڵی بۆ ئه‌نجام دانی ئه‌و كاره‌ی نحسبه شهیدا ان شاء الله ته‌واو داواش له‌و برایان و خوشكانه‌ ئه‌كه‌ین كه‌ ته‌واو باس و مه‌وزوعی مامۆستا ببڕینه‌وه‌ له‌لای خۆیان چونكه‌ ئه‌وان عیلمیان نییه‌ به‌شیواز و ژیانی و مردنی ئیمه‌ش له‌به‌ر ئه‌وه‌ی خانه‌واده‌ی توشی كیشه‌ی زیاتر نه‌بن له‌مه‌و دوا هیچ زانیاریه‌ك ناده‌ین له‌سه‌ری والسلام علیكم ورحمه‌ الله بابه‌ت : http://mwahed-bzhy.blogspot.com/2018/02/blog-post_7.html تیبنیی : مامۆستا تاجی سه‌رمانه‌ ئه‌م باسه‌ ئه‌كه‌ینه‌وه‌ بۆ ئه‌وه‌ی ئه‌گه‌ر سبه‌ینی هه‌ر هه‌واڵیكی ناخۆشتان بیست ئیوه‌ عوزر بهینه‌وه‌ وه‌ دواتر ئومیدی شه‌هید بونی بۆ بخوازن نه‌ك بلین شه‌هید بوه‌ و زۆر دوعای بۆ بكه‌ن چونكه‌ بوه‌ هۆی سه‌به‌بی هیدایه‌تی زۆر كه‌س الله ره‌حمی پی بكات و له‌گوناحی خۆش بێت وه‌ پاشان ئه‌وه‌شی كه‌ده‌ڵین شیت بوه‌ له‌به‌ر ئه‌وه‌ی كه‌ ده‌زگ

[bonian-n]

چرا شیعیان دوازده امامی، روایات فرقه هایی از شیعه را که همه امامان را قبول ندارند می پذیرند، اما روایات صحابه را قبول نمی کنند؟ از نظر علمای شیعه رد و قبول اخبار و احادیث دارای معیارهایی در راوی و در متن حدیث و… است، همچنین دارای روش های خاصی برای تمییز انواع مختلف روایات (صحیح، حسن، موثقه، ضعیف و…) است که از آن دو در علم رجال و درایه -به خصوص- بحث می شود. از مهم ترین و کلیدی ترین ... فوج https://fovj.ir http://ift.tt/2yHhfwZ

[xwendga]

اقیكردنه‌وه‌كانى (IELTS) لە هەرێمی کوردستان لە کاتی خۆیاندا ئەنجام دەدرێن و دوانەخراون

له‌ كۆبونه‌وه‌یه‌كدا لەگەڵ وه‌زاره‌تى خوێندنى باڵاو توێژینه‌وه‌ى زانستى دامەزراوەى بريتش كانسڵ(British Council) ئامادەیی نیشاندا بۆ فراوانکردن و زیادکردنی هەلی تاقیکردنەوەی (IELTS) لە سێنتەرەکانی هەرێمی کوردستان، هەروەک له‌باره‌ى ئه‌نجامدانى تاقیكردنه‌وه‌كانى نوانستى زمانى ئینگلیزى (IELTS) دڵنیایى درایه‌ سه‌رجه‌م كاندیدان و خوێندكاران، كه‌ تاقیكردنه‌وه‌كان له‌ سێنته‌ره‌كاندا له‌كات و ساتى دیارى كراوى خۆیدا به‌ڕێوه‌ده‌چێت و هیچ تاقیكردنه‌وه‌یه‌ك دواناخرێت.

عه‌باس ئه‌كره‌م وته‌بێژى وه‌زاره‌تى خوێندنى باڵاو توێژینه‌وه‌ى زانستى له‌ لێدوانێكدا ڕایگه‌یاند، دواى ئەوەى دەنگۆى ئەوە بڵاوکرایەوە کە بەهۆى ڕیفراندۆمى هەرێمى كوردستان تاقيكردنەوەکانى توانستى زمانى ئینگلیزى کێشەى بۆ دروستبوە، ڕۆژى چوارشەممە، ڕێکەوتى (١١/١٠/٢٠١٧) له‌دیوانى وه‌زاره‌تى خوێندنى باڵاو توێژینه‌وه‌ى زانستى كۆبونه‌وه‌یه‌ك له‌نێوان ستافی وەزارەت و نوێنه‌رى بریتش كانسڵ (British Council) بۆ تاوتوێكردنى تاقیكردنه‌وه‌كانى توانستى زمانى ئینگلیزى (IELTS) به‌ڕێوه‌چوو.

وته‌بێژى وه‌زاره‌تى خوێندنى باڵا ڕایگه‌یاند: لهو‌ كۆبونه‌وه‌كه‌دا ڕەتکرایەوە کەبەهۆى ریفراندۆمى هەرێمى کوردستان کێشە بۆ تاقیکردنەوەکانى (IELTS) دروست بووبێت و ئەو دەنگۆیانەش دورن لە ڕاستییەوە، هەروەک جه‌ختيش له‌سه‌ر ئه‌وه‌ كرایه‌وه‌ كە سه‌رجه‌م تاقیكردنه‌وه‌كانى (IELTS) له‌و كات و شوێنانه‌ى ده‌ستنیشان كراون وه‌ك خۆى به‌ڕێوه‌ده‌چێت و دڵنیایى كاندیدانى خوێندنى باڵا و خوێندكاران ده‌كه‌ین كه‌ هیچ واده‌یه‌كى تاقیكردنه‌وه‌كان دواناخراوە.

عه‌باس ئه‌كره‌م ڕاشیگه‌یاند هه‌ر له‌ كۆبونه‌وەکە‌دا بڕیاردرا کە ڕۆژى سێشه‌ممه‌ى داهاتوو كۆبونه‌وه‌یه‌كى دیکە له‌گه‌ڵ ستافى بریتش كانسڵ بەمەبەستی گفتوگۆکردن دەربارەی فراوانکردن و زیادکردنی هەلی تاقیکردنەوەی (IELTS) لە سێنتەرەکانی هەرێمی کوردستان به‌ڕێوه‌بچێت، لەم بارەیەوە دامەزراوەی (British Council) ئامادەیی خۆى نیشان داوە بۆ فروانکردنی زیاتری ئەم تاقیکردنەوەیە لە هەرێمی کوردستان.

[sanaye20-blog]

تکنیک تاپسیس (TOPSIS) توسعه یافته

مقدمه

روش تاپسیس (TOPSIS) از تکنیک های مشهور و پرطرفدار در ��صمیم گیری چند معیاره (MCDM) است به صورت دقیقتر بخواهیم بیان کنیم این تکنیک در زمره رویکرد تصمیم گیری چند شاخصه (MADM) است یعنی با هدف رتبه بندی چند گزینه با استفاده از تعدادی شاخص می باشد. در سالهای مختلف محققان زیادی بر روی روش تاپسیس فعالیت های مختلفی را انجام دادند از جمله ترکیب این روش با تکنیک های دیگر تصمیم گیری چند معیاره مانند ترکیب روش تاپسیس با روش AHP و یا پیاده سازی این روش در محیط های فازی و یا خاکستری. در مطالب پیشین به یک مدل از تکنیک های گسترش یافته شامل تاپسیس بهبود یافته پرداختیم که برای مطالعه می توانید وارد لینک روش تاپسیس بهبود یافته رجوع کنید. روش تاپسیس بهبود یافته با افزودن سه دو فاصله جدید به روش تاپسیس از جمله فاصله همینگ و فاصله خاکستری باعث بهبود نتایج روش تاپسیس شده است که به صورت مفصل به آن پرداخته شد. در این مطلب نیز حالت دیگری نیز از گسترش روش تاپسیس بنام تاپسیس توسعه یافته می پردازیم و گام های آن را ذکر خواهیم کرد.

گام های روش تاپسیس توسعه یافته

بر اساس مقاله Shih 2007 گام های توسعه یافته تاپسیس (topsis) به صورت زیر می باشد. نکته: این روش در مواقعی استفاده می شود که در مدل تاپسیس از نظر چند تصمیم گیرنده استفاده شود. در صورتی که داده های تاپسیس به صورت داده واقعی و کمی باشد و یا نظر یک تصمیم گیرنده اعمال شود از این تکنیک توان استفاده کرد و پیشنهاد می شود از روش تاپسیس سنتی و یا تاپسیس بهبود یافته استفاده شود. گام اول: تشکیل ماتریس تصمیم اولین گام در تمامی مدل های تصمیم کیری چند معیاره تشکیل ماتریس تصمیم است این ماتریس در روش تاپسیس به صورت یک ماتریس بیان می شود که از معیارها و گزینه های مساله تشکیل شده است این ماتریس تصمیم در اختیار چند خبره قرار داده می شود تا نظرات خود را در مورد امتیاز هر گزینه نسبت به هر معیار بر اساس طیف های مختلف کلامی بیان کنند. گام دوم: نرمال سازی ماتریس تصمیم در این گام ماتریس تصمیم هر پاسخ دهنده را بر اساس رابطه زیر نرمال می کنیم. در رابطه زیر xij در واقع ارزیابی گزینه i بر اساس معیار j است.

گام سوم: وزن دار کردن ماتریس نرمال در این گام باید وزن معیارها را در ماتریس نرمال ضرب کرد. این وزن معیارها باید توسط تکنیک های دیگر از جمله روش آنتروپی، روش فرایند تحلیل سلسله مراتبی AHP ، روش SWARA و ... محاسبه می شود و سپس وارد تاپسیس می شود آموزش تمامی این روشهای محاسبه وزن در این سایت آورده شده است. گام چهارم: تعیین ایده آل های مثبت (A+) و منفی (A-) در این گام بر اساس نوع معیارها ایده آل مثبت و منفی را بر اساس رابطه زیر مشخص می کنیم این رابطه بیان می کند چنانچه معیار جنبه سود داشته باشد ایده آل مثبت برابر با max درایه و ایده آل منفی برابر با min درایه است. و برای معیارهایی که جنبه هزینه دارند به صورت بالعکس.

گام پنجم: تعیین فاصله گزینه ها از ایده آل ها در این گام فاصله گزینه ها را از ایده آل ها مشخص می کنیم. که با استفاده از رابطه زیر انجام می گیرد. همانطور که ملاحظه می شود تمامی گام ها تا اینجا همانند روش تاپسیس سنتی است با این تفاوت که تک تک گام ها برای هر پاسخ دهنده باید صورت بگیرد.

گام ششم: ادغام فواصل گزینه ها در این گام با استفاده از رابطه زیر فواصل گزینه ها از ایده آل ها را که توسط هر پاسخ دهنده محاسبه شده است را ادغام می کنیم. در واقع این رابطه بیان می کند برای دستیابی به یک فاصله ادغام شده باید از فواصل بدست آمده از نظرات همه پاسخ دهندگان میانگین هندسی گرفته شود.

گام هفتم: محاسبه امتیاز هر گزینه در این گام با استفاده از رابطه زیر امتیاز هر گزینه را بدست می آوریم و بر اساس آن گرینه ها را رتبه بندی میکنیم. امتیاز هر گزینه عددی بین صفر و یک است و هرچقدر به یک نزدیکتر باشد نشان از برتر بودن گزینه دارد.

چنانچه نیازمند مشاوره و یا انجام پروژه خود با این روش هستید با ما تماس بگیرید| 09338859181

Read the full article

[sanaye20-blog]

روش تاپسیس بهبود یافته

مقدمه

در تمام دوران، تصمیم گیری صحیح همواره برگترین دغدغه جوامع بوده است. این تصمیم گیری گاه برای چند هدف که به آن تصمیم گیری چند هدفه (MODM) می گویند و گاه برای انتخاب یک گزینه بر اساس مجموعه ای است معیار که به آن تصمیم گیری چند شاخصه (MADM) می گویند کلیه این روش ها در مجموعه ای بزرگ بنام تصمیم گیری چند معیاره (MCDM) گرد هم آمده اند تا افراد بتوانند با استفاده از روش های علمی بهترین تصمیم را بگیرند. گاه این تصمیمات کوچک (خرید یک وسیله نقلیه و یا خرید یک لباس، شلوار و...) و گاه تصمیمات بزرگ (خرید خانه، انتخاب مکان کارخانه و...) است. یکی از این روشهایی که در این مطلب به آن خواهیم پرداخت روش تاپسیس بهبود یافته (Improve TOPSIS) است. در مطالب قبل روش تاپسیس (TOPSIS) را آموزش داده بودیم که در ادامه تفاوت آن را با روش تاپسیس بهبود یافته بررسی خواهیم کرد.

تاپسیس بهبود یافته (Improve TOPSIS)

این روش از تکنیک های جدید تصمیم گیری چند معیاره است که هدف آن رتبه بندی گزینه های پژوهش بر اساس مجموعه ای از معیارها است. این روش توسط آقای نیو (Niu) و همکاران در سال 2017 ارائه شد. در واقع این روش توسعه روش تاپسیس سنتی است زیرا نویسندگان این مقاله بیان داشتند که در روش تاپسیس سنتی محاسبه فاصله گزینه ها از ایده آل و ضد ایده آل توسط فاصله اقلیدسی محاسبه می شود که یک فاصله ابتدایی است بنابراین پیشنهاد دادند که دو فاصله همینگ و فاصله رابطه خاکستری (تحلیل رابطه خاکستری) به مدل تاپسیس سنتی اضافه شود و سپس این سه فاصله توسط رویکرد ضربی به یک فاصله نهایی تبدیل شوند و بر اساس آن ها روابط نهایی برای رتبه بندی گزینه ها صورت گیرد و بیان داشتند که  نتایج ارزیابی به دست آمده با استفاده از روش TOPSIS بهبود یافته است، کارآمد تر و متقاعد کننده تر است.

گام های تاپسیس بهبود یافته

1- تشکیل ماتریس تصمیم گام اول در این روش تشکیل ماتریس تصمیم است ماتریس تصمیم این روش همانند روشهای مشابه به صورت معیار گزینه ای است یعنی ماتریسیس که ستون ها معیارها و سطرها گزینه ها هستند. همچنین در این بخش نیز باید وزن معیارها از قبل محاسبه شده باید زیرا روش تاپسیس به تنهایی قادر به محاسبه وزن معیارها نیست برای محاسبه وزن معیارها روشهای زیادی وجود دارد که آموزش همگی در این سایت موجود است از جمله روش آنتروپی، AHP، بهترین بدترین (BWM) و SWARA. نمای کلی از ماتریس تصمیم در شکل زیر آورده شده است.

2- نرمال سازی ماتریس تصمیم جهت نرمال سازی ماتریس تصمیم از رابطه زیر استفاده می شود این رابطه بیان می کند که برای نرمال سازی باید هر درایه را بر جذرمجموع مربعات درایه های هر ستون معیار تقسیم کرد.

3- وزن دار کردن ماتریس تصمیم در این گام باید وزن معیارها که در ابتدا با استفاده از روشهای گفته شده محاسبه شده است را در ماتریس نرمال ضرب کرد تا ماتریس وزن دار حاصل شود. 4- تعیین ایده آل های مثبت و منفی در روش تاپسیس بهبود یافته، ایده آل های مثبت و منفی از رابطه زیر بدست می آیند. در واقع این رابطه بیان می کند که ایده آل مثبت برای معیارهای مثبت برابر با بزرگترین درایه ستون ماتریس موزون و ایده آل منفی کمترین مقدار ستون ماتریس موزن. برای معیارهای منفی نیز بالعکس.

5- محاسبه فاصله گزینه ها از ایده آل های مثبت و منفی در این گام فاصله گزینه ها را از ایده آل مثبت و منفی بر اساس سه فاصله اقلیدسی، همینگ و رابطه خاکستری بدست می آوریم. که به ترتیب این روابط در زیر آورده شده است. در واقع تفاوت تاپسیس بهبود یافته با روش تاپسیس سنتی در این گام خلاصه می شود.

  6- محاسبه درجه رویکرد ترکیبی در این گام با استفاده از رابطه زیر مقادیر نهایی فاصله گزینه ها از ایده آل مثبت (S+) و ایده آل منفی (S-) را با در نظر گرفتن هر سه فاصله محاسبه شده در گام قبل محاسبه می کنیم. در رابطه زیر u1 و u2 و u3 به ترتیب درجه اهمیت فواصل اقلیدسی، همینگ و تحلیل خاکستری است.

7- محاسبه ارزش کل و رتبه بندی گزینه ها در روش تاپسیس بهبود یافته ارزش کل هر گزینه از رابطه زیر بدست می آید در این رابطه مقدار Zi میزان ارزش کل هر گزینه هست که هرچقدر این ارزش عدد کمتری داشته باشد گزینه رتبه بهتری دارد.

جمع بندی

در این مطلب به آموزش روش تاپسیس بهبود یافته (Improve topsis) پرداخته شد و گام های آن بیان شد تفاوت این روش با تکنیک تاپسیس سنتی در محاسبه فواصل گزینه ها تا ایده آل مثبت و منفی بود که در روش بهبود یافته علاوه بر فاصله اقلیدسی، فاصله همینگ و رابطه خاکستری نیز اضافه شده است. در پایان مقاله ای که این روش را ارائه کرده بود با نتایج روش تاپسیس سنتی و چندین روش دیگر مقایساتی صورت گرفته بود که به این نتیجه رسیده بودند که جوابهای این روش اصولا دقت بالاتر و ��ابلیت اطمینان بیشتری دارند. چنانچه نیازمند مشاوره و یا انجام پروژه خود با این روش هستید با ما تماس بگیرید

Read the full article

[sanaye20-blog]

روش بولزای (وزن خاکستری سه پارامتره)

تکنیک بولزای (bull’s-eye) یکی از تکنیک های تصمیم گیری چند معیاره است که جهت محاسبه وزن در طیف اعداد خاکستری سه پارامتره است. که توسط دو محقق به نام های Lu & Wang (2012) ارائه شدکه جهت وزن دهی در ماتریس های تصمیم سه پارامتره به کار بردند که در ادامه در مورد آن بیشتر توضیح داده می شود.

تئوری خاکستری

تئوری سیستم های خاکستری اولین بار در سال 1982 توسط آقای دنگ ارائه شد که در ادامه توسط محققان دیگر توسعه داده شد. به این دلیل به آن خاکستری گفته می شود چون اگر ما حالت سفید را نشان از اطلاعات کاملا در دسترس و گویا در نظر بگیریم و سیاه به معنی اطلاعات کاملا ناشناخته باشد خاکستری حدی بین این دو است یعنی شامل اطلاعاتی است که تا حدی نامعلوم است شکل زیر نمایی از حالت خاکستری را بیان می کند که سیستم خاکستری نام دارد.

در واقع در سیستم خاکستری، وقتی صحبت از عدد خاکستری می شود عددی است که ارزش دقیق آن برای فرد مشخص نیست اما ناحیه ارزش آن مشخص است در سیستم خاکستری برای مشخص نمودن حدود ارزش از روش های آماری و یا توابع عضویت استفاده نمی شود بلکه مستقیم از داده های اصلی استفاده می شود. در واقع تفاوت مهم اعداد خاکستری و فازی در همین امر است که برای تعیین اعداد فازی باید توابع عضویت تعریف شود اما برای تشکیل اعداد خاکستری کافیست از نظر خبرگان کران های بالا و پایین استخراج شود.

اعداد خاکستری سه پارامتره

در صورتی که ⊗a یک عدد خاکستری سه پارامتره باشد این عدد به صورت زیر تعریف می شود که کران پایین همان کمترین مقداری است که برای آن تعریف می شود. مرکز ثقل یعنی عددی که بیشترین امکان را دارد. و کران بالا بیشترین مقدار عدد خاکستری است.

در صورتیکه مرکز ثقل عدد خاکستری سه متغیره مشخص نباشد تبدیل به عدد خاکستری عادی می شود که تنها دو حد پایین و بالا دارد. اگر ⊗b و ⊗a دو عدد خاکستری سه پارامتره باشند روابط جمع و تقسیم آن ها به صورت زیر می باشد.

همچنین فاصله بین دو عدد خاکستری به صورت d(⊗a,⊗b) نمایش داده می شود و از طریق رابطه زیر محاسبه می شود.

برای نرمال سازی اعداد خاکستری سه متغیره در ماتریس تصمیم به صورت زیر اقدام می کنیم. اگر ماتریس تصمیم گیری را بصورت زیر تعریف کنیم :

برای نرمال سازی چنانچه معیارها جنبه مثبت داشته باشند یعنی افزایش آن معیار ایجاد سود کند و مفید واقع شود از رابطه زیر استفاده می شود.

چنانچه معیار جنبه منفی داشته باشد یعنی کاهش آن باعث سود و بهبود در سیستم شود از رابطه زیر استفاده می شود.

روش وزن دهی بولزای

همانطور که پیش تر بیان شد روش بولزای جهت تعیین وزن در ماتریس های خاکستری سه پارامتره استفاده می شود این ماتریس به صورت معیار-گزینه است یعنی ستون های ماتریس معیارهای پژوهش هستند و سطرهای ماتریس گزینه های پژوهش را تشکیل می دهند هر سلول نیز ارزیابی هر گزینه بر اساس هر معیار است که می توان بر اساس یک عدد خاکستری سه تایی تکمیل کرد. در ادامه گام های این روش آورده شده است. گام اول: تشکیل ماتریس تصمیم طریقه محاسبه ماتریس تصمیم در بالا توضیح داده شد گام دوم: نرمال سازی ماتریس تصمیم جهت نرمال سازی از روابطی که در بالا اشاره شد برای نرمال کردن معیارهای مثبت و منفی استفاده می شود. گام سوم: تعیین بولزای مثبت برای تعیین بولزای مثبت از رابطه زیر استفاده می کنیم به بیان دیگر این رابطه بیان می کند که کافیست برای محاسبه بولزای مثبت ماکزیمم درایه های ستون معیار در ماتریس نرمال را استخراج کرد.

گام چهارم: محاسبه وزن تعدیل شده در این گام با استفاده از روابط زیر وزن تعدیل شده معیارها را محاسبه می کنیم. مقادیر α و β اهمیت وزن های بیرونی و درونی را مشخص می کنند و حاصل این دو برابر یک و هر دو غیر منفی هستند. این مقادیر معمولا توسط تصمیم گیرنده یا بر اساس نظر خبرگان تعیین می شود .

که در این رابطه bj برابر است با:

چنانچه نیازمند مشاوره رایگان و یا انجام پروژه خود با این روش هستید با ما تماس بگیرید| 09338859181

مطالب مرتبط و پیشنهادی: روش آنتروپی خاکستری (Grey Entropy) آموزش تحلیل رابطه خاکستری (GRA) Read the full article

[sanaye20-blog]

آموزش روش MAUT

تکنیک MAUT

روش MAUT (Multiple Attribute Utility Theory) بر تشکیل تابع مطلوبیت تصمیم گیرنده (DM) برای هر شاخص تاکید دارد و با ترکیب این توابع مطلوبیت، مطلوبیت هر گزینه را تعیین می کند. این تکنیک در سال 1982 وارد مدل های تصمیم گیری چند معیاره شد. هدف این روش رتبه بندی گزینه های پژوهش بر اساس معیارهای مساله است. مراحل پیاده سازی این تکنیک به صورت زیر است: گام 1: بهترین و بدترین مقادیر شاخص Xj را به ترتیب uh(j) و ul(j) می نامین بهترین مقدار یک شاخص مثبت، بیشترین مقدار آن و بدترین مقدار یک شاخص مثبت، کمترین مقدار آن است. در مورد شاخص های منفی، بهترین و بدترین مقدار به ترتیب برابر با کمترین و کمترین مقدار آن ها هستند. گام 2: برای هر شاخص، دستگاه 2 معادله و 2 مجهول زیر را تشکیل می دهیم. ul(j)αj+βj=0 uh(j)αj+βj=1 با توجه به اینکه مطلوبیت متناظر با ul را برابر با صفر و مطلوبیت متناظر با uh را برابر با 1 در نظر می گیریم، بنابراین جواب های دستگاه فوق نشان دهنده تابع مطلوبیت خطی شاخص Xj است. بدین صورت که αj برابر با شیب تابع مطلوبیت خطی وβj برابر با عرض از مبدا این تابع برای شاخصXj است. جواب دستگاه فوق همواره برابر است با:

گام 3: با داشتن مقادیر αj و βj تابع مطلوبیت خطی شاخص Xj که آن را با fj(aij) نمایش می دهیم با استفاده از رابطه زیر تعیین می شود.

گام 4: با جایگذاری ��قادیر ماتریس تصمیم (aij) در تابع مطلوبیت شاخص متناظر با آن، مطلوبیت گزینه ه�� به ازای شاخص ها به دست آمده و ماتریس مطلوبیت تشکیل داده می شود. uij=fj (aij) گام 5: مطلوبیت به دست آمده برای هر شاخص را در وزن آن شاخص ضرب می کنیم تا مطلوبیت های وزنی گزینه ها به ازای شاخص ها به دست آید. tij=uij × Wj گام 6: مجموع مطلوبیت های وزنی هر گزینه در کل شاخص ها برابر با مطلوبیت کل آن گزینه است. Ui=∑tij گام 7: رتبه بندی گزینه ها بر اساس مجموع مطلوبیت وزنی هر گزینه صورت می گیرد. هر گزینه مطلوبیت وزنی بیشتری داشته باشد رتبه بهتری دارد.

مثال روش MAUT

کارشناسان یک شرکت پیمانکار قصد دارند تا بهترین نوع اسکلت ساختمانی پروژه کنونی را تعیین کنند. بدین منظور 4 شاخص تعیین شده و انواع اسکلت مورد ارزیابی قرار گرفته که در جدول های زیر ملاحظه می شوند. تمامی شاخص ها از نوع خطی هستند با استفاده از تکنیک MAUT و تشکیل دستگاه معادلات خطی، بهترین نوع اسکلت ساختمانی را بیابید.

تمامی شاخص ها کمی هستند بنابراین نیازی به کمی سازی ماتریس تصمیم نداریم. گام 1: بهترین uh(j) و بدترین ul(j) مقدار هر شاخص را تعیین می کنیم.

گام 2: دستگاه های معادلات خطی را برای تمام شاخص ها تشکیل داده و مقادیر αj و βj را محاسبه می کنیم به عنوان مثال برای شاخص X3 داریم:

با استفاده از رابطه بالا که در گام دوم توضیحات اشاره شد مقادیر αj و βj به صورت زیر محاسبه می شوند.

به طریق مشابه مقادیر αj و βj برای تمامی شاخص ها محاسبه می شود که در جدول زیر آورده شده است.

گام 3: توابع مطلوبیت خطی را تعییم می کنیم که در زیر آورده شده است.

گام 4: مقادیر ماتریس تصمیم را در توابع به دست آمده جایگذاری می کنیم. به عنوان مثال:

به طریق مشابه برای تمامی درایه ها این محاسبات را انجام می دهیم که در جدول زیر آورده شده است.

گام 5: وزن معیارها را در ستون های ماتریس بالا ضرب می کنیم. این وزن معیارها از روشهای مختلفی محاسبه می شود از جمله می توان از روش AHP و یا روش آنتروپی شانون وزن معیارها را محاسبه نمود و وارد روش MAUT کرد.

گام 6: جمع سطری ماتریس به دست آمده در گام 5 برابر با مطلوبیت کل گزینه ها است. که در جدول زیر آورده شده است.

بنابراین گزینه A3 یعمی اسکلت کامپوزیت به عنوان بهترین گزینه انتخاب می شود. چنانچه نیازمند مشاوره و یا انجام پروژه خود با این روشها هستید با ما تماس بگیرید| 09338859181

Read the full article

[mthmtc]

حاصل ضرب تانسوری (۲- ضرب و پیچش)

پست جدید انتشار یافت https://mthmtcs.ir/tensor-product-2/

حاصل ضرب تانسوری (۲- ضرب و پیچش)

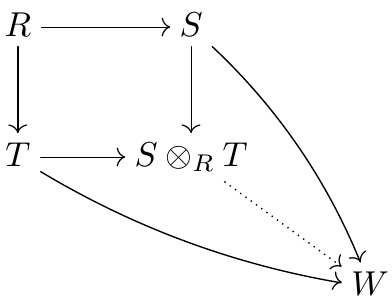
هنگاهی که $E$ و $F$ جبر می باشند می توان ضربی روی $E\odot F$ تعریف کرد با این خاصیت که برای هر $e_1, e_2\in E$ و $f_1, f_2\in F$ داریم $(e_1\otimes f_1)(e_2\otimes f_2):=e_1e_2\otimes f_1f_2$. برای تعریف چنین ضربی بصورت زیر عمل می کنیم. ابتدا برای هر $e\in E$ و $f\in F$ ثابت، نگاشت دوخطی $\psi_e,f:E\times F\To E\odot F$ تعریف شده بصورت $\psi_e,f:(g,h)\mapsto eg\otimes fh$ را در نظر می گیریم با استفاده از گزاره ۲٫۱ نگاشت خطی منحصر بفردی مانند $\varphi_e,f:E\odot F\To E\odot F$ وجود دارد بطوریکه $\varphi_e,f\circ\pi=\psi_e,f$. حال نگاشت دوخطی $\varphi:E\times F\To \rm Hom(E\odot F)$ را به صورت $\varphi:(e,f)\mapsto\varphi_e,f$ تعریف می کنیم دوباره با استفاده از گزاره ۲٫۱ نگاشت خطی منحصر بفردی مانند $\mu:E\odot F\To E\odot F$ وجود دارد بطوریکه $\mu\circ\pi=\varphi$ و \beginalign* \mu(\sum e_i\otimes f_i)(\sum g_j\otimes h_j)&=\sum\varphi(e_i,f_i)(\sum g_j\otimes h_j)\cr &=\sum\varphi_e_i,f_i(\sum g_j\otimes h_j)=\sum\sum e_ig_j\otimes f_ih_j \endalign* حال عمل ضرب بین دو عنصر $s,t\in E\odot F$ را $t\cdot s:=\mu(t)(s)$ تعریف می کنیم و $E\odot F$ تبدیل به یک جبر می شود. فضای برداری مزدوج، فضای برداری $V$ را با $V^c$ نمایش می دهیم. بنابراین $V$ با $V^c$ به عنوان گروه آبلی یکی هستند اما ضرب اسکالر روی $V^c$ به صورت $(\lambda,\upsilon)\mapsto\bar\lambda\upsilon$ تعریف می شود. اگر $V$ و $W$ فضاهای برداری مختلط باشند و $T:V\To W$ نگاشتی خطی و $S:V\To W$ نگاشتی مزدوج خطی باشد آنگاه نگاشتهای $T:V\To W^c$، $ T:V^c \To W $، $ S: V^c \To W^c $ خطی مزدوج و $T:V^c\To W^c$، $S:V\To W^c$، $S:V^c\To W$ خطی می باشند. اگر $E$ و $F$ $*$-جبر باشند می توان یک پیچش روی $E\odot F$ وابسته به پیچشهای که روی $E$ و $F$ وجود دارد، تعریف کرد. فرض کنیم $\frak s:E\times F\To (E\odot F)^c$ نگاشت دوخطی تعریف شده به صورت $\frak s:(e,f)\mapsto e^*\otimes f^*$ باشد بنابر گزاره ۲٫۱ نگاشت یکتای $*:E\odot F\To (E\odot F)^c$ بطوریکه $*\circ\pi=\frak s$. یعنی \beginalign* (\sum e_i\otimes f_i)^*=\sum e_i^*\otimes f_i^* \endalign*

گزاره ۵٫۱ : فرض کنید $B\:,\:A$ و $C$ جبر باشند. اگر $\psi:A\times B\To C$ نگاشت خطی ضربی ( یعنی $\psi(aa^\prime,bb^\prime)=\psi(a,b)\psi(a^\prime,b^\prime)$ ) باشد. آنگاه $\psi$ بطوریکتا به نگاشت خطی ضربی $\varphi:A\odot B\To C$ توسیع می یابد. اگر $\psi$ حافظ پیچش باشد، آنگاه $\varphi$ نیز چنین است.

اثبات: با استفاده از گزاره ۲٫۱ نگاشت خطی یکتای $\varphi:A\odot B\To C$ بطوریکه $\varphi\circ\pi=\psi$. لذا $\varphi(\sum a_i\otimes b_i)=\sum\psi(e_i,b_i)$. حال چون $\varphi$ خطی می باشد، کافی است ثابت کنیم \beginalign* \varphi((a_1\otimes b_1)(a_2\otimes b_2))&=\varphi(a_1a_2\otimes b_1b_2)\cr &=\psi(a_1a_2,b_1b_2)\cr &=\psi(a_1,b_1)\psi(a_2,b_2)\cr &=\varphi(a_1\otimes b_1)\varphi(a_2\otimes b_2) \endalign* لذا $\varphi$ ضربی می باشد. حال اگر $\psi$ حافظ پیچش باشد، دوباره با استفاده از خاصیت خطی $\varphi$ داریم $\varphi(a^*\otimes b^*)=\psi(a^*,b^*)=\psi(a,b)^*=\varphi(a\otimes b)^*$ و در نتیجه $\varphi$ حافظ پیچش می باشد. $\square$

با استفاده از گزاره های ۲٫۱ و ۵٫۱ نتایج مهم زیر را داریم

اگر $\psi_E:E\To G$ و $\psi_F:F\To H$ نگاشتهای خطی باشند، آنگاه $\psi_E\odot\psi_F:E\odot F\To G\odot H$ را نگاشت خطی تعریف شده به صورت $\psi_E\odot\psi_F:e\otimes f\mapsto \psi(e)\otimes\psi(f)$ در نظر می گیریم که توسیع نگاشت دوخطی $(e,f)\mapsto \psi(e)\otimes\psi(f)$ می باشد. اگر در فضاهای زمینه ضرب تعریف شده باشد و $\psi_E,\psi_F$ ضربی باشند آنگاه $\psi_E\odot\psi_F$ نیز ضربی خواهد بود.

اگر $\varphi_E:E\To G$ و $\varphi_F:F\To G$ نگاشتهای خطی و $G$ جبر باشد، آنگاه $\varphi_E\odot\varphi_F:E\odot F\To G$ را نگاشت تعریف شده به صورت $\varphi_E\odot\varphi_F:e\otimes f\mapsto \varphi_E(e)\,.\,\varphi_F(f)$ در نظر می گیریم که توسیع نگاشت دوخطی $(e,f)\mapsto \varphi_E(e)\,.\,\varphi_F(f)$ می باشد. اگر $E$ و $F$ جبر باشند و $\varphi_E,\varphi_F$ ضربی و جابجا (یعنی $\varphi_E(e)\varphi_F(f)=\varphi_F(f)\varphi_E(e)$) شوند، آنگاه $\varphi_E\odot\varphi_F$ نیز ضربی می باشند.

در مثالهای بالا با استفاده از نگاشتهای خطی روی فضاها، نگاشتهایی خطی روی ضرب تانسوری این فضاها تعریف کردیم. عکس این سوال نیز مهم است. یعنی آیا برای نگاشت $\xi:E\odot F\To G$، نگاشتهای $\varphi_E:E\To G$ و $\varphi_F:F\To G$ وجود دارد بطوریکه $\varphi_E\odot\varphi_F=\xi$. هنگامی که $\varphi_E$ و $\varphi_F$ وجود داشته باشند آنها را تحدید $\xi$ خوانیم.

مثال ۱٫۱ :

$A\simeq A\odot \Bbb C$ . فرض کنیم نگاشت خطی $\varphi:\sum a_k\otimes\lambda_k\mapsto \sum\lambda_k a_k$ از $A\odot\Bbb C$ بتوی $A$ توسیع نگاشت دوخطی $(a,\lambda)\mapsto \lambda a$ از $A\times\Bbb C$ به $A$ باشد. بوضوح $\varphi$ پوشا و یک به یک می باشد. اگر $A$ جبر (با پیچش) باشد آنگاه $\varphi$ ضربی (حافظ پیچش) می باشد.

جبرهای ماتریسی: $A\odot\Bbb M_n(\Bbb C)\simeq\Bbb M_n(A)$ ماتریسهای $n\times n$ با ۱ در درایه با سطر $i$ و ستون $j$ و بقیه درایه ها صفر. لذا هر عضو $A\odot \Bbb M_n$ را می توان بطور منحصر بفرد به صورت \beginalign* t=\sum a_i j\otimes e_i j \endalign* نوشت. حال نگاشت $\psi:A\odot\Bbb M_n(\Bbb C)\To \Bbb M_n(A)$ تعریف شده بصورت $\psi:\sum a_i j\otimes e_i j\mapsto (a_i j)$ خطی و ضربی ($e_i j\cdot e_km=\delta_j k\cdot e_i m$) و حافظ پیچش ($e_i j^*=e_j i$) می باشد و آشکارا دوسویی نیز می باشد.

نشاندن به عنوان زیرمجموعه چگال: $C_0(X)\odot A\hookrightarrow C_0(X\rightarrow A)$ که $X$ فضای موضعاً فشرده و $A$ $C^*$-جبر می باشد. فرض کنیم نگاشت خطی $\varphi:C_0(X)\odot A\To C_0(X\rightarrow A)$ توسیع نگاشت دوخطی $\psi:C_0(x)\times A\To C_0(X\rightarrow A)$ تعریف شده به صورت $\psi:(f,a)\mapsto \psi_(f,a)$ که $\psi_(f,a)(x)=f(x)a$ اشد. واضح است که $\psi_(f,a)\in C_0(X\rightarrow A)$. حال ثابت می کنیم که $\varphi$ یک به یک می باشد. فرض کنیم $\a_j\_J$ پایه ای برای $A$ باشد. پس می توان هر عضو $C_0(X)\odot $ را بطور یکتا به صورت $\sum f_j\otimes a_j$ نوشت. حال فرض کنیم $\varphi(\sum f_j\otimes a_j)=0$ لذا $\sum\psi_(f_j,a_j)=0$ و در نتیجه برای هر $x\in X$ داریم $\sum\psi_(f_j.a_j)(x)=\sum f_j(x)a_j=0$ و در نتیجه برای هر $x\in X$ و هر $j$ داریم $f_j(x)=0$ و $f_j\equiv 0$ پس $\sum f_j\otimes a_j=0$ و $\varphi$ یک به یک می باشد. حال نشان می دهیم که $C_0(X)\odot A$ در $C_0(X\rightarrow A)$ چگال می باشد. فرض کنیم $f\in C_0(X\rightarrow A)\ ,\ 0 \beginalign* \cal O_x:=\\ f_0(x)\ -\ f_0(y)\ \ \endalign* چون $X_0$ فشرده می باشد لذا این پوشش دارای زیر پوشش متناهی می باشد. پس $x_1,\ldots,x_n$ وجود دارد بطوریکه $X_0\subseteq\cup_i=1^n \cal O_x_i $ . با استفاده از قضیه افراز واحد ((گزاره ۴۱.۴ کتاب آنالیز حقیقی فولند)) روی $X_0$ داریم: توابع $g_x_i\in C_0(X\rightarrow [0,1])$ وجود دارد بطوریکه $g_x_i|X_0\backslash\cal O_x_i=0$ و $\sum g_x_i=1$ روی $X_0$ و $۰\leq\sum g_x_i\leq 1$ روی $X\backslash X_0$ . فرض کنیم $g:=\sum g_x_i\otimes f(x_i)$ پس $g\in C_0(X)\odot A$ و $\varphi(g)$ تقریبی از $f_0$ و لذا تقریبی از $f$ می باشد.

[sanaye20-blog]

آموزش روش الکتره فازی (fuzzy ELECTRE)

روش الکتره (ELECTRE) از روشهای پرکاربرد تصمیم گیری چند شاخصه است استفاده از روش الکتره فازی (fuzzy electre) با توجه به ماهیت عدم اطمینان و ابهام موجود در ارزيابی مقایسات جهت تکمیل ماتريسی عملکرد تصمیم گیری استفاده می شود. تکنیک ELECTRE از حروف اول عبارت Elimination et choice trancelating reality به معنی روش حذف و انتخاب سازگار با واقعیت می باشد البته بیشتر به نام روش تسلط تقریبی معروف است. این تکنیک در سال 1966 توسط ساسمن، روی و بنایون ارائه شد در این روش، گزینه های رقیب با استفاده از مقایسه های غیر رتبه ای ارزیابی می شوند.

گام های روش الکتره فازی

روش الکتره فازی در 10 گام انجام  می شود که در ادامه توضیح داده شده است:

گام اول: تشکیل ماتریس تصمیم فازی

برای تشکیل ماتریس تصمیم فازی از m گزینه و n معیار استفاده می شود، ابتدا اهمیت فازی هر معیار مشخص می شود این اهمیت همان وزن معیار است که می تواند مستقیم توسط تصمیم گیرنده تعیین شود و یا اینکه از روشهایی نظیر AHP فازی و یا BWM فازی تعیین شود. البته می توان وزنها را به صورت قطعی تعیین کرد و جهت فازی کردن آن وزن را سه بار تکرار نمود.

گام دوم: نرمال سازی ماتریس تصمیم

نرمال سازی در روش الکتره فازی (fuzzy electre) توسط دو رابطه زیر برای معیارهای مثبت و منفی انجام می شود اگر معیار جنبه مثبت داشته باشد یعنی افزایش آن معیار باعث بهبود در سیستم شود از رابطه اول استفاده میکنیم و اگر معیار جنبه منفی داشته باشد یعنی کاهش آن باعث بهبود در سیستم شود از رابطه دوم استفاده می شود.

گام سوم: تشکیل ماترس نرمال وزن دار

در این گام وزن های معیارها که در گام 1 بدست آورده بودیم را در ماتریس نرمال ضرب می کنیم. تا ماتریس وزن دار حاصل شود.

گام چهارم: محاسبه فاصله بین هر دو گزینه

در این گام با استفاده از رابطه زیر فاصله بین هر دو گزینه مساله را نسبت به هر معیار بدست می آوریم.

مجموعه هماهنگ و ناهمانگ از ماتریس وزن دار شده بدست می آیند و برای تشکیل ماتریس های هماهنگ و ناهماهنگ از رابطه بالا استفاده می شود.

گام پنجم: ساخت مجموعه موافق و ایجاد ماتریس موافقت

مجموعه موافق مجموعه ای از معیارهایی است که Vxj>Vyj است که V همان ماتریس نرمال وزن دار است. که ماتریس موافقت از مجموع وزن تمام معیارهای موجود در مجموعه موافق بر اساس رابطه زیر حاصل می شود.

سپس مقدار آستانه مجموعه موافق را از رابطه زیر بدست می آوریم. که این همان میانگین حسابی از درایه های ماتریس موافق است.

گام ششم: تشکیل ماتریس بولین موافق

با استفاده از مقدار آستانه و ماتریس موافق، می توان ماتریس بولین (صفر و یک) را ایجاد کرد. اگر درایه ماتریس موافق از مقدار آستانه بزرگتر باشد عدد متناظر آن در ماتریس بولین 1 می شود و در غیر اینصورت مقدار صفر اختیار می کند.

گام هفتم: ساخت مجموعه مخالف و ایجاد ماتریس مخالفت

مجموعه مخالف مجموعه ای از معیارهایی است که Vxj Read the full article

[xwendga]

وه‌زیری په‌روه‌رده‌ به‌ڵێنێك به‌مامۆستایان ده‌دات

وه‌زیری په‌روه‌رده‌ به‌ڵێنێك به‌مامۆستایان ده‌دات..ده‌رماڵه‌یه‌كیان پێده‌درێت یه‌كێتیی‌ مامۆستایان ڕونكردنه‌وه‌ له‌باره‌ی‌ ده‌رماڵه‌یه‌كی‌ تایبه‌ت به‌مامۆستایانی‌ سه‌رپه‌رشتیار ده‌دات و جێگری‌ سه‌رۆكی‌ یه‌كێتیه‌كه‌ش به‌ڵێنێكی‌ وه‌زیری په‌روه‌رده‌ له‌به‌رژه‌وه‌ندی ئه‌و مامۆستا سه‌رپه‌رشتیارانه‌ ئاشكراده‌كات. مامۆستا عه‌تا ئه‌حمه‌د جێگری‌ سه‌رۆكی‌ یه‌كێتی‌ مامۆستایان به‌SNNی‌ ڕاگه‌یاند، “دوێنێ وه‌ك ڕێكخراوی‌ یه‌كێتیی‌ مامۆستایان كۆبونه‌وه‌یه‌كمان له‌گه‌ڵ وه‌زیری په‌روه‌رده‌ ئه‌نجامدا كه‌ تیایدا تاوتوێی چه‌ند پرسێكی‌ په‌یوه‌ندیدار به‌مامۆستایان و خوێندكاران و سێكته‌ری‌ په‌روه‌رده‌ كرا”.

وتیشی:”له‌كۆبونه‌وه‌كه‌دا داوامان له‌وه‌زیری په‌روه‌رده‌ كرد ئه‌و ده‌رماڵه‌یه‌ی‌ پێشتر به‌بڕی‌ 150 هه‌زار دینار بۆ مامۆستایانی‌ سه‌رپه‌رشتیار خه‌رجده‌كرا، ئێستا چاره‌نوسی به‌كوێده‌گات، ئاخۆ ده‌رماڵه‌ی هاتوچۆ بۆ ئه‌و مامۆستایانه‌ خه‌رجده‌كرێت له‌كاتێكدا كه‌ له‌ده‌رماڵه‌ی‌ هاندانیش بێبه‌شكراون؟”.

مامۆستا عه‌تا وه‌ڵامی‌ وه‌زیری‌ په‌روه‌رده‌ی‌ ڕاگه‌یاند كه‌ وتویه‌تی‌ ((ئه‌و ده‌رماڵه‌یه‌ی‌ پێشتر به‌بڕی 150 هه‌زار دینار ده‌درایه‌ مامۆستایانی‌ سه‌رپه‌رشتیار بڕیاری‌ له‌باره‌وه‌دراوه‌و كه‌مكراوته‌وه‌ بۆ 75 هه‌زار دینارو بڕیاره‌ ئه‌و ده‌رماڵه‌یه‌ش له‌مانگی حوزیرانه‌وه‌ بۆ مامۆستایان خه‌رجبكرێت)).

به‌بۆچونی‌ جێگری‌ سه‌رۆكی‌ یه‌كێتیی‌ مامۆستایان، “تائێستا نازانرێت وه‌زاره‌تی‌ دارایی بڕیاری‌ خه‌رجكردنی‌ ئه‌و ده‌رماڵه‌یه‌ بۆ مامۆستایانی‌ سه‌رپه‌رشتیار جێبه‌جێده‌كات یاخود نا”.

ئه‌وه‌شی‌ وت:”خه‌رجكردنی‌ ئه‌و ده‌رماڵه‌یه‌ بۆ مامۆستایانی‌ سه‌رپه‌رشتیار ناخرێته‌سه‌ر موچه‌، به‌ڵكو به‌جیا ده‌درێته‌ ئه‌و مامۆستایانه‌ی ئه‌ركی‌ به‌سه‌ركردنه‌وه‌ی‌ خوێندنگه‌كانیان له‌ئه‌ستۆدابوه‌”.

  نووسراوه‌ له‌لایه‌ن Raw Raw

[xwendga]

پۆلی12 ه‌کان ئاگادار بن ڕه‌وێن گه‌ردی ئه‌مڕۆ له‌ وه‌زاره‌تی خوێندنی باڵا گرینگ ترین پرسیاری کرد گرینگ ترین وه‌ڵام درایه‌وه‌