fuckyeahmatlabart

[fuckyeahmatlabart]

I feel lied to. This is where the bugs bunny NO meme cokes from

[fuckyeahmatlabart]

This is an animation i made in Matlab of the shallow water equations with a closed boundary! The shallow water equations are a set of hyperbolic partial differential equations that describe the flow below a pressure surface in a fluid.

[fuckyeahmatlabart]

Hey there,

First of all, I’m a big fan of your blog! I’m an Engineering student who uses Matlab a lot for simulation and I combined my knowledge on the software with my passion for digital design. I have an Society6 account with some of the designs for sale (here).

Hope you guys like it!

[fuckyeahmatlabart]

It's not MATLAB, but still an awesome find that I wanted to share: donut.c.

This donut shaped code is courtesy of Andy Sloane, at a1k0n.net. Click here to see what the code does.

[fuckyeahmatlabart]

Help wanted!

Life keeps getting in the way of keeping this blog running. If anyone would be interested in becoming an admin and helping me out, please send me a message!

[fuckyeahmatlabart]

Periodic boundary conditions as the surface of a torus. Von Neumann boundary conditions as a quarter torus.

These are both exact invariant solutions to a set of nonlinear field equations related to cardiac dynamics with 73728 and 294912 degrees of freedom, respectively.

[fuckyeahmatlabart]

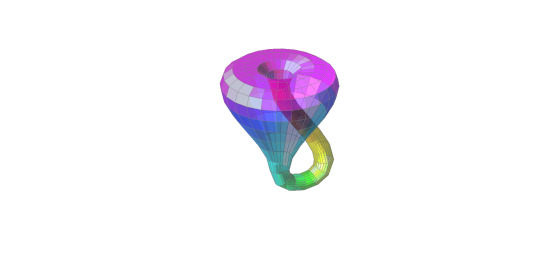
Generated a Klein Bottle using Matlab. This will probably sound weird to most people but I find them absolutely fascinating. They’re an example of a non-orientable, two-dimensional manifold meaning it is mathematically compact without boundaries. Notions of left and right can not be consistently defined.

[fuckyeahmatlabart]

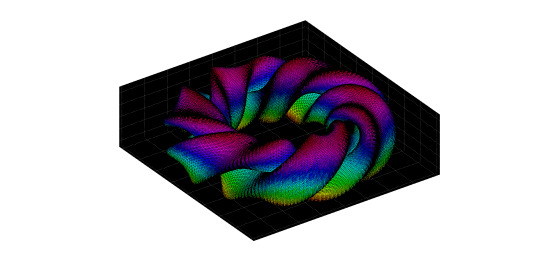
Well… I uh… generated this thing in matlab. I shall call it… what the hell should I even call this?

[fuckyeahmatlabart]

The Buddhabrot fractal. Representing the orbits of initial value C in the complex plane for which the sequence:   tends to infinity. This example uses 100 iterations, and has been processed in photoshop to boost highlights and blacks.

[fuckyeahmatlabart]

Yet another nonsense heat plane. 

[fuckyeahmatlabart]

ETDRK4 solution of the cubic nonlinear Schrödinger equation with periodic boundary conditions. This actually has an additional term proportional to a Gaussian of the magnitude of the (complex) field, but the difference is basically negligible, visually. The simulation reflects in time every \(\pi\), so here we only have the fundamental time-domain.

[fuckyeahmatlabart]

Snow equation, closely related to the Kuramoto-Sivashinsky equation, which apparently attempts to model the formation of snow patterns under melting from the sun. Pretty cool. It actually does look like sun cup patterns when solved in two spatial dimensions.

[fuckyeahmatlabart]

Chevons 2.

[fuckyeahmatlabart]

After finishing Breaking Bad, I couldn’t help it

[fuckyeahmatlabart]

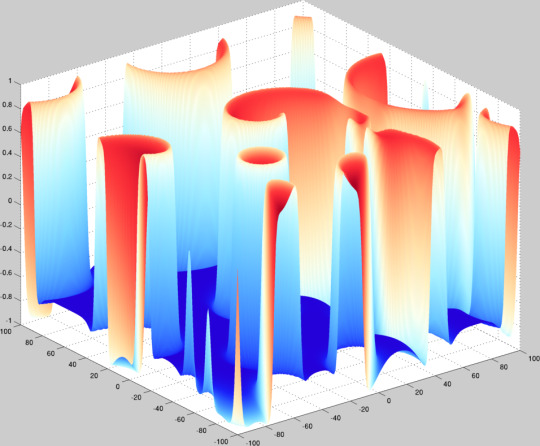
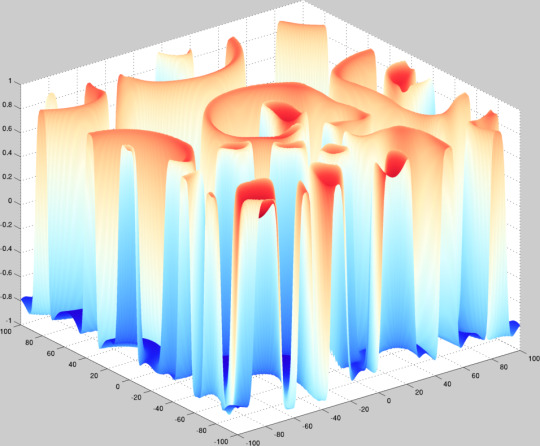
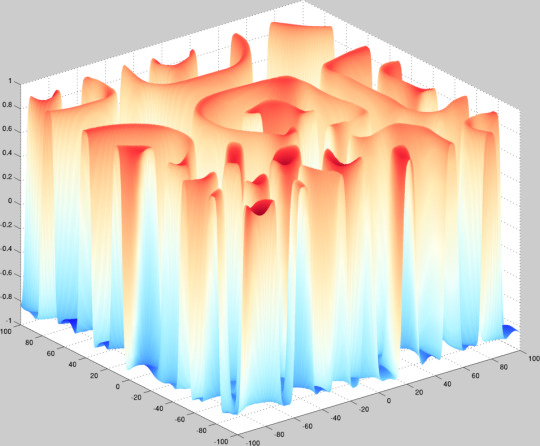
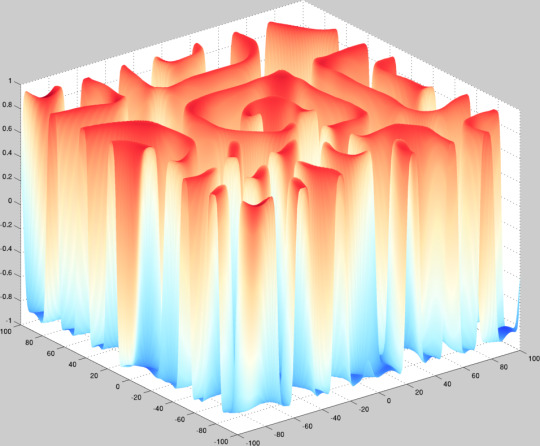
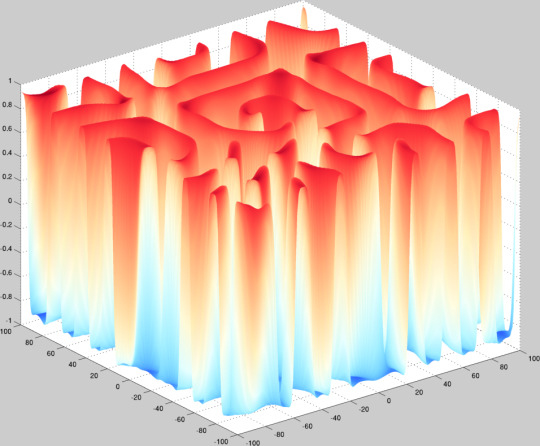
Fitzhugh-Nagumo system taken from a parameter region which forms stable spirals to a region which forms a steady-state labyrinthine structure. Pattern formation is cool.

\[ u_t = \Delta u + u - v - u^{3} \] \[ v_t = \delta\Delta v + \epsilon(u - a_{1}v - a_{0}) \]

The plot height is given by the \(u\) variable and the color by the \(v\) variable. I just used a uniform mesh for the parameter continuation and clearly should have done some sort of arc-length or sequential difference norm allocation because, as is, we go from spirals to labyrinths immediately and stay there and that’s not very interesting.

[fuckyeahmatlabart]

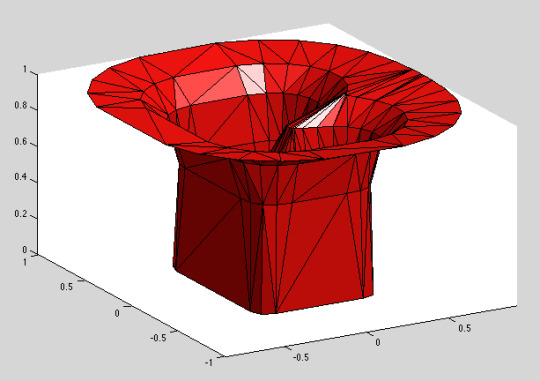
I sped up the curve erosion code by about 24x this morning. (Your mileage may vary. The algorithm is still a pokey n^2, but n is small.) Then I bundled the triangulation algorithm into a nice function and got it all set up so I can write better code.

By changing the erosion parameters I can flare the hole the way I want it. Almost ready to use! xy0 = cornerRoundingSpline(x, y, 0.1, 3); xy1 = cornerRoundingSpline(x, y, 0.2, 5); xy2 = erode(xy1, 0.1, 0.01); xy3 = erode(xy2, 0.2, 0.01); xy4 = erode(xy3, 0.4, 0.01); [v f] = triangulateSides({appendZ(xy0, 0), ... appendZ(xy1, 0.6), ... appendZ(xy2, 0.84), ... appendZ(xy3, 0.96), ... appendZ(xy4, 1)});

[fuckyeahmatlabart]

Go Home, Netflix…

Watching “Bones” on Melissa’s laptop, and Netflix started freaking out. Grabbed a few frames, here’s a scan over several of them (flipping between each frame) that I made with Matlab.