This blog showcases the skills I have developed related to data science and analytics
Don't wanna be here? Send us removal request.
Text
Some of the plots are below
#Q-Q plot for normality fig4=sm.qqplot(results2.resid, line='r')
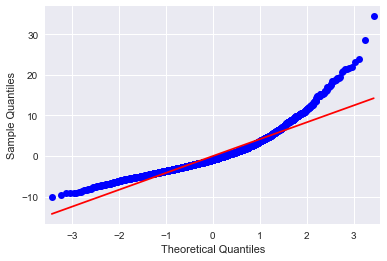
# simple plot of residuals stdres=pandas.DataFrame(results2.resid_pearson) plt.plot(stdres, 'o', ls='None') l = plt.axhline(y=0, color='r') plt.ylabel('Standardized Residual') plt.xlabel('Observation Number')
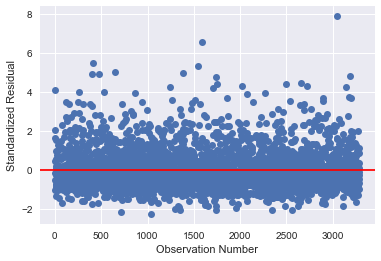
# additional regression diagnostic plots fig2 = plt.figure() fig2 = sm.graphics.plot_regress_exog(results2, "H1DA8", fig=fig2)

Regression Modelling Week 3 Assignment- Multiple Regression-Confounding variables
The data that I used for multiple regression is addhealth data. Below are the decriptions of the vraibales used in the analysis.
“H1DA5”= Sport hours
H1GH59A"= Height part in foot
H1GH59B"= Height part in inches
“H1DA8”= TV hours
Below I am importing the stats models and reading the data
import pandas import numpy import statsmodels.formula.api as smf import statsmodels.stats.multicomp as multi
data = pandas.read_csv(‘addhealth.csv’, low_memory=False)
Descriptive statistics for number of hours active in sports per week. In [25]:
data["H1DA5"].describe()
Out[25]:
count 6504.000000 mean 1.386839 std 1.158692 min 0.000000 25% 0.000000 50% 1.000000 75% 2.000000 max 8.000000 Name: H1DA5, dtype: float64
In [26]:
data["H1DA5"].value_counts()
Out[26]:
0 1908 1 1786 3 1582 2 1222 8 4 6 2 Name: H1DA5, dtype: int64
In [ ]:
Descriptive statistics height in foot and inches. Max of 98 or 99 is observed it is a code for no response or data not available.
In [27]:
data["H1GH59A"].describe()
Out[27]:
count 6504.000000 mean 6.283210 std 10.485217 min 4.000000 25% 5.000000 50% 5.000000 75% 5.000000 max 98.000000 Name: H1GH59A, dtype: float64
In [29]:
data["H1GH59B"].describe()
Out[29]:
count 6504.000000 mean 6.582565 std 11.582289 min 0.000000 25% 3.000000 50% 5.000000 75% 8.000000 max 99.000000 Name: H1GH59B, dtype: float64
In [30]:
data["H1DA8"].describe()
Out[30]:
count 6504.000000 mean 20.308272 std 64.930714 min 0.000000 25% 5.000000 50% 12.000000 75% 21.000000 max 998.000000 Name: H1DA8, dtype: float64
Filtering data based on height between 4 feet and 6 feet, tvhours watched perweek less than 50 hours/week, and excluding data on height, sport hours and weight with no responses.
In [9]:
sub1=data[(data['H1GH59A']>=4) & (data['H1GH59A']<=6) & (data['H1GH59B']<=12) & (data['H1DA5']<=3) & (data['H1GH60'] <= 500) ]
In [10]:Here my category explanatory variable is divided in tow bins with a value 0 for one of the bin
sub2 = sub1[(sub1["H1DA5"] == 0) | (sub1["H1DA5"] == 3)]
In [11]:
sub2['H1DA5'].value_counts()
Out[11]:
0 1830 3 1551 Name: H1DA5, dtype: int64
In [12]:
sub2['H1GH59A'].describe()
Out[12]:
count 3381.000000 mean 5.097308 std 0.389578 min 4.000000 25% 5.000000 50% 5.000000 75% 5.000000 max 6.000000 Name: H1GH59A, dtype: float64
In [13]:
sub2['H1GH59B'].describe()
Out[13]:
count 3381.000000 mean 5.208518 std 3.291193 min 0.000000 25% 3.000000 50% 5.000000 75% 8.000000 max 11.000000 Name: H1GH59B, dtype: float64
Caclulate height in inches
In [14]:
sub2['HEIGHT']=sub2['H1GH59A'] * 12 + sub2['H1GH59B']
C:\Users\haree\Anaconda3\lib\site-packages\ipykernel\__main__.py:1: SettingWithCopyWarning: A value is trying to be set on a copy of a slice from a DataFrame. Try using .loc[row_indexer,col_indexer] = value instead See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy if __name__ == '__main__':
In [15]:
sub2["HEIGHT"].describe()
Out[15]:
count 3381.000000 mean 66.376220 std 4.160516 min 50.000000 25% 63.000000 50% 66.000000 75% 69.000000 max 81.000000 Name: HEIGHT, dtype: float64
Below BMI is calculated using the following formula
Calculate BMI = 703 * Weight (lbs)/ height^2 (inch^2)
In [17]:
sub2['BMI'] = sub2.apply(lambda row: 703*row['H1GH60']/row['HEIGHT']**2, axis = 1)
C:\Users\haree\Anaconda3\lib\site-packages\ipykernel\__main__.py:1: SettingWithCopyWarning: A value is trying to be set on a copy of a slice from a DataFrame. Try using .loc[row_indexer,col_indexer] = value instead See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy if __name__ == '__main__':
Centering the response BMI by substracting mean from each data point
In [18]:
sub2['BMIcentered'] = sub2['BMI'] - sub2['BMI'].mean()
C:\Users\haree\Anaconda3\lib\site-packages\ipykernel\__main__.py:1: SettingWithCopyWarning: A value is trying to be set on a copy of a slice from a DataFrame. Try using .loc[row_indexer,col_indexer] = value instead See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy if __name__ == '__main__':
Verifying the BMI data is centered (check if mean is very close to zero).
In [31]:
sub2['BMIcentered'].mean()
Out[31]:This shows that mean of the centered variable is close to zero.
3.924692573297803e-15
In [32]:
sub2['H1DA5'].describe()
Out[32]:
count 3381.000000 mean 1.376220 std 1.495105 min 0.000000 25% 0.000000 50% 0.000000 75% 3.000000 max 3.000000 Name: H1DA5, dtype: float64
After preparing my explanatory variable which is active hours and response variable which is BMI the OLS model is applied to the data. Below are the results of the regression model.
OLS model
In [21]:
model1 = smf.ols(formula='BMIcentered ~ C(H1DA5)', data=sub2)
results1 = model1.fit()
print (results1.summary())
OLS Regression Results ============================================================================== Dep. Variable: BMIcentered R-squared: 0.004 Model: OLS Adj. R-squared: 0.004 Method: �� Least Squares F-statistic: 15.10 Date: Wed, 13 Dec 2017 Prob (F-statistic): 0.000104 Time: 12:42:08 Log-Likelihood: -9785.6 No. Observations: 3381 AIC: 1.958e+04 Df Residuals: 3379 BIC: 1.959e+04 Df Model: 1 Covariance Type: nonrobust ================================================================================= coef std err t P>|t| [0.025 0.975] --------------------------------------------------------------------------------- Intercept 0.2691 0.102 2.632 0.009 0.069 0.470 C(H1DA5)[T.3] -0.5867 0.151 -3.886 0.000 -0.883 -0.291 ============================================================================== Omnibus: 1135.249 Durbin-Watson: 1.932 Prob(Omnibus): 0.000 Jarque-Bera (JB): 4590.084 Skew: 1.610 Prob(JB): 0.00 Kurtosis: 7.714 Cond. No. 2.53 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
As we see from the results high F statistic and low P value (<0.05) proves that we can safely reject the null hypothesis. Also coefficient of the responsse variable is 0.2691 and slope is -0.5867. This can be fitted in to below equation
BMI=-0.5867*(Active hours)+0.2691
Evaluating Model fit:
Adding TVhours to the existing model
sub3 = sub2[(sub2['H1DA8’] > 0) & (sub2['H1DA8’] < 100)] sub3['H1DA8’] =pandas.to_numeric(sub3['H1DA8’], errors='coerce’)
Above non applicable data been removed from number of TV hours variable. Below regression model fit is again performed included TV hours
model2 = smf.ols(formula='BMIcentered ~ C(H1DA5) + H1DA8’, data=sub3) results2 = model2.fit() print (results2.summary())
OLS Regression Results ============================================================================== Dep. Variable: BMIcentered R-squared: 0.010 Model: OLS Adj. R-squared: 0.010 Method: Least Squares F-statistic: 17.10 Date: Sun, 17 Dec 2017 Prob (F-statistic): 4.08e-08 Time: 16:16:00 Log-Likelihood: -9516.9 No. Observations: 3287 AIC: 1.904e+04 Df Residuals: 3284 BIC: 1.906e+04 Df Model: 2 Covariance Type: nonrobust ================================================================================= coef std err t P>|t| [0.025 0.975] --------------------------------------------------------------------------------- Intercept -0.0640 0.132 -0.486 0.627 -0.322 0.194 C(H1DA5)[T.3] -0.5913 0.153 -3.858 0.000 -0.892 -0.291 H1DA8 0.0217 0.005 4.436 0.000 0.012 0.031 ============================================================================== Omnibus: 1090.035 Durbin-Watson: 1.934 Prob(Omnibus): 0.000 Jarque-Bera (JB): 4351.209 Skew: 1.592 Prob(JB): 0.00 Kurtosis: 7.651 Cond. No. 53.2 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Above results shows P value less that 0.01 for both TV hours and sport hours. Also t value is negative for Sport hours and positive for TV hours, proving that when TV hours are controlled Sport hours have negative effect on BMI,i.e as the spot hours increases BMI decreases. Also when spot hours are controlled as TVhours increases BMI increases. This also shows that both TV hours and Sport hours has considerable effect on the BMI of an individual
1 note
·
View note
Text
Week 4 Logistic Regression modelling Assignment
The data that I have used to perform Logistic Regression modelling is ADDHEALTH data provided. Below modules are imported for analyssis
import pandas import numpy import statsmodels.formula.api as smf import statsmodels.stats.multicomp as multi
Data analyzed is imported below
data = pandas.read_csv('addhealth.csv', low_memory=False)
Descriptive statistics of the variables that are being used for the analysis.
data["H1DA5"].describe()
count 6504.000000 mean 1.386839 std 1.158692 min 0.000000 25% 0.000000 50% 1.000000 75% 2.000000 max 8.000000 Name: H1DA5, dtype: float64
data["H1DA5"].value_counts()
0 1908 1 1786 3 1582 2 1222 8 4 6 2 Name: H1DA5, dtype: int64
data["H1GH59A"].describe()
count 6504.000000 mean 6.283210 std 10.485217 min 4.000000 25% 5.000000 50% 5.000000 75% 5.000000 max 98.000000 Name: H1GH59A, dtype: float64
data["H1GH59B"].describe()
count 6504.000000 mean 6.582565 std 11.582289 min 0.000000 25% 3.000000 50% 5.000000 75% 8.000000 max 99.000000 Name: H1GH59B, dtype: float64
Filtering data based on height between 4 feet and 6 feet, tvhours watched perweek less than 50 hours/week, and excluding data on height, sport hours and weight with no responses.
sub1=data[(data['H1GH59A']>=4) & (data['H1GH59A']<=6) & (data['H1GH59B']<=12) & (data['H1DA5']<=3) & (data['H1GH60'] <= 500) ]
Here my category explanatory variable is divided in tow bins with a value 0 for one of the bin
sub2 = sub1[(sub1["H1DA5"] == 0) | (sub1["H1DA5"] == 3)]
sub2['H1DA5'].value_counts()
0 1830 3 1551 Name: H1DA5, dtype: int64
sub2['H1GH59A'].describe()
count 3381.000000 mean 5.097308 std 0.389578 min 4.000000 25% 5.000000 50% 5.000000 75% 5.000000 max 6.000000 Name: H1GH59A, dtype: float64
sub2['H1GH59B'].describe()
count 3381.000000 mean 5.208518 std 3.291193 min 0.000000 25% 3.000000 50% 5.000000 75% 8.000000 max 11.000000 Name: H1GH59B, dtype: float64
Caclulate height in inches
In [12]:
sub2['HEIGHT']=sub2['H1GH59A'] * 12 + sub2['H1GH59B']
sub2["HEIGHT"].describe()
count 3381.000000 mean 66.376220 std 4.160516 min 50.000000 25% 63.000000 50% 66.000000 75% 69.000000 max 81.000000 Name: HEIGHT, dtype: float64
count 3381.000000 mean 66.376220 std 4.160516 min 50.000000 25% 63.000000 50% 66.000000 75% 69.000000 max 81.000000 Name: HEIGHT, dtype: float64
Weight descriptive statistics
sub2['H1GH60'].describe()
count 3381.000000 mean 140.859509 std 33.810411 min 57.000000 25% 118.000000 50% 135.000000 75% 158.000000 max 360.000000 Name: H1GH60, dtype: float64
Calculate BMI = 703 * Weight (lbs)/ height^2 (inch^2)
sub2['BMI'] = sub2.apply(lambda row: 703*row['H1GH60']/row['HEIGHT']**2, axis = 1)
Verifying the BMI data is centered (check if mean is very close to zero).
sub2['BMIcentered'].mean()
3.924692573297803e-15
Converting centered BMI to binary variable
susub3['BMIbinary'] = sub3['BMIcentered']<0
sub3['BMIbinary'] = sub3['BMIbinary'].astype('int')
sub3['BMIbinary']
0 0 1 1 3 0 4 0 6 0 10 1 14 1 17 0 19 0 20 1 21 1 23 1 24 0 26 0 28 0 32 1 36 1 37 1 38 1 40 1 42 1 44 1 47 1 48 0 49 0 50 1 52 1 55 1 57 0 58 0 .. 6444 1 6446 1 6447 1 6450 1 6451 1 6458 1 6459 0 6461 1 6462 0 6463 0 6465 0 6468 1 6469 1 6470 0 6472 1 6474 0 6475 1 6476 1 6480 1 6483 1 6484 1 6485 1 6488 0 6489 1 6493 1 6496 1 6497 0 6499 1 6502 0 6503 0 Name: BMIbinary, dtype: int32
In [35]:Performing logistic Regression below
model3 = smf.logit(formula='BMIbinary ~ C(H1DA5) + H1DA8', data=sub3)
results3 = model3.fit()
print (results3.summary())
Optimization terminated successfully. Current function value: 0.671880 Iterations 4 Logit Regression Results ============================================================================== Dep. Variable: BMIbinary No. Observations: 3287 Model: Logit Df Residuals: 3284 Method: MLE Df Model: 2 Date: Sun, 10 Dec 2017 Pseudo R-squ.: 0.003338 Time: 21:35:45 Log-Likelihood: -2208.5 converged: True LL-Null: -2215.9 LLR p-value: 0.0006137 ================================================================================= coef std err z P>|z| [0.025 0.975] --------------------------------------------------------------------------------- Intercept 0.4730 0.061 7.716 0.000 0.353 0.593 C(H1DA5)[T.3] 0.1174 0.072 1.640 0.101 -0.023 0.258 H1DA8 -0.0079 0.002 -3.499 0.000 -0.012 -0.003 =================================================================================
The above model shows that 3287 observations were used for analysis. Also sincce P value for H1DA5(Active hours) from bin 3 is greater than 0.000 that means knowing that the data point falls in to the ‘0′ bin for active hours and knowing H1DA8 (TVhours) is enough to predict the BMI binary variable.
Calculating Odd ratios
# odd ratios with 95% confidence intervals print ("Odds Ratios") params = results3.params conf = results3.conf_int() conf['OR'] = params conf.columns = ['Lower CI', 'Upper CI', 'OR'] print (numpy.exp(conf))
Below odd ratios show that TV hours from bin 3 has more oddds to estimate the BMI than TV hours.
Odds Ratios Lower CI Upper CI OR Intercept 1.423085 1.809621 1.604757 C(H1DA5)[T.3] 0.977349 1.293966 1.124569 H1DA8 0.987767 0.996536 0.992142
0 notes
Text
Regression Modelling Week 3 Assignment- Multiple Regression-Confounding variables
The data that I used for multiple regression is addhealth data. Below are the decriptions of the vraibales used in the analysis.
"H1DA5"= Sport hours
H1GH59A"= Height part in foot
H1GH59B"= Height part in inches
"H1DA8"= TV hours
Below I am importing the stats models and reading the data
import pandas import numpy import statsmodels.formula.api as smf import statsmodels.stats.multicomp as multi
data = pandas.read_csv('addhealth.csv', low_memory=False)
Descriptive statistics for number of hours active in sports per week. In [25]:
data["H1DA5"].describe()
Out[25]:
count 6504.000000 mean 1.386839 std 1.158692 min 0.000000 25% 0.000000 50% 1.000000 75% 2.000000 max 8.000000 Name: H1DA5, dtype: float64
In [26]:
data["H1DA5"].value_counts()
Out[26]:
0 1908 1 1786 3 1582 2 1222 8 4 6 2 Name: H1DA5, dtype: int64
In [ ]:
Descriptive statistics height in foot and inches. Max of 98 or 99 is observed it is a code for no response or data not available.
In [27]:
data["H1GH59A"].describe()
Out[27]:
count 6504.000000 mean 6.283210 std 10.485217 min 4.000000 25% 5.000000 50% 5.000000 75% 5.000000 max 98.000000 Name: H1GH59A, dtype: float64
In [29]:
data["H1GH59B"].describe()
Out[29]:
count 6504.000000 mean 6.582565 std 11.582289 min 0.000000 25% 3.000000 50% 5.000000 75% 8.000000 max 99.000000 Name: H1GH59B, dtype: float64
In [30]:
data["H1DA8"].describe()
Out[30]:
count 6504.000000 mean 20.308272 std 64.930714 min 0.000000 25% 5.000000 50% 12.000000 75% 21.000000 max 998.000000 Name: H1DA8, dtype: float64
Filtering data based on height between 4 feet and 6 feet, tvhours watched perweek less than 50 hours/week, and excluding data on height, sport hours and weight with no responses.
In [9]:
sub1=data[(data['H1GH59A']>=4) & (data['H1GH59A']<=6) & (data['H1GH59B']<=12) & (data['H1DA5']<=3) & (data['H1GH60'] <= 500) ]
In [10]:Here my category explanatory variable is divided in tow bins with a value 0 for one of the bin
sub2 = sub1[(sub1["H1DA5"] == 0) | (sub1["H1DA5"] == 3)]
In [11]:
sub2['H1DA5'].value_counts()
Out[11]:
0 1830 3 1551 Name: H1DA5, dtype: int64
In [12]:
sub2['H1GH59A'].describe()
Out[12]:
count 3381.000000 mean 5.097308 std 0.389578 min 4.000000 25% 5.000000 50% 5.000000 75% 5.000000 max 6.000000 Name: H1GH59A, dtype: float64
In [13]:
sub2['H1GH59B'].describe()
Out[13]:
count 3381.000000 mean 5.208518 std 3.291193 min 0.000000 25% 3.000000 50% 5.000000 75% 8.000000 max 11.000000 Name: H1GH59B, dtype: float64
Caclulate height in inches
In [14]:
sub2['HEIGHT']=sub2['H1GH59A'] * 12 + sub2['H1GH59B']
C:\Users\haree\Anaconda3\lib\site-packages\ipykernel\__main__.py:1: SettingWithCopyWarning: A value is trying to be set on a copy of a slice from a DataFrame. Try using .loc[row_indexer,col_indexer] = value instead See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy if __name__ == '__main__':
In [15]:
sub2["HEIGHT"].describe()
Out[15]:
count 3381.000000 mean 66.376220 std 4.160516 min 50.000000 25% 63.000000 50% 66.000000 75% 69.000000 max 81.000000 Name: HEIGHT, dtype: float64
Below BMI is calculated using the following formula
Calculate BMI = 703 * Weight (lbs)/ height^2 (inch^2)
In [17]:
sub2['BMI'] = sub2.apply(lambda row: 703*row['H1GH60']/row['HEIGHT']**2, axis = 1)
C:\Users\haree\Anaconda3\lib\site-packages\ipykernel\__main__.py:1: SettingWithCopyWarning: A value is trying to be set on a copy of a slice from a DataFrame. Try using .loc[row_indexer,col_indexer] = value instead See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy if __name__ == '__main__':
Centering the response BMI by substracting mean from each data point
In [18]:
sub2['BMIcentered'] = sub2['BMI'] - sub2['BMI'].mean()
C:\Users\haree\Anaconda3\lib\site-packages\ipykernel\__main__.py:1: SettingWithCopyWarning: A value is trying to be set on a copy of a slice from a DataFrame. Try using .loc[row_indexer,col_indexer] = value instead See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy if __name__ == '__main__':
Verifying the BMI data is centered (check if mean is very close to zero).
In [31]:
sub2['BMIcentered'].mean()
Out[31]:This shows that mean of the centered variable is close to zero.
3.924692573297803e-15
In [32]:
sub2['H1DA5'].describe()
Out[32]:
count 3381.000000 mean 1.376220 std 1.495105 min 0.000000 25% 0.000000 50% 0.000000 75% 3.000000 max 3.000000 Name: H1DA5, dtype: float64
After preparing my explanatory variable which is active hours and response variable which is BMI the OLS model is applied to the data. Below are the results of the regression model.
OLS model
In [21]:
model1 = smf.ols(formula='BMIcentered ~ C(H1DA5)', data=sub2)
results1 = model1.fit()
print (results1.summary())
OLS Regression Results ============================================================================== Dep. Variable: BMIcentered R-squared: 0.004 Model: OLS Adj. R-squared: 0.004 Method: Least Squares F-statistic: 15.10 Date: Wed, 13 Dec 2017 Prob (F-statistic): 0.000104 Time: 12:42:08 Log-Likelihood: -9785.6 No. Observations: 3381 AIC: 1.958e+04 Df Residuals: 3379 BIC: 1.959e+04 Df Model: 1 Covariance Type: nonrobust ================================================================================= coef std err t P>|t| [0.025 0.975] --------------------------------------------------------------------------------- Intercept 0.2691 0.102 2.632 0.009 0.069 0.470 C(H1DA5)[T.3] -0.5867 0.151 -3.886 0.000 -0.883 -0.291 ============================================================================== Omnibus: 1135.249 Durbin-Watson: 1.932 Prob(Omnibus): 0.000 Jarque-Bera (JB): 4590.084 Skew: 1.610 Prob(JB): 0.00 Kurtosis: 7.714 Cond. No. 2.53 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
As we see from the results high F statistic and low P value (<0.05) proves that we can safely reject the null hypothesis. Also coefficient of the responsse variable is 0.2691 and slope is -0.5867. This can be fitted in to below equation
BMI=-0.5867*(Active hours)+0.2691
Evaluating Model fit:
Adding TVhours to the existing model
sub3 = sub2[(sub2['H1DA8'] > 0) & (sub2['H1DA8'] < 100)] sub3['H1DA8'] =pandas.to_numeric(sub3['H1DA8'], errors='coerce')
Above non applicable data been removed from number of TV hours variable. Below regression model fit is again performed included TV hours
model2 = smf.ols(formula='BMIcentered ~ C(H1DA5) + H1DA8', data=sub3) results2 = model2.fit() print (results2.summary())
OLS Regression Results ============================================================================== Dep. Variable: BMIcentered R-squared: 0.010 Model: OLS Adj. R-squared: 0.010 Method: Least Squares F-statistic: 17.10 Date: Sun, 17 Dec 2017 Prob (F-statistic): 4.08e-08 Time: 16:16:00 Log-Likelihood: -9516.9 No. Observations: 3287 AIC: 1.904e+04 Df Residuals: 3284 BIC: 1.906e+04 Df Model: 2 Covariance Type: nonrobust ================================================================================= coef std err t P>|t| [0.025 0.975] --------------------------------------------------------------------------------- Intercept -0.0640 0.132 -0.486 0.627 -0.322 0.194 C(H1DA5)[T.3] -0.5913 0.153 -3.858 0.000 -0.892 -0.291 H1DA8 0.0217 0.005 4.436 0.000 0.012 0.031 ============================================================================== Omnibus: 1090.035 Durbin-Watson: 1.934 Prob(Omnibus): 0.000 Jarque-Bera (JB): 4351.209 Skew: 1.592 Prob(JB): 0.00 Kurtosis: 7.651 Cond. No. 53.2 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Above results shows P value less that 0.01 for both TV hours and sport hours. Also t value is negative for Sport hours and positive for TV hours, proving that when TV hours are controlled Sport hours have negative effect on BMI,i.e as the spot hours increases BMI decreases. Also when spot hours are controlled as TVhours increases BMI increases. This also shows that both TV hours and Sport hours has considerable effect on the BMI of an individual
Below are some of the plots #Q-Q plot for normality fig4=sm.qqplot(results2.resid, line='r')
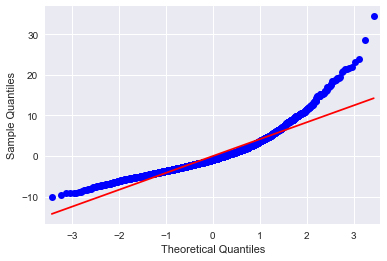
# simple plot of residuals stdres=pandas.DataFrame(results2.resid_pearson) plt.plot(stdres, 'o', ls='None') l = plt.axhline(y=0, color='r') plt.ylabel('Standardized Residual') plt.xlabel('Observation Number')
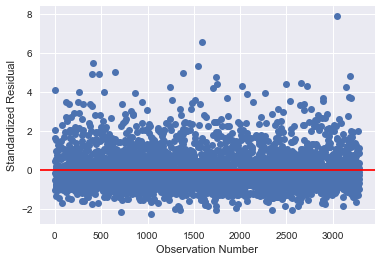
# additional regression diagnostic plots fig2 = plt.figure() fig2 = sm.graphics.plot_regress_exog(results2, "H1DA8", fig=fig2)

1 note
·
View note
Text
Regression Modelling week2 Assignment
import pandas import numpy import statsmodels.formula.api as smf import statsmodels.stats.multicomp as multi
The data that I used to test my basic linear regression model is ADDHEALTH data. The variables that I used are number active hours to BMI calculated from the weight and height data of the sample given. Data has been filtered to remove outliers like misssings and unknowns. Then the active hours are filtered and divided in to two bins (’0′ and ‘3′) as shown below.
data = pandas.read_csv('addhealth.csv', low_memory=False)
sub1=data[(data['H1GH59A']>=4) & (data['H1GH59A']<=6) & (data['H1GH59B']<=12) & (data['H1DA5']<=3) & (data['H1GH60'] <= 500) ]
sub2 = sub1[(sub1["H1DA5"] == 0) | (sub1["H1DA5"] == 3)]
sub2['H1DA5'].value_counts()
0 1830 3 1551 Name: H1DA5, dtype: int64
sub2['H1GH59A'].describe()
sub2['HEIGHT']=sub2['H1GH59A'] * 12 + sub2['H1GH59B']
Height is converted to inches in the above calculation
sub2['BMI'] = sub2.apply(lambda row: 703*row['H1GH60']/row['HEIGHT']**2, axis = 1)
In the above calculation BMI is calculated using height in inches (HEIGHT) and weight in pounds (HIGH60)
Centering the response BMI by substracting mean from each data point
sub2['BMIcentered'] = sub2['BMI'] - sub2['BMI'].mean()
Verifying the BMI data is centered (check if mean is very close to zero).
In [17]:
sub2['BMIcentered'].mean()
Out[17]:
3.924692573297803e-15
After collapsing my categorical explanatory variable I have applied my logistic model to the variables that I selected
OLS model
In [18]:
model1 = smf.ols(formula='BMIcentered ~ C(H1DA5)', data=sub2)
results1 = model1.fit()
print (results1.summary())
OLS Regression Results ============================================================================== Dep. Variable: BMIcentered R-squared: 0.004 Model: OLS Adj. R-squared: 0.004 Method: Least Squares F-statistic: 15.10 Date: Sun, 10 Dec 2017 Prob (F-statistic): 0.000104 Time: 20:45:40 Log-Likelihood: -9785.6 No. Observations: 3381 AIC: 1.958e+04 Df Residuals: 3379 BIC: 1.959e+04 Df Model: 1 Covariance Type: nonrobust ================================================================================= coef std err t P>|t| [0.025 0.975] --------------------------------------------------------------------------------- Intercept 0.2691 0.102 2.632 0.009 0.069 0.470 C(H1DA5)[T.3] -0.5867 0.151 -3.886 0.000 -0.883 -0.291 ============================================================================== Omnibus: 1135.249 Durbin-Watson: 1.932 Prob(Omnibus): 0.000 Jarque-Bera (JB): 4590.084 Skew: 1.610 Prob(JB): 0.00 Kurtosis: 7.714 Cond. No. 2.53 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Summary:
From the below model a total of 3381 observation are being used in the model. As we notice P value is less than 0.05 and thus proves that we can safely reject the null hypothesis. Also p>T is 0.000 and coefficients of the explanatory variable is -0.5867 and the intercept is 0.2691. o the quation can be written as
BMI=-0.5867*(Sport hours)+0.2691
0 notes
Text
Regression Week1 Assignment
Sample: The National Longitudinal Study of Adolescent Health (AddHealth) is a representative school-based survey of adolescents in grades 7-12 in the United States. The Wave 1 survey focuses on factors that may influence adolescents’ health and risk behaviors, including personal traits, families, friendships, romantic relationships, peer groups, schools, neighborhoods, and communities. A sample of 6504 randomly selected data is used to study the effect of sports on weight of the individuals.
Procedures: Unequal probability techniques used to select samples of students for 132 schools across US. In school questionnaire is used to downselect the samples to address the variability. Surveying techniques utilized to collect data which is both categorical and continuous.
Measures: The measures for this data are weight that is measured in pounds and the intensity of sports activity is measured hours of sports played per week. For the purpose of this analysis, the weight is binned into 4 equal quartiles, Not applicable values are filtered out. Also sport hours/week is binned into 3 bins and no data available groups are excluded.
0 notes
Text
Week 4 Assignment-ANOVA with moderator
This is test the association of moderator on an ANOVA performed on data related to TV hours and BMI. The moderator that has been selected for this is number of hours that the person spends playing sports. Two different bins were created based on the hours spent on sports. Below are the steps performed to illustrate this.
import numpy import pandas import statsmodels.formula.api as smf import statsmodels.stats.multicomp as multi import seaborn import matplotlib.pyplot as plt
%matplotlib inline
data = pandas.read_csv('addhealth.csv', low_memory=False) sub1=data[(data['H1GH59A']>=4) & (data['H1GH59A']<=6) & (data['H1GH59B']<=12) & (data['H1DA8']<=50) & (data['H1GH60'] <= 500)] sub1['HEIGHT']=sub1['H1GH59A'] * 12 + sub1['H1GH59B'] sub1['BMI'] = sub1.apply(lambda row: 703*row['H1GH60']/row['HEIGHT']**2, axis = 1) sub1['TVHOURS'] = pandas.cut(sub1['H1DA8'], bins=[-1, 18, 50], labels=False)
Above code prepares the data, calculate BMI and create bins for TV hours.
Below code performs ANOVA test to test the null hypothesis if there is any significant association between TVHOURS and BMI.
model1 = smf.ols(formula='BMI ~ C(TVHOURS)', data=sub1) results1 = model1.fit() print (results1.summary())
OLS Regression Results ============================================================================== Dep. Variable: BMI R-squared: 0.003 Model: OLS Adj. R-squared: 0.002 Method: Least Squares F-statistic: 15.46 Date: Mon, 16 Oct 2017 Prob (F-statistic): 8.54e-05 Time: 21:22:21 Log-Likelihood: -17595. No. Observations: 6075 AIC: 3.519e+04 Df Residuals: 6073 BIC: 3.521e+04 Df Model: 1 Covariance Type: nonrobust =================================================================================== coef std err t P>|t| [0.025 0.975] ----------------------------------------------------------------------------------- Intercept 22.2878 0.068 326.091 0.000 22.154 22.422 C(TVHOURS)[T.1] 0.4726 0.120 3.931 0.000 0.237 0.708 ============================================================================== Omnibus: 1830.021 Durbin-Watson: 1.936 Prob(Omnibus): 0.000 Jarque-Bera (JB): 6299.655 Skew: 1.502 Prob(JB): 0.00 Kurtosis: 6.983 Cond. No. 2.42 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Above results show a significant F statistic and a significant P value to safely reject null hypothesis, thus stating the there is significant association between TVHOURS and BMI.
sub2 = sub1[['BMI', 'TVHOURS','H1DA5']].dropna() print ('means for BMI by TVHOURS') m1= sub2.groupby('TVHOURS').mean() print (m1)
standard deviations for BMI by TVHOURS BMI H1DA5 TVHOURS 0 4.224927 1.14882 1 4.694750 1.13441
print ('standard deviations for BMI by TVHOURS')
sd1 = sub2.groupby('TVHOURS').std()
print (sd1)
standard deviations for BMI by TVHOURS BMI H1DA5 TVHOURS 0 4.224927 1.14882 1 4.694750 1.13441
In [7]:seaborn.factorplot(x="TVHOURS", y="BMI", data=sub2, kind="bar", ci=None) plt.xlabel('TV hours') plt.ylabel('BMI')

Below are the steps to prepare the moderator, which is the number of sport hours.
#Sport hours buckets sub3=sub2[(sub2['H1DA5']<2)] sub4=sub2[(sub2['H1DA5']>1) & ((sub2['H1DA5']<4))]
Below are the steps to test the association of the moderator
print ('association between TV hours and BMI for those with low sport hours') model2 = smf.ols(formula='BMI ~ C(TVHOURS)', data=sub3).fit() print (model2.summary())
print ('association between TV hours and BMI for those with high sport hours') model3 = smf.ols(formula='BMI ~ C(TVHOURS)', data=sub4).fit() print (model3.summary())
association between TV hours and BMI for those with low sport hours OLS Regression Results ============================================================================== Dep. Variable: BMI R-squared: 0.004 Model: OLS Adj. R-squared: 0.003 Method: Least Squares F-statistic: 12.53 Date: Mon, 16 Oct 2017 Prob (F-statistic): 0.000405 Time: 21:35:03 Log-Likelihood: -10040. No. Observations: 3422 AIC: 2.008e+04 Df Residuals: 3420 BIC: 2.010e+04 Df Model: 1 Covariance Type: nonrobust =================================================================================== coef std err t P>|t| [0.025 0.975] ----------------------------------------------------------------------------------- Intercept 22.4306 0.095 236.409 0.000 22.245 22.617 C(TVHOURS)[T.1] 0.5866 0.166 3.540 0.000 0.262 0.911 ============================================================================== Omnibus: 929.445 Durbin-Watson: 1.967 Prob(Omnibus): 0.000 Jarque-Bera (JB): 2572.870 Skew: 1.428 Prob(JB): 0.00 Kurtosis: 6.145 Cond. No. 2.41 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. association between TV hours and BMI for those with high sport hours OLS Regression Results ============================================================================== Dep. Variable: BMI R-squared: 0.001 Model: OLS Adj. R-squared: 0.001 Method: Least Squares F-statistic: 3.251 Date: Mon, 16 Oct 2017 Prob (F-statistic): 0.0715 Time: 21:35:03 Log-Likelihood: -7535.5 No. Observations: 2653 AIC: 1.508e+04 Df Residuals: 2651 BIC: 1.509e+04 Df Model: 1 Covariance Type: nonrobust =================================================================================== coef std err t P>|t| [0.025 0.975] ----------------------------------------------------------------------------------- Intercept 22.1066 0.097 226.985 0.000 21.916 22.298 C(TVHOURS)[T.1] 0.3117 0.173 1.803 0.071 -0.027 0.651 ============================================================================== Omnibus: 913.565 Durbin-Watson: 1.926 Prob(Omnibus): 0.000 Jarque-Bera (JB): 4271.089 Skew: 1.591 Prob(JB): 0.00 Kurtosis: 8.340 Cond. No. 2.42 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Above results show that the p value is significant when associated with high sport hours where as p value is non significant while associated with less sport hours. Thus proving that the sport hours in this case moderated the association.
Below are the means that prove the same.
print ("means for BMI by TV hours low vs. high for low sport hours") m3= sub3.groupby('TVHOURS').mean() print (m3) print ("means for BMI by TV hours low vs. high for high sport hours") m4 = sub4.groupby('TVHOURS').mean() print (m4)
means for BMI by TV hours low vs. high for low sport hours �� BMI H1DA5 TVHOURS 0 22.430561 0.478696 1 23.017167 0.496435 means for BMI by TV hours low vs. high for high sport hours BMI H1DA5 TVHOURS 0 22.106589 2.563777 1 22.418312 2.554632
0 notes
Text
Pearson Correlation Coefficient on Nesarc data
Pearson Correlation coefficient is used to see if there is any relation ship between number of cigarettes smoking frequency and frequency of wine consumption in the last twelve months. “nesarc.csv” data has been used for the above research question.
Null hypothesis: cigarette smoking frequency has no effect on wine consumption frequency in last 12 months.
Below are the steps that are being followed to test the null hypothesis as both the variables are quantitative variables.
import pandas import numpy import seaborn import scipy import matplotlib.pyplot as plt
Importing data
data = pandas.read_csv('nesarc.csv', low_memory=False)
Variables considered for analysis
data['freqcigar'] = data['S3AQ3B1'].convert_objects(convert_numeric=True) data['freqwine'] = data['S2AQ6B'].convert_objects(convert_numeric=True)
data_clean=data.dropna()
Missing values or na values are removed since the pearson correlation cannot be performed on these values.
Deriving pearson correlation coefficient for the variables
print ('association between urbanrate and internetuserate') print (scipy.stats.pearsonr(data_clean['freqcigar'], data_clean['freqwine']))
association between cigerette frequency and wine frequency (-0.004687362914961221, 0.70056965411366912)
Above p value shows that the null hypothesis can be safely accepted and that there is no relation ship between cigarette smoking individuals drinking more wine or the consuming wine frequency.
the value of r2 for the test performed is 0.000022 which shows that if the we know the number of cigarettes smoked by a person there is only 0.002 percent variability in frequency of wine drinking can be predicted which is very negligible again supporting the null hypothesis.
Thus our above test can be concluded as accepting null hypothesis.
0 notes
Text
ChiSquare test on ADDHEALTH Data
This test is performed to determine if there is a relationship between Race/Ethnicity on the grades of mathematics on the students. Below data and functions is being imported.
Null Hypothesis: Race has no effect on mathematics grades of students
import pandas import numpy import scipy.stats import seaborn import matplotlib.pyplot as plt %matplotlib inline
In [3]:
data = pandas.read_csv('addhealth.csv', low_memory=False)
Below are the variables selected.H1GI8 is Race,H1ED12 is Grade and data filters are applied to remove unknowns and non applicable values for these values to select only valid data for analysis
data2=data[['H1GI8','H1ED12']]
data3 = data2[(data2['H1GI8'] < 5) & (data2['H1ED12'] < 5)] data3['GRADE'] = pandas.cut(data3['H1ED12'], bins=[0, 2, 4], labels=False)
Grade is divided above in to two bins.
# contingency table of observed counts ct1=pandas.crosstab(data3['GRADE'], data3['H1GI8']) print (ct1) H1GI8 1 2 3 4 GRADE 0 62 42 18 15 1 55 42 11 9
Observed counts are calculated above
# column percentages colsum=ct1.sum(axis=0) colpct=ct1/colsum print(colpct)
H1GI8 1 2 3 4 GRADE 0 0.529915 0.5 0.62069 0.625 1 0.470085 0.5 0.37931 0.375
Column percentages are calculated above. Above percentages show that there is no huge difference between the proportion of observed counts for higher grades.
# chi-square print ('chi-square value, p value, expected counts') cs1= scipy.stats.chi2_contingency(ct1) print (cs1)
chi-square value, p value, expected counts (2.0463427922978612, 0.56284401061125688, 3, array([[ 63.10629921, 45.30708661, 15.64173228, 12.94488189], [ 53.89370079, 38.69291339, 13.35826772, 11.05511811]]))
Chi Square test of independence is performed above. From the test although the chi square value is not too high and the p value is more than 0.05 , so we can accept the null hypothesis or failed to reject null hypothesis. Below it is further proved by performing postdoc test for the paired comparisons on ethnicity.
# set variable types data3["H1GI8"] = data3["H1GI8"].astype('category') # new code for setting variables to numeric: data3['GRADE'] = pandas.to_numeric(data3['GRADE'], errors='coerce') # graph percent with Grade dependence within each Race seaborn.factorplot(x="H1GI8", y="GRADE", data=data3, kind="bar", ci=None) plt.xlabel('RACE') plt.ylabel('Grade Achieved')
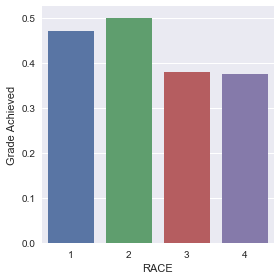
Post Hoc tests on Paired comparisons.
For this test we have 6 paired comparisons. [(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)]
So the Bonferroni corrected probability is 0.05/6 which is 0.08
Below is the code used to perform paired comparisons
recode2={1:1,2:2} data3['comp1v2']=data3['H1GI8'].map(recode2) colsum=ct2.sum(axis=0) colpct=ct2/colsum print(colpct) # chi-square on first pair print ('chi-square value, p value, expected counts') cs2= scipy.stats.chi2_contingency(ct2) print (cs2)
comp1v2 1.0 2.0 GRADE 0 0.529915 0.5 1 0.470085 0.5 chi-square value, p value, expected counts (0.0759080394724225, 0.78292126648730009, 1, array([[ 60.53731343, 43.46268657], [ 56.46268657, 40.53731343]]))
C:\Users\haree\Anaconda3\lib\site-packages\ipykernel\__main__.py:2: SettingWithCopyWarning: A value is trying to be set on a copy of a slice from a DataFrame. Try using .loc[row_indexer,col_indexer] = value instead See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy from ipykernel import kernelapp as app
In [25]:
In [31]:
recode3={1:1,3:3} data3['comp1v3']=data3['H1GI8'].map(recode3) ct3=pandas.crosstab(data3['GRADE'], data3['comp1v3']) print (ct3) colsum=ct3.sum(axis=0) colpct=ct3/colsum print(colpct) # chi-square on second pair print ('chi-square value, p value, expected counts') cs3= scipy.stats.chi2_contingency(ct3) print (cs3)
comp1v3 1.0 3.0 GRADE 0 62 18 1 55 11 comp1v3 1.0 3.0 GRADE 0 0.529915 0.62069 1 0.470085 0.37931 chi-square value, p value, expected counts (0.45006039618108573, 0.50230627457489929, 1, array([[ 64.10958904, 15.89041096], [ 52.89041096, 13.10958904]]))
C:\Users\haree\Anaconda3\lib\site-packages\ipykernel\__main__.py:2: SettingWithCopyWarning: A value is trying to be set on a copy of a slice from a DataFrame. Try using .loc[row_indexer,col_indexer] = value instead See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy from ipykernel import kernelapp as app
In [32]:
recode4={1:1,4:4} data3['comp1v4']=data3['H1GI8'].map(recode4) ct4=pandas.crosstab(data3['GRADE'], data3['comp1v4']) print (ct4) colsum=ct4.sum(axis=0) colpct=ct4/colsum print(colpct) # chi-square on third pair print ('chi-square value, p value, expected counts') cs4= scipy.stats.chi2_contingency(ct4) print (cs4)
comp1v4 1.0 4.0 GRADE 0 62 15 1 55 9 comp1v4 1.0 4.0 GRADE 0 0.529915 0.625 1 0.470085 0.375 chi-square value, p value, expected counts (0.39343810486388614, 0.53049770166479027, 1, array([[ 63.89361702, 13.10638298], [ 53.10638298, 10.89361702]]))
C:\Users\haree\Anaconda3\lib\site-packages\ipykernel\__main__.py:2: SettingWithCopyWarning: A value is trying to be set on a copy of a slice from a DataFrame. Try using .loc[row_indexer,col_indexer] = value instead See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy from ipykernel import kernelapp as app
In [33]:
recode5={2:2,3:3} data3['comp1v5']=data3['H1GI8'].map(recode5) ct5=pandas.crosstab(data3['GRADE'], data3['comp1v5']) print (ct5) colsum=ct5.sum(axis=0) colpct=ct5/colsum print(colpct) # chi-square on fourth pair print ('chi-square value, p value, expected counts') cs5= scipy.stats.chi2_contingency(ct5) print (cs5)
comp1v5 2.0 3.0 GRADE 0 42 18 1 42 11 comp1v5 2.0 3.0 GRADE 0 0.5 0.62069 1 0.5 0.37931 chi-square value, p value, expected counts (0.82281323259080297, 0.36435892466929332, 1, array([[ 44.60176991, 15.39823009], [ 39.39823009, 13.60176991]]))
C:\Users\haree\Anaconda3\lib\site-packages\ipykernel\__main__.py:2: SettingWithCopyWarning: A value is trying to be set on a copy of a slice from a DataFrame. Try using .loc[row_indexer,col_indexer] = value instead See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy from ipykernel import kernelapp as app
In [34]:
recode6={2:2,4:4} data3['comp1v6']=data3['H1GI8'].map(recode6) ct6=pandas.crosstab(data3['GRADE'], data3['comp1v6']) print (ct6) colsum=ct6.sum(axis=0) colpct=ct6/colsum print(colpct) # chi-square on fourth pair print ('chi-square value, p value, expected counts') cs6= scipy.stats.chi2_contingency(ct6) print (cs6)
comp1v6 2.0 4.0 GRADE 0 42 15 1 42 9 comp1v6 2.0 4.0 GRADE 0 0.5 0.625 1 0.5 0.375 chi-square value, p value, expected counts (0.72246793454223868, 0.39533557316654266, 1, array([[ 44.33333333, 12.66666667], [ 39.66666667, 11.33333333]]))
C:\Users\haree\Anaconda3\lib\site-packages\ipykernel\__main__.py:2: SettingWithCopyWarning: A value is trying to be set on a copy of a slice from a DataFrame. Try using .loc[row_indexer,col_indexer] = value instead See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy from ipykernel import kernelapp as app
In [35]:
recode7={3:3,4:4} data3['comp1v7']=data3['H1GI8'].map(recode7) ct7=pandas.crosstab(data3['GRADE'], data3['comp1v7']) print (ct7) colsum=ct7.sum(axis=0) colpct=ct7/colsum print(colpct) # chi-square on fourth pair print ('chi-square value, p value, expected counts') cs7= scipy.stats.chi2_contingency(ct7) print (cs7)
comp1v7 3.0 4.0 GRADE 0 18 15 1 11 9 comp1v7 3.0 4.0 GRADE 0 0.62069 0.625 1 0.37931 0.375 chi-square value, p value, expected counts (0.063717454719609878, 0.80071399590897796, 1, array([[ 18.05660377, 14.94339623], [ 10.94339623, 9.05660377]]))
C:\Users\haree\Anaconda3\lib\site-packages\ipykernel\__main__.py:2: SettingWithCopyWarning: A value is trying to be set on a copy of a slice from a DataFrame. Try using .loc[row_indexer,col_indexer] = value instead See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy from ipykernel import kernelapp as app
Inference:
Below table shows that all the probabilities of the paired comparison chi square test performed have P value much greater than our Bonferroni corrected P values which is 0.08, thus further proving that we can safely accept the null hypothesis, which is that there is no effect of Race on mathematics grades of students.

0 notes
Text
ANOVA test on ADDHEALTH data
This is a blog about ANOVA test for ADDHEALTH data.
Data: The National Longitudinal Study of Adolescent Health (AddHealth) is a representative school-based survey of adolescents in grades 7-12 in the United States. The Wave 1 survey focuses on factors that may influence adolescents’ health and risk behaviors, including personal traits, families, friendships, romantic relationships, peer groups, schools, neighborhoods, and communities.
Research Question: Is BMI of the population sample dependent on the number of TV hours watched
Null Hypothesis: BMI of the subjects on sample are not effected by number of Television hours per week
Number of hours per week has been categorized in to three bins. -1- 7, 7-18, 18-50 to see mean differences between the groups. Thus ANOVA has been used to analyze this research question since more than two levels are involved.
Below the steps performed to reach the data sample have been explained .
The following snippets of code is written in python to read data and perform the analysis.
import pandas import numpy import statsmodels.formula.api as smf import statsmodels.stats.multicomp as multi
data = pandas.read_csv('addhealth.csv', low_memory=False)
Below are the descriptive statistics for number of hours of TV watched per week. There are total of 6504 observations. The max of 998 is not realistic. Upon cross reference with code book, this means data is missing or refused by subject.
data["H1DA8"].describe()
count 6504.000000 mean 20.308272 std 64.930714 min 0.000000 25% 5.000000 50% 12.000000 75% 21.000000 max 998.000000 Name: H1DA8, dtype: float64
Below are the descriptive statistics height columns in foot and inches. Max of 98 or 99 is observed it is a code for no response or data not available.
data["H1GH59A"].describe()
count 6504.000000 mean 6.283210 std 10.485217 min 4.000000 25% 5.000000 50% 5.000000 75% 5.000000 max 98.000000 Name: H1GH59A, dtype: float64
In [5]:
data["H1GH59B"].describe()
Out[5]:
count 6504.000000 mean 6.582565 std 11.582289 min 0.000000 25% 3.000000 50% 5.000000 75% 8.000000 max 99.000000 Name: H1GH59B, dtype: float64
Filtering data based on height between 4 feet and 6 feet, tvhours watched perweek less than 50 hours/week, and excluding data on height, TV hours and weight with no responses.
In [6]:
sub1=data[(data['H1GH59A']>=4) & (data['H1GH59A']<=6) & (data['H1GH59B']<=12) & (data['H1DA8']<=50) & (data['H1GH60'] <= 500)]
In [7]:
sub1['H1GH59A'].describe()
Out[7]:
count 6075.000000 mean 5.086914 std 0.381950 min 4.000000 25% 5.000000 50% 5.000000 75% 5.000000 max 6.000000 Name: H1GH59A, dtype: float64
sub1['H1GH59B'].describe()
Out[8]:
count 6075.000000 mean 5.244774 std 3.269102 min 0.000000 25% 3.000000 50% 5.000000 75% 8.000000 max 11.000000 Name: H1GH59B, dtype: float64
Caclulate height in inches
In [9]:
sub1['HEIGHT']=sub1['H1GH59A'] * 12 + sub1['H1GH59B']
C:\Users\haree\Anaconda3\lib\site-packages\ipykernel\__main__.py:1: SettingWithCopyWarning: A value is trying to be set on a copy of a slice from a DataFrame. Try using .loc[row_indexer,col_indexer] = value instead See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy if __name__ == '__main__':
In [10]:
sub1["HEIGHT"].describe()
Out[10]:
count 6075.000000 mean 66.287737 std 4.121049 min 48.000000 25% 63.000000 50% 66.000000 75% 69.000000 max 81.000000 Name: HEIGHT, dtype: float64
Weight descriptive statistics
In [11]:
sub1['H1GH60'].describe()
Out[11]:
count 6075.000000 mean 141.106831 std 34.074604 min 50.000000 25% 118.000000 50% 135.000000 75% 160.000000 max 360.000000 Name: H1GH60, dtype: float64
Calculate BMI = 703 * Weight (lbs)/ height^2 (inch^2)
In [12]:
sub1['BMI'] = sub1.apply(lambda row: 703*row['H1GH60']/row['HEIGHT']**2, axis = 1)
C:\Users\haree\Anaconda3\lib\site-packages\ipykernel\__main__.py:1: SettingWithCopyWarning: A value is trying to be set on a copy of a slice from a DataFrame. Try using .loc[row_indexer,col_indexer] = value instead See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy if __name__ == '__main__':
Convert TVHOURS into categorical variable with 4 bins -1 to 7, 7 to 18, 18 to 50
In [13]:
sub1['TVHOURS'] = pandas.cut(sub1['H1DA8'], bins=[-1, 7, 18, 50], labels=False)
C:\Users\haree\Anaconda3\lib\site-packages\ipykernel\__main__.py:1: SettingWithCopyWarning: A value is trying to be set on a copy of a slice from a DataFrame. Try using .loc[row_indexer,col_indexer] = value instead See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy if __name__ == '__main__':
In [14]:
model1 = smf.ols(formula='BMI ~ C(TVHOURS)', data=sub1) results1 = model1.fit() print (results1.summary())
OLS Regression Results ============================================================================== Dep. Variable: BMI R-squared: 0.003 Model: OLS Adj. R-squared: 0.003 Method: Least Squares F-statistic: 9.690 Date: Sun, 16 Jul 2017 Prob (F-statistic): 6.29e-05 Time: 15:26:12 Log-Likelihood: -17593. No. Observations: 6075 AIC: 3.519e+04 Df Residuals: 6072 BIC: 3.521e+04 Df Model: 2 Covariance Type: nonrobust =================================================================================== coef std err t P>|t| [0.025 0.975] ----------------------------------------------------------------------------------- Intercept 22.1619 0.093 237.366 0.000 21.979 22.345 C(TVHOURS)[T.1] 0.2712 0.137 1.979 0.048 0.003 0.540 C(TVHOURS)[T.2] 0.5985 0.136 4.401 0.000 0.332 0.865 ============================================================================== Omnibus: 1822.675 Durbin-Watson: 1.935 Prob(Omnibus): 0.000 Jarque-Bera (JB): 6241.254 Skew: 1.498 Prob(JB): 0.00 Kurtosis: 6.960 Cond. No. 3.60 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
In [15]:
sub2 = sub1[['BMI', 'TVHOURS']].dropna()
In [18]:
print ('means for BMI by TVHOURS') m1= sub2.groupby('TVHOURS').mean() print (m1)
means for BMI by TVHOURS BMI TVHOURS 0 22.161924 1 22.433088 2 22.760428
From the model results P value of Prob (F-statistic): 6.29e-05
and
F-statistic: 9.690 is obtained from which we can reject the null hypothesis(p<0.05) But the means calculated above does not show significant difference among the groups and does not explain which group is significantly different from others. So we have performed a post hoc test below find out the group which is significantly different.
In [17]:
print ('standard deviations for BMI by TVHOURS') sd1 = sub2.groupby('TVHOURS').std() print (sd1)
standard deviations for BMI by TVHOURS BMI TVHOURS 0 4.025568 1 4.440422 2 4.694750
Tukey’s test has been performed on the groups to see which group is significantly different from others. Below are the results.
In [19]:
mc1 = multi.MultiComparison(sub2['BMI'], sub2['TVHOURS']) res1 = mc1.tukeyhsd() print(res1.summary())
Multiple Comparison of Means - Tukey HSD,FWER=0.05 ============================================ group1 group2 meandiff lower upper reject -------------------------------------------- 0 1 0.2712 -0.05 0.5924 False 0 2 0.5985 0.2797 0.9173 True 1 2 0.3273 -0.0028 0.6574 False --------------------------------------------
Inference: When the ANOVA test has been performed on the data a p value of <0.05 indicated that there is enough evidence to reject the null hypothesis. That means there is relation between the number of Television hours per week to the BMI index of the sample population. But the means were not significantly different to say which group is statistically different from the other. so a posthoc Tukey test has been performed on the data. Above are the results which clearly shows that groups 0 and 2 are statistically different. That means as TV hours increase (bin 2 being the bin with maximum Television hours BMI index is increasing). The young kids who watch Television for 0-7 hours have significantly lower BMI index than kids that watch Television between 30-50 hours a week.
0 notes