#qspr

[qsmptweets]

Official translated tweets : Day 3

Text: Quackity

- Quackity's OXXO.

- Soon a "new" member will be joining to Quesadilla Island.

- The new customs system to cross the wall, for a cost of 10 diamonds.

Text: Luzu

-Luzu places a mine inside Mariana's house as a way to apologize for his death.

- Luzu and Roier make a temporary truce. Luzu reveals that he is the true villain of the QSMP but no one else knows.

- Luzu entered Roier's house, now he knows his house password.

Text: Spreen

- One of his plans is to make turtle races to win bets through them.

- He doesn’t plan on staying behind on building things, and wants to build a mansion to live in.

- Spreen proclaimed a mushroom biome island.

Text: Maximus

- Maximus plans on showing a presentation to all of the members of QSMP! (one of them includes a discussion as to why Vegetta is obsessed with symmetry)

- Quackity told Maximus that he plans to make customs in the hole in the wall.

Text: Vegetta

-Vegetta started with lore about the “Night Magician”. Plans to make a business in which he can sell things others need

-Plans to earn everyone’s trust and create a cult continues

-Discovered that one of the new rules is that he can’t have more than 3 rows of hearts

[anonymous-dentist]

A list of ‘disappearances’ and their canon explanations:

q!Jaiden- all-expense paid Federation work trip

q!Cellbit- kidnapped and brainwashed by the Federation

q!Fit- bro got capybara-d (they are Federation employees)

q!Tazercraft- put in jail by the Federation

q!Felps- popsicle (Federation flavored)

q!Quackity- treading water (Federation flavored)

q!Etoiles- trapped in the Nether (probably by the Federation, let’s be real)

And then there’s:

q!Wilbur- on tour with Lovejoy

q!Missa- went on vacation to Japan

[cychas]

god what is WITH roier and being emotionally attatched to federation members

[frogblast-the-ventcore]

The Quiet Special Purpose Revolver. Using a 10mm piston-cartridge which silently propelled 12 tungsten shot each.

Designed for use in tunnel fighting, common when engaging the Viet Cong.

A verifiable total of 11 were built (some sources state as high as 250, but is not confirmed) by the AAI Corporation.

Made from Smith & Wesson Model 29s, the weapon is essentially a snub-nosed Model 29 with a variety of differences. Frames for the weapon were provided by Smith & Wesson, but were modified to fit a .40 caliber barrel.

Due to a variety of modifications done to the main Model 29 frame along with the cartridges themselves, the QSPRs are noted to be very quiet. The muzzle report was measured at about 110 dB, the equivalent of a suppressed .22 LR firearm.

The design of the proprietary 10mm QSPR ammunition features a steel case containing series of integral retardants, including pistons and a pellet bed which the projectile passes through as it exits the shortened, smooth-bore barrel of the revolver. The shotgun shell like round is capped with a twist-off sealant, creating a hermetically sealed and entirely self contained suppression mechanism.

Only three QSPRs survive today, two in a US Army museum and one in the ATF reference collection.

[doglok]

茶々くんとゲーム #猫 #マンチカン #shorts via YouTube https://www.youtube.com/watch?v=QSPr-VUxhCo

[mciotti63-blog]

presso Hotel Pulitzer Roma https://www.instagram.com/p/CV--Qf-qsPr/?utm_medium=tumblr

[omc-juniperpublishers]

The Application of Some Computing Techniques in the Drug Design-Juniperpublishers

Abstract

Using global and local reactivity descriptors of DFT and MO theory, in this work, we obtained a nice correlation between theoretically computed and experimentally determined drug activities (MIC). This study once again reveals the fundamental statement of theoretical chemistry that "the structure of a molecule determines its electronic wave function which in turn determines many of its physicochemical properties”. It is reasonable to suppose that the biological activity of molecules its potency as a drug for examples will also, often enough, be dependent upon the molecular electronic wave function. It is possible in principle to determine any molecular property that is ultimately dependent upon the molecule's electronic ground state wave function. In practice this can sometimes be achieved using rigorous procedures.

Abbreviations: QSAR: Quantitative Structure Activity Relationship; QC: Quantum-Chemical; EHT: Extended Huckel Theory; CNDO: Complete Neglect of Differential Overlap; INDO: Intermediate Neglect of Differential Overlap; MINDO: Modified Intermediate Neglect of Differential Overlap; MNDO: Modified Neglect of Diatomic Overlap; AM1: Austin Model 1; PM3: Parametric Model 3; RHF: Restricted Hartree-Fock level.

Introduction

Years of cumulative research can result in the development of a clinically useful drug, providing either cures from a particular disease or symptomatic relief form a physiological disorder. A dug, with a diseased pharmacological activity may have associated with some undesirable side effects which limits its' use. Current research reveals that the function of a drug may associate with its structural features. Computational theoretical chemistry is a branch of chemistry that uses theoretical studies to assist in solving chemical problems. It uses the results of theoretical chemistry, incorporated into efficient computer programs, to calculate the structures and properties of molecules and solids. While its results normally complement the information obtained by chemical experiments, it can in some cases predict hitherto unobserved chemical phenomena. It is widely used in the design of new drugs and materials.

Now a day, the synthesis of novel pharmacologically active molecules with reduced toxicity is of prime interest. Recently, QSAR has gained importance in the field of pharmacological sciences [1]. Quantitative structure Activity relationships (QSAR) are predictive tools for a preliminary evaluation of the activity of chemical compounds by using computer-aided models. The computational chemist can assist the experimental chemist or it can challenge the experimental chemist to find entirely new chemical objects.The Hohenberg and Khon theorm based DFT [2-4] provide a major boost to the computational chemistry The performance of DFT method in description of structural, energetic and magnetic molecular properties has been reviewed quite substantially in recent time.

DFT methods are in general capable of generating a variety of isolated molecular properties [5-12]. The commercial exploitation of organic compounds as a medicinal drug for examples is likely to require, at some stage of its development, the determination of biological or chemical activities or properties related to the intended end use of the compound. It is desirable therefore to have at hand relatively straightforward and inexpensive procedures enabling the efficient and accurate prediction of a molecular activity or property especially when its direct measurement by experiment is, for one reason or another, to be avoided if at all possible. The procedures that are conventionally used for indirect determinations of activities make use of molecular “descriptors” which include suitable molecular properties and physical-organic constructs obtained from both experimental and computational sources. Molecular descriptors are ultimately related to molecular structure. Hence the relationships between activities and the descriptors on which they depend are generally known as Quantitative Structure- Activity Relationships (QSARs) or Quantitative Structure- Property Relationships (QSPRs) depending upon whether the property of interest is to be characterized as biological or nonbiological, respectively.

The structure of a molecule determines its electronic wave function which in turn determines many of its physicochemical properties. It is reasonable to suppose that the biological activity of molecules its potency as a drug for examples will also, often enough, be dependent upon the molecular electronic wave function. It is now possible to perform accurate ab initio calculations routinely on molecules of moderate size at reasonable cost. Thus, it would clearly be advantageous to have available a procedure for estimating a molecular activity or property from descriptors which are derived from, and in turn characterize, the electronic wave function of a molecule.

It is possible in principle to determine any molecular property that is ultimately dependent upon the molecule's electronic ground state wave function. In practice this can sometimes be achieved using rigorous procedures. It can, for instance, be achieved for certain properties using quantum-mechanical expectation values. But when rigorous procedures are difficult or virtually impossible then it is necessary to use either a less rigorous model calculation or to use the Quantitative structure- activity relationship or Quantitative structure-property relationship methods.

Quantitative structure-activity relationship (QSAR) techniques increase the probability of success and reduce time and cost involvement in drug discovery process [13,14]. In this work, a correlation between the DFT descriptors and the drug activity of the Benzo[f]quinazolin-1(2H)-ones has been discussed. The aim of the present work is to explore the efficacy of the DFT based descriptors to provide some relationship by which the biological activity of hypothetical molecule can be measure prior to their synthesis. This technique shall reduce the drug discovery coast, time and efforts. In recent year heterocyclic compounds analogues of benzothaizoles and derivatives have attracted strong interest due to their useful biological and pharmacological properties. The chemistry of quinazolinones is interested because of its biological significance. Many of them shows antifungal [15], antibacterial [16], anticancer[17] anti- inflammatory[18] anticonvulsant [19] and antiproliferative activities as well as inhibitory effects for thymidylate synthase and poly-(ADP-ribose) polymerase (PARP) [20]. Quinazolin- 1-one derivatives are also found to be tranquilizer, antiallergic agent, an antiulcer agent and antiasthmatic agent.

Quantum-chemical (QC) calculations are a key element in biological research [21]. When constantly tested for their range of validity QC methods provide a description of how molecules interact and form their three-dimensional shape, which in turn determines molecular function. They can aid the formulation of hypotheses that provide the connecting link between experimentally determined structures and biological function. QC calculations can be used to understand enzyme mechanisms, hydrogen bonding, polarization effects, spectra, ligand binding and other fundamental processes both in normal and aberrant biological contexts. The power of parallel computing and progress in computer algorithms are enlarging the domain of QC applications to ever more realistic models of biological macromolecules.

The key insight of chemistry is the relationship between molecular structure and molecular function. We use the details of molecular structure to predict the properties of molecules. Medicinal chemistry is a particularly glaring example of our use of structure-function relationships. There is a tremendous need to be able to quickly design new drugs for curing human disease. The rapid prediction of the activities of compounds for use as drugs and the discovery of new compounds is an important goal. Quantitative Structure Activity Relationships, or QSAR [22] enables us to predict the properties of compounds and are a quantitative expression of structure-function relationships. QSAR has been responsible for the rapid development of many new drugs.

An example of a QSAR study is the narcotic activity of esters, alcohols, ketones, and ethers with tadpole. In this study various organic compounds were added to water with swimming tadpoles. The swimming speed of the tadpoles was observed and the amount of the compound that was necessary to slow the tadpoles swimming was determined. A very effective compound has a very low concentration for the production of the desired effect. In QSAR studies we often like to have the more effective compounds have a higher "activity,” not a lower. Therefore, it is very common to transform the concentration for a desired effect, C, to an activity by:

A = log(1/C) (1)

The log(1/C) value increases with compound efficacy

The genesis of QSAR is from physical organic chemistry and linear free energy relationships. The first such studies were done by L. P. Hammett [23]. His goal was to uncover the effects of electronic structure on organic reactivity. A short discussion of his work will be instructive as we start to understand the foundations of QSAR. Hammett's first studies were to understand the effect of electron withdrawing and donating groups on the pKa's of substituted benzoic acids, Hammett first wanted to develop a descriptor that described inductive substituent effects. He compared the log Ka for a variety of substituted benzoic acids with the log KaH for unsubstitued benzoic acid to define the substituent constant σ.

σ = log Ka - log KaH (2)

σ the Hammett constants for meta and para substituents. He then postulated that other properties, other than acidity, would be likewise effected by the same substituent effects, and that these other properties would follow the relationship

log (property) = ρ σ + cst (3)

In other words, the expected function was a linear relationship with the ρ inductive constant.

Hammett obtained the equation from the relationship between Gibbs free energy and the equilibrium constant for a reaction,

Δ rG = - RT ln Keq (4)

Semi-empirical methods can be used to calculate quantum chemical descriptors [24]. A number of semi empirical methods have been developed over the last several decades. To name but some of the most popular extended Huckel theory (EHT) [25], complete neglect of differential overlap (CNDO) [26] intermediate neglect of differential overlap (lNDO),[27]modified INDO- (MINDO), [28]modified neglect of diatomic overlap (MNDO),[29] Austin model 1 (AM1), ),[30] and parametric model 3 (PM3) [31].

The density functional theoretical parameters

Given the electron density function p(r) in a chemical system (atom or molecule) and the energy functional E(p), the chemical potential, μ of that system having N number of electrons in equilibrium has been defined as the derivative of the energy with respect to the number of electrons at fixed molecular geometry

The chemical potential [32], μ, is given by

μ= [δE(p) / δp] (5)

The differential definition more appropriate to atomic system is

μ = [∂E / ∂N]v (6)

Then following Iczkowski and Margrave [33], Parr and Pearson [34] defined the electro negativity as the additive inverse of the chemical potential-

χ = - μ (7)

or, χ = - [∂E/∂N] v (8)

and the absolute hardness, η, as

η = 1/2[∂μ/∂N] v = 1/2[∂2E/∂N2)] v (9)

The softness is defined as inverse of hardness (S=1/η).

Parr and Pearson [34] invoking the calculus of finite difference approximation suggested the approximate and operational formulae of electro negativity and hardness as under

χ = (I + A)/2 (10)

η = (I - A)/2 (11)

where l and A are the first ionization potential and electron affinity of the chemical species. Pearson [35] proceeded further to evaluate I and A in terms of orbital energies of the highest occupied molecular orbital, HOMO and the lowest unoccupied molecular orbital, LUMO as

χ = (€HOMO -€LUMO)/2 (12)

η = (-€HOMO + -€LUMO)/2 (13)

The electrophilicity, w is a descriptor of reactivity that allows a quantitative classification of the global electrophilic nature of a molecule within a relative scale. Parr et al. [36] suggested that electro negativity squared divided by hardness measures the electrophilic power of a ligand its prosperity to "soak up” electrons.

Thus,

ω = μ2/2η (14)

It is further anticipated that electrophilicity,w should be related to electron affinity, because both w and electron affinity measures capacity of an agent to accept electrons. Electron affinity reflect capability of an agent to accept only one electron from the environment, whereas electrophilicity index measures the energy lowering of a ligand due to maximal electron flow between the donor and acceptor The electron flows may be either less or more than one. Thus the electrophilicity index provides the direct relationship between the rates of reaction and the electrophilic power of the inhibitors [37].

Fukui functions play a prominent role in the field known as conceptual Density Functional Theory (DFT). Parr and Yang [38] based on the original ideas of Fukui [39], introduced fukui function which reflect the response of a molecular system towards a change in the number of electrons (Ne) of the molecular system under consideration .The fukui functions is a measure of local reactivity and defined as:

f (r) = ( ∂ ρ (r) /∂N )v (15)

where ρ(r) is the electron density.

Parr et al. [38] gave us the statement "the preferred direction is the one with largest f(r) at the direction side" and their firm prediction was -

Governing electrophilic attack f- (r)= [ ∂ ρ (r) / ∂N]- v (16)

Governing nuclophilic attack f+ (r)= [ ∂ ρ (r) / ∂N] +v (17)

Governing nutral attack f 0(r)= [ ∂ ρ (r) / ∂N] 0v (18)

These three cases have μs> μr, μs< μr and μs~ μ'r.

A "frozen core" approximation reveals dρ = dρvalue in each case and therefore governing electrophilic attack, f- (r) ≈ ρ (HOMO) (r) (19 ),

governing nuclophilic attack, f+(r) ≈ ρ (LUMO) (r) (20 ),

and governing neutral attack, f 0(r) ≈ 1/2[ρ (HOMO) (r) + ρ (LUMO) (r)] (21).

Go to

Method of Computation

We have used semi-empirical computational procedure, AM1 [31] to compute the orbital energies (HOMO, LUMO). Side by side we have also adopted a sophisticated ab-initio quantum chemical calculation procedure to compute the orbital energies (HOMO, LUMO). To be more specific, the planar structure of each of the substituted biphenyls was drown on the programme ArgusLab4.0.1[40] and geometry optimization was carried out at the restricted Hartree-Fock level (RHF) using STO-3G minimal basis set to compute the orbital energies (HOMO, LUMO) using AM1 procedure[31]. The ab-initio values are obtained when geometry optimization of the planar structure of each of the substituted biphenyls were carried out at restricted HartreeFock level (RHF) using STO-3G minimal basis set on the Hyper Chem 8.06 software [41].

The Ionization energies and electron affinities are calculated using the Koopmans theorem. The hardness value was calculated using Parr and Pearson method [34]. The electrophilicity index was calculated using the Parr et al's formula [36]. HOMO and LUMO Eigen functions obtained in the AM1 calculations were used to compute the fukui functions using Parr et al formulae [38].

Results and Discussion

A look on the Tables 1a &1b reveal that, in both computational procedure-first principle and AM1, the ionization energy is maximum in the case of chloro substituted Benzo[f]quinazolin- 1(2H)-one and it is minimum in case of Benzo[f]quinazolin- 1(2H)-one. Further scrutiny of the table reveals that the electron affinity is maximum for NH2 substituted Benzo[f]quinazolin- 1(2H)-one.and minimum for Benzo[f]quinazolin-1(2H)-one The electro negativity is maximum for Cl substituted Benzo[f] quinazolin-1(2H)-one and minimum for OH Benzo[f]quinazolin- 1(2H)-one. The hardness is maximum for Cl substituted and minimum f Benzo[f]quinazolin-1(2H)-one or OH substituted. The chemical potential is maximum for OH substituted Benzo[f] quinazolin-1(2H)-one Benzo[f]quinazolin-1(2H)-one.andminimum for H Benzo[f]quinazolin-1(2H)-one.

But we have surprisingly noted that the electro negativity value of all compounds studied by first principle on the minimal basis set STO-3G is negative. These do not agree with our normal experiences. We have thus adopted semi-empirical AM1 calculation on the same compounds. The semi-empirical results are discussed on the foregoing sections.

A look on Table 2 reveals that the centre 2C has the maximum f+ value and the centre12N has the minimum f+ value. Also it is found that the centrellC has the maximum f- value and the centre 15O has the minimum f- value in case of Benzo[f]quinazolin-1(2H)-one. A look on Table 3 reveals that the centre 4C has the maximum f+ value and the centre...17C has the minimum f+ value. Also it is found that the centre 3C has the maximum f- value and the centre 6C has the minimum f-value in case of Cl substitution Benzo[f]quinazolin-1(2H)-one.

A look on Table 4 reveals that the centre 17N has the maximum f+ value and the centre 11C has the minimum f+ value. Also it is found that the centre 3C has the maximum f- value and the centre 1C has the minimum f-value in case of NH2 substitution Benzo[f]quinazolin-1(2H)-one. A look on Table 5 reveals that the centre 2C has the maximum f+ value and the centre 8C has the minimum f+ value. Also it is found that the centre 3C has the maximum f- value and the centre 1C has the minimum f-value in case of CH3 substitution Benzo[f]quinazolin-1(2H)-one .

A deeper look on the Tables 3-6 reveals that the fukui functions on the different atoms of the molecules studied depends upon the substituents. The nucleophilic fukui functions of the 12 N atom varies in the following order- Benzo[f]quinazolin- 1(2H)-one OH->Cl>CH3>H>NH2 Benzo[f]quinazolin-1(2H)-one .The electrophilic fukui function of the 12 N atom varies in the following order- H>NH2l>CH3>Cl>OH Benzo[f]quinazolin-1(2H)- one .The nucleophilic fukui function of the 14 N atom varies in the following order- Cl>CH3>OH>H>NH2 Benzo[f]quinazolin- 1(2H)-one. The electrophilic fukui function of the 14 N atom varies in the following order- H>Cl>CH3>OH>NH2 Benzo[f] quinazolin-1(2H)-one. The nucleophilic fukui function on the 15 O atom varies in the following order-OH-Benzo[f]quinazolin- 1(2H)-one>Cl-Benzo[f]quinazolin-1(2H)-one>CH3- Benzo[f] quinazolin-1(2H)-one >H- Benzo[f]quinazolin-1(2H)-one>NH2- Benzo[f]quinazolin-1(2H)-one.

The electrophilic fukui function on the 15 O atom varies in the following order-CH3 Benzo[f]quinazolin-1(2H)-one >Cl Benzo[f]quinazolin-1(2H)-one >OH Benzo[f]quinazolin-1(2H)- one >NH2>H Benzo[f]quinazolin-1(2H)-one. The nucleophilic fukui function on the 16N atom varies in the following order-

Cl- Benzo[f]quinazolin-1(2H)-one> Benzo[f]quinazolin- 1(2H)-one>OH- Benzo[f]quinazolin-1(2H)-one >CH3- Benzo[f] quinazolin-1(2H)-one> NH2- Benzo[f]quinazolin-1(2H)-one. The electrophilic fukui function on the 16N atom varies in the following order-NH2- Benzo[f]quinazolin-1(2H)-one>OH- Benzo[f]quinazolin-1(2H)-one>CH3 Benzo[f]quinazolin-1(2H)- one >Cl- Benzo[f]quinazolin-1(2H)-one> Benzo[f]quinazolin- 1(2H)-one.

We have found a linear correlation between the global reactivity parameters of conceptual density functional theory and their drug activities.

We have correlated the global reactivity parameters of conceptual density functional theory with the drug activities of the Benzo[f]quinazolin-1(2H)-ones. We have found excellent correlation between the global hardness of the molecules and their drug activity.

Our suggested ansatz for the drug activity are‑

Drug Activity = ‐0.1289rηab‐initio + 1.1378 (22]

Drug Activity =‐0.1919 χab‐initio +0.3446 (23)

Drug Activity = 0.1919 μab-initio +.3446 (24)

Drug Activity = 0.081ωab‐initio + 1.3171 (25)

Drug Activity = 0.0086Sab‐initio + 0.3268 (26)

And using AM1 reactivity parameters

Drug Activity = ‐6.00386ηAM1 + 1.0789 (2 7)

Drug Activity =2.2924 χAM1 +0.1481 (28)

Drug Activity = ‐2.2924 μAM1 ‐0.1481 (29)

Drug Activity = 0.0894ωAM1 + 0.2604 (30)

Drug Activity = 0.0688SAM1 + 1.0789 (31)

We have computed the drug activity of the Benzo[f] quinazolin-1(2H)-ones using the above ansatz 1,2 and 4 and 6,7 and 9 and presented them in Tables 6-12. As the chemical potential is the negative counterpart of electro negativity and the softness is the inverse of hardness only, we have not considered them for computing the activity value. A deep scrutiny of the Tables 6-12 reveal that the theoretical activity value correlate well with the experimental values. In the case of hardness, this correlation is the best among the reactivity parameters in both ab-initio and AM1 computed results. We have drown Figures 1 & 2 to explore the correlation between theoretical computed and experimentally determined drug activity value of the Benzo[f] quinazolin-1(2H)-one using ab-initio and semi empirical hardness values respectively. From Figures 1 & 2 we can see that the activity data of the four compound correlate excellently with the experimental values. In the case of AM1 hardness data excellent correlation found in two values and other values fairly correlate with the experimental data.

Conclusion

Using global and local reactivity descriptors of DFT and MO theory, we have found a nice correlation between theoretically computed and experimentally determined drug activities (MIC). The fukui functions and local softness's at different sites changes with the change in substituents. This study once again reveals the fundamental statement of theoretical chemistry that "the structure of a molecule determines its electronic wave function which in turn determines many of its physicochemical properties”. It is reasonable to suppose that the biological activity of molecules its potency as a drug for examples will also, often enough, be dependent upon the molecular electronic wave function. It is possible in principle to determine any molecular property that is ultimately dependent upon the molecule's electronic ground state wave function. In practice this can sometimes be achieved using rigorous procedures.

To know more about Journal of chemistry,

Click here: https://juniperpublishers.com/omcij/index.php

To know more abour juniper Publishers,

click here: https://juniperpublishers.com/index.php

[nonbinaryskulls]

@qspr I fuck with this

[qsmptweets]

Official translated tweets : Day 6

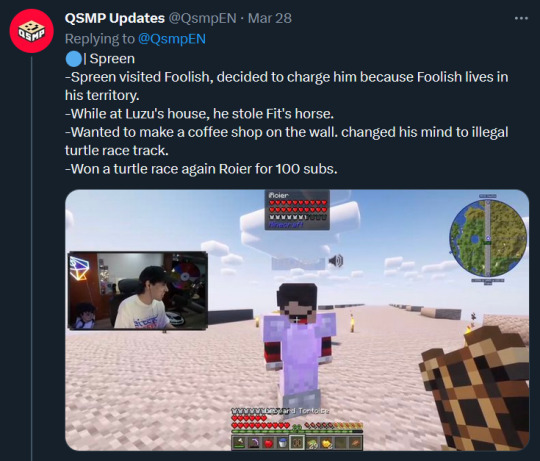
Text: Spreen

-Spreen visited Foolish, decided to charge him because Foolish lives in his territory.

-While at Luzu's house, he stole Fit's horse.

-Wanted to make a coffee shop on the wall. changed his mind to illegal turtle race track.

-Won a turtle race again Roier for 100 subs.

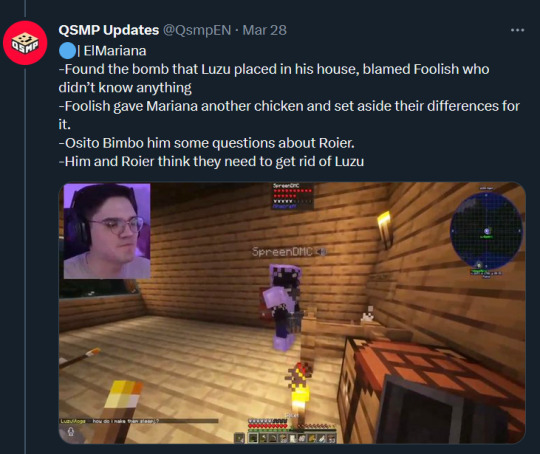
Text: ElMariana

-Found the bomb that Luzu placed in his house, blamed Foolish who didn’t know anything

-Foolish gave Mariana another chicken and set aside their differences for it.

-Osito Bimbo him some questions about Roier.

-Him and Roier think they need to get rid of Luzu

Text: Vegetta

-Him and Luzu met up and talked about the materials Luzu found while exploring.

-He removed a sign Foolish left for him on accident that was hanging on his tree.

-He’s looking for members for his sect “The Wise”.

-He left a great present for Foolish!

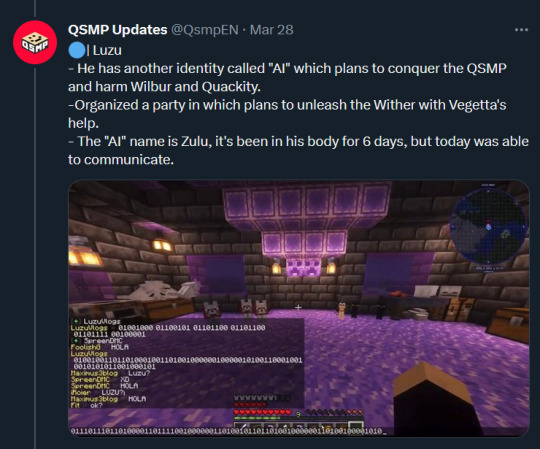
Text: Luzu

- He has another identity called "AI" which plans to conquer the QSMP and harm Wilbur and Quackity.

-Organized a party in which plans to unleash the Wither with Vegetta's help.

- The "AI" name is Zulu, it's been in his body for 6 days, but today was able to communicate.

Text: Zulu

-Communicates in binary code, and asked questions about the server and the people on it.

-He doesn't understand feelings and basic human interactions.

-Spreen is not his friend, he tried to kill Quackity but was pursued he's his friend.

-The world is the "big room".

Text: Maximus

-Adopted Zulu (Luzu AI) with Foolish

-Osito Bimbo asked him about Luzu, said that he doesn't trust in him

-Devil Rubius told him to put fake lava on Foolish's build

-Maxo gave him a counter offer to break the windows of Luzu's house, he did.

-Rubius killed his wolf

Text: Roier

-Roier and Quackity are building the Oxxo

-Osito Bimbo asked him about -Mariana, gave Roier a toy that makes bubbles.

-Roier and Spreen tried to kidnap Osito Bimbo.

-He and Quackity made the decision to remodel Mariana’s house.

-Roier will start building his taqueria.

[commentsense888]

Man cave not found. Found in /r/gaming by Qspr https://www.reddit.com/r/ProgrammerHumor/comments/6rjh15/man_cave_not_found_found_in_rgaming/?utm_source=ifttt

[lupinepublishers]

On the Second Harmonic Index of Titania Nanotubes by Mohammad Reza Farahani in #DDIPIJ in #Lupinepublishers

Topological indices which are graph invariants derived from molecular graphs of molecules are used in QSPR researches for modeling physicochemical properties of molecules. Topological indices are important tools for determining the underlying topology of a molecule in view of theoretical chemistry. The second harmonic index has been defined recently. In this study we compute the second harmonic index of Titania nanotubes. 

https://www.lupinepublishers.com/drug-designing-journal/fulltext/DDIPIJ.MS.ID.000102.php

[nonbinaryskulls]

@whattatadotoday @qspr

Boyfriend: *lighting romantic candles and spreading rose petals on the bed*

Me: oh dang what spell are we gonna be doing

[omc-juniperpublishers]

Polarizability Study of Fullerene Nano- g Structures C20 to C300 by Using Monopole-Dipole s Interactions Theorem-JuniperPublishers

Journal of Chemistry-JuniperPublishers

Abstract

Since the discovery of fullerenes (Cn), one of the main classes of carbon compounds, the unusual structures and physiochemical properties of these molecules have been discovered, and many potential applications and physicochemical properties have been introduced. Up to now, various empty carbon fullerenes with different numbers "n,” such as C20 through C300 (like C60, C70, C76, C82,..., C300) have been obtained. The linear uniform field electric dipole polarizability tensors of 46 fullerenes in the range C20 through C240 were calculated by the Atom MonopoleDipole Interaction (AMDI) theory, using the monopole and dipole polarizabilities of the carbon atom found previously to fit polarizability tensors of aromatic hydrocarbons. The structures are taken to be those predicted by molecular dynamics energy optimization. The isotropic mean polarizabilities calculated for C60 and C70 are comparable to experimental data from solid film studies and to quantum mechanical calculations. Topological indices are digital values that are assigned based on chemical composition. These values are purported to correlate chemical structures with various chemical and physical properties. They have been successfully used to construct effective and useful mathematical methods to establish clear relationships between structural data and the physical properties of these materials. In this study were extended the calculation of the parameters concern to atom monopole-dipole moment such as Ellipsoid (αl to α3 and α), AMDI (Atom monopole-dipole interaction theory; αl to α3 and ā) and semi-axes a,b,c of a thin ellipsoidal shell of uniform thickness (in Å, ABC al to α3) by QSAR for C20 through C300 .

Keywords: Fullerenes; Polarizability; Amdi Theory; Ellipsoid; Semi-Axes Thin Ellipsoidal Shell

Abbreviations: AMDI: Atom Monopole Dipole Interaction; FC: Ferrocene; TI: Topological Indices; Atom Monopole Dipole Interaction (AMDI); TI: Topological Indices; MLR: Modeling; MLR: Modeling Both Linear

Introduction

The electrochemical properties of the fullerene C60 have been studied since the early 1990s, when these materials became available in macroscopic quantities (for a review see [1]). [1-3] in 1990, have shown that C60 is electrochemically reducible in the CH2Cl2 medium to C60- and C602-. In 1992, have cathodically reduced both C60 in six reversible one-electron steps for -0.97 vs. Fc/Fc+ (FC=Ferrocene). This fact, along with the absence of anodic electrochemistry of fullerenes, matches the electronic structure of fullerenes: the LUMO of C60 can accept up to six electrons to form C606-, but the position of the HOMO does not allow for hole-doping under the usual electrochemical conditions. In 1991, Bard et al. [4-8] first reported on irreversible electrochemical and structural reorganization of solid fullerenes in acetonitrile medium. Dunsch et al. [5] have upgraded the experimental conditions by investigating highly organized C60 films on HOPG in aqueous medium. The reduction of such films manifested itself by re-structuring into conductive nanoclusters of ~102 nm in diameter [5-9].

The linear uniform field electric dipole polarizability tensors of 46 fullerenes in the range C20 through C240 are calculated by the Olson Sundberg Atom Monopole-Dipole Interaction (AMDI) theory, using the monopole and dipole polarizabilities of the carbon atom found previously to fit polarizability tensors of aromatic hydrocarbons. The structures are taken to be those predicted by Zhang and co-workers by molecular dynamics energy optimization. The isotropic mean polarizabilities calculated for C60 and C70 are comparable to experimental data from solid film studies and to quantum mechanical calculations. Polarizability tensors are also calculated for conducting ellipsoidal shells which have the same moment of inertia tensor as the corresponding fullerenes. These are substantially smaller than the AMDI polarizabilities for the smaller fullerenes, but the two calculations tend to converge for the larger molecules. [7-15]

Graph theory has been found to be a useful tool in assessing the QSAR (Quantitative Structure Activity Relationship) and QSPR (Quantitative Structure Property Relationship). Numerous studies in the above areas have also used what are called Topological Indices (TI). It is important to use effective mathematical methods to make good correlations between several data properties of chemicals. Numerous studies have been performed related to the above mentioned fields by using the so-called Topological Indices (TI). The numbers of carbon atoms at the structures of the fullerenes were utilized here [7-15].

In this study were extended the calculation of the parameters concern to atom monopole-dipole moment such as Ellipsoid (α1 to α3 and ā), AMDI (Atom monopole-dipole interaction theory; al to α3 and ā) and semi-axes a,b,c of a thin ellipsoidal shell of uniform thickness (in Å, ABC α1 to α3) by QSAR for C20 through C300 .

Graphs And Mathematical Method

All graphing operations were performed using the Microsoft Office Excel 2003 program. The numbers of carbon atoms at the structures of the fullerenes Cn were utilized to make the relationship and calculate the Ellipsoid, AMDI and thin ellipsoidal shell of uniform thickness. For Modeling, Both Linear (MLR) and nonlinear (ANN) models were used in this study.

Discussion

The polarizabilities of the ellipoids are simply correlated with their geometry, as can be seen from the fact that the principal polarizabilities are approximately proportional to the lengths of the corresponding axes. To some extent this holds for the AMDI model as well, but for the smaller members of the series there are cases where the principal polarizabilities are not in the same ratio as the axes. His is apparently because the atom dipole contribution, which is not simply related to the axis lengths, is relatively larger for the smaller members. A further measure of the correspondence between the molecules and the ellipsoids is found in the comparison of the principal polarizability axes found by the AMDI theory with the principal geometric axes of the ellipsoids. Where the three semi-axes are distinct, the axes directions are the same to within a few tenths of a degree. The numbers of carbon atoms at the structures of the fullerenes Cn were utilized and extended the calculation of the parameters concern to atom monopole-dipole moment such as Ellipsoid (α1to α3 and ā), AMDI (Atom monopole-dipole interaction theory;α1 to α3 and ā) and semi-axes a,b,c of a thin ellipsoidal shell ofuniform thickness (in Å, ABC al to α3) by QSAR for C20 through C300.

To know more about Journal of chemistry,

Click here: https://juniperpublishers.com/omcij/index.php

To know more abour juniper Publishers,

click here: https://juniperpublishers.com/index.php

[qsmptweets]

Actualizaciones en Spreen : Día 9

Text: Actualizaciones de Spreen, QSMP Día 9!

Text: Spreen fue amenazado por Rubius de no decir nada sobre él o le destruirá la casa

[video]

Text: Spreen dice que las personas que le caen mejor son Roier y Missa, y que no se lleva bien con Fit

[video]

Text: Spreen mató al gato de Roier...

[video]

Text: Spreen fue a pedirle disculpas a Roier

[video]

Text: Spreen logró el waterdrop!

[video]

Text: Spreen se confesó con Rubius sobre sus pecados

[video]

Text: Spreen cerró directo!

[video]

[tejas-e-store-blog]

*Kids Footwears Vol-2 IS00015-BR-BLU-MFN (Code: VIRZ)* ₹ 537 _Dispatches in 2–3 days_ FREE COD ✅ Package Contains:- Footwear Material :- Cotton Color :- Multi-color Product Dimensions (L XB X H) :- 16 X 8 X16 Size :- 13 EU *Kids Footwears Vol-2 IS00012-2020-VLRC-BLU13 (Code: LYED)* ₹ 537 _Dispatches in 2–3 days_ FREE COD ✅ Package Contains:- Footwear Material :- Cotton Color :- Blue Product Dimensions (L XB X H) :- 16 X 8 X16 Size :- 13 EU *Kids Footwears Vol-2 IS00014-VLCR-GRY (Code: KNVP)* ₹ 537 _Dispatches in 2–3 days_ FREE COD ✅ Package Contains:- Footwear Material :- Cotton Color :- Multi-color Product Dimensions (L XB X H) :- 16 X 8 X16 Size :- 13 EU *Kids Footwears Vol-2 IS00018-VLCR-DRK-PNK (Code: VCZY)* ₹ 537 _Dispatches in 2–3 days_ FREE COD ✅ Package Contains:- Footwear Material :- Cotton Color :- Blue Product Dimensions (L XB X H) :- 16 X 8 X 16 Size :- 13 EU *Kids Footwears Vol-2 IS00013-GL-0-9-BLU 13 (Code: BDPV)* ₹ 537 _Dispatches in 2–3 days_ FREE COD ✅ Package Contains:- Footwear Material :- Cotton Color :- Black Product Dimensions (L XB X H) :- 16 X 8 X16 Size :- 13 EU *Kids Footwears Vol-2 IS00016-LCS-BLK (Code: QSPR)* ₹ 537 _Dispatches in 2–3 days_ FREE COD ✅ Package Contains:- Footwear Material :- Cotton Color :- Pink Product Dimensions (L XB X H) :- 16 X 8 X16 Size :- 13 EU *Kids Footwears Vol-2 IS00019-LCS GREEN (Code: CWZX)* ₹ 537 _Dispatches in 2–3 days_ FREE COD ✅ Package Contains:- Footwear Material :- Cotton Color :- Brown Product Dimensions (L XB X H) :- 16 X 8 X16 Size :- 13 EU *Kids Footwears Vol-2 IS00020-VLC-PINK (Code: YUFP)* ₹ 537 _Dispatches in 2–3 days_ FREE COD ✅ Package Contains:- Footwear Material :- Cotton Color :- Blue Product Dimensions (L XB X H) :- 16 X 8 X16 Size :- 13 EU *Kids Footwears Vol-2 IS00017-VLCR-CAT-BLK (Code: GKHM)* ₹ 537 _Dispatches in 2–3 days_ FREE COD ✅ Package Contains:- Footwear Material :- Cotton Color :- Black Product Dimensions (L X B X H) :- 16 X 8 X 16 Size :- 13 EU Get them here : https://www.shop101.com/Tejase-store/shares/8516888665?15chpg