#i can't set the number of loops to 0 or -1 or anything like that

[smellslikebot]

i decided making 3ds themes with custom music Sucks because the program you're supposed to use to convert the music also makes you enter a finite number of times for the loop region to loop, and it also does not honor that number at all. it ALWAYS loops once and then restarts the song from the beginning. and for some reason nobody has reported this as an issue so i'm left wondering if i'm just missing something obvious

[klavierpanda]

Tell me about math's. Anything. I'm so curious

Okay! I will tell you about one way we can test for holes in a topological space!

I will first clarify what I mean by a loop because it's important to be precise and they are the star of this show! A loop in a topological space X is continuous map from the interval [0,1] to X which starts and ends at the same point.

To motivate our test we shall look at two examples!

First imagine a plane (ℝ²). Intuitively this has no holes. If we consider a loop in the plane we can imagine shrinking this loops down to a point. This is sort of like placing a rubber band on a table and squishing it down as close as you can (except rubber bands have a physical limitation. Even if you can keep squishing it, you'd eventually make a black hole). It's important to point out that the loop lives in the space rather than on top of it like a rubber band on a table.

Now imagine an annulus (see picture)

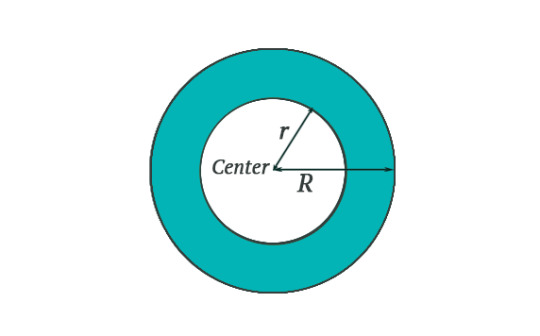
This obviously has a hole in the middle. Now we can consider loops in an annulus. We can think about two kinds of loops!

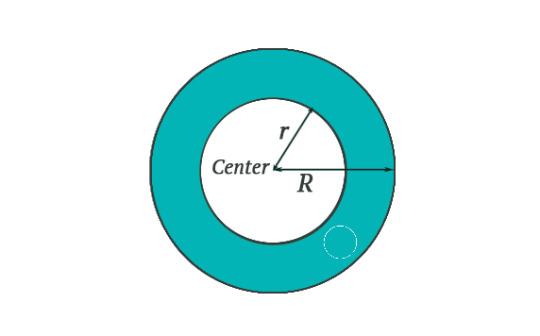
The first kind doesn't go around the hole and we can still shrink these to a point. The other kind goes around the hole and when we try to shrink it, it snags on the hole.

So the idea is that we can find the presence of a hole in a space by shrinking loops to see whether they can be made into a point or not. We can adapt the rubber band analogy by adding the extra rule that the rubber band must always touch the table at all its points. So if we were to cut a hole into the table, we would no longer be able to shrink the rubber band.

Let's try another example! We shall look at a torus. This is the surface of a ring doughnut (that is, it doesn't have anything on this inside).

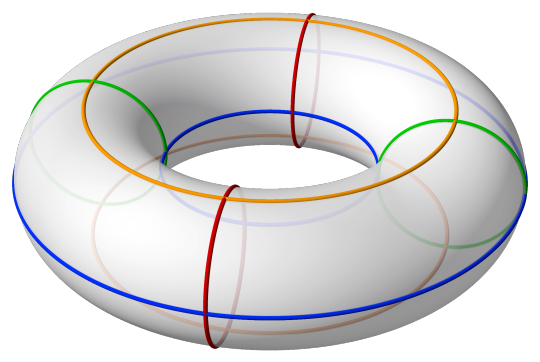
First consider the red and green loops. All we can do with these is move them around the tube. We can't shrink them. Similar, we can't shrink the orange and blue loops. We also can't deform a blue/orange loop into a green/red loop and vice versa! So a torus must have some holes!

One thing that might seem weird is that holes can have different dimensions! The part of our space which bounds the hole can have a different dimension which means the hole is fundamentally different. In this context the dimension of a space is to do with what the space locally looks like. That is, if you were to zoom in closely the space would sorta look like a flat Euclidean space, i.e. a line or a plane or 3D space etc. For example, the torus is 2 dimensional since locally it looks like a plane. A circle is 1 dimensional since locally it looks like a line. Another way to think of this is how many different independent directions could you walk if you lived in that space. Another example is the sphere, think the surface of the earth. This is two dimensional because we only require two numbers to describe positions on it!

The reason I bring this up is our test can't always detect the presence of holes! This is because our test is great at picking up on 1 dimensional holes, but it doesn't always detect higher dimensional holes. A good example here is the sphere. We can always shrink a loop on a sphere but it's fairly easy to see that the sphere bounds a region that isn't a part of the sphere itself. There is a 2 dimensional hole in the sphere.

One more neat thing we can do with loops in spaces is we can use them to define a nice algebraic structure! By algebraic structure, I mean anything that involves a set and an operation between elements of that set which produces another element of that set. An example of this is the integers with addition. We can add two integers to get another integer. The integers have some nice properties. There is an element 0 such that 0+n=n+0=n. We can also take inverses, i.e. we for any integer n there exists another integer m such that n+m=0. We also have a property called associativity. This is the rule that says (n+m)+k=n+(m+k). This makes the integers what's called a group!

We can make a group using loops in a topological space! We first pick a basepoint which every loop will start at. Then we define out operations on the loops to be concatenation. That is, given two loops f and g, we define f*g to be the loop we get by first going around f then going around g. We also have the added rule that we consider loops that can be deformed into each other to be the same. The identity element is the constant loop, i.e. the loop e such that e(t)=x for all values of t, where x is our basepoint. The group that we get is called the fundamental group (kinda pompous but it really is important!).

We can see an example of this using the annulus from earlier! We can consider an anticlockwise loop around the hole to correspond to the number 1. We can get successive positive numbers by going around this loop the right number of times! We get negative numbers using clockwise loops! (Equally we can make clockwise loops correspond to positive numbers and anticlockwise to negative numbers).

The fundamental group turns out to be a very powerful tool! It turns out that if topological spaces have different fundamental groups they can't be the same space (strictly speaking, they can't be homeomorphic or even homotopy equivalent). And we can prove some useful results using fundamental groups too!

This is all formalised in the area of maths called Algebraic Topology (the area I hope to do research in!). Making this all rigorous is no easy task (I have written a few formal posts about it on my maths blog!)

This was a lot longer than I had planned originally haha. I've been writing for about an hour and a half. I hope you find it interesting!

[4denthusiast]

Couldn't you just use basically the same construction again for generalized homotopies? The main issue is just that it's a little fiddly to deal with homotopies between generalized paths whose lengths can differ. Define a generalized homotopy between generalized paths f and g to be a function from open covers 𝒰 to families (U_a,b)_{1≤a,b≤m}, where U_a,b ∈𝒰 and it overlaps both U_a,b+1 and U_a+1,b, the size m is ≥ the lengths of f(𝒰) and g(𝒰), U_1,n =f(𝒰)_n and U_m,n = g(𝒰)_n (where indexing a sequence with an index greater than its length is assumed to give its last element again), x ∈U_n,1 and y ∈U_n,m. This is clearly an equivalence relation. You can turn homotopies into generalized homotopies the same way you can paths. I'm pretty sure composing and inverting generalized paths is compatible with these generalized homotopies so the equivalent of the fundamental group can be constructed. These fundamental groups do not depend on the chosen basis point (for connected spaces), as desired.

The fundamental group thus defined is not very well behaved, because a single generalized path can just go completely different ways depending on what open cover it's given. The generalized fundamental group of the circle is probably something like ℤ^{open covers of S1}. I'll get to how to fix this later.

For this reason, we can't prove the generalized fundamental group of the Warsaw circle, as defined in this way, is the integers (as would be expected), but here's a sketch of a proof that that group at least has a surjective morphism to the integers.

Fix some open cover 𝒰 of the Warsaw circle, which can be arbitrary so long as it contains three open sets A,B,C,D which overlap in a chain (and don't overlap anything else in 𝒰 except at A and D), and and a point t outside of A,B,C, and D. Define the winding number of a generalized path f from t to t to be the number of times f(𝒰) passes along A->B->C->D, minus the number of times is passes along D->C->B->A. If two generalized paths f and g have a homotopy H, then the sequence (H(𝒰)_a,n)_a maintains its winding number as we increase n from 1 to the length of H(𝒰), therefore f and g have the same winding number. Winding number is additive for path composition and 0 for the identity path, and it's pretty obvious that there's a path of winding number 1 (because the Warsaw circle with B and C removed is connected, and therefore generalized-path-connected), therefore winding number is a surjective morphism from the generalized fundamental group of this space to the integers, QED.

I thought maybe you could make the generalized fundamental groups work properly by adding an additional restriction to the generalized paths, that for any two open covers 𝒰 and 𝒱, a generalized path f from x to y must have a sequence of sequences passing from f(𝒰) to f(𝒱), with similar restrictions to those used for generalized homotopies but in addition every open set used must appear in the original sequences f(𝒰) and f(𝒱) (so you can't wander off to other regions of the space). This doesn't actually work though, because it would prevent the generalized paths from being general enough. Such a path crossing the topologist's sine curve would still need an infinite number of wiggles even for finite sized open covers.

Another thought on how to fix the generalized fundamental groups: Define the fundamental group of the non-empty connected space S at the cover 𝒰 , π1(S,𝒰), to be the set of equivalence classes under homotopy of paths through the graph of overlaps of 𝒰 (where the homotopies can pass over loops of length up to perhaps 3 or 4). If each element of 𝒰 is a subset of an element of 𝒱, this gives an obvious morphism from π1(S,𝒰) to π1(S,𝒱), and these define a functor from the partial order of open covers of S under refinement to the category of groups. If we then take the limit of this functor, maybe we get something sensible? The partial order is a downward directed set so I don't think we'd get loads of separate copies of essentially the same topological loops in the group at least, like in the previous construction. I intuitively feel like this notion of generalized fundamental group should give ℤ for both the Warsaw circle and the normal circle, and I know generally there's a reasonably simple construction for a morphism from the actual fundamental group into this generalized fundamental group, which is likely an isomorphism for sufficiently well-behaved spaces (manifolds and stuff) (local path-connectedness might be the relevant criterion), but that seems like it would be a lot of work to prove any of that. Basically the same construction should work for the higher homotopy groups too.

Quite likely if what I have just described actually works right, it has some standard name already, but if so I don't know it.

Okay how about this: a generalized path between points x and y of a topological space X is a function P that assigns to every open cover 𝒰 of X a finite sequence (U₁,...,Uₙ) (call it a connecting sequence) of 𝒰-sets such that x ∈ U₁, y ∈ Uₙ, and for all 1 ≤ k < n we have that Uₖ ∩ Uₖ₊₁ ≠ ∅. Such a function exists if and only if x and y are contained in the same connected component of X.

To see this, note first that if there are disjoint open sets U, U' such that U ∪ U' = X and x ∈ U, y ∈ U', then 𝒰 = {U,U'} is an open cover of X where no such connecting sequence (U₁,...,Uₙ) exists. For the other implication, assume that x and y lie in the same component. For an arbitrary 𝒰, define S(𝒰) to be the set of all points z ∈ X such that there is a connecting sequence (U₁,...,Uₙ). Then S(𝒰) is open because if z ∈ S(𝒰) with connecting sequence (U₁,...,Uₙ), then Uₙ is an open neighbourhood of z contained in S(𝒰). It's closed because if w is any point of X such that every neighbourhood V of w intersects S(𝒰) (so in particular if V ∈ 𝒰), say in the point z, then if (U₁,...,Uₙ) is a connecting sequence for z, (U₁,...,Uₙ,V) is a connecting sequence for w. So S(𝒰) is an open and closed set that contains x, so because y lies in the same component as x we get that y ∈ S(𝒰). Because 𝒰 was arbitrary, there is a generalized path from x to y.

So connectedness is equivalent to generalized path-connectedness. You can concatenate generalized paths in the obvious way. It seems you could use such a gadget to define something like the fundamental group of spaces with bad path-connectedness, like the Warsaw circle. But how to define a homotopy relation between generalized paths?

[ralphembree-blog]

Writing Loquitor

At the heart of Loquitor, it runs by signals. When a message is posted, a signal is sent which runs a function. If that function determines that the text in the message is a command, that's another event. The Command signal is sent and also a more specific signal such as Command-test. It's usually the more specific one that has a function attached to it which handles the command. The original ChatExchange library has only one function to handle signals: `Room.watch` in the `rooms` module. Only one function can watch (I think), and it handles every signal. I wasn't satisfied with that little customization, so I wrote the `skeleton` module to create a subclass with more advanced signal-handling. As a GTK+ fan, I imitated their scheme. # **The `skeleton` module** ## How to use When entering a room, you first need to be logged in. This is accomplished with the `chatexchange.Client` class, something like this: from chatexchange import Client client = Client("stackoverflow.com", "myuser@myemailprovider.com", "mYP@sSw0rd") The host that is passed must be one of stackoverflow.com, meta.stackexchange.com, or stackexchange.com. If you don't know which one to use, you should probably use stackexchange.com. That client is then passed to `skeleton.room` along with a room ID like this: from Loquitor.skeleton import Room room = Room(1, client) # 1 is the ID of the Sandbox Once that is done, you can connect to the room's signals. To see which ones are available, you can do this: from Loquitor.skeleton import Events print(Events.events.keys()) You can mostly guess which ones are available by looking at the subclasses of `chatexchange.events.Event` (available by running `pydoc3 chatexchange.events`). You can then connect to those events with something like this: def echo(event, room, client): event.message.reply(event.content) room.connect("message-posted", echo) Note that `event.content` is the HTML-encoded version; you might want to use `html.unescape()` to decode it. That would be a very annoying function to do because your bot would now repeat anything that anybody said. To help with that, I created the main `bot` module. ## How it works The skeleton module adds two new classes: a subclass of `chatexchange.rooms.Room` and an `Events` class. The `Room` class works with the `Events` class to allow connecting to signals more specifically than just a watch for them all. ### The `Events` class The `Events` class is a way of keeping track of which events mean what. It has the `events` dictionary, which maps names to IDs. To add something to it, the `register` classmethod is used. It is given an event name and a class. It then gets an ID from the class by checking the class's `type_id` attribute. Next, it registers the class with `chatexchange.events`. Finally, it makes sure that all `Room` instances have the event registered. This is because each room keeps track of which events go to which functions with a dictionary. If the event wasn't in existence until after the creation of the room, the event's name will not be a key in the dictionary and trying to connect to it would result in an error. ### The `Room` class The `Room` class is just like `chatexchange.rooms.Room` except that it has the `connect`, `disconnect`, and `emit` methods. The `connect` and `disconnect` methods are merely easy ways of modifying a dictionary. The `emit` method is where the action happens. Connecting an event to a function is fairly simple, but I just *had* to make it more complicated. Well, it also happens to be useful. Instead of just a simple `event_id: function` dictionary, a single entry might be as complicated as this: 12: { 0: { 0: (some_function, (1,)), 1: (some_function, ()), }, 20: { 2: (important_function, ()), } } The 12 is the ID of the event. In that ID, there is a dictionary of priorities to functions. For the default priority (0), we have two functions to call. "Why the 0 and 1?" you might ask, "and why is `some_function` there twice?" Each time you use `room.connect()`, a new connection ID is created. The 0 and 1 are IDs. In this way, a single function could be called twice (as is the case here). In our case, the function is called as `some_function(1)` and then is called again as just `some_function()`. "But you could just make a list. Why do you need IDs?" When an ID is used, it can then be reverted later. A second dictionary is being maintained also that keeps track of where these IDs are. For our example, it would look like this: 0: (12,0), 1: (12,0), 2: (12,20), The `disconnect()` method can now take an ID, say 2. It checks the ID dictionary and finds that it is at 12 and then 20. It looks at the events dictionary at the 12 key. It then looks at the 20 key of that dictionary. The result is our dictionary of connection IDs to functions. It can then remove the ID that we are looking at (2), and that function will no longer be called when the 12 event happens. A little more on priorities, in case you missed it. The `some_function` and `important_function` are in separate sections. When the `emit` method is looking through 12's dictionary, it looks at the highest numbers first (higher priority). It therefore looks at 20 before it looks at 0 and calls the functions in this order: `important_function()`, `some_function(1)`, `some_function()`. Now the `emit` method is what actually uses this dictionary. At the end of `Room.__init__`, we use `watch` to send all events to `emit` (with multithreading). Any other uses of `emit` are done manually. The `emit` method is given an event (an instance of a class with a `type_id` attribute) and a logged-in client. It then checks the event ID with the events dictionary. For each priority (in descending order), it calls each function with the following arguments: the event, the room, the client, and then whatever extra arguments were specified in `connect()`. If, at any point, one of the functions returns True, the loop breaks and no other functions are called. This could be helpful, for example, if one wanted to prevent the bot from responding to messages containing containing indecent language. You could connect the `message_posted` event to a function with high priority and then `return True` if it contained indecent language. No further functions would be called, and it would be just as if the message hadn't been posted. # **The `bot` module** ## How to use The `bot` module offers the `Bot` class and the `Command` class. The `Command` class is mostly meant to be subclassed. It is used in `bot.register` (explained below). The `Bot` class is a way of converting message-posted events into Command events. The `Bot` arguments are as follows: * room: a `skeleton.Room` instance * client: a `chatexchange.Client` instance * config_dir: a directory path in which command configuration files will be stored * no_input: a boolean (True or False) that indicates if keyboard input can be accepted Once you have a bot, you can then register commands with the `register` method. It is given a command name, a function, and (optionally) some help text. In addition to registering commands, you can also register replies to bot messages. For example, the `pause` command runs like this: user: >>pause 5 minutes bot : (reply ^) No more messages will be received for 5 minutes. Reply `cancel` to cancel. user: (reply ^) cancel bot : I will now receive messages. To register a reply, you will need the ID of the original message posted by the user (`>>pause 5 minutes`). This is because I don't currently know how to get the ID of the message the bot posted. This can be used something like this: def cancel(event, room, client): event.message.reply("Nah, never mind. You can't cancel.") def pause_command(event, room, client, bot): message_id = event.data['message_id'] bot.register_response(message_id, on_cancel) # Do something about the pause command ## How it works ### Command registration The command registration is handled by the `Bot.register` method. It is given the name of the command, a function to call, and (optionally) the help text. It then creates a new subclass of `bot.Command` with the name `Command-commandname` and registers that class with `skeleton.Events`. Next, it uses `skeleton.Room.connect()` to register the function with the newly-created signal. The `help` attribute of the new class is set, and the command name and class are added to the commands dictionary. ### When a message is posted In the `bot` module, I create a new kind of event. It is called `Command`. If you want to, you can have a function called whenever a command is given. I connect the "message-posted" signal to a method called `on_message`. In there, the message is parsed to see if it is a command. If it is a command, the command is checked against our dictionary of commands. If nothing is found, the user who posted the command is informed that no such command exists. Otherwise, we do a couple things. First, we do some better HTML parsing. This is done with `html.unescape()`. Next, we define the "query" as the text after the name of the command, or "5 minutes". The `query` of `event.data` is set appropriately. We then try to get a list of arguments from the query string. This is done with `csv.reader()`. We define the csv separator as a space, but the `csv` module is still helpful because it listens to the presence of quotation marks. This sly trick was taken from somebody on Stack Overflow. I don't remember his name. Once the event is all setup with attributes, we use `room.emit` to call the function associated with this command. For error handling, that call is put in a `try` block and any exception is sent to the calling user with "Oops. That's an error: " prepended to it. ### When there is a reply In addition to the "message-posted" event, we listen to the "message-reply" event. In `on_reply()`, we find the parent of the parent of the message. This is because the parent of a reply to the bot would be the message of the bot. The parent of that is the original message posted by the user. To get this grandparent, we use `event.message.parent._parent_message_id`. We then check this against our dictionary. If it exists, we do the same query parsing as mentioned above and then call the function registered for this response. If no function is registered, we simply ignore the message.