#fraisse theory

[m---a---x]

Inspired by all the newly created communities i have also created one about the topic closest to my heart: Foundational Mathematics

It is inteded for all types of posts about and from people of all kinds of backgrounds interested in the topic.

Please share with anyone you think might be interested. If you want to be added comment on this post, so I can add you.

[eatsleepmath]

An illustration of the Cherlin-Hrushovski construction

The following construction, due to Cherlin and Hrushovski, provides an example of an \(\aleph_0\)-categorical theory which is not \(G\)-finite, nor which has the small index property: take an infinite set \(A\), and expand it by equivalence relations \(E_n\) on each power \(A^n\) such that each \(E_n\) has two infinite classes and the finite imaginaries \(\{A^n/E_n\}\) are all independent. Call the resulting structure \(\mathfrak{A}\).

\(\operatorname{Aut}(\mathfrak{A})\) then has \(\left(\mathbb{Z}/2 \mathbb{Z} \right)^{\omega}\) as a quotient.

By increasing the number of equivalence classes, one can encode as a quotient of \(\operatorname{Aut}(\mathfrak{A})\) arbitrary countable products of finite symmetric groups. By introducing more predicates, one can cut down on the number of symmetries and thus encode as a quotient of \(\operatorname{Aut}(\mathfrak{A})\) arbitrary countable products of finite groups. By introducing relations which interpret functions between finite sets of imaginaries in \(\mathfrak{A}^{\operatorname{eq}}\), one can encode as a quotient of \(\operatorname{Aut}(\mathfrak{A})\) an arbitrary separable profinite group. For more detail, see Evans and Hewitt’s 1990 paper Counterexamples to a conjecture on relative categoricity.

The purpose of this post is to explicitly write down (indeed, even draw, with many colors!) what the structure \(\mathfrak{A}\) encoding \(\left(\mathbb{Z}/2 \mathbb{Z} \right)^{\omega}\) as a quotient of \(\operatorname{Aut}(\mathfrak{A})\) looks like. The existence of \(\mathfrak{A}\) is usually justified by taking a Fraïssé limit of an appropriate class of structures, which to me always seems rather black-boxy. So, I went to the trouble of writing down what \(\mathfrak{A}\) might look like. As it turns out, our calculation of \(\mathfrak{A}\) will show, rather nicely, why one should expect such an \(\mathfrak{A}\) to pop out of a Fraïssé construction in the first place.

In an appropriate category \(\mathbf{Struct}\) of multisorted first-order structures and interpretations, we can achieve \((\mathbb{Z}/2\mathbb{Z})^{\omega}\) as a quotient of some \(\operatorname{Aut}(\mathfrak{A})\) with much less work. In an abandoned chapter of my master’s thesis, I showed that given a projective diagram of groups \(G_i\) with projective limit \(G\), one can take the invariant/canonical structures of the actions \[\operatorname{Inv}\left(G_i \curvearrowright G_i\right)\] and form their colimit \(\mathfrak{B}\) in \(\mathbf{Struct}\), which has a sort for each \(G_i \curvearrowright G_i\), with definable functions linking the sorts corresponding to the transition maps in the original projective diagram. The automorphism group of \(\mathfrak{B}\) is \(G\), and it is easy to find a multisorted structure \(\mathfrak{A}\) which interprets \(\mathfrak{B}\) such that the induced continuous map \(\operatorname{Aut}(\mathfrak{A}) \to \operatorname{Aut}(\mathfrak{B})\) is surjective.

Of course, putting the equivalence relations on disjoint sorts completely bypasses the interesting part of the problem of writing down the Cherlin-Hrushovski construction in a \(1\)-sorted structure \(\mathfrak{A}\): we have to arrange the equivalence relations on \(A\), \(A^2\), \(A^3, \dots\) to be independent despite interference from the diagonal and projection maps linking the powers of \(A\).

Here’s an example that shows that this is not a vacuous problem. Given an equivalence relation \(E\) on \(A\), there is an induced equivalence relation \(E'\) on \(A \times A\), given by the kernel of the natural map \[A \times A \twoheadrightarrow A/E \times A/E, \text{ by } (a_1, a_2) \mapsto (a_1/E, a_2/E).\]

(Incidentally, this shows that a product of imaginary sorts is an imaginary sort in \(T^{\operatorname{eq}}\).)

Then it is impossible to find an automorphism of \(A\) which fixes the \(A/E\) while permuting \(A^2/E'\): if \(a\) and \(b\) are not \(E\)-equivalent, then \((a,b)\) and \((b,a)\) are not \(E'\)-equivalent, and any automorphism which interchanges the \(E\)-classes of \(a\) and \(b\) will interchange the \(E'\)-classes of \((a,b)\) and \((b,a)\).

So let’s proceed with the illustration. Let’s just try to encode \(\mathbb{Z}/2\mathbb{Z} \times \mathbb{Z}/2\mathbb{Z}\) on \(A\) and \(A \times A\) first. Getting just \(\mathbb{Z}/2\mathbb{Z}\) is easy, since any equivalence relation with two infinite classes on \(A\) will do. So, our task is to figure out how to specify \(E_2\) on \(A \times A\). The identity map always gives us the identity group element \((0,0)\), so now we just have to achieve the generators \((0,1)\) and \((1,0)\).

We’ll let the underlying set \(A\) be an interval, say \([-1,1]\), and we’ll specify \(E_1\) on \(A\) by coloring \(A\) half green and half-purple:

and so \(A/E_1\) consists of green and purple:

Now we have to figure out how to color \(A \times A\) blue and orange:

Let’s go to a toy example and temporarily replace \(A\) with the finite set \(A = \{a,b,c,d\}\), such that \(E_1 \rightrightarrows A\) is given by coloring \(a,b\) green and \(c,d\) purple. Here’s \(A \times A\):

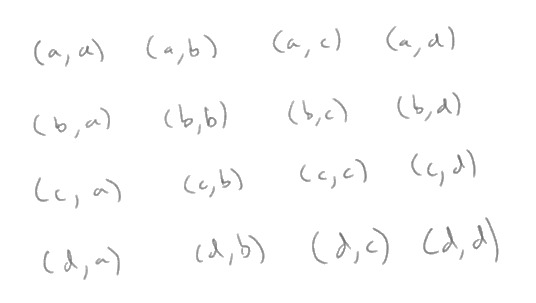
Since the identity permutation fixes everything, an immediate candidate for an automorphism of \(A\) which fixes green and purple but which interchanges blue and orange (whatever we specify that to be) is the permutation which interchanges \(a\) with \(b\) and \(c\) with \(d\). Here’s what it does on pairs:

Similarly, assuming the previous guess is consistent, if we want to interchange green and purple but fix blue and orange, an immediate candidate is given by interchanging \(a\) with \(c\) and \(b\) with \(d\). Here is its action:

Now, by just eyeballing this we can work out a coloring. Suppose that \((d,a)\) was orange. Then since the red arrows are supposed to permute \(E_2\)-classes, \((c,b)\) must be blue. Since the blue arrows are supposed to fix \(E_2\)-classes, \((b,c)\) must be orange and \((a,d)\) must be blue. Continuing in this way, we arrive at the following coloring of \(A \times A\):

Now let’s go back to \(A = [-1,1]\). There’s an obvious way of tranposing the previous coloring to \(A \times A = [-1,1] \times [-1,1]\), by cutting up \(A \times A\) into \(16\) pieces:

Mutatis mutandis, everything works: the following automorphism induces \((0,1)\):

While this automorphism induces \((1,0)\):

Now it’s clear what to do to extend this to an encoding of \((\mathbb{Z}/2\mathbb{Z})^n\) for any \(n\), e.g. to get \(n = 3\), color \(A^3\) as follows:

and so on, as long as the subdivisions are all happening along a single axis.

Going back to the finite model \(A = \{a,b,c,d\}\), we see that we don’t have the resolution to see \((0,0,1)\) in the \(n = 3\) case, so we have to use \(2^3\) elements instead. But then the same reasoning that we used for \(n = 2\) works.

The fact that we reasoned with automorphisms of finite models (\(A = \{a,b,c,d\}\)) and then extended the automorphisms to an infinite model (\(A = [-1, 1]\)) is an instance of the ultrahomogeneity property of a Fraïssé limit. Indeed, the Fraïssé construction proceeds by taking all possible finite models that we could perform our previous argument with and smashing them together. Another consequence of the general Fraïssé-theoretic machinery is that the resulting \(\mathfrak{A}\) is existentially closed. This rules out the possibility of obstructions like \(E_2 = E’\) as we noted above.

[mergist]

I tried reading a book called Logic Without Borders, which seemed to be an attempt to show interconnections between mathematical meta-models or philosophies like model theory, category theory, ZF set theory, the intuitionist continuum, etc. Unfortunately I've been kicked out a bit by the language.

Math writing fascinates me, but there are so many things that looking-up can't penetrate because they're the surface-level extensions of towers of thought. It feels like poetry to read about "the Ehrenfeucht-Fraisse game of length w between non-isomorphic countable models U and B". Like, wow, I hope they're having fun.

[tranzitcz]

Presentation and discussion about the book The Right to Truth. Conversations on Art and Feminism

PRESENTATION AND DISCUSSION

about the publication The Right to Truth. Conversations on Art and Feminism, ed. Oksana Briukhovetska, Lesia Kulchynska

Tuesday September 17 at 6:30 pm, tranzit.cz, Dittrichova 13, Praha 2

The publication will be presented by Oksana Briukhovetska, artist, co-author and designer of the book. Afterwards, a discussion with our resident, Anna Kravtes, and curators Tereza Stejskalová and Zuzana Štefková will take place.

The publication The Right to Truth. Conversations on Art and Feminism represents the collection of 20 interviews with female artists, curators, activists and thinkers of different generations from 7 countries (Ukraine, Russia, Belarus, Poland, Czech Republic, France, US). This selection embodies a history of meetings and conversations, which emerged from the search for answers to question about the role of art in the process of the transformation with the aim to achieve emancipation and freedom for all discriminated groups. In this context, art is presented together with activism and the activities of institutions and curators who work in them to recreate the atmosphere of mutual influence that exists in real life. The publication, therefore, presents the first hand knowledge on the current feminist art practices and activism.

Interviews: Valentyna Petrova, Dana Kavelina, Oksana Briukhovetska, Alina Kopytsa, “Feminist Workshop”, “FemSolution”, Irina Solomatina, “Gender Route”, Victoria Lomasko, Alma Lily Rayner, Zuzana Štefková, Artwall Gallery, Feminist (Art) Institution, Zuzanna Janin, Aleka Polis, Sylwia Nikko Biernacka, “The Machine of Changes”, Rébecca Chaillon, ORLAN, Geneviève Fraisse, Morgane Lory, “HF”, Isabelle Alfonsi, Marcelle Alix Gallery, Flora Katz, Martha Rosler.

The book is in two languages – Ukrainian and English.

Oksana Briukhovetska

Artist and curator based in Kyiv, member of the VCRC. Her curatorial projects include, among others, the feminist exhibitions Motherhood (2015), What in Me is Feminine? (2015) and TEXTUS. Embroidery, Textile, Feminism (2017). In 2018 she was co-curator and participant of the Neighbors Warsaw under Construction X Festival . She writes artistic texts and articles about art. She works with themes such as physicality, social exclusion, and the status and role of women. She has participated in exhibitions in Ukraine and abroad.

Lesia Kulchynska

Curator, lecturer, researcher, publicist, PhD in Film Studies. She works at Visual Culture Research Center (Kyiv) since 2011. Among the curated projects: Ukrainian Body (2012), Unrendered Spaces (2011-2014), discussion platform Between Revolution and War (2014), exhibition and research project Some Say You Can Find Happiness There (2015), The School of the Lonesome program of The School of Kyiv – Kyiv Biennial 2015, performance and exhibition project The Raft CrimeA (2016). She researches in image theory and film theory fields.

[bspolink1348]

Nouvelles lectures en BSPO (13/05/19)

À la une : Le revenu de base inconditionnel : une proposition radicale / Philippe Van Parijs, Yannick Vanderborght

Cote de rangement : HC 79 .I5 V 257411 / Domaine : Économie

« L’idée de revenu de base inconditionnel est désormais au cœur des débats sur l’avenir de nos modèles sociaux. Elle consiste à verser à chacun un revenu régulier à titre individuel, sans contrôle des ressources ni exigence de contrepartie. Diffusée en France à l’occasion de l’élection présidentielle de 2017, elle avait été peu auparavant soumise à référendum en Suisse et a fait l’objet de plusieurs expérimentations à travers le monde.

Rédigé par deux spécialistes internationalement reconnus, ce livre offre la première synthèse systématique de la discussion aujourd’hui mondiale sur cette proposition radicale. Il explore ses origines historiques, discute les objections éthiques, économiques et politiques qu’elle soulève et jauge sa pertinence face aux défis écologiques et à la mondialisation. Il fournit un recueil d’informations fiables et d’arguments éclairants qui doivent être utiles à ceux qui plaident pour le revenu de base, mais aussi contre lui, en aidant à corriger les nombreuses erreurs factuelles et confusions conceptuelles que l’on trouve de part et d’autre.

L’ouvrage n’en constitue pas moins un plaidoyer engagé en faveur d’une idée qui vise à rendre notre société plus libre et notre économie plus saine. Il ne manquera pas d’enthousiasmer, ou du moins d’intriguer, toutes celles et tous ceux qui veulent que le monde de demain soit plus juste et comprennent que, pour cela, notre modèle de protection sociale doit être profondément réformé.

Philippe Van Parijs est responsable de la chaire Hoover d’éthique économique et sociale à l’Université catholique de Louvain et professeur invité à l’Université de Harvard. Co-fondateur du BIEN en 1986, il en préside aujourd’hui le Conseil international.

Yannick Vanderborght est chargé de recherches au Fonds national belge de la recherche scientifique (FNRS) et enseigne la protection sociale comparée à l’Université catholique de Louvain. Il est membre du Comité exécutif du Basic Income Earth Network (BIEN) »" - Quatrième de couverture

Sciences politiques

Aujourd'hui la guerre : penser la guerre : Clausewitz, Mao, Schmitt, adm. Bush / Catherine Hass

Cote de rangement : B 105 H 257414

A people betrayed : the role of the West in Rwanda's genocide / Linda Melvern

Cote de rangement : DT 450 .435 M 257426

Congo / Thomas Turner

Cote de rangement : DT 658 .26 T 257422

Comment gouverner un peuple-roi ? Traité nouveau d'art politique / Pierre-Henri Tavoillot

Cote de rangement : JA 83 T 257406

Géopolitique : méthodes et concepts / Barbara Loyer

Cote de rangement : JC 319 L 257405

Empires of the mind : the colonial past and the politics of the present / Robert Gildea

Cote de rangement : JC 359 G 257424

Économie

Irving Fisher / Robert W. Dimand

Cote de rangement : HB 119 .F5 D 257423

The political economy of inequality / Frank Stilwell

Cote de rangement : HC 79 .I5 S 257416

Travail

Améliorer les appariements sur le marché du travail / Alexandra Roulet

Cote de rangement : HD 5708 .67 R 257413

Anthropologie

Anthropologie et philosophie du sensible / Roger Somé

Cote de rangement : BD 450 S 257410

Sociologie

Tiny publics : a theory of group action and culture / Gary Alan Fine

Cote de rangement : HM 716 F 257421

Tyranny of the moment : fast and slow time in the information age / Thomas Hylland Eriksen

Cote de rangement : HM 851 E 257420

Nationalizing sex : fertility, fear, and power / Richard Togman

Cote de rangement : HQ 766 T 257425

Gender and political theory : feminist reckonings / Mary Hawkesworth

Cote de rangement : HQ 1075 H 257418

La fabrique du féminisme / Geneviève Fraisse

Cote de rangement : HQ 1613 F 257412

Communication

Shooting a revolution : visual media and warfare in Syria / Donatella Della Ratta

Cote de rangement : P 94 .65 D 257419

Friending the past : the sense of history in the digital age / Alan Liu

Cote de rangement : PN 4560 .3 L 257417

The truth matters : a citizen's guide to separating facts from lies and stopping fake news in its tracks / Bruce Bartlett

Cote de rangement : PN 4784 .F27 B 257415

Arts

Design & crime / Hal Foster

Cote de rangement : NA 2543 F 257408

Histoire de la colonne infâme / Alessandro Manzoni

Cote de rangement : PQ 4713 M 257409

Mobilité

Les voitures autonomes : comment les voitures sans chauffeur transforment nos modes de déplacements et créent une nouvelle industrie / Hod Lipson et Melba Kurman

Cote de rangement : TL 152 .8 L 257407

Tous ces ouvrages sont exposés sur le présentoir des nouveautés de la BSPO. Ceux-ci pourront être empruntés à domicile à partir du 27 mai 2019.