#danseiji iv

[map-projection-showdown]

DANSEIJI IV vs SPILHAUS-ADAMS

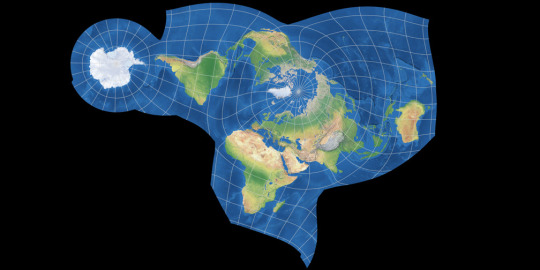
Danseiji IV Miscellaneous Compromise

Created by Justin Kunimune in 2019. Instead of simple equations, the Danseiji projections use a different construction method where a mesh is imagined on a sphere, and then optimised to some constraints by changing the elastic properties and letting it settle. For the Danseiji IV, the aim was to reduce distortion everywhere and introduce a bunch of interruptions in the ocean to handle it, this gives a layout similar to the Dymaxion or the Peirce Quincuncial and could be used in the same ways as them.

Spilhaus-Adams Polyhedral Conformal

Created by Athelstan F Spilhaus in 1979 as an oblique aspect of the Adams World in a Square II, while the Spilhaus-Adams projection looks weird at a first glance, it has a very specific aim: to show all the oceans without interruptions. This goal means that it doesn't care about area distortions on land (resulting in massive distortions in South America and East Asia).

NOTE: because of its unique goals it is usually presented with most of the land round the edge removed, and a couple of repetitions to preserve the gulf of Mexico fully, I would recommend checking below the cut for this before voting.

[link to all polls]

Spilhaus-Adams with excess land removed:

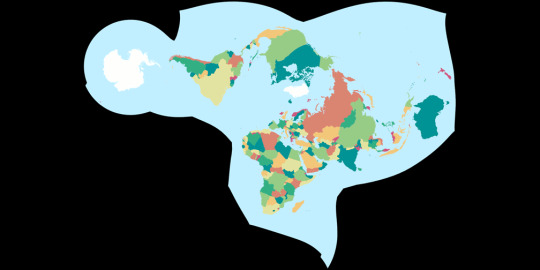
Political:

Tissot's Indicatrices:

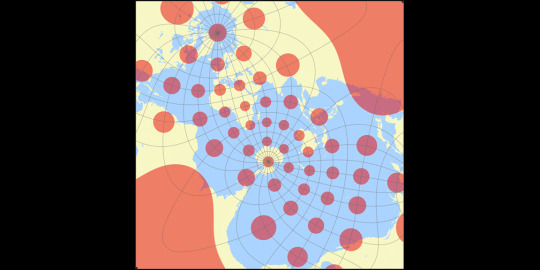
Images created by Tobias Jung (CC BY-SA 4.0) from map-projections.net

[map-projection-showdown]

BONUS POLL: CONTIGUOUS CONTINENT CLASH

I thought I'd do some polls of projections with similar purposes, so I'm starting with a poll comparing projections that aim to show the entire world without interrupting any land.

From left-to-right then top-to-bottom we have the CALM, Lee-Concialdi, Grieger Triptychial, Canters W23, Danseiji IV, and Dymaxion projections. Three conformal projections followed by three compromise projections

The CALM (Conformal Authagraph-Like Map) and the Lee-Concialdi projections on the first row, are both rearrangements of the Lee Tetrahedral projection with different centres to move the distortion to different places depending on which you prefer, I really like the half-hexagon layout of the Lee-Concialdi. The CALM is designed to have the same layout as the Authagraph projection, which I can't include here as they haven't published the equations so no one actually knows how to make it. Both of these are conformal.

The Grieger Triptychial is a rearrangement of the Peirce Quincuncial. It and the next two have very similar layouts, with the Grieger being conformal and the Canters and Danseiji being compromise projections. The other differences between these are mainly in where the distortions are, for example the Galapagos are massive on the Grieger but Antarctica has a weird shape on the Canters.

Last we have the Dymaxion, probably the most famous of these, based off the net of an icosahedron it has a pretty complex layout but a good balance of distortions for a compromise projection.

[map-projection-showdown]

STEREOGRAPHIC vs SPILHAUS-ADAMS

Stereographic Azimuthal Conformal Round 1: [Stereographic vs Eckert IV] Round 2: [Stereographic vs Azimuthal Equidistant]

Spilhaus-Adams Polyhedral Conformal Round 1: [Spilhaus-Adams vs Danseiji IV] Round 2: [Spilhaus-Adams vs Lee-Concialdi]

Two projections that show how not-conformal a conformal projection can look when area inflation gets involved.

The Stereographic is the oldest projection in the tournament, initially used for star charts long before it came to be used for Earth, it represents each hemisphere conformally in a circle, though the area distortion that grows towards the edge does make Brazil and West Africa look weird.

The Spilhaus-Adams is one of the more unique maps in the tournament, presenting a view of earth the prioritises keeping oceans intact rather than landmasses (And in fact beating two other projections with that aim in previous rounds). Given that it distorts land (especially Argentina and China) to unrecognisability, it is usually shown without the land, see below the cut.

[Direct comparison on map-projections.net]

[link to all polls]

[map-projection-showdown]

LEE-CONCIALDI vs SPILHAUS-ADAMS

Lee-Concialdi Polyhedral Conformal Round 1: [Lee-Concialdi vs Guyou]

Spilhaus-Adams Polyhedral Conformal Round 1: [Spilhaus-Adams vs Danseiji IV]

Two projections with double-barrelled names, to denote their authors modification of another projection to meet a specific aim, compete in this final poll of round 2.

Concialdi's modification of Lee's world-in-a-tetrahedron projection is a rearrangement to achieve the goal of presenting all continents including Antarctica without interrupting them, while Spilhaus' modification of Adam's world-in-a-square projection is an oblique aspect to achieve the goal of presenting all oceans without interrupting them (and is usually shown without the land, see below the cut).

Which of these is a more noble goal? Which of them achieves their goal the best? You decide.

[Direct comparison on map-projections.net]

[link to all polls]

[map-projection-showdown]

And we're finished with round one!

There were some very close battles there; the ocean focused Spilhaus-Adams narrowly beat out the low error Danseiji IV, and the general-purpose Robinson almost managed to make a comeback against the Equidistant Conic.

I'll post the polls for the next round tomorrow.

[youzicha]

This is the hardest choice so far I think, both of these are great.

On the one hand, I think the Danseiji IV is maybe the most aesthetically pleasing among the "center at the north pole and try not to distort the shapes too much" maps in the competition. Compared to Dymaxion, Waterhouse Butterfly and Pierce Quincuncial it keeps the continents together better, so you get a good feel for sea routes as well as land routes. If I was designing a board game about U.S.-USSR nuclear war, I might pick this one for the board.

On the other hand, the sea-only Spilhaus-Adams really is iconic. There is a bunch of other "continents centered at the north pole" ones in the running, but only one map for fish...

DANSEIJI IV vs SPILHAUS-ADAMS

Danseiji IV Miscellaneous Compromise

Created by Justin Kunimune in 2019. Instead of simple equations, the Danseiji projections use a different construction method where a mesh is imagined on a sphere, and then optimised to some constraints by changing the elastic properties and letting it settle. For the Danseiji IV, the aim was to reduce distortion everywhere and introduce a bunch of interruptions in the ocean to handle it, this gives a layout similar to the Dymaxion or the Peirce Quincuncial and could be used in the same ways as them.

Spilhaus-Adams Polyhedral Conformal

Created by Athelstan F Spilhaus in 1979 as an oblique aspect of the Adams World in a Square II, while the Spilhaus-Adams projection looks weird at a first glance, it has a very specific aim: to show all the oceans without interruptions. This goal means that it doesn't care about area distortions on land (resulting in massive distortions in South America and East Asia).

NOTE: because of its unique goals it is usually presented with most of the land round the edge removed, and a couple of repetitions to preserve the gulf of Mexico fully, I would recommend checking below the cut for this before voting.

[link to all polls]

Spilhaus-Adams with excess land removed:

Political:

Tissot's Indicatrices:

Images created by Tobias Jung (CC BY-SA 4.0) from map-projections.net