#also. apologies for the barebones image descriptions. idk how to transcribe the math properly and i don't really have the spoons to try
Explore tagged Tumblr posts
Text
Unnonexistence's Notecard Method for Learning Mathematics
Hello! This is the study method I developed after flunking out of first-year university algebra and having to retake it! It may or may not be particularly innovative and it may or may not help you, but I did (eventually) graduate with a Bachelor's degree in math despite having unmedicated ADHD, so, y'know, there's that. I owe it mostly to the notecards.
DISCLAIMER that any example cards are my actual real notes & I am not fact-checking them. They lean towards intuitive rather than strictly correct & were only ever intended to be for personal reference. I did pass these courses, and I think most of the cards are pretty good, but like... use at your own risk.

You Will Need:
A pack of index cards. I like the 3" x 5" ones that are lined on the front and blank on the back.
Some pens you like. I use fine-tip markers in about 4 colours, plus a white gel pen for fixing mistakes. Pencil can get smudgy over time, so it's not ideal.
Any course materials you have (notes, textbook, etc.)
Optionally, a nice box for your index cards. (You can also just use a rubber band or something. Whatever).
General Approach
We're making reference cards. One concept per card. You probably have an intuitive sense of how big A Concept is for you - it should be an amount of information that can comfortably fit in your brain at one time. If it doesn't fit on one or maaaybe two cards, it's probably too big.



Here's a topic I broke up into two cards - Chain Rule and Extension of Chain Rule. One IS an extension of the other, but the information is a lot easier to remember in two chunks. (3 pictures, here, because the first card is double-sided).
You are NOT trying to cram as much information as you can onto each card. You are trying to create an easy reference for yourself, which means making the cards as clear and legible as you can. When it's 5 minutes before your calculus exam and you're having a panic attack because you forgot how the chain rule works, you want to be able to flip through, find that Chain Rule card, and be able to absorb the information on there.
For math courses, A Concept is often a definition, a theorem, a formula, or a problem-solving approach. As much as possible, you want to write it down in a way that makes sense to you. Add any helpful tips or intuitive explanations or things you keep forgetting. If your cards are blank on the back, that's a great place to draw diagrams.

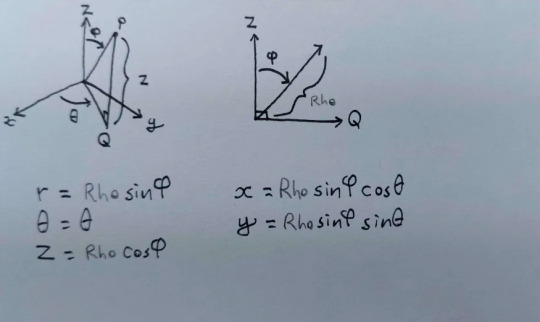
(On the back of this card you can see where I wrote "Rho" in pencil and never bothered to replace it with the symbol, lol. My prof had bad handwriting & I wasn't sure how it was supposed to look.)
Proofs are often too long to fit on a card, but if you have a theorem where the proof is important, it's a good idea to write out a little summary of how the proof works/how to do it.

Ideally, you do the work of Understanding The Concept when you're making the card, and then you can just refer back to it in future. I forget definitions a lot, and this saved me so much time that I would have spent reading one confusing page of the textbook over and over or trying to find stuff in my notes.
I try to keep my formatting mostly consistent. Clear title. Card numbers in the top right corner so I know if anything's missing. Definitions in black ink with important words underlined in colour. I tend to use coloured ink for things like examples and personal commentary. I also use it to create a visual distinction when I do need to cram something on there (not ideal, but sometimes necessary).


The Method
Sit down with your class notes or your textbook. Your goal is to get all the important concepts you're supposed to have learned in this course so far onto notecards. (Probably not all in one go.)
The ideal time to do this is right after each lecture (most math lectures are around 2-5 cards worth of material), but that's easier said than done. I always had a hard time keeping up & all my card decks, as a result, get spottier towards the end of the term. It's fine. Do your best.
I mostly went through the course material in order. I kept checklists of which lectures I had already made cards for, and which ones still needed doing.
If you don't really get something, but you know you need a card for it, at least put the definition down. You can make a better version or add more notes later. I sometimes make placeholder cards with just a title so I'll remember to come back to something.
If you write down a definition, and you're like "this refers to another thing, and idk what it is but it's come up a few times now," you probably need to make a notecard for that other thing.
How I Use The Cards
When you're doing assignments, it's really useful to have your stack of cards there to refer to. If something comes up that you don't remember the definition for, you can look it up. If you're doing proofs, having all the theorems from the course handy is a great way of getting ideas for where to start. If you're doing calculations, it's helpful to have the techniques you need written out step by step.


I spent a lot of my exam prep time making cards and going through the ones I'd made. It gave me a sense of what I already knew and what I needed to spend more time on. Having things broken up into small chunks also made it a lot easier for my brain to hang onto them.
After making cards like this for a few terms, I also found them really helpful for reviewing concepts from previous courses. Sometimes you just need to refresh your memory on something from the prereq so you're not totally lost. I've graduated now & I still refer back to my cards sometimes.
Conclusion
Well, that's my (somewhat rambly) explanation of my main study method! I hope it's helpful for at least a few people out there. I wish you the best of luck learning math & whatever else you might be studying. You've got this!!
#studyblr#mathblr#long post#idk the study tags. whatever#this is me writing without trying to hide the adhd much. hi#it's verbose. words fall out of brain and there are a lot of them. you know how it goes#also tumblr kept EATING MY DRAFT EDITS fuck u tumblr#r.i.p the slightly better version of this post that DIED#mine#numbers do not lie#also. apologies for the barebones image descriptions. idk how to transcribe the math properly and i don't really have the spoons to try#i did try to put the info that's relevant to this guide. theyre just examples of cards so the specific math isnt really important#math
6 notes
·
View notes