#acheni

[pier-carlo-universe]

I fichi: fiori invertiti, non frutti, e il curioso legame con le vespe. Recensione di Alessandria today

Scopri il mondo affascinante dei fichi, tra botanica, biologia e tradizione agricola.

Scopri il mondo affascinante dei fichi, tra botanica, biologia e tradizione agricola. I fichi: una storia che capovolge le nostre certezze Spesso considerati un frutto, i fichi sono in realtà qualcosa di molto più complesso e affascinante. Dal punto di vista botanico, il fico non è un frutto singolo, bensì un’infruttescenza, ovvero un insieme di piccoli frutti chiamati acheni, racchiusi in una…

[weaseltotheface]

The fun part of belly achenis that not only is it like a nausea thing but I still am also like cramping a lot from period off an on so im just like in suffer town rn

I rly did think i was gonna feel better 😔 stupid breakfast. Stupid cramps.

[lucemaria]

Perché la fragola per un rituale d’amore? 🍓 ❤️ ⤵️

Perché la fragola per un rituale d’amore? ❤️🍓

La sua forma a cuore prefigura l’amore, tanto da aver avuto la forza anche di mutare un mito: Ovidio infatti racconta che quando Adone muore tra le braccia di Venere, dopo essere stato ferito da un cinghiale scagliato contro di lui dalla gelosia di Marte, il suo sangue, venuto a contatto con il terreno, si trasforma in un rosso fiore. 🍓

Tuttavia la forma a cuore della fragola e gli acheni che la punteggiano, così simili a piccole gocce, hanno creato la leggenda che vede nascere tanti piccoli cuori rossi, le fragole appunto, dall’unione delle lacrime di Venere con il sangue dell’amato Adone. ❤️🏛❤️

Anche nella mitologia nordica la fragola è associata all’amore, essendo l’attributo di Frigg, dea del matrimonio. 💒

E la forma e il colore ne fanno ancora oggi l’emblema dell’amore e dell’eros tanto da attribuirgli anche effetti afrodisiaci, seppure non sia così.

#ritualedamore #fragole #significato #amore #fioredelparadiso #magia #magiarossa #luce

[rwizakakiza]

Somo: TABIA 25 ZA KUEPUKA NA HATARISHI KWENYE MAISHA YAKO. (Part 3: KUT...

Somo: TABIA 25 ZA KUEPUKA NA HATARISHI KWENYE MAISHA YAKO.

---------------------------------------------------

SUBSCRIBE (Tumaini Jipya Duniani Tv)

Https://youtube.com/@rwizakakiza?si=ewqb8Z8S1aeDwoRB

Sehemu: III

----------------------

3. 1. TABIA YA 1: "KUTOKUSAMEHE". (Tunaendelea na....)

MATOKEO /DALILI ZA MTU MWENYE TABIA YA KUTOKUSAMEHE.

(e). KISASI

Hii ni dalili au matokeo ya kutokusamehe ambayo inafanya mtu kujenga chuki kwa yule aliyemkosea na kuapa kumlipiza kisasi. Kisasi ni nia thabiti ya ndani ya kulipiza ubaya uliotendewa na hauko tayari kusamehe.

Kutokusamehe kunamjengea mtu kuamini kwamba kisasi ni njia ya kutatua maumivu aliyonayo kutokana na alichotendewa, kumbe hajui anaongeza hasira na chuki zinazoweza kuleta kifo na madhara mengine mengi.

Mtu aliyejaa Msamaha, kisasi chake ni kuzidisha mema kwa anayemkosea. Yaani analipa mema kwa mabaya aliyotendewa.

.....Wapenzi, MSIJILIPIZE KISASI, bali ipisheni ghadhabu ya MUNGU; maana imeandikwa, Kisasi ni juu yangu mimi; mimi nitalipa, anena BWANA. Lakini, Adui yako akiwa na njaa, mlishe; akiwa na kiu, mnyweshe; maana ufanyapo hivyo, utampalia makaa ya moto kichwani pake. Usishindwe na ubaya, bali uushinde ubaya kwa wema.

....Rum 12:19-21.....

BWANA YESU akaagiza hivi

......Mmesikia kwamba imenenwa, Jicho kwa jicho, na jino kwa jino, Lakini mimi nawaambia, MSISHINDANE na mtu mwovu; lakini mtu akupigaye shavu la kuume, mgeuzie na la pili. WAPENDENI ADUI zenu, WAOMBEENI wanaowaudhi,

......Mathayo 5:38-44.....

(f). UHASAMA

Kutokusamehe kunasababisha mafarakano, chuki na kutoelewana baina yako mwenyewe usiyesamehe na aliyekukosea. Na haishii hapo mpaka kwenye kizazi chenu kinapandikizwa kuchukiana na hamwezi kusaidiana kwa sababu ya uhasama uliopo kati yenu

Na matokeo yake ni Ukatili, Dhuluma Jeuri na mauaji vinajenga makazi ndani yako, moyo wa huruma unatoweka.

....Tamaa mbaya zimo ndani yake; Dhuluma na hila haziondoki mitaani mwake.

...... Zaburi 55:11.....

(g). UGOMVI

Matokeo mengi ya ugomvi, baina ya mtu na mtu, kwenye familia au jamii, nchi na nchi ni KUTOKUSAMEHE. Wengine udhani kushinda kwa nguvu ya kimabavu amemaliza vita kumbe anatengeneza Migogoro na vita ambayo haitaisha.

.....Mtu wa hasira huchochea ugomvi; Bali asiye mwepesi wa hasira hutuliza mashindano.

......Mithali 15:18....

.... Mwanzo wa ugomvi ni kama kutoboa penye maji; Basi acheni ugomvi kabla haujafurika.

.....Mithali 17:14.....

Ugomvi unauacha kwa kusamehe kwanza wewe na kusameheana inakuja baadae, Wewe kwanza samehe ili ulete amani.

Tabia ya KUTOKUSAMEHE inakuwa tabia ya kudumu usipotii Neno la MUNGU (kuamua kusamehe) na ina madhara mengi kama tulivyoona na mengine mengi. Yakupata utambue tabia ya kutokusamehe ni tabia hatari sana kwenye maisha yako (kuanzia kwenye afya yako, maisha yako ya kiroho na Kizuizi kikubwa cha Sala zako kutojibiwa na wewe mwenyewe kutokusamehewa na MUNGU, Epuka tabia hii kwa kusamehe.

.......Basi MSIPOWASAMEHE watu makosa yao, wala BABA yenu (MUNGU) HATAWASAMEHE ninyi makosa yenu.

.....Mathayo 6:15.....

3. 2. TABIA YA 2: "HOFU".

.........Tutaendelea.........

Rejea

"But if YOU DO NOT FORGIVE others [nurturing your hurt and anger with the result that it interferes with your relationship with GOD], then your FATHER will NOT FORGIVE your trespasses".

..... Mathew 6:15....

Kwa msaada zaidi:

Ev. Erasmus Pascrates Kakiza

+255 782 546 914

+255 764 215 291

Rwizakakiza@gmail.com

@2024 The year of my shining.

[vjhero]

Cartoon - Acheni Jokes (official video)

[susannastigler]

Mi piace in quegli angoli illuminati dalla luce della mattina comporre le raccolte di semi, piante e cortecce che ho raccolto di recente. Sembrano ali leggere, al contrario del loro nome un pò duro, “Achenio”. E’ allora che un ritaglio di cigni svolazzanti si unisce alla danza. Mi allontano e li lascio muoversi assieme *Video installazione > Link in bio* . . . #seasonal #acheni #swan #dance #setdesign #details #light #collect #treebark #nature #ispiration #photography #stilllifephotography #creative (presso Florence, Italy) https://www.instagram.com/p/CKWKa6mlPvr/?igshid=1q2mx9i0lg2dq

[francescointoppa]

Frutti (acheni e pappi) di Boccione maggiore

[mteulethebest]

Waziri wa Fedha na Mipango, Dr.Philip Mpango akiwa Hospitalini Dodoma leo

Waziri wa Fedha na Mipango akiwa Hospitalini Dodoma leo

“Shukrani ya kwanza ni kwa Mungu, amenitendea makubwa, kutoka nilikokuwa siku 14 za Madaktari kunihudumia nyumbani mpaka wakanihamishia hapa, acheni Mungu aitwe Mungu, tuendelee kumtukuza, yeye ndio muweza wa yote, amenipa nafasi ya kuendelea kuitumikia Nchi yetu” “Nimekaa hapa Hospitali ya Benjamini Mkapa Dodoma nikihudumiwa, hapa peke yake leo ni siku ya 14, nilikuja na mtungi kabisa wa…

[eda11y]

infructescences of Platanus orientalis.... by gerbonis

[mamo7478]

cortili

In questo cortile assolato tra i panni stesi ad asciugare crescono i soffioni e tra risa di bimbi volano aquiloni più lontano di quanto pensi. Soffio gli acheni al vento e i miei sogni verso i tuoi sensi.

Marco Corradi

[tobeeclectic]

Watch "Bien x Aaron Rimbui - Mbwe Mbwe (Official Music Video)" on YouTube

Acheni MBWE MBWE.....

Washa ki2 shetwain ahepe......🌬️

[tanzaniampyanews]

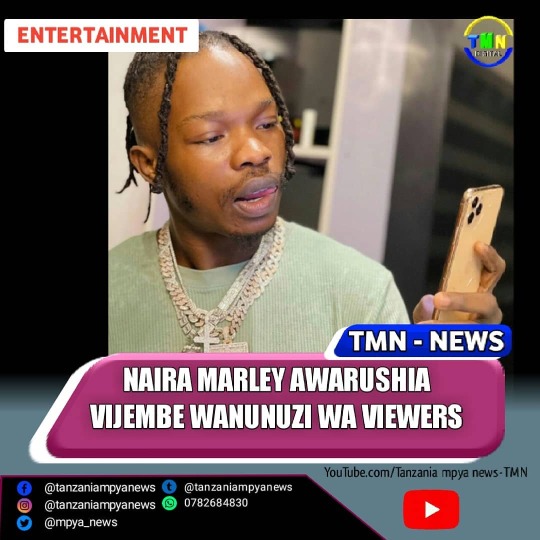
MWANAMUZIKI WA NIGERIA NAIRA MARLEY | AWARUSHIA VIJEMBE WASANII WA AFRIKA MASHARIKI AWATAKA WAACHE KUNUNUA VIEWERS YOUTUBE;- Mkali wa Ngoma ya "COMING" inayofanya poa sana Katika Chart za Muziki Nchini Nigeria Hasa katika Mitandao ya Apple music , Spotify na ITune Chart, Naira Marley amewarushia vijembe wanamuziki wa Afrika Mashariki hasa akiwalenga Watanzania ambao wamekuwa na kasumba ya kununua 💰 viewers ,na Trending number #1 katika Mitandao wa YouTube hii kadhia kwa wasanii ambao wana hadhi Underground ndio wamekuwa wakifanya ili waonekane kuwa wapo juu Lakini ukiangalia Takwimu za mitandao mingine zipo chini. 🔻 Naira Marley kupitia Instagram Story yake Ameandika kuwa 'Acheni kununua Viewers YouTube kwani Like zitatuonyesha Mimi hata nikizungumza juu ya msanii yeyote kutoka Nigeria Nina uhakika hakuna Msanii wa Nigeria aliyewahi kununua Viewers na haitawahi kutokea kwa wasanii wa Nigeria 🔺 Alimalizia Naira Marley. hivi majuzi tulipost Tanzania mpya news kulikemea swala hili swala linaharibu taswira nzima ya Muziki wetu hii itasababisha wanamuziki wa Tanzania kuonekana ni Local na hawana sifa za kuwa International Artist na hii inaweza ikasababisha kukosa Nominated katika Tuzo kusema ule ukweli Mwanamuziki ambae ana hadhi ya uanamuziki wa International ni Alikiba maana katika muziki wake hatumii mbinu chafu kama zinazotumiwa na wengine anategemea Mashabiki zake kuupambania muziki wake Tanzania mpya news tukiwa kama wadau wa Burudani hatujasema kwa ubaya ila tumesema kwa maslahi mapana ya industry yetu ya muziki. https://www.instagram.com/p/CQ-YsU6L5FT/?utm_medium=tumblr

[soudybrown]

Yanga Kaeni Kwa Kutulia, Acheni tufturu Kwanza, Leo Mnachezea Vidude Vya Kutosha Kutoka Kwa Mnyama wa Msimbazi, Simba 🦁 Fungulia @cloudsfmtz Mchezo Ipo Live kutokea Mkapa Stadium “Dar Derby” https://www.instagram.com/p/COnWaTlscT8/?igshid=1b3dqx7r2wcai

[newscheckz]

Memo No. 21 From the National Welfare Desk of Men

New Post has been published on https://newscheckz.com/memo-no-21-from-the-national-welfare-desk-of-men/

Memo No. 21 From the National Welfare Desk of Men

Losing is Part of Life: How Not to Lose Like Donald Trump

JOIN NEWSCHECKZ TELEGRAM FOR MORE INSIGHTS AND PERSONAL EXPERIENCE: https://t.me/Newscheckz

Several months ago, we were enjoying a drink in a bar, when an old friend, the worst arseh*le I have ever had to deal with joined us.

He stayed with us briefly, ordered a round drinks for the five of us. Once the round was done, he ordered for some expensive whiskey. Then he made an Irish exit.

We only realized when it was time to pay, and there was a pending bill of Sh 13, 700, that he was supposed to have picked.

The bill now was upon us and we had to rob Mshwari, raid Fuliza, invade the Talas of these world until the bill was settled.

We were so mad, if met him moments afterwards, we would have attacked like we were a pack of wolves.

We were so angry at that SOB, and when we called him the following day, this is what he had to say, “Pombe si ni nyinyi mlikunywa? Nyinyi mkiniona, naeza buyia mandume mzinga? Acheni ufala?”

He hang up. He had even forgotten the first round of beers he had ordered for us. I was mad at myself, because I had cut off the bastard like five years earlier when he had proved he will never grow up to be a man.

But there is one trait that has always intrigued me about him: His total lack of shame. His inability to think how his actions can hurt others.

He not only has a careless tongue, but he is also prone to fights, never repays a debt, and can still call to borrow money from you.

It is a trait I have seen in some men, who think, everything in life should go their way.

And no man exemplifies this more than the outgoing American president, Donald J Trump.

Donald Trump has achieved a lot in life. Born with a silver spoon in the mouth, his father was a Real Estate magnet, whose canvas was no greater a city, than New York.

From the late 1970s and early 1980s, Trump took charge of his father’s property business, became a New York playboy, in between built some grotesque monuments across America, ventured into Casino business, failed horribly, gamed the system with taxation and bankruptcy games, entered the big stage of Reality TV, before stumbling into politics as a hobby and ending up as the most powerful man in the world.

By and large, this is a life that 99 percent of the people in the world can only fantasize. Money, lots of it, fame, all of it, women, most of them. Everything.

Here is the irony of life, Trump was not going to win a re-election. If he won, it would have gone against the very script of life.

History always elevates losers to the top, but their time at the top is never a smooth one, and often they crash out, and end up disgraced.

Gaddafi, Mugabe, Mobutu, and what may happen to Museveni. But the sad thing about life, even if Trump won a second term, or even became the president of the entire world, he will never be satisfied.

And that is why, he has not conceded and has only grudgingly allowed the transition authority to ‘cooperate’ with incoming administration.

Trump had a chance to concede much earlier, however grudgingly and walk away with a modicum of dignity and he could always look back at the records he shattered, save for the Covid-19, which he bungled (it is hard to tell, how democrats would have fared in all fairness), but the world will always remember him as an egregious loser who went against that most, exemplary and decent of traditions: peaceful transfer of power in the world’s No. 1 democracy.

I have seen many men like Trump who never admit to a loss, can never accept defeat and have a totally distorted view of themselves and the world.

I see men, who think, because of their power and position, their women can’t leave them, or cheat on them and when confronted with the reality, they either die of depression or go on rampage.

I see men who can’t accept an election loss, who can’t see that their business is collapsing, their marriage is ending.

Their ego cannot allow them to come to terms that sometimes life humbles you. Men who can’t seek help when undergoing a problem.

Men who keep on faking it, hoping they will make it, even when there is overwhelming evidence that they are doomed to fail.

It depends on their upbringing. Some people were raised as spoilt brats, their parent (s) and siblings never saw the need to nip their bad behaviour it the bud.

We all know adults who are a pain in the arse. Adults who love themselves too much, they can make love to their image in the mirror.

You know users. Guys who are so shameless, they can fish a phone, and call you after four and half years and proceed straight away to ask for a favour.

Guys who are arrogant for no reason, who believe so much in their ability, they think they are infallible.

I have news for them. It is OK to be humble. It is necessary to be selfish. But at the very least how the world works.

1. The world can exist without you.

2. Nobody really gives a damn about you. There may be some hangers-on and bootlickers, but these ones abandon you as soon as they smell your bankruptcy.

3. How you treat people always comes back to reward or to haunt you. I know very many lonely folks in their 30s and 40s, but they are lonely because they were self-centered young men, who thought everything will always work their way.

Now life has humbled them and can’t believe that the world still rotates and revolves.

The worst thing that can happen to this lot is to lose. Whether an argument, a good deal, a good woman, anything.

Often they totally lose their head, and cannot internalize what hit them.

Yet, if you are a man, losing is part of life. We lose all the damn the time. But as the cliché says, whatever you lose, don’t lose the lesson.

So, if you are a man, and currently losing out on something, undergoing some kind of rejection, remember, Man’s rejection is God’s protection.

When you lose, be gracious, be grateful, and mourn like a human being, but don’t mourn too long.

Pick up the pieces, dust up and know the job ahead is always the most difficult.

For arrogant folks, with no self-sense of awareness, understand losing is part of life. And if you have a friend who is self-centered, you owe them a rebuke, a reprimand, every time they act like arseholes.

Each human being must learn how and when to be proud, but more importantly, when to be humble.

Don’t be like Donald Trump and embarrass yourself, in your own small world. Cut your losses when you have to, let her go however bad your ego can’t allow it, admit you are/were wrong, and above all, learn.

In life, we win some, lose some. Champions are those who know how to bounce back.

[michele72]

Fichi Secchi

Area di produzione Intero territorio regionale. Caratteristiche del prodotto Le piante hanno un notevole sviluppo, prediligono clima caldo e terreno sciolto. I frutti, a forma di pera, hanno colore diverso a seconda le varietà (verde, bian- co, nero); contengono numerosissimi acheni avvolti in una polpa zuccherina, dolcissima. Metodiche di lavorazione I frutti raccolti a maturazione completa, sani, privi di…