#Tor Thom

[clarounette]

NEW AUDIO: MORE THAN I COULD by Adriana Locke

NOW LIVE!!! The audiobook of More than I could by Adriana Locke, narrated by Maxine Mitchell and Tor Thom, is available!!! Blurb This grumpy single dad falls hard for the nanny. Chase Marshall is many things: An attentive single dad. Jaw-droppingly gorgeous. My employer for the next 30 days. He’s also the bane of my existence. He swears I’m a never-ending headache—the most infuriating…

[gronglegrowth]

Throckmorton "isn't a wizard but is extremely convinced they are" vs Thom "is a wizard but wishes they weren't"

[positively-knotted]

Thom Isomorphism & the Euler Class

As promised, another longpost. This one might be a bit more technical than others I've done recently, but hopefully still approachable to someone who's done a reasonable course in algebraic topology (Ch 1-3 of Hatcher) and also knows what a fibre/vector bundle is. The end goal will be to introduce the Euler class as a generalisation of the Euler characteristic, and to motivate characteristic classes more generally.

A Brief Note on Vector Bundles

It's always difficult to know where to start with these things, but let's assume that you know what a vector bundle is, and that I don't have to motivate working with them. In case you've only seen them for manifolds before, observe that the definition works just as well for any reasonably nice space - I'll assume everything is a CW complex, although CW approximation means I don't actually have to.

A more interesting idea is this. To any manifold M, we have a canonical vector bundle TM, the tangent bundle. So if something is a property of manifolds, we can ask whether it is actually a property of TM, and if so, can it be generalised to other vector bundles? Suprisingly the answer is often yes.

The Leray-Hirsch Theorem

I can't prove everything, so let's state a theorem that we'll use later. Ignore the theorem numbering, and cohomology is taken with R-coefficients.

You should think of this as a version of the Kunneth theorem, that generalises from products to more general fibre bundles. Condition (i) is just a rephrasing of the vanishing of the Tor term - like the in the Kunneth theorem, it's automatic if we take R to be a field. (ii) is a niceness condition on the bundle, and it's a good exercise to check that it will be satisfied for a product.

I actually lied slightly, we're going to use a relative version of this. But like always in algtop, if you can believe the absolute version, you can believe the relative version.

The Thom Space

Suppose we have a rank n vector bundle π: E -> B. This is a bit annoying algebraically, because E homotopy retracts onto B no matter how twisted it is. So to capture any non-triviality we need to be a little bit clever. First, observe that we get a disc bundle π: D(E) -> B by just choosing a closed disc in fibre. (If we're in a manifold, choose a metric and take the unit disc. If we're not, you have to work a little harder to show this is well-defined). Now D(E) is a manifold with boundary, which is a sphere bundle S(E) -> B. Take the quotient D(E)/S(E) by collapsing the whole boundary to a point. We call this the Thom space T(E) of the vector bundle. Notice that T(E) is uniquely determined by π, but is definitely non-trivial!

As an example, take B= S^1, and consider the two line bundles. If E is the orientable line bundle, T(E) looks like a sphere with two points identified, so is homotopy equivalent to S^1 v S^2 [exercise]. If E is the non-orientable line bundle, then T(E) is RP^2.

You might notice that this is no longer a fibre bundle over B, as the point S(E)/S(E) lives in every "fibre". Oh well. It does have a nice CW decomposition though! First , give T(E) a single 0-cell, the point S(E)/S(E). Then suppose B has a fine enough decomposition that π is trivial over each cell [this is actually automatic, bc discs are contractible]. Each i-cell in B lifts to a (i+n)-disc in D(E), and under the quotient this is an (i+n)-cell in T(E). Like in my last post, you have to do a little bit of work to check that this really is a CW decomposition, but hopefully you believe me. You should double check with the line bundles over a circle that these do in fact give the usual cell structures.

Now, let's make the reasonable assumption that B is connected with a single 0-cell, so T(E) has one 0-cell, one n-cell, and no cells of dimension 1,...,n-1. Let's also suppose that π is R-oriented; that is, either the vector bundle is oriented and R is any ring, or it is unoriented and R = Z/2. Then the coboundary map of the n-cell to he (n+1)-cells is trivial [exercise: think about the boundary map from the 1-cells to the 0-cell in B]. In particular, H^n(B) = R, and has a canonical generator coming from the choice of orientation! We call this the Thom class of E.

The Thom Isomorphism

More often, we work in relative cohomology, using the fact that

H^*(T(E)) = H^*(D(E), S(E)) = H^*(E,E\B).

Here the first isomorphism is the usual relative <--> quotient; the second is excision, and I'm identifying B with the 0-section. This is nice for the following reason. Given a choice of orientation, on each fibre F of E, we have a canonical generator of H^n(F, F\0). [This is possibly your definition of orientation, but if not then it's equivalent]. The Thom class is a class in H^n(E,E\B) that restricts to the generator on the fibre over the 0-cell. But the 0-cell was chosen arbitrarily, so in fact it restricts to the generator on every fibre! It's not obvious that such a class exists, so it's nice to see that it does.

Finally, let's apply the (relative) Leray-Hirsch theorem. H^i(F,F\0) is free for all i since F is just a vector space; condition (ii) is met by the Thom class! We can then make two final simplifications. Firstly, H^*(B) is isomorphic to H^*(E) by pulling back under π. Secondly, H^i(F,F\0) is either 0 or R, so vanishes in the tensor product. Putting it all together, we get the following.

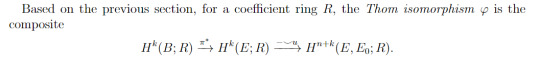
Phew! That's a lot of work, and we haven't even gotten to the Euler class yet.

The Euler Class

This is surprisingly easy. Remember that the Thom class lives in relative cohomology H^n(E,E\B). We can always pull back a relative class under inclusion to an absolute class u' ∈ H^n(E). Identifying this with H^n(B) again by π, we get the Euler class e(π) ∈ H^n(B)

Sometimes it's more helpful to think of it as follows. By the abstract nonsense that is the relative cup product, u⌣u = u'⌣u. So we get the following equivalent definition:

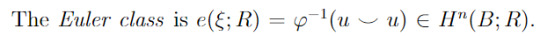
This can be nicer to work with, as u⌣u is a square so has some nice properties. For example, take the following basic facts:

(a) is true by checking that the Thom class pulls back - this follows directly from viewing it as the unique class restricting to the generator on fibres.

(b) is true by the same observation.

(c) is quite hard to prove using the first definition that we gave, but it follows directly from the fact that u⌣u = -u⌣u if n is odd. Note that this is a weaker version of the statement that the Euler characteristic of an odd dimensional manifold is 0!

(d) These are both actually kinda tricky, but it's not hard to convince yourself it's true.

Ok this post is already way too long, so I'll delay the main point until next time, when I'll link the Euler class to Poincare duality, and eventually to the actual Euler characteristic. For now, a teaser of why else it might be useful:

The first bullet follows directly from (c)+(d) above. For the second, suppose we had a nowhere-zero section s: B -> E\B. Writing i for the inclusion E\B -> E, we get the composite πis = id_B. But π^*e(π) = u' by definition, and i^* u' = 0 since u' is the pullback of a relative class! So e(π) = s^*(0) = 0.

As a sanity check for where we're going, recall that S^1 and S^3 have nowhere-zero vector fields while S^2 doesn't. The Euler characteristic of S^1 and S^3 is zero, while the Euler characteristic of S^2 is 2. This is looking promising!

[444namesplus]

Aal Aam Aan Aar Aas Ala Ale Ali Alo Alu Ama Ame Ami Amo Amu Ana Ane Ani Ano Anu Ara Are Ari Aro Aru Asa Ase Asi Aso Asu Baa Bal Bam Ban Bar Bas Bee Bel Bem Ben Ber Bes Bii Bil Bim Bin Bir Bis Bol Bom Bon Boo Bor Bos Bul Bum Bun Bur Bus Buu Chaa Chal Cham Chan Char Chas Chee Chel Chem Chen Cher Ches Chii Chil Chim Chin Chir Chis Chol Chom Chon Choo Chor Chos Chul Chum Chun Chur Chus Chuu Daa Dal Dam Dan Dar Das Dee Del Dem Den Der Des Dii Dil Dim Din Dir Dis Dol Dom Don Doo Dor Dos Dul Dum Dun Dur Dus Duu Eel Eem Een Eer Ees Ela Ele Eli Elo Elu Ema Eme Emi Emo Emu Ena Ene Eni Eno Enu Era Ere Eri Ero Eru Esa Ese Esi Eso Esu Faa Fal Fam Fan Far Fas Fee Fel Fem Fen Fer Fes Fii Fil Fim Fin Fir Fis Fol Fom Fon Foo For Fos Ful Fum Fun Fur Fus Fuu Gaa Gal Gam Gan Gar Gas Gee Gel Gem Gen Ger Ges Gii Gil Gim Gin Gir Gis Gol Gom Gon Goo Gor Gos Gul Gum Gun Gur Gus Guu Iil Iim Iin Iir Iis Ila Ile Ili Ilo Ilu Ima Ime Imi Imo Imu Ina Ine Ini Ino Inu Ira Ire Iri Iro Iru Isa Ise Isi Iso Isu Kaa Kal Kam Kan Kar Kas Kee Kel Kem Ken Ker Kes Kii Kil Kim Kin Kir Kis Kol Kom Kon Koo Kor Kos Kul Kum Kun Kur Kus Kuu Ola Ole Oli Olo Olu Oma Ome Omi Omo Omu Ona One Oni Ono Onu Ool Oom Oon Oor Oos Ora Ore Ori Oro Oru Osa Ose Osi Oso Osu Paa Pal Pam Pan Par Pas Pee Pel Pem Pen Per Pes Pii Pil Pim Pin Pir Pis Pol Pom Pon Poo Por Pos Pul Pum Pun Pur Pus Puu Saa Sal Sam San Sar Sas See Sel Sem Sen Ser Ses Shaa Shal Sham Shan Shar Shas Shee Shel Shem Shen Sher Shes Shii Shil Shim Shin Shir Shis Shol Shom Shon Shoo Shor Shos Shul Shum Shun Shur Shus Shuu Sii Sil Sim Sin Sir Sis Sol Som Son Soo Sor Sos Sul Sum Sun Sur Sus Suu Taa Tal Tam Tan Tar Tas Tee Tel Tem Ten Ter Tes Thaa Thal Tham Than Thar Thas Thee Thel Them Then Ther Thes Thii Thil Thim Thin Thir This Thol Thom Thon Thoo Thor Thos Thul Thum Thun Thur Thus Thuu Tii Til Tim Tin Tir Tis Tol Tom Ton Too Tor Tos Tul Tum Tun Tur Tus Tuu Ula Ule Uli Ulo Ulu Uma Ume Umi Umo Umu Una Une Uni Uno Unu Ura Ure Uri Uro Uru Usa Use Usi Uso Usu Uul Uum Uun Uur Uus Vaa Val Vam Van Var Vas Vee Vel Vem Ven Ver Ves Vii Vil Vim Vin Vir Vis Vol Vom Von Voo Vor Vos Vul Vum Vun Vur Vus Vuu

[innerdreamercollective]

Wedding the Wide Receiver by @authorlisasuzanne is now LIVE in audio! 

Narrated by: Tor Thom and Kelsey Navarro Foster

Listen today!

Audible: https://geni.us/WTWRaudible

Amazon: https://geni.us/WTWRaudio

Apple: https://bit.ly/3B4pJTb

Goodreads: https://bit.ly/4e86ebb

#SportsRomance #AccidentalMarriage #Athlete #FakeMarriage #MarriageofConvenience #valentineprlm @valentine_pr_

[anitabyars]

New Release from Sawyer Bennett

Foster (Pittsburgh Titans, Book #13)

Synopsis:

When Foster McInnis’ ex-wife flakes and he finds himself with full custody of his daughter, the nanny he hires brings a new complication—an attraction he can’t ignore, no matter how hard he tries.

I love being on the ice and am grateful for my hockey career, but the off season is my favorite time of the year because it brings me my one true love—my daughter, Bowie Jane. Between my job and my ex-wife living across the country, the time I get to spend face-to-face with my kiddo is limited, though we make up for it with summers full of fun adventures. We’re thick as thieves and take full advantage of our time together, but the distance away from her is killing me.

My fortunes change when my ex walks away and I find myself with full custody. But with the hockey season looming, I know I’m going to need help taking care of Bowie Jane. Enter Mary Elizabeth Archer—otherwise known as Mazzy. Highly recommended to me through the Titans’ network, Mazzy crashes into our life like a hurricane. She’s unlike anyone I’ve ever met and to say I’m intrigued is an understatement. But no matter how attractive she is, no matter how I crave to know everything about her, I can’t go there. It’s inappropriate. Just wrong, wrong, wrong, even though she might be the most right thing I’ve ever known.

Being the indescribable force she is, there is soon no corner of our lives that Mazzy hasn’t impacted in a positive way. And my desire for more with her becomes far stronger than my misguided idea that I could ever resist this woman. Our attraction burns hot and keeping our eyes, hands and mouths off one another gets harder by the minute. It doesn’t take long for me to know that I’m all in with Mazzy. She’s my end game and, lucky for me, winning is my specialty.

Grab your copy of Foster directly from Sawyer by shopping the Sawyer Bennett Bookstore!

✦ E-Book and Audio (audio narrated by Tor Thom and Maxine Mitchell): https://bit.ly/STORE_Foster

✦ Signed paperback (available to US mailing addresses): https://bit.ly/Foster_PB

You can also get Foster at the following retailers:

✦ Amazon: https://bit.ly/49T7DAa

✦ Nook: https://bit.ly/48W0kGr

✦ Apple: https://apple.co/3TmfYVI

✦ Google: https://bit.ly/4agAPB0

✦ Kobo: https://bit.ly/49OonZc

Not sure if you're ready to commit to Foster? Sawyer's got you covered!

✦ READ the first three chapters: https://bit.ly/Foster_Chapters

✦ HEAR the first chapter: https://bit.ly/Foster_Audio

About the Author:

New York Times, USA Today, and Wall Street Journal Bestselling author Sawyer Bennett uses real life experience to create relatable stories that appeal to a wide array of readers. From contemporary romance, fantasy romance, and both women’s and general fiction, Sawyer writes something for just about everyone.

A former trial lawyer from North Carolina, when she is not bringing fiction to life, Sawyer is a chauffeur, stylist, chef, maid, and personal assistant to her very adorable daughter, as well as full-time servant to her wonderfully naughty dogs.

If you’d like to receive a notification when Sawyer releases a new book, sign up for her newsletter (sawyerbennett.com/signup).

Connect with Sawyer:

✦ Facebook: http://bit.ly/Sawyer_FB

✦ Reader group: http://bit.ly/Sawyer_NEP

✦ TikTok: https://bit.ly/Sawyer_TOK

✦ Instagram: http://bit.ly/Sawyer_IG

✦ Goodreads: http://bit.ly/Sawyer_GR

✦ BookBub: https://bit.ly/Sawyer_BB

✦ Newsletter: http://sawyerbennett.com/signup

[cocktailsfairytales]

🏒❄️ NOW IN AUDIOBOOK ❄️🏒

𝐎𝐧 𝐭𝐡𝐞 𝐋𝐢𝐧𝐞 by Julia Connors is LIVE in AUDIO!

Narrated by the amazing CJ Bloom & Tor Thom

Listen to the audiobook! https://amzn.to/3JAYRv3

Besides swoon-worthy moments, you can also expect:

💙He falls first…and HARD

💙Second chance

💙Enemies to friends…to lovers

💙He hates everyone but her

1-CLICK TODAY: https://geni.us/ontheline

Blurb:

My marriage wasn't perfect, but my husband's unexpected death yanked away my sense of security and left me floundering.

Enter Jameson Flynn, former NHL star and my late husband's sports agent, who's back in my life as the executor of the will. Things between us are as contentious as when we worked together five years ago, except now we're working together to navigate all of the secrets and deceptions my husband left behind.

I remember Jameson as arrogant, condescending, and heartless. And yet, he repeatedly shows up for me and my daughters—helping me pick up the broken pieces and put my life back together.

Now, I'm seeing a side of him he only reveals to people he truly cares about. He's protective in a way I didn't know I'd like, caring in a way I didn't know he was capable of, and still sexy as hell.

The problem is he broke my heart a long time ago. But the closer I get to Jameson, the more I see that the only thing easier than hating him might actually be loving him.

[joyffree]

🎧 We are so excited to share that Survive (Houston Defiance MC Series) by K E Osborn is available NOW in 𝗔𝘂𝗱𝗶𝗼𝗯𝗼𝗼𝗸!

🎧↓ 𝐒𝐭𝐚𝐫𝐭 𝐋𝐢𝐬𝐭𝐞𝐧𝐢𝐧𝐠 𝐓𝐨𝐝𝐚𝐲 ↓🎧 Audible: https://adbl.co/3TcCQqI Apple: https://apple.co/48T2EOlGoogle Play: https://bit.ly/3VtkMM3B&N: https://bit.ly/3IsZsOXKobo: https://bit.ly/3vefx7XAudiobooks: https://bit.ly/3T88w0E 🎧 Narrated by Tatiana Sokolov & Tor Thom

We started a war. One we thought we could win. The moment the club tried to outsmart the Militia, the battle lines had been drawn. As the brotherhood of the Houston Defiance MC, our job is to be loyal. To show respect when it's due. There are ranks in place for a reason. Prospects will fight the system. Those we love will fall. Chaos will rule the streets of Houston. Can the club survive, thrive, evolve? Change is on the horizon. The dawn of a new age. Romances will flourish, the enduring relationships will prosper. But not everything is smooth sailing. Everyone will be tested. But in the end, will Houston Defiance Survive?

🎧 Also Available in Audio 🎧 ➜ https://adbl.co/3DwdjRP

Hosted by Enticing Journey Book Promotions

[libertyreads]

Book Review #13 of 2024--

Such a Lovely Family by Aggie Blum Thompson. Rating: 4 stars.

Read from February 22nd to 24th.

Before I get into the review, a quick thank you to NetGalley and the publishers over at Tor for allowing me access to this ARC in exchange for an honest review. Such a Lovely Family follows the Calhouns on the night of their annual Cherry Blossom Party. The D.C. elite love to show up to the family's gorgeous house and view the cherry blossoms in full bloom. But what no one expected was for the night to end in murder. Now a police investigation is underway and this picture perfect family's dark secrets start to come out. When their money can no longer get rid of the Calhouns' problems and they find themselves backed into a corner, what will they do to make sure they come out on top? Such a Lovely Family comes out on March 12th and is available for preorder now.

I was surprised when I finished this book and found myself wanting to give it a 4 star rating. I usually don't give Adult Mystery novels that high of a rating. Usually there's a problem with pacing or something in the ending that ruins it for me. But, surprisingly, not this time. I love some rich people drama because it's so absolutely absurd. It was giving the Grayson family from Revenge which I ate up. We follow the Calhoun family on the day of the party as little secrets start to come out and all of the drama gets laid out. Why did the flowers never arrive? Why is Ellie Grace so focused on getting the perfect photos? Why won't Nate open up about his ex-wife? What is going on with Trey's sobriety? And why is Thom's grin just a little too forced? I loved this small community setting of the uber rich with all of its little daily dramas happening in the midst of the murder investigation. I also found the characters to be well rounded. My favorite character was Nate's fiancée who is meeting the family for the first time and sucked into its vortex. I enjoyed the outsider's perspective. And I just have to say that the last couple of pages of the book were practically perfect for me. Specifically the final sentence. It leaves a sense of foreboding that punctuates the story so well. It also leans into the conversation that could be had about communities like this, neighborhoods like this.

The main problem I had with this one was how obvious some of these little secrets are while you're reading the book. Some of them were completely out of left field for me and were pretty good. But some of them I called pretty early on. The overarching mystery of who committed the murder and why and how was a pretty good surprise. I will also say that the ending is a little sloppy. It was sloppy in a way that can make sense, but made me feel like the author had to pull a few things together at the end to make it all work.

Overall, I had a surprisingly good time with this one. It had a lot of the things I was really looking for in an Adult Mystery. I was originally planning on taking five days to read this one so the fact that I read it in three really speaks to its readability.

[tastywordgasms]

A sizzling, grumpy-sunshine, boy-obsessed, one-night-stand romance from USA Today best-selling author @marnimann... The Playboy by @marnimann is now LIVE! #MarniMann #EroticRomance #ContemporaryRomance #AlphaHero #BadBoyGoodGirl #Billionaire #OneNightStand #Playboy #bookclub #bookish #booklover #booksta #bookstagram #bookworm #readersofig #readersofinstagram #valentineprlm @valentine_pr_

Download today or read for FREE with #kindleunlimited  https://geni.us/leXbc Audio Narrated by: Savannah Peachwood & Tor Thom Goodreads: https://bit.ly/3OybFED The Playboy by Marni Mann is now live!  A sizzling, grumpy-sunshine, boy-obsessed, one-night-stand romance from USA Today best-selling author Marni Mann ��� Spade. People know what to expect when they hear my last name. Billionaire.…

[kellysbookblog]

Hendrix: A Pittsburgh Titans Novel Sawyer Bennett Release Date: June 6, 2023

My Amazon: https://www.amazon.com/gp/customer-reviews/R3TUYMTW0I06NI?ref=pf_ov_at_pdctrvw_srp

My GR Review: https://www.goodreads.com/review/show/5591031475

Synopsis:

Hendrix Bateman is one of The Lucky Three, a trio of players who were not on the Titan’s team plane the night it crashed. Feeling as if he’s been given a second chance, Hendrix is determined to make the most out of his life, but that doesn’t mean he’s not suffering from scars that can’t be seen.

 When I lost my Titan brothers in the crash, it was a mixed bag of emotions. I was devastated and grief stricken, but I was also grateful to be alive. Yeah, that might cause a little—okay, a lot of—guilt, but now I’m determined to live each day as if it’s my last.

 A night out with friends puts me in the crosshairs of Stevie Kisner—the devastatingly beautiful bar owner with a sharp tongue and a fire in her eyes that lets me know she has zero tolerance for guys like me. I’ve never been one to back away from a challenge, so I’m not dissuaded by Stevie’s tough as nails attitude or her big biker dad who looks like he wants to kill me. Fueled by too many shots and the raucous urging of my teammates, I set out to show Stevie I’ve got game both on and off the ice.

 While I shouldn’t be looking for anything more than a good time, I can’t help but be captivated by Stevie. She’s cool as hell and we burn hot together. But the more I get to know her, the more I can tell she’s holding something in reserve, and let’s just say I’ve got some trust issues after my last disastrous attempt at a relationship. Now I need to decide if I’m going to let my past dictate my future or if I am willing to put my heart on the line to find out if Stevie is exactly what I think she is—my everything.

 Get Hendrix: A Pittsburgh Titans Novel in digital, signed paperback and audio (narrated by Tor Thom and CJ Bloom) direct from Sawyer: https://bit.ly/HendrixPO

 Download Hendrix: A Pittsburgh Titans Novel at the following retailers:

➜ Amazon: https://amzn.to/3P6s9BU ➜ Nook: https://bit.ly/3Q7fqAl   ➜ Apple: https://apple.co/3BRfrnX   ➜ Google: https://bit.ly/3P4OKig ➜ Kobo: https://bit.ly/3d85x6U  

 PLEASE NOTE: Ebooks purchased from the Sawyer Bennett Bookstore will be delivered via BookFunnel and can be sent to the e-reader of your choice. Audio will be available exclusively on the Sawyer Bennett Bookstore for approximately 90 days before releasing at all retailers and libraries (excluding Audible). Hendrix is narrated by Tor Thom and CJ Bloom. Audio purchase from the Sawyer Bennett Bookstore must be enjoyed within the BookFunnel app (which is VERY user friendly and FREE!).

   About the Author:

 New York Times, USA Today, and Wall Street Journal Bestselling author Sawyer Bennett uses real life experience to create relatable stories that appeal to a wide array of readers. From contemporary romance, fantasy romance, and both women’s and general fiction, Sawyer writes something for just about everyone.

 A former trial lawyer from North Carolina, when she is not bringing fiction to life, Sawyer is a chauffeur, stylist, chef, maid, and personal assistant to her very adorable daughter, as well as full-time servant to her wonderfully naughty dogs.

 If you’d like to receive a notification when Sawyer releases a new book, sign up for her newsletter (sawyerbennett.com/signup).

  Connect with Sawyer:

✦ Facebook: http://bit.ly/Sawyer_FB   ✦ Reader group: http://bit.ly/Sawyer_NEP  

✦ TikTok: https://bit.ly/Sawyer_TOK       ✦ Instagram: http://bit.ly/Sawyer_IG

✦ Goodreads: http://bit.ly/Sawyer_GR   ✦ Newsletter: http://sawyerbennett.com/signup

[skylightbooks]

CATALOG PICKS BY CHARLES!

MONOGRAPH

SLOW WRITING

AUTONOMOUS

QUANTUM PHYSICS FOR BABIES

[444namesplus]

Ahb-pser Ahg Ahm-spaàn Ahn-ord Ald-deh Ald-nar Alf Alf-ors Alk-fa Alk-thián Alm-saàh Aln Alp Als-tsiàr Alt-shan Ard-urb Arf-alt Arf-stan Arg Arg-kran Arg-stem Arn Arp-oàld Aàrg-irk Aàrk-shan Aàrn-psun Aáhb

Bah Bah-kil Bah-spuám Bal Bar Be Ber Bir-shol Biàh-irp Biá Bo Bor-skos Boàr-fil Boáh-kià Bram Brim-fe Brin-aáhn Bris Brol Brum Bu Char Char-ksin Chas Chel Chem-dar Ches Cheàl-sil Chil Chil-guàl Chim-tel Chir Chon Chor Choàl-par Choàn Chul-bren Chul-iàlg Da Dal-bol Dal-ort Dar-ge De Deh Deh-far Di-ahp Dir-thin Dià-spel Do-irn Do-toh Dol Doá-dril Dran Draàr Dreàm-chel Drum-uárm Du Du-frar Ehb-irf Ehd Ehg-psir Ehm-da Ehm-ilp Ehn Ehp-sper Elb-ohs Elf-ki Elg Elg-tson Elk-ksan Elk-uhm Elm Els-faà Els-orp Erb Erd Erf Erf-tsoàn Erk-tur Erm Ern Ern-meh Erp Ers Ert-chus Ert-uhb Eàhd-aàrg Eàhf Eàhn-ba Eáhf-eln Fa-fe Fa-then Fal-ird Faá Feh Fer-chos Feà-peàr Feá Fil-ksis Fo For-iálg Frar-alb Frel Fren Frim Frin Frir Friàm-mo Frul-oàrs Frur Frur-uàhg Fu Ga-uld Gah-ihd Gal Gaà-frum Gaáh Gaál Ge Ge-foh Geh-ku Gel Gi Gih Gir Già Gor-kiàh Goá-tsas Grel Grer-geh Gril Grin-duh Gron Gruám-ksiàr Gu-skan Gur Ihb Ihd-ma Ihf Ihf-psis Ihg Ihk Ihm Ihn-ulb Ihp-psum Iht Ild-spal Ilk-elp Ilm Ilm-irg Iln Ilp Ilp-kiá Ilt-ald Ilt-spiàl Irb Irm-teáh Irn-shim Irp Irs-ehd Irs-peá Irt-spol Iàrd-pi Iàrt-ma Iáhg-tar Iáhk-ulb Iáhm-aáhf Iáhs-skos Iárf Ka-irg Keh Kel Ker-frel Ki-ard Kol Kol-ilg Koár Krer-toh Kriás Krol-tser Kros-prus Krun Ksal-nul Ksal-uhn Ksam Ksar Ksar-ahk Ksaám Ksem-pu Ksil Ksor Ksul Ksun Ksur-mor Ku-ker Kuh Kuàr Kuàr-thin Kuál Ma-ko Mah Maár-ksus Mel Mer Meà-fral Mi-duàl Mi-shel Mià-skoám Mo Mo-ti Mor Mu-erk Mu-taàr Na-ksuàl Naá Ne Ner-faál Ni Nih-psol Niàl No No-si Noh-so Nor Nu Nu-mal Nu-mi Nur-psoàl Ohb Ohd-psom Ohs-ful Ohs-kuàh Olb-ehs Old-koh Olf-goh Olg Olk-aht Olk-ihf Olm Oln Oln-eht Oln-nal Olt-ald Olt-sir Orb Org-tsul Ork-tu Orm Oàhs-from Oàrm Oàrn-ohk Peh Pel-alk Pil Pir Po-thor Poál-droàl Praál Pril-uld Prum-no Psam Psel-ba Psim Psir Psis Psis-dral Psol-kor Psom-erd Psum Psus Puáh-stus Sa Sa-foh Sal Sar Saàl-tor Se-iárt Se-ter Sel-ksel Sel-pson Seá Shar-orn Sher Sher-ta Shin-tral Shir-iáht Shon-erf Shos Shul-skur Shur-fu Shus Si Sir Skam Skan Skas-saá Skas-stul Skaàs-thom Skem-urn Sken Skeàr Skil-psem Skim Skin-tiál Skir-ehs Skir-erd Skir-gron Skol-pi Skon Skoàs Skum-chol Skun-tu Skur-mu Skus So-deh Soh Sor-elg Spam Spam-pi Span Spaám-uáhf Spem-fiáh Spem-stam Spes-no Spis Spiás-ki Spos Spun Stal-iln Stan Star Stas Staán-ilf Stel-bo Stes-thin Steál-naá Stim-erg Stir Stiàn-naáh Stom Stor-elf Stor-iàhk Stos Stos-spes Stum Stum-shel Stun Stuás Su Su-thir Suh Suá-thur Ta-ohk Tar-als Taá Than-skom Thel Thel-da Then Ther-noh Theàn-ahg Thil-po Thin Thin-erg Thir-ma Thir-stuás Thol-psuám Thon-uhd Ti Tih Tià To-stas Trel Trem-ksuám Tres-doà Tril-erm Tril-ilp Trun Tsal Tsam Tsar Tsel-ner Tsel-skil Tsin Tsis Tsom-bor Tson-su Tsor-irt Tsor-spil Tsoám Tsuàm-psaàs Tu Tuh Tul Tuàr Uhb Uhd Uhd-iàrd Uhg Uhk Uhm Uhs Uht Ulg Ulp Uls-alb Uls-chin Urb Urg-stel Urg-sul Urk Urm Urs Uáhp Uáhs Uálb-ksam Uálp

Ahgbeuhk Ahkputhem Ahmkeleàhd Ahnoáhm Ahtksel Algsahsa Alguhn Almnoàhse Altmaál Arbgel Arbssasgul Arfdris Arkksorthil Arndanul Arsark Arskornil Arsssim Artthisshus Aàldpsun Aàrkelfork Aáhgther

Baahsthun Banor Baorb Bareáhk Barksor Baáfahdran Befi Bekoh Bemehars Berahkilp Beshos Bethumahg Biluàrnulk Bofiard Bolehtilm Bothoánssal Bramssen Brimorbfrus Brinchilbe Briàlelpgril Briàrcheás Brumno Brusardnor Buerbchan Bufrim Buhthir Buihbfal Bulbrararf Bursirthir Chaliáhspsel Charurt Chaàsthimehk Cheschinohs Cheàndaà Cheànpsin Chiloáhd Chimksarshos Chinardtoà Chinehm Chingraàs Choreàlgorn Chorksumksol Choàmgemeá Chulelmpi Chumchel Chuámohk Daàhehb Dedurahp Deilm Dielgohm Dilgrer Dirtal Dourd Doápi Draniárm Drarorkfil Drelalk Drenirbfrus Drilsahper Droáldoàuàlp Drulgal Dufagil Duilssoá Dulils Dulnosu Dulnoàhdreàr Durthus Ehboàlnchom Ehfolgirg Ehguhbdah Ehkulg Ehmshul Ehppsoál Ehpthal Elfird Elfshum Elgbresfil Elkpi Elkuhf Elkuàrfird Elpirm Elpirp Elpthoám Eltksos Erbchis Ergbuulp Ermern Ernchas Ernuárb Eàhtchuànmi Eàrbulmihd Eàrkgipsan Eàrkuárgpir Eárnohfpuh Faleln Faàrahb Faáurt Fehnuorm Fodessal Folchertrum Fooárt Fortul Fronbroárelt Fronfruám Frorchas Fruriàhpoálk Fuhberduár Fuhihg Fulgromtruál Fuliáhs Furchonna Gahilf Garthiám Gaàkià Gaàpo Gelurfold Geàlchil Giksumpi Girso Gitoà Giàmu Gogilsaá Goáltros Granirt Grensororf Grenssusuhp Greántih Grimuárn Gringurduá Grulbrir Guahbpsaál Gukuà Gusses Guálehbehp Ihdksin Ihgern Ihgoàhguáhg Ihkeàhb Ihpeálfehp Ihtaáhdpsir Ilbchisehg Ildbris Ilfkalurd Ilfksol Ilmahm Ilsbor Iltulg Irbchorerp Irbsoulg Irdpsorsseás Irgarmsoà Irgbo Irmnoàl Irnprilbu Irnshonolg Irsuhkgrin Irtbrel Iàrtalf Iárfpsonohf Kaerg Kahsir Kalfol Kearmtral Kehpa Kelpsaschun Kerkson Kernaáilm Kerteh Kiaht Kilohsfrul Koiàrmme Kolorb Korssuàn Kortuh Kossin Krargel Kraspohers Krenkarse Krimprir Krirchessa Krunkilsu Krurssar Ksalelm Ksaluhpsson Ksamahkelp Ksassuruhp Ksaàlpsis Kselihpalt Kseloáhn Ksemfroástrur Ksenaárfpoàr Ksestheluàln Kseámduhpses Ksinssuàr Ksiárthal Ksiásterchil Ksoásfirchim Ksulsiár Ksurulm Ksuschurilp Kupathos Kuse Machos Maeàhf Malksaánmeà Meábi Milpa Mirthur Miàhgouhf Mosifeà Mualkgril Mubeàsar Mutharohk Naframalt Nahfel Nasherga Nihfraàs Niilmehn Noaárdsil Nohsirelk Nuiàltuhp Nukruàsirk Ohdarn Ohkthemprim Ohmahgthel Ohmaht Ohmels Ohmshol Ohnkrun Olbbilihg Olgohm Olgoldper Olpki Olptulfraàl Orfalp Orfgoáh Orfthim Ormchimoálg Ortgekil Oàlgarg Oàrddatras Oàrpfrulbir Oáhgmi Oárdprun Oársulg Paaàrkuhd Pahkrirtal Pahnal Pebehdo Pelnor Perbi Pershes Peàiln Pohchir Poohmpsim Porirtfrar Porshol Possur Prinfeh Prolbehfeáh Promeàrt Prompelpsum Prorthimiáhg Prunbrumirk Psamsolpeàh Psarulkdrir Psaspsoálba Psaàlarnnuh Pserniáiáhf Pseásmo Psinilmpsaás Psirsseár Psisorb Psiámolf Psolfras Psorirggrem Psosoálg Psunird Psurilt Psussererf Puàroht Sacheásirp Safur Sahthomfros Saksuámshan Salge Salssungel Saltren Sashonssur Serfaá Sessul Shaltuurf Shamurkehn Shanfi Shaàrerbssim Sherthen Shesalp Sheálchir Shilksel Shinfrin Shirdil Shirurners Shiselk Shisiàlpseàr Shisksum Shisorbte Shiàmelbkoh Shiálbi Sholshuàn Shommor Shonbukur Shoniàlsssen Shoraáldchun Shorpa Shoànirk Shoàrers Shoásthuski Shumksulpe Shumpsuáralf Shunarm Shunkranshin Shunsi Sigasih Silguàmah Sinuils Situ Siuhb Sohpo Soàrkrasbaà Ssalals Ssalerfehg Ssalsa Ssalssinchas Ssamksemtroàm Ssardaohd Ssarehtirk Ssasterdo Ssernalaàhs Ssesert Ssirkaárgu Ssirpsol Ssischelkren Ssiàndekrar Ssiàneálm Ssomshuán Ssonertches Ssonksunshor Ssonpren Ssontrun Ssorgi Ssosgaál Ssoàmurd Ssulfeahm Ssurelkda Ssurshor Sudeh Tehilb Temerihf Terpsoár Teàrchim Thaltror Thantrespral Tharpaiáhb Thilbol Thirpsusolg Thiámku Tholahp Tholuhb Thomdal Thuldronilt Thulerkkser Thunaáhnsham Tigrul Tirdohfren Tissam Toeárm Toleáhsgrin Toluhb Tothosti Toárurb Trolfoh Tronkserki Trosshin Troánorb Trumild Trunpo Trurdrelelm Trurseh Trusohperm Tubolssom Turshos Tuàhbreàn Uhbdo Uhbolm Uhdohs Uhkald Uhpalm Uhpkros Uhpma Uhssseselk Uhtniulg Uhturf Ulbardeht Uldald Uldkeohf Ulkold Ulkteh Ulmbrir Ulnmimil Ulpehgilg Ulperb Ulppselthim Ulsalm Ulsseulk Ultma Ultmerchel Urkgoeálm Urkksiám Urkparolf Urmkoahp Urnsoohn Ursiáhdors Uàldgarorm

[innerdreamercollective]

Wedding the Wide Receiver by Lisa Suzanne is now live in audio!

Narrated by: Tor Thom and Kelsey Navarro Foster

A steamy Football, Marriage of Convenience, Sister’s Ex romance from Amazon Top Ten Bestselling author Lisa Suzanne.

I’m not really sure how I ended up married to my sister’s pro football player ex-fiancé, but my vicious hangover might have something to do with it.

It slowly comes back to me.

My family vineyard. A secret clause in my grandmother’s will. An allergic reaction. Benadryl. Way too much tequila.

And a wedding gown meant for someone else to wear in just a few days.

If I can get him to stay married to me for the next year, the vineyard will be mine, and my backstabbing sister will get exactly what she deserves…absolutely nothing. After that, we can go our separate ways and never speak of this drunken mistake again.

Except for me, wedding the wide receiver might be the best mistake I’ve ever made. Now I just need to get him on the same page so we can rush toward our happily ever after.

Listen today!

Audible: https://geni.us/WTWRaudible

Amazon: https://geni.us/WTWRaudio

Apple: https://bit.ly/3B4pJTb

Goodreads: https://bit.ly/4e86ebb

[anitabyars]

Playboy

by Marni Mann is now live! The

A sizzling, grumpy-sunshine, boy-obsessed, one-night-stand romance from USA Today best-selling author Marni Mann …

Spade. People know what to expect when they hear my last name.

Billionaire. Alphahole. The forever bachelor. Heir to Spade Hotels, one of the most luxurious brands in the world.

Want to know what they would never call me?

Boyfriend.

Until her.

With one glance at her in the club, I’m ready to claim her for the night.

Dark, flowing hair. A smile that causes my heart to pound. Eyes that pierce my soul. And a perfect body that makes every part of me pulse.

She’s addictive. Electrifying. Consuming.

I’ve never wanted anyone more.

Our eyes meet, but she looks right past me. She isn’t here for me. She’s here for the music.

For the first time in my life, a woman makes me work for it. Her indifference fuels the fire inside me.

The result? One night. No names. No introductions.

Just pleasure.

The way I’ve always liked it.

But now, I find myself fantasizing about this gorgeous stranger, and I swear I can still feel the softness of her skin and taste her on my lips.

The minute I saw her, a switch flipped inside me. Now, how do I stop this raging … obsession?

When our paths cross again in the most unexpected way, I’m on a mission to make her mine. But what happens when she wants nothing to do with me?

Download today or read for FREE with Kindle Unlimited

https://geni.us/leXbc

Audio Narrated by: Savannah Peachwood & Tor Thom

Goodreads: https://bit.ly/3OybFED

Meet Marni

USA Today best-selling author Marni Mann knew she was going to be a writer since middle school. While other girls her age were daydreaming about teenage pop stars, Marni was fantasizing about penning her first novel. She crafts sexy, titillating stories that weave together her love of darkness, mystery, passion, and human emotions. A New Englander at heart, she now lives with her husband in Sarasota, Florida. When she’s not nose deep in her laptop, working on her next novel, she’s scouring for chocolate, sipping wine, traveling, boating, or devouring fabulous books. 
Want to get in touch?

Connect with Marni

Facebook: http://bit.ly/MarniMannFB

Facebook Group: https://www.facebook.com/groups/1597153177180837/

Instagram: http://bit.ly/MarniMannIG

Pinterest: http://bit.ly/MarniMannPin

Amazon: https://amzn.to/2IsSRWC

Bookbub: http://bit.ly/MarniMannBB

Website: http://marnismann.com

Goodreads: https://www.goodreads.com/author/show/5400988.Marni_Mann

Verve Romance: https://ververomance.com/app/marnimann

TikTok: https://www.tiktok.com/@marnimann

Sign up for her newsletter: http://marnismann.com/newsletter/

[cocktailsfairytales]

P. Rayne continues the Midnight Manor series with Shattered Vows, a dark contemporary romance reimagining of Rapunzel, complete with gothic vibes.

Shattered Vows by @authorprayne is now LIVE!

Download today or read for FREE with #kindleunlimited 

https://books2read.com/svpr

Duet Narration by: Tor Thom & Muffy Newtown

Add to Goodreads: https://bit.ly/4bDsJnl

#prayne #midnightmanor #shatteredvows #darkromance #forcedproximity #valentineprlm @valentine_pr_