#Riemannian metric

[max1461]

california bans riemannian geometry because it is kinda white supremacist to put a metric on a manifold. florida bans topos theory becuase grothendieck was Woke

[positively-knotted]

Dissertationposting 3 - The Torus

Remember that last time, by taking f=1 in Lemma 1, we showed that ʃR_Σ ≥ ʃR for a stable minimal hypersurface Σ in a manifold (M, g). In particular, if R > 0 on M, so is ʃR_Σ. But if M is 3-dimensional, then Gauss-Bonnet says that Σ must be a union of spheres! Combining this with the fact that we can find a stable minimal hypersurface in each homology class of T³, this shows that T³ cannot have a geometry with positive curvature! Let's introduce some notation to make this easier - we'll say a topological manifold is PSC if it admits a metric with R > 0, and non-PSC else. Gauss-Bonnet says that the only closed PSC 2-manifolds are unions of spheres, and we've just shown that T³ is non-PSC.

How could we make this work for higher dimensions? Well, we can still write each torus as Tⁿ×S¹, so an induction argument feels sensible. In particular:

T² is non-PSC by Gauss-Bonnet

Every (Tⁿ, g) has a stable minimal T^{n-1} by taking the homology class of the meridian by Lemma 2

Stable minimal hypersurfaces in positively curved spaces are PSC?

By induction and contradiction, Tⁿ is non-PSC for all n.

So, what do we have and what do we need to prove Statement 3?

We need to allow (Σ, g) to not have R > 0 even if Σ is PSC. The easiest idea here is to find a function to scale g (ie distances) by to get a new metric.

If we scale by φ^{4/(n-2)}, then the new curvature is φ^{-(n+2)/(n-2)} Lφ, [1] where L is the conformal Laplacian

which is a reasonably well known operator that sometimes has nicer behaviour than the regular Laplacian.

To use the full power of Lemma 1, we want another result relating the integral of |∇f|² to Vf² for some other function V.

As if by magic, functional analysis gives us exactly the result we need.

Lemma 3.

Let (M, g) be a compact n-manifold, possibly with boundary, and V a smooth function on M. Then the infimum

is attained by some function φ. Furthermore, φ > 0 on int(M), and

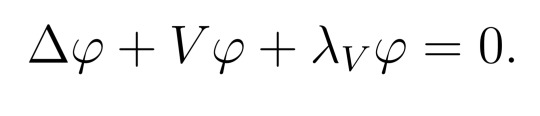
The proof [2] is pretty technical, but if you've done a course on Fourier analysis, the term "first eigenfunction" for φ might ring a bell. If you've done any undergrad course on ODEs, you can try thinking about how this relates to the normal existence theorem and maximum principle for the Laplacian (set V=0).

But that's all we need! Letting V = -(n-2)/4(n-1) R, Lemma 3 gives a function φ > 0 and constant λ with Lφ = -λφ; Lemma 1 and being careful with compactness gives that λ > 0; so scaling by φ^{4/(n-2)} does the job! It's worth recording that separately I think.

Proposition 4.

Let (M, g) be a closed manifold with R > 0. Then any closed stable minimal hypersurface is PSC.

Next time, we'll see how far we can push this method - in particular, it will turn out that we only actually care about the cohomology ring of M! I might even drop my first novel result, the classification of so-called SYS 3-manifolds.

[1] I'm not gonna do this for you, it's a direct calculation. I even gave you nice coefficients! I also think it's an exercise in Lee.

[2] This time, we pass to the Sobolev space H¹, where a sequence of functions approximating the infimum converges to a continuous function attaining the infimum. Showing it's an eigenfunction is fairly standard (vary φ, differentiate, divergence theorem), but the argument that it's smooth is cute. If Vφ + λφ is continuous, so is Δφ. But then φ is twice differentiable, so by induction smooth. Thierry Aubin's "Some nonlinear problems in Riemannian geometry" has all of the painful details, and a sketch is below.

[lovelanguageisolate]

I'm actually kind of spooked by machine learning. Mostly in a good way.

I asked ChatGPT to translate the Christoffel symbols (mathematical structures from differential geometry used in general relativity to describe how metrics change under parallel transport, which I've been trying to grok) into Coq.

And the code it wrote wasn't correct.

But!

It unpacked the mathematical definitions, mapping them pretty faithfully into Coq in a few seconds, explaining what it was doing lucidly along the way.

It used a bunch of libraries for real analysis, algebra, topology that have maybe been read by a few dozen people combined at a couple of research labs in France and Washington state. It used these, sometimes combining code fragments in ways that didn't type check, but generally in a way that felt idiomatic.

Sometimes it would forget to open modules or use imported syntax. But it knew the syntax it wanted! It decided to Yoneda embed a Riemannian manifold as a kind of real-valued presheaf, which is a very promising strategy. It just...mysteriously forgot to make it real-valued.

Sometimes it would use brackets to index into vectors, which is never done in Coq. But it knew what it was trying to compute!

Sometimes it would pass a tactic along to a proof obligation that the tactic couldn't actually discharge. But it knew how to use the conduit pattern and thread proof automation into definitions to deal with gnarly dependent types! This is really advanced Coq usage. You won't learn it in any undergraduate classes introducing computer proof assistants.

When I pointed out a mistake, or a type error, it would proffer an explanation and try to fix it. It mostly didn't succeed in fixing it, but it mostly did succeed in identifying what had gone wrong.

The mistakes it made had a stupid quality to them. At the same time, in another way, I felt decisively trounced.

Writing Coq is, along some hard-to-characterize verbal axis, the most cognitively demanding programming work I have done. And the kinds of assurance I can give myself about what I write when it typechecks are in a totally different league from my day job software engineering work.

And ChatGPT mastered some important aspects of this art much more thoroughly than I have after years of on-and-off study—especially knowing where to look for related work, how to strategize about building and encoding things—just by scanning a bunch of source code and textbooks. It had a style of a broken-in postdoc, but one somehow familiar with every lab's contributions.

I'm slightly injured, and mostly delighted, that some vital piece of my comparative advantage has been pulled out from under me so suddenly by a computer.

What an astounding cognitive prosthesis this would be if we could just tighten the feedback loops and widen the bandwidth between man and machine. Someday soon, people will do intellectual work the way they move about—that is, with the aid of machines that completely change the game. It will render entire tranches of human difference in ability minute by comparison.

[fump-2]

I feel like if my professors utilized balloon animals in their lectures I would be more able to recall what was discussed.

Riemannian metrics? That was the professor building a panda in front of us.

[cherrynika]

I handed in my DG assignment (question 1, prove that the tangent bundle of a smooth manifold is always orientable... and that was like the easiest question) and now have three weeks of tensor bundles and riemannian metrics to catch up on. Before I get started preparing for the tutorial on Anal 1 (analysis 1 to the un-enlightened) that I have to teach tomorrow, I decided to read the Logan Sargeant article in GQ. It smelled incredibly fishy... like a product placement. The product is Logan himself.

So, I am going to write another version of it that gets straight to the point.

original article is accompanied by sexy photos

so if you think that logan is sexy you may enjoy them.

Below the cut. Meet Logan Sargeant, America's Great F1 Hope

translation : Meet Logan Sargeant, America's Great White Hope

Logan Sargeant is a 22-year-old American male. He has blonde hair, light eyes, a square jaw, and the sort of glinting crooked grin that will prove a threat to safe-feeling boyfriends on the several continents where F1 runs. translation: He's WHITE. Please think that he is hot.

While sitting in the living room of Mario Andretti last spring, I asked him about the prospect of a full-time American F1 driver in the near future, and he responded with a story that has stuck with me. About a decade ago, he said, he visited the Red Bull factory in England, and asked Red Bull team boss Christian Horner about some young American prospects: “And the rebuke I got was unbelievable,” Mario told me. “He said, ‘You know if you bring an American driver here, we’ll destroy him.’”

translation: He's disadvantaged by the mean Europeans for being Americans. Please support this smol bean.

But could an American driver overcome the biases by committing to their system and winning on their soil? When Logan left Florida for Europe after elementary school, he made that commitment all the way—and hasn’t really been back to the US to race since.

translation: look at the sacrifices he made by leaving the land of no human rights to go and stay in switzerland

Sargeant doesn’t fit neatly into any of those categories, but his uncle is a billionaire, and his ascent to the summit of international racing did begin with a rich-kid Christmas present. Neither parent ever raced cars, but Dad decided to get the boys go-karts one Christmas because Mom didn’t like the dirt bikes they were riding. “It was honestly just about finding a new thing to have fun with,” Logan said. Five-year-old Logan and eight-year-old Dalton started taking their go-karts out to the track at Homestead and Opa Locka, just a weekend thing at first. But they got hooked. And each steadily overtook the competition in Florida and the Southeast. Win after win. “And so it was: OK, now what do we do to make it harder?”

translation: This is a rich person sport, which you are aware of. Logan is rich, we can't hide it because his family is in the billionaire class and has deep involvement in the murky politics of the America including bribery and uh, other stuff, that we will discuss. But um his family was not THAT rich. You can still feel good about rooting for him! He's not just an American Stroll/Latifi or good FORBID an American Mazepin

Logan finished up fifth grade in Florida while the family made their move to Switzerland. In addition to the racing opportunities, Dad had business there. (Dad’s company, it should be acknowledged, was taken to court a few years ago by the US Government for bribing officials in three South American countries to secure asphalt contracts. The company pleaded guilty and agreed to pay over $16 million in fines.) In Europe, Logan quickly began ascending through the ranks, traveling throughout mostly Italy to karting races on weekends. “I definitely felt like school was a lot more challenging than in Florida,” he recalled. “And we were missing a lot of school, for sure, but that’s part of it with racing. It is what it is.”

translation: ok. Yes, we admit it, the Sargeants are wealthy. And his father's company has been bribing government officials in South America and are doing such a large volume of business that they paid 16 million in fines. But let's just skip over that part. It's not really that important. The important part is that this young man who was financed by dirty money is just SUCH a young man and deserves your attention. Look, he missed school to race, look at his passion!

“We’ve been searching—in a little bit of a ditch trying to find out what we can do,” Logan told RACER in February 2021. “Try and find something in sports cars or I’d even consider Indy Lights [the support series of IndyCar]—that’s a really cool option.” Here he was, just two years ago, mapping out his retreat from formula racing in Europe with the press. Openly musing about his prospects in the lower ranks of American racing. The article that featured those quotes put an even finer point on things: “Logan Sargeant will not step up to Formula 2 this season and is unlikely to remain on the FIA path to Formula 1.”

translation: He almost missed the chance to be in F1.

But maybe that encounter with Pitt last year was even more meaningful to Sargeant than he even realized. Maybe those side knuckles were a blessing of sorts, an off-loading of expectation, a transference. Maybe it was Pitt communicating to Sargeant that he needn’t carry the weight of the sport in America alone, because he, Brad Pitt, would help do it instead. At least for a little while. Hollywood could take the spotlight while Logan Sargeant found his feet, clocked his hours in his race car, and proved himself to be the glorious mid-pack F1 driver we all know he can be.

translation: He's carrying all of America's hopes and dreamz

[nimblermortal]

All right I no longer remember why I was reading about de Sitter space, but I’m getting into a Wiki hole so I’m taking some notes here.

1. “In mathematical physics, n-dimensional de Sitter space (often abbreviated to dSn) is a maximally symmetric Lorentzian manifold with constant positive scalar curvature”

2. A Lorentzian manifold is a type of pseudo-Riemannian manifold

3. “In differential geometry, a pseudo-Riemannian manifold,[1][2] also called a semi-Riemannian manifold, is a differentiable manifold with a metric tensor that is everywhere nondegenerate.”

4. “In mathematics, a differentiable manifold (also differential manifold) is a type of manifold that is locally similar enough to a vector space to allow one to apply calculus.”

5. “In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point.” 

5. This is actually a sentence that makes sense to me, but in case it doesn’t to you: a Euclidean space is basically the sort of space that you’re thinking of with points on a graph. It’s regular, it’s even, it’s got a consistent coordinate system... A non-Euclidean space is, say, if you’re trying to project the Earth onto a map. Even assuming the Earth is perfectly round, trying to get that onto a flat plane leaves you with vastly irregular spacing and, well, all the flaws of the Mercator projection.

So a manifold is a shape, in n dimensions, such that any point on it looks like the space around it is Euclidean, but if you zoom out a bit further it ain’t. “One-dimensional manifolds include lines and circles, but not lemniscates.“ - a lemniscate ~is a figure 8 or an infinity symbol. On either side of the intersection point, it’s basically a circle and works as a one-dimensional line or circle, but at that intersection point, you have to have two dimensions (n+1) to describe the intersection of those lines, so it no longer locally resembles a 1-dimensional Euclidean space at that point.

4. A differentiable manifold is one that you can work calculus on. (I’m going to assume you remember scalars and vectors. If not, a scalar is a number, a vector is a number with a direction, or in graphical senses a ray.) I’m not... super clear on why you need a vector space to work calculus, but then, I’ve always tried to forget visual representations of math as fast as possible because I am a hugely non-visual person and they just confuse me. So it probably has something to do with that, and the way integration represents the area under a curve and differentiation represents its... na, slope or inflection point or whatever.

3. “In the mathematical field of differential geometry, a metric tensor (or simply metric) is an additional structure on a manifold M (such as a surface) that allows defining distances and angles, just as the inner product on a Euclidean space allows defining distances and angles there.”

The inner product is the dot product, fyi. If that doesn’t make sense to you... I’m not explaining it here. Sorry if that’s rough, but ultimately I am here for my own understanding and that’s a whole class on matrix arithmetic. Suffice it for here that the inner product lets you take your matrix representation of two curves, do math to them, and come up with a scalar representation of their relation. The metric tensor here is the generalization of that concept, something that lets you define curves’ relationship to each other.

(Note I am using the word ‘curve’ to represent lines and scribbles with arcs, consistent or not.)

“In mathematics, specifically linear algebra, a degenerate bilinear form f (x, y ) on a vector space V is a bilinear form such that the map from V to V∗ (the dual space of V ) given by v ↦ (x ↦ f (x, v )) is not an isomorphism.”

So a non-degenerate metric tensor is one such that the map from V to V* IS an isomorphism. Note that if I am remembering correctly, v is a vector in the space V. I had to remind myself that the dual space is like. Every vector that can exist in V? if you do basic mathematics to them? (Note that I am using phrases like ‘basic mathematics’ very broadly and in a not mathematically-approved sense.) And of course f(x) is a function. And an isomorphism is something that can be reversed with an inverse function.

So then x maps to f(x,v), and v maps to whatever ray or space that original mapping defined, and you can’t undo that. Except that we’re talking a non-degenerate space, so in fact the pseudo-Riemannian manifold that we started out talking about is a manifold (point 5) on which you can work calculus in a way that enables you to describe directions and angles and reverse functions/mappings done in that space. (I am much less confident in that last point.)

That brings me through point 3, but now I have to sleep.

[imperiumallaboveall]

Eigenvalues and eigenvectors - Wikipedia

White hole

Lorentzian manifold is an important special case of a pseudo-Riemannian manifold in which the signature of the metric is (1, n−1) (equivalently, (n−1, 1); see Sign convention). Such metrics are called Lorentzian metrics. They are named after the Dutch physicist Hendrik Lorentz.

[laurazukerman-blog]

Riemannian Geometry

Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, defined as smooth manifolds with a Riemannian metric. This gives, in particular, local notions of angle, length of curves, surface area and volume. However, there are many natural smooth Riemannian manifolds, such as the set of rotations of three-dimensional space and the hyperbolic space, of which any…

[liegroups]

Will the exam involves contents of the differential geometry further than smooth manifolds, submanifolds, smooth maps, tangent spaces, vector fields, flow/integral curves of vector fields, differential forms, integration with differential forms, immersions and submersions, as described in the prequisites? For example, the Riemannian manifold, which occured in hw 8.

The exam will stick to the prerequisites as you list. Riemannian metrics etcetera were only there for the purpose of a particular exercise.

[transgenderer]

@tanadrin said:

i wanna hear more about how the lines and angles are fucked up

okay so for general pseudo-riemannian manifolds like whatever can happen. but for minkowski space, which Ps-Riemanifolds approximate locally, we can talk about what happens. and its fucked

so actually i guess lines are pretty nromal. BUT it's not a metric space, because distances can be 0 (between distinct points), or negative. like there's a whole double cone of points "0 distance" away from a particular point. and instead of angles, you have rapidity. the fundamental weirdness of trying to think of minkowski space "geometrically" is that from this perspective it's anisotropic, one of the directions is special. so instead of angle between two lines, it's like...their relative velocity, is the angle. which is kind of like angle? sort of? but its anisotropic. also its hyperbolic

egan's dichronauts is set in a world where one of the space directions is timelike, and it gets crazy, especially the physics

In the grand tradition of mathematicians using the word trivial in a way whose meaning is deeply ambiguous, I think there's a meaningful sense in which 3 dimensions is "the lowest nontrivial dimension". Now I hear you saying isn't that two dimensions (obviously 1D is trivial. No geometry) and look 2D is cool and all but it is not that rich geometrically. I think if we were 4D beings we would still think that 3D is the lowest nontrivial dimension. However we'd be so high on being able to do complex analysis intuitively we wouldn't even care about geometry. Fuck 4D beings. Also you could say we ARE 4D beings cuz time but if you consider us as living in a 4D manifold it's not even riemannian it's PSEUDO riemannian. Which if you're not a math person: the notion of "straight line" and "angle" is all fucked up. Very unlike Euclidean space. Don't wanna go there

[positively-knotted]

Dissertationposting 2: Curvature & Hypersurfaces

(Note: I'm not gonna say anything about what I mean by "curvature", as if you haven't already seen it in some context I don't think you're gonna get much out of these posts :/. But for clarity, I'll only ever talk about scalar curvature and call it R. If you're used to Gaussian curvature written K, this is the same except R = 2K. Oh also all my manifolds are oriented.)

It may not be immediately obvious why we would want to consider hypersurfaces when trying to understand curvature - after all, R³ is flat, but contains surfaces with all kinds of curvature. So a motivating example may be in order. This is in fact the example that spurred all of the developments we'll talk about, and is of particular importance in theoretical cosmology! Maybe I'll say more about that later.

Consider a manifold homeomorphic to the n-torus Tⁿ - or more properly, Tⁿ with a choice of geometry (Riemannian metric). Intuitively, this shouldn't be able to have R > 0 everywhere, in the same way that T² can't. Proving this is surprisingly hard, but one sensible approach would be to try induction. After all, T³ is just T² × S¹, and S¹ is easy to understand. Thought of the other way around, we want to find nice hypersurfaces and do inductive descent until we reach dimension 2, then apply Gauss-Bonnet.

But if any old hypersurface doesn't say much, what about particularly nice ones? The obvious candidates are so-called stable minimal hypersurfaces. These are minimal points for area, in the sense that if you perturb them very slightly, their area must increase (e.g. the meridian of a standard torus in the motivating example). The big result about these is as follows:

Lemma 1.

If Σ is a stable minimal hypersurface in a manifold (M, g) and f is any function on Σ, then [1]

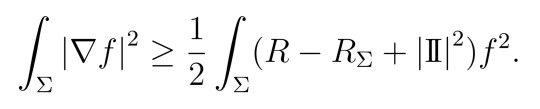
Here the left side is the gradient of f (in the normal calculus sense), and \II is the second fundamental form, a number that tells us something about how Σ sits inside M. You can think of it as a kind of error term, but the important bit is that it's squared, so non-negative. R is the scalar curvature of the ambient manifold M, and R_\Sigma is the induced scalar curvature of Σ.

You've probably never seen this before, even if you've done differential geometry. I don't know why this formula isn't better known, it's super useful, as with clever choices of f it gives big results. Just taking f=1 shows that for a stable minimal hypersurface, the intrinsic curvature has to be greater on average than the external curvature. This is a pretty big step forward!

Ok, so we have our choice of useful hypersurfaces. Now we just need to show that they always exist. And they do! In fact, they exist for each homology class:

Lemma 2.

Let (M, g) be a closed n-manifold, 3 ≤ n ≤ 7. Then for any class α ∈ H_{n−1}(M), we can find a closed stable minimal hypersurface Σ such that [Σ] = α in homology.

Let's unpack this a bit. We can think of hypersurfaces as living in a particular homology class in the usual geometric way. It's a standard result from differential topology [2] that we can in find a hypersurface living in any homology class, and that slightly perturbing it won't change that class. The interesting bit here is that we can always take a stable minimal representative, in sufficiently small dimensions. [3] Annoyingly, this means everything from here on out only applies in dimensions less than 8, even though there's no good topological reason why it isn't true more generally. (It definitely is true more generally, we just need a stronger version of this lemma and that makes it an analysis question.)

Next time, we'll use this to show that Tⁿ doesn't admit positive scalar curvature! Notes below the cut.

[1] Proof of Lemma 1. Start with the usual Gauss equation. Take the trace to pass to Ricci curvature, then again to pass to scalar curvature. It turns out that the irritating terms from varying dimensions cancel out! More detail in the screenshots below:

[2] Remember that there is a bijection between H¹(M) and homotopy classes of maps M -> S¹, pairing [f] with f^*(ω), where ω generates H¹(S¹). We can assume f is smooth, choose a regular value t, and set Σ = f^{-1}(t). Then [Σ] is Poincaré dual to f^*(ω).

[3] The actual argument here is pretty standard for the analysis I'll be omitting. In general, if we want to show that an object in space X with property P exists, we'll pass to a bigger space Y where standard results give us an object with that property; then somehow argue that P implies that it's actually of type X. Here, we pass from submanifolds to currents, and minimise area for currents in a given homology class. By measure theoretic magic, this minimisation forces the singular set of the current to have codimension at most 7, so in dimensions less than 8 it is in fact a submanifold.

[math-memes]

[godelitonthemountain]

I was thinking that this might work is semi-riemannian manifolds. This doesn't work in a normal metric space because the metric has to be positive-definite but with that removed it could work. It would basically be like saying that any directions where the metric signature of a manifold is negative have their coordinates "multiplied by i" and the distance function, instead of having negatives, would use the i's in the coordinates to make the terms negative.

Like for Lorentz space-time you could say that your position is x+it instead of (t,x) and use the normal euclidean distance function.

a right triangle with a hypotenuse of 2 and legs of lengths √5 and 𝑖

complex distance is a kinda funky concept and even "normal" higher-dimensional space doesn't allow it but aside from that this... could work? just gotta come up with a coherent distance metric that allows for complex distances and where the pythagorean theorem still applies

[tempenensis]

Jujutsu Kaisen : Abyss of Math Course - part 2

(Continue from Part 1)

Sonoda (S): There’s also a way of thinking that in the application, the distance shrinks and stretches, for example, if we apply Riemannian manifold in the space, we can define ds distance of neighboring points and the ds will stretch. This way of thinking is also not wrong. The specific form of Riemannian manifold is, for example, can be decided by kernel function.

Takano (T): The ds here is the distance between the two of curse users, right?

 S: Yes. Depending on the place, it’s like the density of the ruler has changed. By doing that, it will feel like the distance per unit grows. The way it can expand and contract is like a metric conversion, there are various types of them, but information geometry and conformal transformation (=conformal symmetry) are used a lot. But I don’t actually know (laugh).

T: Wait, wait. Let’s summarized it a bit! The ruler here has certain distance per unit. Just for example, let’s make the length of unit 1 m.

Hino (H): OK. If we use the kernel concept, no matter how much value of the variable within, you can tweak it. In short, it seems like this… ? (Board 3)

S: Let’s think that we live in a world where Gojo does dx of 1 m ruler length between him and his enemy, causing this ruler to be distorted, and it turns to be ds. From his point of view, because of this distorted ruler, for example 10 m can become |ds| = 1 depending on the location.

T: I see! So, based on this, even if someone runs 10 m, it would look like they only advance forward “1”.

H: Exactly. Like this, the range is getting longer and longer.

T: I’m certain that by doing this, then it will look like they forever can’t reach him.

H: On top of that, by using his technique, Gojo can make the distance per unit when (someone) getting near to him feels like it becomes larger.

S: That’s why you can design when they are getting closer to him, they feel like they are getting so much slower.

T: True!

H: With this, I think we can somehow define “Blue”. (Board 3)

(Board 3)

cont’d under the cut.

T: Then, next is “Red”.

S:  “Red” is the reverse of “Blue”, if we write it as transforming the measurement of space, I think it’s fine to assume (Red) reversing the direction of the ruler.

T: It certainly is. By doing that, |ds| = 1 of this time, if someone is getting near Gojo, the subject feels that he is nearer. For example, if it’s seen from outside, the distance is actually 1 m, but the subject feels like it has become 1 mm. Then suddenly they are blown away! (Board 4)

H: This topic in our field machine learning actually close to the method of “distance learning”.

T: I can remember a few things. For the sake of readers, I will try to explain this “distance learning”. For example, there are 2 elephants and a dog here. There is a big elephant and a small elephant. The big elephant is 5 m long and weighs 5 tons, while the small elephant is 1 m long and weighs 4 tons. On the other hand, the dog is quite big, it’s 0.5 long and weighs 0.05 tons (Board 5). In this case, if the distance is simply the total difference of body length and weight, the difference of small elephant and the big dog is (1-0.5) + (4-0.05) = 4.45 while the difference of the big elephant and small elephant is (5-1) + (5-5) = 5; with this we can see that the distance of the small elephant and the dog is the closer one. This is because we thought about their weight in tons. If we calculate the weight in kilogram, then the distance of the big elephant and the small elephant becomes the closer one instead. The topic of automating this kind of process into the machine (computer) is called “distance learning”.

H: Yes, yes, it’s method to “weight” “which scale you want to emphasize”. Takano-kun’s example looks simple, but it is only sometimes used for distance calculation between the same image, the same music or the same products; by doing it like this, we can apply recognition and recommendation to see is this music similar, or is this image similar.

T: I’ve been in this company for 5 years, my memory has gone (laugh). To think the day has come where I am placed in Jump…

(Board 4) By considering that “Red” is the reverse of “Blue”, this time getting near (to Gojo) means that the distance is getting farther. It is like the illusion of being blown away at tremendous speed.    

(Board 5) Originally the big elephant and the small elephant are “elephant” the same, so the distance must be closer. But depending on the emphasized unit and scales, the result may change. 

S: So next, let’s try thinking something that seems to match. “Purple” is written as the mix of “Red” and “Blue”.

H: As expected, it’s “void” formula. (Akutami-sensei) wants to use imaginary number, right? So do we stop using Euclidean weighing, and use Minkowski weighing and Koehler manifold instead?

S: The norm is that they are used at the same time, but because it’s a complex domain, it will look like “So you came from that point”.

H: Ahaha (laugh).

T: I completely don’t understand what the two of you are excited about (laugh).

H: Back to the topic at hands, the direction from me going to Takano-kun and the direction from Takano-kun to my location have changed, you can think it like KL divergence.

T: That’s one of the basics of information geometry, right? Because we think of the distance based on each other’s standard, the value changes based on whose point of view, it’s asymmetric distance.

H: Right! That’s why the distance when Gojo sees his enemy and when his enemy sees Gojo is different. No matter how Gojo’s technique applies these concepts, “Blue” and “Red” can be established.

T: Because there are two theories, let’s adopt the first one. 

Conclusion

Using the Limitless cursed technique “Red” and “Blue”, Gojo can do conversion and change the scale of distance between him and his opponent.  

(to part 3)

[nostalgebraist]

[post about high-context trivia]

For practical reasons, I’ve been reading papers recently about minor architectural details in transformers.

People mostly vary these things to make training more stable, rather than for final performance, which barely cares about the architecture (e.g. you can do GPT-2 with only 6 layers, maybe only even 2, if you make it wider to compensate).

Here’s an example paper that cites a lot of the others.  These papers are mostly about the placement and function of the layer norm operations -- for example it helps a lot if you move them so they don’t block the residual connections from working as intended (“pre-norm”), which they did in the original transformer (“post-norm”).

This made me think about layer norm again, which had always bothered me, because it’s not coordinate invariant!  I had figured “oh it probably doesn’t matter” but apparently you get better performance if you remove the part that is not coordinate invariant (“RMSNorm” and “ScaleNorm”), so maybe the coordinate invariance is harmful.

Layer norm is weird and I don’t understand why it got off the ground in the first place.  It’s an operation that takes in a vector, subtracts off its “mean,” and then scales the result to unit norm.  What is the “mean” of a vector?  Well, it’s the mean in whatever basis your computer happens to be using. 

This might be less bad if you imagine it being applied rather after the activation function, which selects a particular basis anyway (and layer norm would operate in that basis).  However, in transformers it’s applied after embedding and projection steps that have no preferred basis.

When you think about what this actually does, it seems pointless?  Subtracting “the mean” is equivalent to choosing some direction and projecting out that component.  So, after layer norm your N-dim vectors will always live in an (N-1)-dim subspace; otherwise everything’s the same, so it’s similar to reducing your hidden size by 1.  (Though not exactly the same.)   I don’t see how this would stabilize anything.

Layer norm also does another thing in the preferred basis later, multiplying each component by a learned “gain.”  Not sure what this accomplishes.

The authors of the original layer norm paper try to justify it using information geometry (!) . . . I don’t know what to make of talk about Riemannian manifolds and metrics when you haven’t written a coordinate-independent function to begin with.

When used properly in transformers (“pre-norm”), it gets applied to the input of each residual branches i.e. when we compute x + f(x) we change it to x + f(LN(x)).  Among other things, this means there’s this one component of the input which nothing can see, but which is preserved all the way to the output through the identity branch.  In GPT specifically there’s another layer norm at the end, which will delete this component, so it just does nothing.  In other cases, it will affect the output logits, but the input is a learned embedding vector anyway, so this can’t matter much.

[jhavelikes]

Uniform Manifold Approximation and Projection (UMAP) is a dimension reduction technique that can be used for visualisation similarly to t-SNE, but also for general non-linear dimension reduction. The algorithm is founded on three assumptions about the data The data is uniformly distributed on Riemannian manifold; The Riemannian metric is locally constant (or can be approximated as such); The manifold is locally connected. From these assumptions it is possible to model the manifold with a fuzzy topological structure. The embedding is found by searching for a low dimensional projection of the data that has the closest possible equivalent fuzzy topological structure.