#L.E.J. Brouwer

[chrisengel]

Intuitionist totality is a fundamental concept in intuitionist mathematics that sharply contrasts with the classical approach. While classical mathematics embraces the law of the excluded middle—the principle that every statement is either true or false—intuitionism demands a more constructive framework. A set is deemed totally defined within intuitionism only when a concrete method exists to determine membership for any given element. This necessitates a specific procedure to prove whether an element belongs to a set or not. Intuitionism is profoundly skeptical of potential infinity, requiring that all set elements be individually specified or constructed. This constructive approach has profound implications for fields like analysis, logic, and set theory. As L.E.J. Brouwer, a pioneer of intuitionism, asserted, "The real numbers are not to be thought of as given in advance, but rather as continually becoming." This quote encapsulates the intuitionist view of mathematics as a dynamic process of construction. In contrast, David Hilbert, while critical of intuitionism, acknowledged its significance, stating, "Intuitionism is a serious attempt to establish mathematics on a new foundation."

[arehera]

Oh, don't worry, it already happened. The Nazis supported intuitionism, the idea that mathematical concepts should follow from acts of the human mind, against formalism, that mathematics could essentially be represented as a logic game with stated definitions manipulated through a series of rules to result in proofs. One example at the heart of the conflict was L.E.J. Brouwer's rejection of the principle of the excluded middle while David Hilbert, champion of formalism, accepted it.

The principle of excluded middle is so simple that you've probably used it a hundred times without noticing it. All it says is either A is true, or A is false. A third, middle option is excluded. So if we disprove not A, we have proven A. It's the basis for all proofs by contradiction, and Brouwer argued that because it required the mathematician to rely not on the existence of something they had constructed it could not be accepted.

This could have been a normal debate in the philosophy of mathematics, and still is. But Brouwer was at least neutral towards the Nazi party. According to Abraham Fraenkel (the F in ZFC) he was more than neutral and positioned himself as a "champion of Aryan Germanness." Under Ludwig Bierbach this went further. Intuitionism was declared proper German mathematics, while axiomatic formalism was "Franco-Jewish." Jewish mathematicians Landau and Noether were removed from positions at the University of Gottingen (as were physicists Szilard and Teller). Ironically, Hilbert, by that time in his 70s was also was also positioned as an exemplar of German mathematics despite his love for formalism and hate for antisemitism. When Nazi education minister Bernhard Rust asked him how mathematics at Gottingen was progressing after the expulsion of its Jewish staff he responded "There is no mathematics at Gottingen."

Intuitionism is not inherently fascist. There are many working intuitionist and constructivist mathematicians doing good work. But fascists are inclined towards intuitionism, rejecting the idea that mathematics exists outside the control of human thought. Their need to control everything extends to mathematics as well.

How long until it happens? Just long enough until a conservative politician reads a math textbook or some staffer has enough of a knowledge of math history to try this signal.

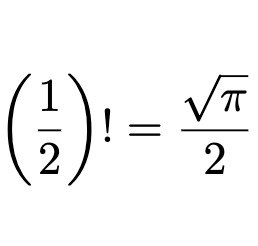
a thought that’s been floating around my head recently

conservatives like to parade around mathematical truths such as "2 + 2 = 4" as evidence that their social truths are fundamental and cannot be argued against

how long until conservative talking heads and/or annoying traditionalists find out about the esotericism and diversity of study in wider mathematics and start labelling it “degenerate mathematics”?

seriously. i wouldn’t be surprised if counterintuitive notions like “the factorial of one half is equal to half the square root of pi” are somehow a serious insult to a conservative’s idea of mathematics always being concrete and morally correct.

i mean, such an unintuitive idea kinda runs against a conservative philosophy that all truths are either self evident, or delivered by a higher power.

which i think ties into a wider misconception of higher mathematics being about adding things up - which is just not at all what it’s like, at all.

real, actual higher mathematics feels more like writing poetry than doing calculations, and i could make a whole nother post about that.

but all that most people know is times tables and sums. and i fear that if conservatives find out about abstract algebra, they’ll think it’s woke.

[haarlemupdates]

Persoonlijk archief van beroemde Nederlandse wiskundige L.E.J. Brouwer toegankelijk bij Noord-Hollands Archief

Persoonlijk archief van beroemde Nederlandse wiskundige L.E.J. Brouwer toegankelijk bij Noord-Hollands Archief

Het persoonlijk archief van professor Luitzen Egbertus Jan (Bertus) Brouwer (1881-1966), een van de grootste Nederlandse wiskundigen, is nu toegankelijk voor het publiek bij het Noord-Hollands Archief. Ter gelegenheid van dit moment, wordt er op 17 maart 2022 in de Janskerk in Haarlem een symposium omtrent deze befaamde wetenschapper georganiseerd. In 2015 is het persoonlijk archief van L.E.J.…

[thetwomeatmeal]

I've always thought that the mathematical community's rejection of intuitionism should be thought of as a choice -- not a bad choice but still one we could've made differently. It's not incoherent, and possibly not even as hard to work with as most of us seem to think. It just reflects different intuitions about what mathematical objects are and how they should be treated. So it's really interesting to see someone be explicit about this -- this guy is revitalizing part of Brouwer's ontology, which is related to a sort of idealized theory of mind, against the more popular Heyting position that intuitionism should be thought of as a variant logic.

[christian-dubuis-santini]

"Ceux qui sont dangereux, ce sont les hommes ordinaires, les fonctionnaires prêts à croire et à obéir sans discuter."

(Primo Levi - Si c'est un homme)

La dictature à prétexte "sanitaire" a accouché d’un cortège de mesures débiles, iniques, anti-sociales et contre-productives au plan strict de la santé, se motivant du prétexte de l’incapacité pour les hôpitaux de faire face à un afflux massif de malades, notamment dans les services de réanimation.

Sur les réseaux dits sociaux, on voit régulièrement passer un tableau chiffré avec: "tant de lits supprimés sous Sarkozy, tant de lits sous Hollande, tant sous Macron..." mais ce qui n’est jamais abordé, jamais évoqué, jamais questionné c’est: sur quelles bases ces mesures ont été — et continuent d’être prises? Réponse: la modélisation mathématique. Les mathématiques actuelles appliquées à la prévision sont imposées avec une arrogance que contredisent (entre autres) tous les principes de la mécanique quantique, qui démontrent que les événements chaotiques sont imprévisibles...

Voilà l’une des clés pour comprendre en quoi consiste l’idéologie des temps présents.

Ce "monde" n’est qu’un fantasme qui se soutient d’un certain type de pensée(s).

«…il faut quand même que je vous fasse sentir la portée d’une certaine façon dont moi je fraye la logique modale.

Le plus fort, hein, c’est que bien sûr, pour ce qui est de construire, pour ce qui est d’inventer…et voyez là tous les échos d’intuitionnisme qu’il vous plaira, si tant est que vous sachiez ce que c’est

…je vous ai traduit un jour le nécessaire par ce qui ne cesse pas de s’écrire.

Bon. Sachez-le, il y a une trace dans Aristote, que la logique propositionnelle… à savoir que quelque chose est vrai ou faux, ce qui se note 0 ou 1 selon les cas …il y a une petite trace, il y a un endroit où Aristote dérape - je vous montrerai ça quand vous voudrez - dans le Περὶ Ἑρμηνείας[Peri ermeneias] comme par hasard, De l’interprétation, pour ceux qui ne l’entravent pas –

il y a un endroit où ça fuse, que la logique propositionnelle est tout aussi modale que les autres.» (Lacan - Les non dupes errent)

Pour le psychanalyste, l’nconscient est ce qu’il y a de plus logique, la "Spaltung" ne passe pas entre le psychique et le somatique mais bien entre le psychique et le logique. Rien de plus logique qu’un psychotique...

Dans cet extrait des "non-dupes errent", Lacan lâche le mot d’"intuitionnisme"...

L'intuitionnisme (source Wiki) est une philosophie des mathématiques que L.E.J. Brouwer a élaborée au début du xxe siècle. Pour lui, les mathématiques sont une libre création de l'esprit humain et tous les objets qu'elles manipulent doivent être accessibles à l'intuition. L'intuitionnisme a pour conséquence une profonde remise en cause des mathématiques, notamment en refusant l'infini actuel: un nombre réel ne peut être représenté comme une suite infinie de décimales qu'à la condition de disposer d'un moyen effectif de calculer chacune de ces décimales; on parle alors de réel constructif.

Sur le plan logique, l'intuitionnisme n'accepte pas le raisonnement par l'absurde ou le tiers exclu pour la raison que ces principes permettent de démontrer des propriétés de façon non constructive: par exemple si on veut démontrer l'existence d'un nombre réel satisfaisant une certaine propriété, on peut raisonner par l'absurde, supposer qu'un tel réel n'existe pas, en déduire une contradiction et conclure que donc un tel réel existe, mais cette démonstration ne donne aucune indication sur la façon dont on pourrait calculer ce réel. Pour un intuitionniste on a juste démontré que l'existence d'un tel réel n'est pas contradictoire, mais pas que ce réel existe.

La logique intuitionniste a été développée par V. Glivenko et Arend Heyting, Kurt Gödel et Andreï Kolmogorov et formalise les principes logiques sur lesquels s'appuie l'intuitionnisme.

L'intuitionnisme est souvent considéré comme une forme de constructivisme, avec lequel il a beaucoup en commun, mais il s'en écarte quand, comme c'est le cas pour l'intuitionnisme originel de Brouwer, il conduit à des énoncés mathématiques valides qui ne le sont pas classiquement. La logique intuitionniste ne permet, elle, de démontrer que des énoncés valides en logique classique.

Voilà qui permet d’éclairer une partie des problèmes contemporains et notamment la colère de Didier Raoult contre le coup de force permanent des "méthodologistes" qui voudraient se faire passer pour "la Science" alors que la méthodologie n’est même pas une science.

Par exemple dans le pseudo-débat autour de la Chloroquine qui n’est en vérité que ’un enfumage idéologique ayant pour conséquence d’opposer deux types de rapport au langage et donc du sujet au réel, avec d’un côté:

– les partisans du médecin Didier Raoult qui avec son équipe a soigné directement cinq mille personnes infectées au coronavirus à Marseille, avec un taux de mortalité autour de 0,5%, et qui a fourni un suivi médical conséquent, avec toutes les études scientifiques afférentes, le docteur Raoult étant par ailleurs considéré comme l’un des plus grands infectiologues du monde, présentant un bilan réel, détaillé, argumenté dans les conditions réelles de maladie, de souffrance et de vie, et de l’autre côté:

– les tenants acharnés d’une version "Big Data", des geeks qui passent leur vie devant un ordinateur, dont les logiciels croisent des données (on les désigne aussi de l’acronyme MUM Mathématiciens Universitaires Modélisateurs), sans accès à aucune expérience réelle de quoi que ce soit, qui n’ont jamais vu un malade de leur vie, et ce sont eux que le discours dominant (gouvernants, journalistes, "décideurs", etc.) crédite d’"expertise" et qui décident de votre réel à vous, à l’instar du célèbre Neil Ferguson, un charlatan maintenant bien connu, expert en statistiques et probabilités, la référence européenne en matière de modélisation des épidémies...

C’est ce même Neil Ferguson qui a fait parvenir le 12 mars dernier une note confidentielle à Emmanuel Macron prévoyant un demi-million de morts en France. Paniqué par cette perspective, le président français prit la décision d’un confinement généralisé le soir même...

On sait aussi que c’est ce même Neil Ferguson (devenu conseiller de la Banque mondiale et de nombreux gouvernements) qui, en 2001, avait convaincu le Premier ministre britannique Tony Blair de faire abattre 6 millions de bovins pour stopper l’épidémie de fièvre aphteuse (une décision qui coûta 10 milliards de livres et qui est aujourd’hui considérée comme aberrante). En 2002, l’expert Neil Ferguson calcula que la maladie de la vache folle tuerait environ 50 000 britanniques et 150 000 de plus lorsque elle se transmettrait aux moutons. Il y en eut en réalité 177. En 2005, il prédit que la grippe aviaire tuerait 65 000 Britanniques. Il y en eut au total 457.

C’est ce même genre de "raisonnement" qui fait conclure à l’Intelligence Artificielle qu’il faut une infirmière pour quinze lits, ou qu’un résident en Ehpad doit manger pour 4,57€ par jour. Ce qui se couvre aujourd’hui du nom de "science" est une idéologie d’élimination du sujet.

Ainsi au lieu de faire confiance à ceux qui ont à faire avec le réel de la chose (par exemple des vrais médecins agissant selon l’éthique médicale puisqu’en l’occurrence il s’agit de santé...), ce sont aux "grands débiles calculateurs" que font appel les gouvernements de nos sociétés du capitalisme numérique: ils cherchent des prédicateurs comme la Rome décadente consultait auspices et aruspices...

La prédiction est un art difficile, surtout lorsqu’il s’agit d’avenir.

Comme l'a noté Marx "L'anatomie de l'homme est la clé de l'anatomie du singe", l'histoire ne fait sens que rétroactivement, cette lecture, qui prend en compte la performativité rétroactive du signifiant, permet d'éviter le piège de la téléologie en faisant passer le sujet supposé croire (dans l’avenir) au sujet supposé savoir (du futur antérieur).

Ce "passage" permet d'entendre correctement la formule lacanienne (que Derrida n'a jamais comprise...)"une lettre arrive toujours à destination": qu’une lettre arrive toujours à destination, cela signifie que là où la lettre sera arrivée, cela aura été sa destination.

Primat absolu de la contingence (du Réel) sur la nécessité (Symbolique).

Voilà où réside la logique, et seul l’appareil logique démontre la faille du pur dire...

[wozziebear]

These and other surprising examples made it clear that mathematicians needed to prove that dimension is a real notion and that, for instance, n- and m-dimension Euclidean spaces are different in some fundamental way when n ≠ m. This objective became known as the “invariance of dimension” problem.

Finally, in 1912, almost half a century after Cantor’s discovery, and after many failed attempts to prove the invariance of dimension, L.E.J. Brouwer succeeded by employing some methods of his own creation. In essence, he proved that it is impossible to put a higher-dimensional object inside one of smaller dimension, or to place one of smaller dimension into one of larger dimension and fill the entire space, without breaking the object into many pieces, as Cantor did, or allowing it to intersect itself, as Peano did. Moreover, around this time Brouwer and others gave a variety of rigorous definitions, which, for example, could assign dimension inductively based on the fact that the boundaries of balls in n-dimensional space are (n − 1)-dimensional.

Although Brouwer’s work put the notion of dimension on strong mathematical footing, it did not help with our intuition regarding higher-dimensional spaces: Our familiarity with three-dimensional space too easily leads us astray. As Thomas Banchoff wrote, “All of us are slaves to the prejudices of our own dimension.”

Suppose, for instance, we place 2^n spheres of radius 1 inside an n-dimensional cube with side length 4, and then put another one in the center tangent to them all. As n grows, so does the size of the central sphere — it has a radius of √n − 1. Thus, shockingly, when n ≥ 10 this sphere protrudes beyond the sides of the cube.

The surprising realities of high-dimensional space cause problems in statistics and data analysis, known collectively as the “curse of dimensionality.” The number of sample points required for many statistical techniques goes up exponentially with the dimension. Also, as dimensions increase, points will cluster together less often. Thus, it’s often important to find ways to reduce the dimension of high-dimensional data.

The story of dimension didn’t end with Brouwer. Just a few years afterward, Felix Hausdorff developed a definition of dimension that — generations later — proved essential for modern math. An intuitive way to think about Hausdorff dimension is that if we scale, or magnify, a d-dimensional object uniformly by a factor of k, the size of the object increases by a factor of k^d. Suppose we scale a point, a line segment, a square and a cube by a factor of 3. The point does not change size (3^0 = 1), the segment becomes three times as large (3^1 = 3), the square becomes nine times as large (3^2 = 9) and the cube becomes 27 times as large (3^3 = 27).

One surprising consequence of Hausdorff’s definition is that objects could have non-integer dimensions. Decades later, this turned out to be just what Benoit B. Mandelbrot needed when he asked, “How long is the coast of Britain?” A coastline can be so jagged that it cannot be measured precisely with any ruler — the shorter the ruler, the larger and more precise the measurement. Mandelbrot argued that the Hausdorff dimension provides a way to quantify this jaggedness, and in 1975 he coined the term “fractal” to describe such infinitely complex shapes.

To understand what a non-integer dimension might look like, let’s consider the Koch curve, which is produced iteratively. We begin with a line segment. At each stage we remove the middle third of each segment and replace it with two segments equal in length to the removed segment. Repeat this procedure indefinitely to obtain the Koch curve. Study it closely, and you’ll see it contains four sections that are identical to the whole curve but are one-third the size. So if we scale this curve by a factor of 3, we obtain four copies of the original. This means its Hausdorff dimension, d, satisfies 3^d = 4. So, d = log3(4) ≈ 1.26. The curve isn’t entirely space-filling, like Peano’s, so it isn’t quite two-dimensional, but it is more than a single one-dimensional line.

A Mathematician's Guided Tour Through Higher Dimensions

https://www.quantamagazine.org/a-mathematicians-guided-tour-through-high-dimensions-20210913/ Comments

[1five1two]

Look at this world, full of wretched people, who imagine that they have possessions, worried that they might lose them and ever toiling in the hope of acquiring more. Look at all these people, striving after luxury and wealth, those whose riches are secured, whose stocks and shares are safely deposited, and who now nurture an insatiable appetite for knowledge, power, health, glory and pleasure.

Only he who recognizes that he has nothing, that he cannot possess anything, that security is unattainable, only he who completely resigns himself and sacrifices all, who gives everything, who does not know anything, who does not want anything and does not want to know anything, who abandons and neglects all, he will receive all. The world of freedom is opened to him, the world of painless contemplation and -- of nothing.

L.E.J. Brouwer

[ba3a-research-report]

Are Numbers Real?

https://books.google.co.uk/books?hl=en&lr=&id=C1r-9C8yP34C&oi=fnd&pg=PP1&dq=Mathematical+Thought+and+Its+Objects,+Cambridge:+Cambridge+University+Press&ots=YRwm0YhvTN&sig=voBJCal_MfS3K7rIv30iY9OAAQU#v=onepage&q=Mathematical%20Thought%20and%20Its%20Objects%2C%20Cambridge%3A%20Cambridge%20University%20Press&f=false

https://plato.stanford.edu/entries/philosophy-mathematics/

David Hilbert a mathematician from school of Formalism argues instead that,. “natural numbers can be taken to be symbols”. Symbols are undeniably abstract objects, however to be a symbol it must first be able to be embodied by a concrete object, therefore Hilbert argues that numbers can be considered “quasi-concrete objects”, having a tenuous link to the realm of “The Real”.

Mathematician and founder of the school of Intuitionism, L.E.J. Brouwer, states that “natural numbers are mental constructions, the real numbers are mental constructions, proofs and theorems are mental constructions, mathematical meaning is a mental construction [et. cetra]”, meaning that numbers exist entirely in the abstract, being formed solely in the mind, leading us to believe that numbers exist within the realm of “The Unreal”.

https://en.oxforddictionaries.com/definition/digital

https://www.philosophytalk.org/shows/what-are-numbers

https://welovephilosophy.com/2012/12/17/do-numbers-exist/

[logicmatters-blog]

Arend Heyting's proposed axioms to formalize the intuitionist programme of his teacher L.E.J. Brouwer.

[christian-dubuis-santini]

Idéologie, logique et psychanalyse

«…il faut quand même que je vous fasse sentir la portée d’une certaine façon dont moi je fraye la logique modale.

Le plus fort, hein, c’est que bien sûr, pour ce qui est de construire, pour ce qui est d’inventer…et voyez là tous les échos d’intuitionnisme qu’il vous plaira, si tant est que vous sachiez ce que c’est

…je vous ai traduit un jour le nécessaire par ce qui ne cesse pas de s’écrire.

Bon. Sachez-le, il y a une trace dans Aristote, que la logique propositionnelle… à savoir que quelque chose est vrai ou faux, ce qui se note 0 ou 1 selon les cas …il y a une petite trace, il y a un endroit où Aristote dérape - je vous montrerai ça quand vous voudrez - dans le Περὶ Ἑρμηνείας[Peri ermeneias] comme par hasard, De l’interprétation, pour ceux qui ne l’entravent pas –

il y a un endroit où ça fuse, que la logique propositionnelle est tout aussi modale que les autres.»

(Les non dupes errent)

Pour le psychanalyste, l’nconscient est ce qu’il y a de plus logique, l’écart ne passe pas entre le psychique et le somatique mais bien entre le psychique et le logique. Rien de plus logique qu’un psychotique...

Dans cet extrait des "non-dupes errent", Lacan lâche le mot d’"intuitionnisme"...

L'intuitionnisme (source Wiki) est une philosophie des mathématiques que L.E.J. Brouwer a élaborée au début du xxe siècle. Pour lui, les mathématiques sont une libre création de l'esprit humain et tous les objets qu'elles manipulent doivent être accessibles à l'intuition. L'intuitionnisme a pour conséquence une profonde remise en cause des mathématiques, notamment en refusant l'infini actuel: un nombre réel ne peut être représenté comme une suite infinie de décimales qu'à la condition de disposer d'un moyen effectif de calculer chacune de ces décimales; on parle alors de réel constructif.

Sur le plan logique, l'intuitionnisme n'accepte pas le raisonnement par l'absurde ou le tiers exclu pour la raison que ces principes permettent de démontrer des propriétés de façon non constructive: par exemple si on veut démontrer l'existence d'un nombre réel satisfaisant une certaine propriété, on peut raisonner par l'absurde, supposer qu'un tel réel n'existe pas, en déduire une contradiction et conclure que donc un tel réel existe, mais cette démonstration ne donne aucune indication sur la façon dont on pourrait calculer ce réel. Pour un intuitionniste on a juste démontré que l'existence d'un tel réel n'est pas contradictoire, mais pas que ce réel existe.

La logique intuitionniste a été développée par V. Glivenko et Arend Heyting, Kurt Gödel et Andreï Kolmogorov et formalise les principes logiques sur lesquels s'appuie l'intuitionnisme.

L'intuitionnisme est souvent considéré comme une forme de constructivisme, avec lequel il a beaucoup en commun, mais il s'en écarte quand, comme c'est le cas pour l'intuitionnisme originel de Brouwer, il conduit à des énoncés mathématiques valides qui ne le sont pas classiquement. La logique intuitionniste ne permet, elle, de démontrer que des énoncés valides en logique classique.

Voilà qui permet d’éclairer une partie des problèmes contemporains et notamment la colère de Didier Raoult contre le coup de force permanent des "méthodologistes" qui voudraient se faire passé pour "la Science" alors que la méthodologie n’est même pas une science.

Par exemple dans le pseudo-débat autour de la Chloroquine qui n’est en vérité que ’un enfumage idéologique ayant pour conséquence d’opposer deux types de rapport au langage et donc du sujet au réel, avec d’un côté:

– les partisans du médecin Didier Raoult qui avec son équipe a soigné directement cinq mille personnes infectées au coronavirus à Marseille, avec un taux de mortalité autour de 0,5%, et qui a fourni un suivi médical conséquent, avec toutes les études scientifiques afférentes, le docteur Raoult étant par ailleurs considéré comme l’un des plus grands infectiologues du monde, présentant un bilan réel, détaillé, argumenté dans les conditions réelles de maladie, de souffrance et de vie, et de l’autre côté:

– les tenants acharnés d’une version "Big Data", des geeks qui passent leur vie devant un ordinateur, dont les logiciels croisent des données (on les désigne aussi de l’acronyme MUM Mathématiciens Universitaires Modélisateurs), sans accès à aucune expérience réelle de quoi que ce soit, qui n’ont jamais vu un malade de leur vie, et ce sont eux que le discours dominant (gouvernants, journalistes, "décideurs", etc.) crédite d’"expertise" et qui décident de votre réel à vous, à l’instar du célèbre Neil Ferguson, un charlatan maintenant bien connu, expert en statistiques et probabilités, la référence européenne en matière de modélisation des épidémies...

C’est ce même Neil Ferguson qui a fait parvenir le 12 mars dernier une note confidentielle à Emmanuel Macron prévoyant un demi-million de morts en France. Paniqué par cette perspective, le président français prit la décision d’un confinement généralisé le soir même...

On sait aussi que c’est ce même Neil Ferguson (devenu conseiller de la Banque mondiale et de nombreux gouvernements) qui, en 2001, avait convaincu le Premier ministre britannique Tony Blair de faire abattre 6 millions de bovins pour stopper l’épidémie de fièvre aphteuse (une décision qui coûta 10 milliards de livres et qui est aujourd’hui considérée comme aberrante). En 2002, l’expert Neil Ferguson calcula que la maladie de la vache folle tuerait environ 50 000 britanniques et 150 000 de plus lorsque elle se transmettrait aux moutons. Il y en eut en réalité 177. En 2005, il prédit que la grippe aviaire tuerait 65 000 Britanniques. Il y en eut au total 457.

C’est ce même genre de "raisonnement" qui fait conclure à l’Intelligence Artificielle qu’il faut une infirmière pour quinze lits, ou qu’un résident en Ehpad doit manger pour 4,57€ par jour. Ce qui se couvre aujourd’hui du nom de "science" est une idéologie d’élimination du sujet.

Ainsi au lieu de faire confiance à ceux qui ont à faire avec le réel de la chose (par exemple des vrais médecins agissant selon l’éthique médicale puisqu’en l’occurrence il s’agit de santé...), ce sont aux "grands débiles calculateurs" que font appel les gouvernements de nos sociétés du capitalisme numérique: ils cherchent des prédicateurs comme la Rome décadente consultait auspices et aruspices...

La prédiction est un art difficile, surtout lorsqu’il s’agit d’avenir.

Comme l'a noté Marx "L'anatomie de l'homme est la clé de l'anatomie du singe", l'histoire ne fait sens que rétroactivement, cette lecture, qui prend en compte la performativité rétroactive du signifiant, permet d'éviter le piège de la téléologie en faisant passer le sujet supposé croire (dans l’avenir) au sujet supposé savoir (du futur antérieur).

Ce "passage" permet d'entendre correctement la formule lacanienne (que Derrida n'a jamais comprise...)"une lettre arrive toujours à destination": qu’une lettre arrive toujours à destination, cela signifie que là où la lettre sera arrivée, cela aura été sa destination.

Primat absolu de la contingence (du Réel) sur la nécessité (Symbolique).

Voilà où réside la logique, et seul l’appareil logique démontre la faille du pur dire...