#Class 12 Maths Vector Algebra

[dronacharyaiaschd]

Master 12th Math with the Best Tuition in Chandigarh

Master 12th Math with the Best Tuition in Chandigarh Mathematics in Class 12 is important in determining the academic life of a student. Whether you want to pursue engineering, commerce, or competitive exams, math literacy is crucial. The proper math tuition in Chandigarh can turn the tables and help you understand tricky concepts, enhance problem-solving ability, and increase confidence.

Why 12th Math Tuition in Chandigarh? Chandigarh boasts some of the top coaching centers offering professional guidance for Class 12 math preparation. Here's why professional tuition can be a game-changer: Personalized Learning Approach – Limited batch sizes allow students to receive personal attention, enabling them to clear doubts easily. Expert Faculty – Highly qualified teachers apply modern teaching methods to make difficult mathematical concepts easier. Regular Practice and Tests – Ongoing tests and assignments aid in monitoring progress and consolidating learning. Exam-Focused Preparation – A well-designed curriculum emphasizes crucial topics, past question papers, and competitive exam trends.

Major Topics Covered in 12th Math Tuition

A well-designed tuition course covers all the major Class 12 math topics as mandated by the CBSE and other boards. Some of the major areas are: Calculus – Differentiation, Integration, and Application of Derivatives Algebra – Matrices, Determinants, and Linear Programming Probability & Statistics – Conditional Probability, Mean, Median, and Standard Deviation Coordinate Geometry – Three-Dimensional Geometry and Vectors Relations & Functions – Inverse Trigonometric Functions and Continuity

How to Select the Best Math Tuition in Chandigarh?

Getting the most appropriate tuition center is a thoughtful decision based on numerous factors: Faculty Experience – Inspect the education and experience of teachers. Student Reviews and Success Rate – Check previous outcomes and students' reviews. Flexible Batch Timings – Make sure the class timing is compatible with your study schedule. Doubt-Solving Sessions – Provision of additional classes for resolving doubts.

Conclusion Excelling in Class 12 mathematics requires the right guidance, consistent practice, and strategic preparation. Enrolling in the best math tuition in Chandigarh can help you build a strong foundation and secure excellent marks in your board exams. With expert coaching, a structured curriculum, and personalized attention, you can overcome challenges and master every concept with ease. Start your journey today and make math your strength!

[shiva10010]

JEE Main 2025! Prep Your Math Strategy with the Latest Syllabus

The Joint Entrance Examination (JEE) Main is a critical gateway for aspiring engineers in India. While the official syllabus for JEE Main 2025 will likely be released by the National Testing Agency (NTA) in November 2024, you can get a head start on your preparation using the previous year's syllabus as a guide.

This article focuses on the Mathematics section of the JEE Main 2025 exam.

Key Elements of the JEE Main 2025 Maths Syllabus

The JEE Main Maths syllabus covers a wide range of topics from Class 11 and 12 NCERT textbooks. Here's a quick glimpse of the major areas you'll encounter:

Algebra: Sets, relations and functions, complex numbers, matrices and determinants, mathematical induction, binomial theorem, sequence and series.

Calculus: Limit, continuity and differentiability, integral calculus, differential equations.

Geometry: Coordinate geometry, three-dimensional geometry, vector algebra.

Other Quantitative Techniques: Statistics and probability, trigonometry, mathematical reasoning.

Why eSaral is Your Perfect JEE Main 2025 Maths Companion

While the syllabus provides a roadmap, in-depth preparation is essential for success. This is where eSaral steps in:

Complete Syllabus Coverage: eSaral ensures you cover all the essential JEE Main Maths topics.

Detailed Learning Material: Access a treasure trove of resources, including crisp explanations, illustrative examples, and topic-wise revision notes [refer to JEE Main 2025 Maths Revision Notes on eSaral for details].

Catered Learning Styles: Whether you prefer short and focused content or a deep dive into concepts, eSaral offers options to match your learning style.

Practice Makes Perfect: Sharpen your skills with ample practice problems available on the platform.

Additional Tips to Conquer JEE Main 2025 Maths

Focus on NCERT Textbooks: They form the foundation for the entire syllabus.

Regular Practice: Solve problems consistently to build speed, accuracy, and exam temperament.

Mock Tests: Take regular mock tests to simulate the exam environment and identify areas for improvement.

Clear Your Doubts: Don't hesitate to seek clarification from teachers or online forums.

Conclusion

JEE Main 2025 Maths can be aced with the right approach and resources. By leveraging the detailed syllabus and comprehensive learning materials offered by eSaral, you can approach the exam with confidence and a strategic plan. Remember, consistent effort and focused practice are key to achieving your engineering dreams.

[mpboardsolutions-blog]

MP Board Class 12th Maths Book Solutions in English Medium

MP Board Class 12th Maths Chapter 1 Relations and Functions

Chapter 1 Relations and Functions Ex 1.1

Chapter 1 Relations and Functions Ex 1.2

Chapter 1 Relations and Functions Ex 1.3

Chapter 1 Relations and Functions Ex 1.4

Chapter 1 Relations and Functions Miscellaneous Exercise

MP Board Class 12th Maths Chapter 2 Inverse Trigonometric Functions

Chapter 2 Inverse Trigonometric Functions Ex 2.1

Chapter 2 Inverse Trigonometric Functions Ex 2.2

Chapter 2 Inverse Trigonometric Functions Miscellaneous Exercise

MP Board Class 12th Maths Chapter 3 Matrices

Chapter 3 Matrices Ex 3.1

Chapter 3 Matrices Ex 3.2

Chapter 3 Matrices Ex 3.3

Chapter 3 Matrices Ex 3.4

Chapter 3 Matrices Miscellaneous Exercise

MP Board Class 12th Maths Chapter 4 Determinants

Chapter 4 Determinants Ex 4.1

Chapter 4 Determinants Ex 4.2

Chapter 4 Determinants Ex 4.3

Chapter 4 Determinants Ex 4.4

Chapter 4 Determinants Ex 4.5

Chapter 4 Determinants Ex 4.6

Chapter 4 Determinants Miscellaneous Exercise

MP Board Class 12th Maths Chapter 5 Continuity and Differentiability

Chapter 5 Continuity and Differentiability Ex 5.1

Chapter 5 Continuity and Differentiability Ex 5.2

Chapter 5 Continuity and Differentiability Ex 5.3

Chapter 5 Continuity and Differentiability Ex 5.4

Chapter 5 Continuity and Differentiability Ex 5.5

Chapter 5 Continuity and Differentiability Ex 5.6

Chapter 5 Continuity and Differentiability Ex 5.7

Chapter 5 Continuity and Differentiability Ex 5.8

Chapter 5 Continuity and Differentiability Miscellaneous Exercise

MP Board Class 12th Maths Chapter 6 Application of Derivatives

Chapter 6 Application of Derivatives Ex 6.1

Chapter 6 Application of Derivatives Ex 6.2

Chapter 6 Application of Derivatives Ex 6.3

Chapter 6 Application of Derivatives Ex 6.4

Chapter 6 Application of Derivatives Ex 6.5

Chapter 6 Application of Derivatives Miscellaneous Exercise

MP Board Class 12th Maths Chapter 7 Integrals

Chapter 7 Integrals Ex 7.1

Chapter 7 Integrals Ex 7.2

Chapter 7 Integrals Ex 7.3

Chapter 7 Integrals Ex 7.4

Chapter 7 Integrals Ex 7.5

Chapter 7 Integrals Ex 7.6

Chapter 7 Integrals Ex 7.7

Chapter 7 Integrals Ex 7.8

Chapter 7 Integrals Ex 7.9

Chapter 7 Integrals Ex 7.10

Chapter 7 Integrals Ex 7.11

Chapter 7 Integrals Miscellaneous Exercise

MP Board Class 12th Maths Chapter 8 Application of Integrals

Chapter 8 Application of Integrals Ex 8.1

Chapter 8 Application of Integrals Ex 8.2

Chapter 8 Application of Integrals Miscellaneous Exercise

MP Board Class 12th Maths Chapter 9 Differential Equations

Chapter 9 Differential Equations Ex 9.1

Chapter 9 Differential Equations Ex 9.2

Chapter 9 Differential Equations Ex 9.3

Chapter 9 Differential Equations Ex 9.4

Chapter 9 Differential Equations Ex 9.5

Chapter 9 Differential Equations Ex 9.6

Chapter 9 Differential Equations Miscellaneous Exercise

MP Board Class 12th Maths Chapter 10 Vector Algebra

Chapter 10 Vector Algebra Ex 10.1

Chapter 10 Vector Algebra Ex 10.2

Chapter 10 Vector Algebra Ex 10.3

Chapter 10 Vector Algebra Ex 10.4

Chapter 10 Vector Algebra Miscellaneous Exercise

MP Board Class 12th Maths Chapter 11 Three Dimensional Geometry

Chapter 11 Three Dimensional Geometry Ex 11.1

Chapter 11 Three Dimensional Geometry Ex 11.2

Chapter 11 Three Dimensional Geometry Ex 11.3

Chapter 11 Three Dimensional Geometry Miscellaneous Exercise

MP Board Class 12th Maths Chapter 12 Linear Programming

Chapter 12 Linear Programming Ex 12.1

Chapter 12 Linear Programming Ex 12.2

Chapter 12 Linear Programming Miscellaneous Exercise

MP Board Class 12th Maths Chapter 13 Probability

Chapter 13 Probability Ex 13.1

Chapter 13 Probability Ex 13.2

Chapter 13 Probability Ex 13.3

Chapter 13 Probability Ex 13.4

Chapter 13 Probability Ex 13.5

Chapter 13 Probability Miscellaneous Exercise

[ncertmcq]

Vector Algebra Class 12 Notes Maths Chapter 10

[meritbatch]

NCERT Solutions for Class 12 Maths Chapter 10 Vector Algebra

[efastforward123]

E Fast Forward

JEE Main Syllabus: Physics, Chemistry and Maths

JEE Main is one of the most prestigious engineering entrance exams in India. The JEE Main exam serves as a gateway for admission to the top engineering colleges in India, including the Indian Institutes of Technology (IITs) and the National Institutes of Technology (NITs). The exam is conducted by the National Testing Agency (NTA) twice a year, and the syllabus for JEE Main is vast and includes topics from class 11 and 12.

Mathematics

Trigonometry is an integral part of JEE Main maths and includes various subtopics such as trigonometric ratios, trigonometric identities, and trigonometric equations. Coordinate geometry involves understanding the relationship between geometrical figures and the coordinate plane. Vectors are utilized to describe the direction and magnitude of a particle. Understanding the concepts of all these topics is crucial to score well in the JEE Main maths section. One of the most common mistakes students tend to commit in the JEE Main maths section is that they tend to waste a lot of time on simple questions. To avoid this, students should strategically plan their exam and focus on solving the difficult questions first.

Physics

Optics is another crucial topic in JEE Main physics and involves the study of light and its behavior. Students need to have a good understanding of concepts such as reflection, refraction, lenses, and mirrors. Modern physics is also an essential topic in JEE Main and includes subtopics such as wave-particle duality, photoelectric effect, and nuclear physics.

Chemistry

Chemistry requires a lot of practice, and it is recommended to attempt as many questions from previous year’s papers as possible. One way to prepare for JEE Main chemistry is to focus on practicing chemical reactions and reaction mechanisms. Students must have a thorough understanding of the periodic table and chemical bonding to score well in JEE Main chemistry.

Exam Pattern and Marking Scheme

The JEE Main exam is conducted both online and offline and consists of three sections, including physics, chemistry, and mathematics. The physics and chemistry sections consist of 30 questions each, while the maths section consists of 25 questions. The JEE Main exam is for a total of 360 marks, and each question carries four marks. However, for every wrong answer, one mark is deducted, and for any unanswered question, no marks are deducted.

It is essential to read the question paper carefully and plan the exam strategy accordingly. It is always advisable to attempt the questions in which students are confident, and they must avoid negative marking.

NCERT Books

NCERT books are an essential part of JEE Main preparation. More than 60% of the JEE Main syllabus is covered in NCERT books. NCERT books are beneficial in providing a strong foundation for students by developing their concepts from the basics. Students should start with NCERT books before moving on to other reference books.

Students must focus on the key topics of NCERT books, which are crucial for JEE Main. These topics include calculus, algebra, mechanics, optics, and chemical reactions. Students should read the NCERT books carefully, focus on important sections, and take notes for future revisions.

Online Resources and Mock Tests

There are many online resources that students can use to prepare for JEE Main. Students can access online sample papers, previous year’s JEE Main question papers, and tutorials to help them prepare for the exam. There are many websites and apps that provide video lectures, practice questions and solutions for JEE Main.

Download Android App

Mock tests are important for JEE Main preparation as they help in identifying the strengths and weaknesses of students. By taking mock tests, students can gauge their level of preparation and get a feel for the actual exam. Many websites provide free mock tests that mimic the JEE Main exam pattern, which students should take to improve their scores.

Time Management for JEE Main

During the exam, students should allocate their time wisely and attempt only those questions they are confident about. They should avoid getting stuck on a particular question and move forward if they are unable to solve it. Students must keep track of time during the exam and must allocate sufficient time for revising their answers.

Revision Techniques

Revision is important for JEE Main as it helps in consolidating knowledge and improves memory retention. Revision techniques such as active recall, spaced repetition, and mind maps can help students in retaining information more effectively.

Students should create revision notes while studying for JEE Main and revise them regularly. They should focus on understanding the concepts and not just memorizing them. They can use flashcards to revise key concepts or formulas, which will help them in retaining the information for longer.

JEE Main is a challenging exam, and it requires dedication, focus, and hard work. To score well in JEE Main, students must have a clear understanding of the syllabus and develop a sound strategy for preparing for the exam. Students must focus on the essential topics, practice regularly, and take mock tests to enhance their chances of success. Effective time management, revision, and online resources can help students in achieving their goal of cracking JEE Main.

[vectoralgebraclass12]

Vector Algebra is a one of the basic topics that is necessary to understand the various concepts of Physics and Mathematics. Vector Algebra is the prerequisite for concepts like Kinematics and basics for students intended to go for engineering studies like IIT JEE Mains, other entrances, boards, and higher studies in Mathematics. It covers all the basic to advance concepts, each NCERT Solutions, R.D Sharma, R.S Aggarwal, Board’s Question Bank, Important Examples and Comprehensive Educational Resources for Vector Algebra Class 12 Maths including Assignments and high-quality video lectures prepared by expert teacher from the boards point of view.

Vector Algebra Class 12 Maths

[quietimtryingtostudy]

me looking at my math notebook blurry eyed: 

i sit by myself talking in my roooomm tryna understand youuuu

[ashishkumarletslearn]

Vector Algebra Class 12 Maths IIT JEE Mains

Detailed explanation of vectors and scalars, magnitude and direction of a vector.Direction cosines and direction ratios of a vector. Types of vectors (equal, unit, zero, parallel and collinear vectors), position vector of a point, negative of a vector, components of a vector, addition of vectors, multiplication of a vector by a scalar, position vector of a point dividing a line segment in a given ratio. Definition, Geometrical Interpretation, properties and application of scalar (dot) product of vectors, vector (cross) product of vectors including basics to advance level concepts, NCERT Solutions, R.D Sharma, R.S Aggarwal, Important Examples from the boards point of view for NCERT Chapter 10 Vector Algebra Class 12 Maths IIT JEE Mains.

Below is the list of High-Quality Video Lectures links for Vector Algebra Class 12 Maths:

Lecture -1 Vector Algebra Class 12 Maths Chapter 10

NCERT Exercise 10.1 Vector Algebra Class 12 Maths

NCERT Exercise 10.2 Vector Algebra Class 12 Maths

How to study Vector Algebra & Three Dimensional Geometry?

[cbse-board]

Detailed explanation of ‘how to represent vectors, types of vectors and ncert solutions for Exercise 10.1 of Chapter 10 Vector Algebra Class 12 Maths.

#VectorAlgebra #Class12Maths

[penguin-ghost]

Week 0 - What I am taking this semester

Uni starts next Monday!

As a Physics and Philosophy major, I’ve enrolled in 5 units of study this semester:

Physics 1A

This is introductory physics course, and I'm taking the advanced stream that will be more fast paced. We will cover 3 modules this semester:

Mechanics

Thermal Physics

Oscillations, Chaos and Waves

Physics is my main interest, and although the introductory class doesn’t have very exciting modern physics, I’m still pretty hyped about learning Physics at a more advanced level with a lot of maths.

Reality, Ethics and Beauty

This is an introductory philosophy class that discusses the central issues in metaphysics, ethics and aesthetics. We will begin with the philosophy of religion, and the reading for Week 1 is on Thomas Aquinas and his five ways. I've never formally studied philosophy, so I am also super hyped about this class too.

Linear Algebra

I think I'm excited for every class hahaha. We are required to watch pre-lecture videos (produced by the professor) to familiarise ourselves with the material, so that harder content and examples can be covered in the actual lectures. I genuinely enjoy this learning format, and I think it's effective for me. I've already watched and made notes on the first set of videos on Vectors in R^n and Vector Space. It doesn't take long to realise that uni maths is a lot more reliant on symbols rather than words, so I will have to get used to reading and interpreting them faster.

Calculus of One Variable

We will begin with complex numbers! This was my favourite maths topic back in Year 12. But I'm not sure how much of a revision it'll be - it's been more than 100 days since I've last touched any maths, let alone maths on the complex plane. And by the look of the unit schedule, the pace for the class is really fast. A little worried.

Introduction to Programming

I have attempted to learn how to code on at least 3 occasions. Never succeeded. It's got to a point where I don't even know what my attitude towards programming is anymore. Who knows, maybe it’ll be fun. It's also quite essential for my physics career so I will try to enjoy it as much as I can.

p.s. All of my classes are remote, as I am currently away from Campus, and I will be doing weekly updates on how I find uni.

[valpy-blog]

NCERT Solutions for Class 12 Maths Chapter 10 Vector Algebra Ex 10.4

NCERT Solutions for Class 12 Maths Chapter 10 Vector Algebra Ex 10.4

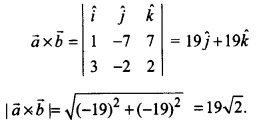
NCERT Solutions for Class 12th Maths Chapter 10 Vector Algebra Ex 10.4

Get Free NCERT Solutions for Class 12 Maths Chapter 10 Vector Algebra Ex 10.4 PDF in Hindi and English Medium. Sets Class 12 Maths NCERT Solutions are extremely helpful while doing your homework. Vector Algebra Exercise 10.4 Class 12 Maths NCERT Solutions were prepared by Experienced LearnCBSE.in Teachers. Detailed answers of…

[anushacbse]

CBSE Class 12 Maths Revision Notes

Class 12 Maths Notes: Class 12 Maths Notes is designed to help for the students who are going to appear final exams, students can read this CBSE Class 12 Maths Revision Notes before going to exam to cover all chapters and topics in last minute and can easily revise all chapters of class 12 Maths. Important topics like Trigonometry, integrals, equations and three-dimensional geometry has been included in Class 12 Maths Notes. For CBSE Students board exams will be conducted by NCERT. Class 12 Maths Notes has been designed on the basis of the latest NCERT syllabus textbooks. So students can check CBSE Class 12 Maths Quick Revision Notes and can download the solutions in PDF’s format as well. Students can practice the Class 12 Maths Revision Notes to gain more knowledge.

Class 12 Maths consists of 13 Chapter below is the list of chapter Names.

Chapter 1: Relations and Functions Chapter 2: Inverse Trigonometric Functions Chapter 3: Matrices Chapter 4: Determinants Chapter 5: Continuity and Differentiability Chapter 6: Application of Derivatives Chapter 7; Integrals Chapter 8: Application of Integrals Chapter 9: Differential Equations Chapter 10: Vector Algebra Chapter 11: Three Dimensional Geometry Chapter 12: Linear Programming Chapter 13: Probability

Students can download the PDF’s of Class 12 Maths Revision Notes. The Class 12 Maths Notes will also help in understanding the chapters properly as it will contain the important points for revision purpose in short times