#3d cellular automaton

[msexcelfractal]

5x5 Diamond rule, iterates 1-32

Iterates 40, 48, 56

Iterate 64

Iterate 128

This is a 2D cellular automaton generating a 3D fractal layer by layer. I coded it in Microsoft Excel - each pixel is 1 cell.

See more MSExcel fractals

[songrolli]

3d cellular automaton

3d cellular automaton full#

An alternative class of models which take into account the distribution of toughness is cellular automata finite element models (CAFE). This is because there is no information on the microstructure such as grain size and morphology, texture, and other important features considered in them. While the probabilistic approaches provide a sound scientific basis for capturing the scatter in the fracture data through assuming a probability for the presence of fracture initiators, their microstructurally agnostic assumptions can limit their predictive capability. More suitable probabilistic methods have been devised to describe the scatter associated with fracture.

3d cellular automaton full#

Therefore, deterministic approaches do not give full picture of scatter in fracture behaviour. This is evidenced by scatter in the toughness of seemingly identical specimens. The relative error of grain size before and after heat preservation is in the range of 0.1–0.6 μm, which indicates that the 3D cellular automata can accurately simulate the heat preservation process of AZ31 magnesium alloy.įracture is an inherently statistical phenomenon as it is a function of micro-structural heterogeneities such as distributed defects and inclusions. The angle between the two-dimensional slices of three-dimensional grains is approximately 120°, which is consistent with that of the traditional two-dimensional cellular automata. The grain of AZ31 magnesium alloy increases in size with the increase of temperature, and the number of grains decreases with the increase in time. Grains of different sizes are distributed normally at different times, most of which are grains with the ratio of grain diameter to average grain diameter R/Rm ≈ 1.0, which meets the minimum energy criterion of grain evolution. The results show that the normal growth of three-dimensional grains satisfies the Aboav-weaire equation, the average number of grain planes is between 12 and 14 at 420☌ and 2000 CAS, and the maximum number of grain planes is more than 40. Also, the effect of temperature on the three-dimensional grain growth process of AZ31 magnesium alloy is analyzed. However, further coarray optimi-sation is needed to narrow the performance gap between coarrays and MPI.īased on the thermodynamic conversion mechanism and energy transition principle, a three-dimensional cellular automata model of grain growth is established from the aspects of grain orientation, grain size distribution, grain growth kinetics, and grain topology. Overall, the results look promising for coarray use beyond 100k cores. The sampling and tracing analysis shows good load balancing in compute in all miniapps, but imbalance in communication, indicating that the difference in performance between MPI and coarrays is likely due to parallel libraries (MPICH2 vs libpgas) and the Cray hardware specific libraries (uGNI vs DMAPP). This is further evi-denced by the fact that very aggressive cache and inter-procedural optimisations lead to no performance gain. This is likely because the CA algorithm is network bound at scale. Adding OpenMP to MPI or to coarrays resulted in worse L2 cache hit ratio, and lower performance in all cases, even though the NUMA effects were ruled out. MPI halo exchange (HX) scaled better than coarray HX, which is surprising because both algorithms use pair-wise communications: MPI IRECV/ISEND/WAITALL vs Fortran sync images. Ping-pong latency and bandwidth results are very similar with MPI and with coarrays for message sizes from 1B to several MB. The work was done on ARCHER (Cray XC30) up to the full machine capacity: 109,056 cores. Ising energy and magnetisation were calculated with MPI_ALLREDUCE and Fortran 2018 co_sum collectives. Scaling of coarrays is compared in this work to MPI, using cellular automata (CA) 3D Ising magnetisation miniapps, built with the CASUP CA library,, developed by the authors. Fortran coarrays are an attractive alternative to MPI due to a familiar Fortran syntax, single sided communications and implementation in the compiler.

[mobiletaggingart]

Blockchain. Cellular Automata A cellular automaton is a collection of cells on a grid with specific shapes that evolve through a number of steps from a set of rules based on the states of neighboring cells.

[christophwagner]

Having Fun with Proccesing.js: Langton’s Ant

The other day I solved an interesting problem on CodeWars, called Langton’s Ant. It’s a type of cellular automaton that runs on a 2-dimensional infinite grid and moves according to two very simple rules:

If the current field is colored white, make it black, turn 90 degrees to the right, and move one step forward.

If the current field is colored black, make it white, turn 90 degrees to the left, and move one step forward.

While the CodeWars problem only required you to compute a few iterations of the ant’s movement and return the resulting state of the grid, I thought it would be interesting to make a visual version that runs in the browser.

After a bit of research, I finally settled on Processing.js. Initially I had avoided it, because I did not want to learn yet another language, but after wasting a whole day trying to do pixel graphics with the Canvas API, I figured I might as well give it a shot.

Turns out it’s a near perfect fit for this exercise, and not just because it provides a point primitive, which the Canvas API does not. Processing is a very simple, C-like language that is optimized for 2D graphics. The basic program structure is extremely simple: there is a setup() function and a draw() function. The former is called once at the start of your program, while the latter is called repeatedly in order to update the screen.

But enough of the theory, let’s see the result:

JS Bin on jsbin.com

The interesting thing about Langton’s Ant is that despite its incredibly simple rules, it produces some rather interesting behavior. For a few minutes, it seems to run around the center aimlessly, until suddenly, it starts creating a sort of “highway” leading to the lower right hand corner.

If you leave it running long enough, it will eventually hit the edge of the screen and stop there, because I didn’t implement any overflow behavior, so the code will just crash at this point. One way to solve this would perhaps be by shifting the offset of the grid in the canvas, or scaling down the size of the pixels. I might try implementing that next time.

UPDATE: The new version now automatically scales the resolution once the ant hits the borders of the screen. However, once the ant starts building its highway, it will inevitably run out of space eventually. 

The other interesting thing, from a computer science perspective, is the fact that the Ant works like a 2-dimensional Turing Machine. That means that given the right input (i.e. a pre-populated grid), it can compute the solution to any algorithmic problem (if given enough time).

Another idea I’d like to pursue in the future is generalizing the ant to 3 dimensions, by giving it the ability to rotate around all 3 axes (and yes, that is indeed the correct plural form of “axis”). This would mean I’d have to introduce more colors (two per axis). I’m curious to see if that same emergent behavior also works in 3D.

[saunthinks]

Trying to Articulate My Project 

Hello Everyone!

The project begun because I feel alienated from my work when I check my emails or explore the web. My computer knows me intimately, but I can’t begin to understand its complex interconnected order of operations. Its inner workings are mystified in the name of sleek design and oversimplification for understanding’s sake. Truthfully, I am not meant to know. The technicalities that often exclude and work against me are kept secret.

The virtuality of computing, and the cyberspace often gloss over its material reality (satellites, mainframes, fans) through its depictions of clouds or green text in a black void, painted as a magical entity. I feel the need to materialise them through crafts, a medium I feel close with due to its tactility, to demystify them.

In my context report, I traced the thread between craft and computing through its history with women’s work. Women Weaving the Web. I focus on the increasingly influential algorithm, often unjust (sexist, racist) in its biased training data sets. I wish to visualise/materialise/expose an algorithm’s degree of power as it dictates more of our futures; in transportation, recruiting, finance and more..

Before the lockdown I was experimenting with the 3d-potter and when the labs shut, I weaved. First I weaved a logic if function I did on Excel, then I started playing with computer hardware as material for weaving. I’ve been getting into the cellular automaton as well as genetic algorithms, both having potentials of being very visual. (Maybe I should be looking at more algorithms??) I thought that I could hopefully make an algorithm that would create an evolving pattern which I could feed into a computerised loom (like the TC2 loom), but the design dept doesn’t have any looms. Then again, it doesn’t have to be a weaving..

So.. this is where I’m at :’/ I spent today putting off actually articulating all these thoughts and pondering how I actually wanted my object to exist in the world (hence the very late email, sorry). I think I would like it to be a physical materialisation of my relationship with computing through craft, that would connect back into the virtual and continue on????

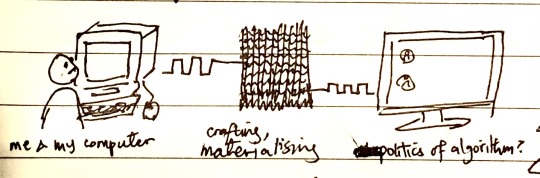
Hopefully, this isn’t too much of a long-winded mess, thank you so so much for the help! I’m missing seeing everyone around the labs very much </3 But I am looking forward to the meeting tomorrow. (or is it today now that its 4am?)

Bestest,

Saundra

[wolframalpha]

Stephen Wolfram’s Twitch Streams

ICYMI, Stephen Wolfram has been busy on Twitch! Here are his streams from June, some taking place at the Wolfram Summer School & Camp.

Introducing a New Kind of Coding

Cellular Automata & Deep Learning

A Data Curation Adventure

Searching for a 3D Cellular Automaton

[msexcelfractal]

What I'm up to: a programmable 3D cellular automaton fractal generator in Excel. My prior work has been with the 2D output of a 1D cellular automaton that runs line-by line (or diagonally) in Excel. EG a 1-array of cells in a row scan the previous row(s) using modular arithmetic to decide their own states. As row after row fills, a fractal emerges.

Now I am making the 1D array into a 2D array. The downside is low resolution: I have to allocate a plane square with hard-coded maximum dimensions for each subsequent iteration to render smoothly in its own area. Instead of generating one 400x400 or 800x800 output from a spreadsheet I'm generating a long series of 64x64 or 81x81 outputs.

The upsides are two-fold:

The 3D patterns are much less likely to "chaos out". Rules are more likely to resolve into recognizable figures that are pleasing to the eye.

40 stages each of an octahedral rule mod 6 and a Menger variant mod 3.

The stages of 3D construction often reveal secrets about how the 2D fractals I've collected are formed (in terms of their symmetry formats as well as their relationships to each other.)

Some insight into the construction of "headache"

[shogonu]

2D and 3D cellular automaton of VR for HTC Vive. DVERSE Inc. logo is designed in the motif of a "glider" of Conway's game of life:) Free DL http://s3.dverse.me/engineerblog/GameOfLifeVR01a.zip #dverse #symmetryvr #vr #oculusrift #htcvive #virtualreality #gameoflife

[mobiletaggingart]

  Serie Autómata Celular 3D-fractal, 3D-print, PLA plastic 10″×10″. 2017. Digital art

PEDRO MORALES

Un autómata celular es una colección de celdas “coloreadas” en una cuadrícula con formas especificas que evoluciona a través de un número de pasos a partir de un conjunto de reglas basadas en los estados de las celdas vecinas.

Un autómata celular (AC) es una matriz, donde las celdas cambian o no de estado, tomando por ejemplo valores de cero o uno, a cada golpe de reloj. El nuevo valor obedece a leyes simples que evalúan los estados de las células vecinas. Si se logran las configuraciones y las leyes adecuadas, pueden obtenerse objetos rebosantes de complejidad y belleza.

El Sagrado Corazón Serie Autómata Celular 3D-fractal, 3D-print, PLA plastic 10″×10″. 2017. Digital art PEDRO MORALES Un autómata celular es una colección de celdas "coloreadas" en una cuadrícula con formas especificas que evoluciona a través de un número de pasos a partir de un conjunto de reglas basadas en los estados de las celdas vecinas.

[rsshonjoy]

OnePlus 7 Pro Dual Sim Factory Unlocked GM1917 12GB+256GB Nebula Blue (ATT, Verizon, Tmobile) - US Warranty Price:880.46$ Buy Now: Click Here! OnePlus seven professional, America Version model GM1917 with America warrant, operative System: OxygenOS supported automaton nine (Pie), CPU: Qualcomm flower 855 (Octa-core, 7nm processor), 12GB Memory 256GB Storage, In-Display Fingerprint device, twin SIM – This plant unfastened phone is compatible worldwide. In America it’s compatible with carriers like Verizon, AT&T, T-Mobile, H20, easy Mobile, shopper Cellular, Metro PCS, Cricket, Straight speak GSM, Tracfone GSM, Ting GSM, Project Fi GSM and different postpaid carriers. Display Size: vi.67 inches QHD+ AMOLED show | Resolution: 1440 x 3120 pixels, side Ratio: nineteen.5:9 | Type: AMOLED | cowl Glass: 3D Corning Gorilla gorilla Glass. 90Hz Refresh Rate: delivers a fluid viewing expertise that produces everything you are doing quicker and sander. HDR 10+. In-display fingerprint device - merely bit the screen to unlock your device in mere zero.21 seconds. Triple Rear Camera: 48MP Main (f/1.6) + 16MP immoderate Wide Angle (f/2.2) + 8MP pic (f/2.4). twin diode Flash, Video: 4K resolution at 30/60 Federal Protective Service | 1080p resolution at 30/60 Federal Protective Service | Super Slow Motion: 1080p videos at 240 Federal Protective Service | 720p video at 480 Federal Protective Service, Time-Lapse, Video Editor. Pop-up front camera: 16MP, Video: 1080p resolution at thirty Federal Protective Service | Time-Lapse. FDD LTE: Band B1/2/3/4/5/7/8/12/13/17/18/19/20/25/26/28/29/30/66/71, TDD-LTE: Band B34/38/39/41/46/48, UMTS(WCDMA): Band B1/2/4/5/8/9/19, CDMA: BC0/BC1, GSM: 850/900/1800/1900 Mc. In the box: 1x OnePlus seven professional | 1x Screen shielder (pre-applied) | 1x Case | 1x OnePlus quick Charge Type-C Cable | 1x OnePlus quick Charge Power Adapter (US Charger) | 1x SIM receptacle Ejector | 1x fast begin Guide | 1x Safety data | 1x Type-C to three.5 millimetre phone Jack Adapter

http://onlineshoppingrs5.blogspot.com/2019/10/oneplus-7-pro-dual-sim-factory-unlocked.html

[lunaeclipse-world]

Francis Bitonti creates pixellated 3D-printed shoes using cellular automaton…. Francis Bitonti creates pixellated 3D-printed shoes using cellular automaton. Source by ioannidouv

[matteorossini]

This color-shifting lizard's skin morphs just as Alan Turing predicted

There’s a particular type of lizard that changes the color of its spots as it ages — and researchers have just discovered the mathematical rules that govern this peculiar metamorphosis.

Meet the ocellated lizard, a 30-to-35 inch reptile that lives Europe. These lizards are born with unimpressive brown and white polka dots. But as they grow, they develop this beautiful, labyrinthine green and black pattern across their bodies. We don’t know exactly why this happens, but now, we know a little more about how. The lizard scales might be changing according to a particular mathematical model, reports a study published this week in Nature. The weird thing is, this model is somewhat different from the one that scientists have long believed to determine how animals get dots and stripes.

In fact, one overarching theory of how biological patterns form comes from an unlikely place: codebreaker Alan Turing. About 65 years ago, he proposed that stripes, spots, and even appendages like fingers may emerge from a series of chemical interactions between two hypothetical substances: an activator and an inhibitor. As both substances spread across a canvas like an animal’s skin at different paces, they compete with one another to give rise to patterns.

Watch this MinuteEarth video for an explanation of Turing’s model:

Scientists are still figuring out which specific dots ands stripes develop from a Turing mechanism, and what the actual activators and inhibitors are in living creatures. But evolutionary biologist Michel Milinkovitch wanted to see if Turing’s model also apply to how ocellated lizards change the color of its scales..

Milinkovitch’s lab is interested in beauty and the rules that control it, he says. So he and his colleagues took 3D scans of three ocellated lizards over three years, starting when they first hatched, to track how their colors changed over the years. They discovered something peculiar: the scales continued to flip from green to black, or black to green, depending on the color of their neighbors. Generally the green scales were surrounded by four black and two green scales, while the black scales were surrounded by three black and three green scales. (The researchers ignored the lizard’s belly scales and the blue spots for this analysis.)

That reminded Milinkovitch of a mathematical model developed by John von Neumann in the 1940s, called a cellular automaton. This computing model is basically a grid of connected units, and the state of each unit is governed by the state of its neighbors. (This is fairly easy to understand if you play with a simulation, and sort of difficult to explain with words, so click this link to play with the most famous cellular automaton ever, Conway’s The Game of Life.) Milinkovitch wondered if this mathematical model could be showing up in a living creature: “What if each scale is changing color as a function of the state of its neighbor?”

This animated cellular automaton is a variation of the Game of Life called the Glider Gun.

Created by Johan G. Bonte using Life32 v2.15 beta, via Wikimedia Commons.

When he and his colleagues crunched the numbers, he turned out to be right. “Each scale senses the color of its neighbors and then takes a decision on the basis of its neighborhood,” he says. Milinkovitch is still narrowing down exactly what biological signals govern this.

But it’s not that the Turing mechanism gets completely lost. In fact, when Milinkovitch and his colleagues tweaked their model to incorporate the thickness of the scales, and the thinness of the skin between them, suddenly Turing’s model worked: basically, with the right parameters, Turing’s model could create von Neumann’s cellular automaton — on a living creature’s skin.

This study reveals that “a cellular automaton is not just an abstract concept, but corresponds to a process generated by biological evolution,” Leah Edelstein-Keshet, a mathematician at the University of British Columbia, writes in a commentary published alongside Milinkovitch’s paper. So, why does that matter? “We just want to understand better the universe,” Milinkovitch says. “And in this case, our universe is this beautiful lizard.”

from The Verge http://ift.tt/2p89fDu via IFTTT

[naivelocus]

The 100-year-old challenge to Darwin that is still making waves in research

Wild Horizons/UIG via Getty

The shape of this chambered nautilus is one of many biological features that D’Arcy Thompson used maths to explain.

This year marks the centenary of what seems now to be an extraordinary event in publishing: the time when a UK local newspaper reviewed a dense, nearly 800-page treatise on mathematical biology that sought to place physical constraints on the processes of Darwinism.

And what’s more, the Dundee Advertiser loved the book and recommended it to readers. When the author, it noted, wrote of maths, “he never fails to translate his mathematics into English; and he is one of the relatively few men of science who can write in flawless English and who never grudge the effort to make every sentence balanced and good.”

The Dundee Advertiser is still going, although it has changed identity: a decade after the review was published, it merged with The Courier, and that is how most people refer to it today. The book is still going, too. If anything, its title — alongside its balanced and good sentences — has become more iconic and recognized as the years have ticked by.

The book is On Growth and Form by D’Arcy Thompson. This week, Nature offers its own appreciation, with a series of articles in print and online that celebrate the book’s impact, ideas and lasting legacy.

Still in print, On Growth and Form was more than a decade in the planning. Thompson would regularly tell colleagues and students — he taught at what is now the University of Dundee, hence the local media interest — about his big idea before he wrote it all down. In part, he was reacting against one of the biggest ideas in scientific history. Thompson used his book to argue that Charles Darwin’s natural selection was not the only major influence on the origin and development of species and their unique forms: “In general no organic forms exist save such as are in conformity with physical and mathematical laws.”

Biological response to physical forces remains a live topic for research. In a research paper, for example, researchers report how physical stresses generated at defects in the structures of epithelial cell layers cause excess cells to be extruded.

In a separate online publication (K. Kawaguchi et al. Nature http://dx.doi.org/10.1038/nature22321; 2017), other scientists show that topological defects have a role in cell dynamics, as a result of the balance of forces. In high-density cultures of neural progenitor cells, the direction in which cells travel around defects affects whether cells become more densely packed (leading to pile-ups) or spread out (leading to a cellular fast-lane where travel speeds up).

A Technology Feature investigates in depth the innovative methods developed to detect and measure forces generated by cells and proteins. Such techniques help researchers to understand how force is translated into biological function.

Thompson’s influence also flourishes in other active areas of interdisciplinary research. A research paper offers a mathematical explanation for the colour changes that appear in the scales of ocellated lizards (Timon lepidus) during development (also featured on this week’s cover). It suggests that the patterns are generated by a system called a hexagonal cellular automaton, and that such a discrete system can emerge from the continuous reaction-diffusion framework developed by mathematician Alan Turing to explain the distinctive patterning on animals, such as spots and stripes. (Some of the research findings are explored in detail in the News and Views section.) To complete the link to Thompson, Turing cited On Growth and Form in his original work on reaction-diffusion theory in living systems.

Finally, we have also prepared an online collection of research and comment from Nature and the Nature research journals in support of the centenary, some of which we have made freely available to view for one month.

Nature is far from the only organization to recognize the centenary of Thompson’s book. A full programme of events will run this year around the world, and at the D’Arcy Thompson Zoology Museum in Dundee, skulls and other specimens are being scanned to create digital 3D models. Late last month, this work was featured in The Courier. One hundred years on, Thompson’s story has some way to run yet.

— Nature News & Comment

[endevagames]

Looking back at what I previously wrote when documenting the development of my game, currently only known as project Dunia, I realized that I barely went into detail into the actual process that I went about when generating the terrain. In order to help some of you actually create the terrain, I will go into more detail about how I did it and how you could replicate it.

Generating the actual terrain

There are plenty of methods that are used when generating terrains and many algorithms that you can use. I would recommend using either Perlin noise or simplex noise as there seems to be a ‘port’ of them for most languages. GameMaker users such as me can find Perlin noise or simplex noise on the old GameMaker Forums or on the GameMaker Marketplace. In my project, I used 2D simplex noise (note 3D simplex noise is covered by a patent).

You will need to set a fixed width and height for your terrain. Generally, you could use 2D simplex noise as a primarily 2D function that gave you a value that you would put against a threshold in order to determine whether or not a tile would be there. In my scenario, however, I decided to use it as a 1D function whereby I would be theoretically producing a heightmap. The y coordinate of the point in question would then be compared to the height of the terrain at its x-position.

In order to get features such as overhangs, this method isn’t enough. It would produce a generally flat terrain. What you will be required to do in order to have overhangs is to distort the x-value of the coordinate using another simplex noise fractal. For example, if we were at point (1,1) on the map and the height our fractal states the terrain is at x = 1 is 10, we could distort the x-value using a fractal so it would appear that we are checking for a value at x = 2 rather than 1 which would give us a different height to check against the y coordinate that we have. This gives us the possibility of having varied terrain but be careful about the max factor that you can distort in the x-value as larger values can create holes in your terrain and annoying floating islands.

  Your first terrain is likely to look really plain

  Caves

Previously, I discussed how I used cellular automaton to produce the caves in my game. This became a frustrating endeavor since the caves weren’t shaped with any form of control which left parts such as cave openings too large at times or caves that felt too hollow. After discussing on cave generation methods with MishMash from the YoYoGames Forums (Seriously check out his team’s game Vitality RPG), I settled on using a modified form of drunkard’s walk.

How this works in my game is that we create a temporary array of the map and set the whole array to 0. We then use a 2d simplex noise fractal along the x-coordinate (we ignore the y-coordinate just as we did when generating a height map). The value that that function returns is compared to a threshold and if it exceeds the threshold, we can start building a cave.

Each cave technically starts at the absolute top of the array but they only become ‘visible’ once in contact with the terrain. Here we start carving the terrain. Each step, we set a radius of values around where our current pointer is at in the array to a value that you can recognize as a cave (it is up to you when drawing the cave to distinguish which values stand for caves and which values stand for normal terrain). At the end of each step, we move downwards by the same radius we used above whilst also arbitrarily moving either to the left, right or staying put. We repeat this process every time we generate a new cave and the results are much better than before.

It’s hard to see from the pictures above (upper pictures are old, lower pictures are new), the caves have more of a controlled form with the new method I used to generate caves. This is crucial for my project as some of the caves that I will be generating will be required to have entrances to dungeons in them. It’s a lot more easier to place a door or an item in a structure that despite being random, you still have full control over.

What am I up to now?

Well progress has really been at a halt for this project and I hate to be fulfilling the stereotype of overambitious indie developers but school plus a general lack of motivation has kept me at bay for quite too long. Regardless, I am back to developing this and I’m currently learning 2d procedural animation so I hope I can share something with you soon.

Please leave a comment!

For us content creators, we really appreciate it when we find out that we aren’t just shouting out into a void and that we have given you some food for thought so please don’t hesitate to comment (including criticism). How would you approach this? Did this help you at all?

Generating 2d terrain - In Depth #gamedev #indiedev #gamemaker Looking back at what I previously wrote when documenting the development of my game, currently only known as project Dunia, I realized that I barely went into detail into the actual process that I went about when generating the terrain.

[mobiletaggingart]

CELLULAR AUTOMATON SERIE

3D-fractal, 3D-print, PLA plastic 10″×10″. 2017. Digital art

PEDRO MORALES

A cellular automaton is a collection of “colored” cells on a grid of specified shape that evolves through a number of discrete time steps according to a set of rules based on the states of neighboring cells.

THE SACRED HEART CELLULAR AUTOMATON SERIE 3D-fractal, 3D-print, PLA plastic 10"×10". 2017. Digital art PEDRO MORALES A cellular automaton is a collection of "colored" cells on a grid of specified shape that evolves through a number of discrete time steps according to a set of rules based on the states of neighboring cells.