#''a two dimensional square becomes a cube which becomes a 4d shape''

[fantasmalresplendent]

Listening to this episode of Worlds Beyond Number is like:

Brennan says some crazy shit

I have to pause to take in that crazy shit

I un-pause the podcast, ready to move on

Brennan says even crazier shit not 15 seconds later

My guy! Let me live!!!

[inknerdblog]

Is Spinel 4 Dimensional?

https://my-little-universe.fandom.com/wiki/Spinel

Finally, after hours of research, analysis, and a ridiculous amount of editing all with only 5 hours of sleep I have completed my masterpiece! The idea I found in the two previous posts was interesting, to say the least. So, I just had to run this idea into the ground with the power of the Internet!

WARNING: EXTREMELY NERDY CONTENT BELOW

Side effects of content consumption may include second-hand knowledge on physics and geometry, rant-induced headaches, accidental consumption of glorified nerd spaghetti, and unintentional theory crafting.

READER’S DISCRETION IS ADVISED.

Definition of 4th Dimension:

Before determining if Spinel is 4 dimensional, we need to define the 4th dimension. From a math perspective, it’s just another coordinate. Just like the x-, y-, and z-coordinates or length, height, and width on a 3-dimensional coordinate plane, adding a fourth coordinate gives you a fourth dimension to move along. 

Of course, that doesn’t exactly explain what the 4th-dimension IS. In simplest terms, a 4D shape is just a bunch of 3D shapes fused together (which is very fitting for Steven Universe). Take a cube for example. 

https://www.transparentpng.com/cats/lines-1247.html (edited)

A 1-dimensional cube is just a line. 

https://www.vexels.com/png-svg/preview/139342/basic-square-outline (edited)

Fuse 4 lines and you make a 2D cube or a square. 

https://www.vexels.com/png-svg/preview/155839/stroke-cube-icon (edited)

Fuse 6 squares and you make a 3D cube which is obviously just a cube.

http://centerofmathematics.blogspot.com/2015/03/throwback-fact-magic-squares.html (edited)

By this logic, a 4D cube, known a tesseract, is a fusion of 8 cubes. These are many ways to draw a tesseract including a view from one of its axes like seen above.

A full view of a tesseract can be very hard to see in a diagram. A fusion of 8 cubes means there are...a square has 4 lines...multiply by 6 squares per cube...times 8 cubes per tesseract… THAT’S LIKE ALMOST 200 LINES (192 to be exact). Luckily there’s a way to kind of see what a 4D cube would look like.

https://www.pitt.edu/~jdnorton/teaching/HPS_0410/chapters/four_dimensions/index.html (edited)

You essentially just have to cross your eyes to “fuse” these figures together. If you have trouble, just try to look slightly over it.

Another way to interpret the tesseract is with a “beach ball” cube.

https://researchblog.duke.edu/2017/04/26/visualizing-the-fourth-dimension/

This is just a cube that has been printed along the sides of a sphere to give it a bloated appearance.

https://researchblog.duke.edu/2017/04/26/visualizing-the-fourth-dimension/

When shining a light on its north pole, the cube creates a 2D plane.

https://researchblog.duke.edu/2017/04/26/visualizing-the-fourth-dimension/

This can then be converted into a 3D object and connected with circular faces.

4 Dimensional Being Abilities:

The easiest way to explain the abilities of a being that is 4-dimensional is to consider how a 2-dimensional being would interpret us as 3-dimensional beings. In a 2-dimensional world, 3D beings would only be cross-sections. This would make us appear to only be blobs of shapes floating in mid-air.

https://store.steampowered.com/app/619210/4D_Toys/

Moving into the 3rd dimension (i.e. a different z-coordinate than the one the 2D world is in) would make us “disappear.”

With this in mind, a 4D being would essentially be extremely powerful. They would be able to see everything in the 3rd dimension at once. They could “disappear” by moving into the 4th dimension. Heck, they could remove your heart without cutting you open, much like a 3D being could remove a dot from a circle without cutting it.

So Could Spinel Be 4-Dimensional?

Short answer: no. With what we’ve seen from the Movie and Future, Spinel could not be 4-dimensional.

Spinel would be super OP. She would have no problem defeating all the Diamonds AT ONCE let alone Steven without any of his powers except the power to stick to smooth surfaces, apparently...

https://makutas-chronicle.tumblr.com/post/187538461056/spinel-garnet-and-true-kinda-love (You should check out this post. It brings up some really good points about the song “True Kind of Love”.)

Her whole reason for attacking Earth would be completely pointless! As a 4D being, she would have SEEN what happened to Pink Diamond and left the Garden before the show even started.

Even if gems had the technology and the massive amount of resources to create a being beyond their comprehension, what would be the point? Spinel was only meant to be a playmate. If they wanted Spinel to also have surveillance on Pink that could MAYBE justify creating a gem as complex as her. However, that still gives Spinel enough power to overthrow the Diamond Authority BY HERSELF. 

The only way the events of the movie could take place AND Spinel could be this powerful is if she spent her time in the Garden suppressing her ability to avoid peaking while playing the “game” with Pink.

https://www.youtube.com/watch?v=GBTN4ewBPQc

Maybe after thousands of years of suppressing her power, she lost the ability to use it? But then how did she get the Injector if not by walking into the 4th dimension? When she reset, wouldn’t she regain the ability without the memory of suppressing it? Wouldn’t she constantly morph and contort whenever she moved as her ability becomes goes haywire!?

https://www.youtube.com/watch?v=dyhqb1ciB2s

I think it’s more likely that she can only infer the 4th dimension. Kind of like how we infer the 3rd dimension. 

Yeah, apparently humans can’t actually see into the 3rd dimension. We only see the 2nd projections of 3D shapes and use light, shadows, and our position relative to objects around us to interpret depth.

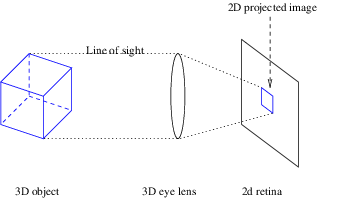
https://researchblog.duke.edu/2017/04/26/visualizing-the-fourth-dimension/

Maybe Spinel just has advanced retinas. Maybe she can see into the 3rd dimension and infer the 4th.

https://researchblog.duke.edu/2017/04/26/visualizing-the-fourth-dimension/

Yes, she wouldn’t be able to flatten her gem or be the next dictator of all gem-kind, but it could explain what we see her do. She could walk around without half her head being gone one second and her leg the next.  She could have seen where the Injector and the Rejuvenator were through the 4th dimension. She maybe could have even navigated into the 4th dimension with her advanced vision and some effort.

The only thing this theory can’t explain is where that Rejuvenator came from and why it was so close to the Garden...Did Pink have a backup plan in case Spinel tried to follow her!?

https://vocal.media/geeks/everything-you-need-to-know-for-steven-universe-the-movie-part-2

And that’s it! If you made it this far, you’re just as hopelessly nerdy as I am! Only you didn’t spend hours of your life writing a 10-page paper on whether a fictional character could take over the universe...

Special thanks to  a-second-chance-su-au for inspiration. I never would have made this nerd spaghetti if you hadn’t handed me the ingredients! Check them out if you like SU AUs featuring CG Spinel.

Do you have any suggestions? Criticisms? Ideas you want me to obsess over explore? Did I miss something? Do you have a counter-theory? Then just send in an ask! I’ll try my best to respond. Have a nice day and drink your energy beans! 

References (Order of Appearance I think... I may have messed up the order):

http://eusebeia.dyndns.org/4d/vis/01-intro (Humans Only See in 2D)

https://plus.maths.org/content/richard-elwes (4D math perspective)

https://www.pitt.edu/~jdnorton/teaching/HPS_0410/chapters/four_dimensions/index.html (Shape Fusion)

https://researchblog.duke.edu/2017/04/26/visualizing-the-fourth-dimension/ (“Beach Ball” Tesseract)

http://sprott.physics.wisc.edu/pickover/fourth.html (3D Beings to 2D Beings = 4D Beings to 3D Beings)

[thousandmaths]

Dynkin Diagrams and a Proof Sketch

This is the third and final post (1 2 3) in our three-part sequence on classifying finite Coxeter groups. However, don’t despair! Curious readers can find out more about finite Coxeter groups by picking up the main sequence (1 2 3 4 5 6 7 8 9) at Post 6 :)

In the last post, we dove into the history behind Coxeter groups to understand— if not explain— about half of the weirdness in the classification. This post is devoted to the other half :)

------

Cleaning up the Classification

At the end of the last post, we mentioned that Dynkin’s new idea of the “simple root” permitted a cleaner way to classify semisimple Lie algebras. It didn’t take long at all for people to apply this idea to the Coxeter systems. The result is a much more memorable rewriting of the classification theorem:

Theorem (Coxeter-Dynkin). Every finite irreducible Coxeter system corresponds to exactly one of the following diagrams.

(source (for picture))

I’ve explained how these Coxeter-Dynkin diagrams* correspond to reflection groups previously, and their relationship to Coxeter groups is very similar.

[ * I will call these Dynkin diagrams in this sequence, although this term is sometimes reserved exclusively for the related Lie theoretic objects. ]

Each dot in the diagram represents a generator; so in particular the number of dots is the rank of the system. As we noted in the last post, most $m_{s,t}$ are $2$, and most of the $m_{s,t}$ which are not $2$ are $3$. So the diagram hides all of those “boring” numbers, and only lists the unusual ones.

whenever there is no line between two dots, that means $m_{s,t}=2$.

whenever there is an unlabeled line between two dots, that means $m_{s,t}=3$.

whenever there is a labeled line between two dots, then $m_{s,t}$ is equal to the label.

You can try your hand at converting one of the Dynkin diagrams above into its $m_{s,t}$ information, perhaps for $B_4$, and see that you really do get the same thing as in the longform description in the first post.

So this really is just a “translation”: we haven’t removed any of the inherent weirdness in the result; even down to preserving the historical idiosyncrasies. But it’s certainly a lot more memorable this way! That’s why I said this was a “psychologically useful” simplification at the end of the last post. And, as it turns out, the graph-theoretic nature of the Dynkin diagram shows up in the proof in a way which is a bit awkward to translate back to the original setting! 

------

What’s The Plan? A Sketch of a Proof

We can prove the classification of finite irreducible Coxeter groups by following this outline (which is not mine). Note that, with the exception of Step 1, each of these steps requires quite a bit of effort to prove.

There must exist $m_{s,t}$ for every pair of generators $s$ and $t$. Remember that for general Coxeter groups we don’t have to do this, but if we don’t, then all of the words $st, stst, ststst, stststst, ststststst,$ and so on, are all non-equivalent.

If there is a loop in the diagram, we show that there are infinitely many non-equivalent words. So we cannot have loops. Also, if the diagram is not connected, the Coxeter system is reducible. (In graph-theoretic language, the Dynkin diagram is therefore a tree.)

We note that all regular polytopes give rise to a Dynkin diagram, and we use the classification of regular polytopes. This accounts for Types A and B; also Types F, G, H, and I. After that, we show that any other valid Dynkin diagram must have a point with three lines connecting to it.

Show that if there is both such a point and any labeled edge (i.e. $m_{s,t}>3$ for any generators) then we can find infinitely many non-equivalent words. So this can’t happen, and hence outside of Types ABFGHI, all edges must be unlabelled.

Show that there is only one such point (as in Step 3); the remainder of the proof then focuses on this point.

If $a,b,$ and $c$ are the lengths of the “paths” that start at this point (including the point itself), show that $\frac1a+\frac1b+\frac1c > 1$. This excludes every conceivable diagram that isn’t on the list we gave above.

Finally, we need an explicit construction to show that Types D and E are in fact finite.

We can now answer the questions we had earlier about why the patterns in the exceptional types EFGH (and I) seem to just... stop.

Step 3 explains why the Types F and H patterns do not continue:

$F_4$ corresponds to the $24$-cell, an object unique to four-dimensional geometry,

$H_2, H_3, H_4$ correspond to the pentagon, dodecahedron, and the 120-cell, which do not have analogues in dimensions five or higher.

and Step 6 explains why the Type E pattern does not continue.

In the language of the proof, the Type E pattern is that $a=2$ and $b=3$.

But basic algebra says that $\frac12+\frac13+\frac1c > 1$ is only true when $c<6$, and so the length of the long leg can be at most $5$.

Steps 3 and 4 together also explain why $m_{s,t}$ is so commonly $2$ or $3$: if the diagram’s shape is interesting at all, then it can’t be anything else, and if it’s just a straight line then you have very strong restrictions on the labels.

Of course, you can certainly ask for more details. The formula used in Step 6 comes from evaluating a certain determinant, and it’s probably not very productive to see that derivation laid out in detail. But I would like to make an extended comment on the geometric theorem used in Step 3.

------

Geometry Again: Classifying Regular Polytopes

A polytope is a high-dimensional generalization of polygons and polyhedra. Regularity is a bit trickier to define, but it comes from the intuitive idea of “looks the same everywhere”:

A polygon is regular if all of its sides have the same length and all of the edges make the same angle at each vertex.

A polyhedron is regular if all of its faces are regular polygons, all of its edges are the same length, and the same number of faces meet at each vertex.

In two dimensions, we know there are infinitely many polygons. But Greek mathematicians famously proved that there are only five regular polyhedra. Their proof goes like this: 

If you want the polygons to “close up”, then they had better meet at an angle which is less than 360º. If they meet at exactly 360º, then they tile the plane, so the shape never closes. And if they meet at more, then they actually get further away from each other; that’s even worse!

You have to have at least three polygons meet at each vertex, otherwise the shape collapses to be two-dimensional.

Now do some arithmetic:

Triangles have angle 60º, and to get $60n<360$ you can put at most 5 of those at each vertex.

Squares have angle 90º, and to get $90n<360$ you can put at most 3 at each vertex.

Pentagons have angle 108º, and to get $108n<360$ you can put at most 3 at each vertex.

Hexagons have angle 120º, so you can’t even put 3 at each vertex.

As you add more sides, the angle always increases, so you can’t use anything with more sides than a pentagon.

This gives you five possible options for how vertices look: either 3, 4, or 5 triangles, or 3 squares, or 3 pentagons.

Finally, check that all of these are actually possible.

(source)

The proof in higher dimensions is more technical, but the argument has the same spirit. In 4D, we get analogues of all five polyhedra, plus the 24-cell, which, as I suggested above, is a rather weird shape that doesn’t translate well to our 3D intuition. 

(source; the 24-cell is the yellow one)

You would think that as dimensions increase far beyond our ordinary experience, these sorts of unintuitive creatures would start popping up all over the place. But amazingly, the equations in dimension 5 and above suddenly become extremely restrictive. In the end, the only things that survive in high dimension are the analogues of the cube, the tetrahedron, and the octahedron.

These geometric restrictions that ultimately descend all the way down to the level of Dynkin diagrams. Therefore, the reason that the exceptional FGH patterns only exist for small rank is because the exceptional polytopes only exist in small dimension.

[ Previous ] [ Post 3 ] and [[ “Next”: Post 6 of the Coxeter sequence ]]

[mathandnumberystuff]

Higher-dimensional Pascal’s Triangle

Most readers of this blog are probably familiar with Pascal’s Triangle. If not, it consists of rows of integers where the spaces between numbers in one row are directly above numbers in the next row down. The first row is made of two infinitely long strings of 0s separated by a 1. Each number on a subsequent row is derived by summing two adjacent numbers on the previous row, so each row contains one more nonzero term than the previous one. The zeroes aren’t written in the finished diagram, so it looks like the top of an infinitely large triangle:

It is well known that the rth number (using zero-based indexing) on the nth row (also using zero-based indexing) is the value nCr, read as “n choose r”, a function which computes the number of ways to choose r objects from a set of n, where the order of the chosen objects doesn’t matter. However, there are other ways to think of this operation. One of those ways is to consider a string of n objects consisting of r copies of one object and n - r copies of another object. Then nCr is the number of permutations of the string.

It is also helpful to stop thinking of it as a function of the total length of the string and the number of permutations. Instead, it should be thought of in terms of the number of objects of each type. If r objects are of type 0 and s objects are of type 1, then there are (r + s)Cr ways to order the string. Let’s call this value A(r, s).

Also, from now on in my examples, the “type 0″ objects will all be the number 0, and the “type 1″ objects will be the number 1, so as to match the index of the functional argument determining the number of copies of that object. Now the strings of objects can be considered lists of numbers.

One of the benefits of this new understanding is that the identity nCr = nC(n-r) can now be expressed as A(r, s) = A(s, r). Under the visualization, all this means is that the number of lists of r zeroes and s ones is the same of the number of lists of r ones and s zeroes. Another benefit is that the cases where nCr = 0 (where the value lay “outside” of the triangle) now become the cases where one of r or s is negative but r + s ≥ 0. The values that form the triangle itself come from the cases where r and s that are both nonnegative.

Now we can create a grid of all possible values of A for nonnegative values of r and s by plotting the value A(r, s) onto the point (r, s) in R^2:

This is Pascal’s triangle as seen from a different angle, In fact, it now looks more like the corner of a square, and this visualization as a quadrant of a plane will be useful when we extend the concept to higher dimensions. In Pascal’s triangle, the nth row of the triangle was the set of terms such that r + s = n. This line cuts a cross section through the grid perpendicular to the line r = s.

Three dimensions

Now that we have constructed Pascal’s triangle with a function that gives the number of orderings of zeroes and ones in various amounts, one might wonder what we can construct similarly from a function computing the number of orderings of three numbers. Let’s call this function A(r, s, t), where there are r, s, and t objects of each type. It will be understood as the number of ways that r zeroes, s ones, and t twos can be put into a list. Obviously the value of A(r, s, t) remains the same however r, s, and t are permuted.

If we plot the values A(r, s, t) on the points in 3-space (r, s, t) for nonnegative r, s, t, we get what looks like the corner of a cube. What happens when we set r + s + t, the total number of items to order, to a constant? Will we get a layer from a 3D version of Pascal’s triangle?

The points (r, s, t) in R^3 such that r + s + t is a constant integer form a plane perpendicular to the line r = s = t. The subset of this plane for positive r, s, t forms an equilateral triangle, whose vertices are on the r, s, and t axes. The points in this triangle such that r, s, and t are integers are arranged like the vertices of a triangular tiling, and each point is sqrt(2) away from its neighbors.

Under this geometric interpretation, this is the structure analogous to the nth row of Pascal’s triangle. It forms a triangle of points, n + 1 along each outer edge, and each point is associated with a trio of coordinates (r, s, t) from the original lattice and a corresponding value A(r, s, t) of the function.

Here is what the first 6 layers look like:

For each triangle, the left, right, and bottom edges contain the points where r, s, and t are 0 respectively. (Actually, the edges could be chosen in any order for this.) The lines of points through the triangle, parallel to one of these edges and x neighbors away from it, are the points whose coordinate corresponding to the direction of the edge (left, right, or bottom) has the value x. Of course, only two coordinates are required to label every point uniquely, but using three coordinates emphasizes the symmetry between the three values in the function; in fact, each permutation of r, s, and t maps points to other points and transforms the triangle onto itself! This is a beautiful way to demonstrate that the group of all permutations of three elements is the same as the symmetry group of an equilateral triangle!

So how do you compute these numbers anyway?

The formula for A(r, s, t) is A(r, s)*A(r + s, t). Of course, it is also A(r, t)*A(r + t, s), and A(s, t)*A(s + t, r). Intuitively, A(r + s, t) represents the number of lists that can be made from t twos and r + s blanks to be filled in with 0 and 1, and A(r, s) represents the number of ways the blanks in each list can be filled by r zeroes and s ones.

In practice, the nth layer can get computed from the first n + 1 layers in Pascal’s triangle. First un-flatten the square corner as seen above back into a triangle corner with 60-degree angles, and then multiply each member of the xth layer (where x goes from 0 to n) by A(n - x, x) = nCx. This is fun to do, as it doesn’t make the S3 symmetry of the resulting arrangement of numbers obvious until you actually try it.

Each layer can be constructed from the previous layer

There is also another way to construct each layer. In Pascal’s triangle, each row below the zeroth can be constructed by summing pairs of adjacent numbers on the previous row. Specifically, A(s, t) = A(s - 1, t) + A(s, t - 1). Even the 1s on the outside are created by summing 1s on the previous row with invisible zeroes neighboring them. (A(s, t) = 0 when s or t is negative.)

In the 3D version, triples of adjacent terms are of two types. One type, with coordinates (r - 1, s - 1, t), (r - 1, s, t - 1), (r, s - 1, t - 1), forms the vertices of a triangle pointing down. The other type, with coordinates (r - 1, s, t), (r, s - 1, t), (r, s, t - 1), forms the vertices of a triangle pointing up.

If the next layer gets made by summing both types of triples, it will have twice the density of numbers as the previous layer:

But if we sum only the triples pointing up, the ones with coordinates (r - 1, s, t), (r, s - 1, t), (r, s, t - 1) and put the results in the middles of the triangles, then the result will be the next layer, and the numbers will have coordinates (r, s, t) for all values of r, s, and t that sum to the layer number.

The fact that A(r - 1, s, t) + A(r, s - 1, t) + A(r, s, t - 1) = A(r, s, t) is obvious when we consider the fact that A(r, s, t) represents the number of strings of r 0s, s 1s, and t 2s and these consist of:

A(r - 1, s, t) strings where a 0 is followed by r - 1 0s, s 1s, and t 2s

A(r, s - 1, t) strings where a 1 is followed by r 0s, s - 1 1s, and t 2s

A(r, s, t - 1) strings where a 2 is followed by r 0s, s 1s, and t - 1 2s.

Sum of each layer

In Pascal’s triangle, the numbers in the nth row sum to the value 2^n. This can be explained by the fact that there are 2^n strings of length n made of only 0s and 1s. Similarly, as there are 3^n strings of length n made of only 0s, 1s, and 2s, each layer of Pascal’s tetrahedron sums to a power of 3.

Higher dimensions

The function A(r, s, t) can be generalized to any number of arguments. Really, it can be thought of as taking in a tuple, of any length, of integers as arguments. For integers r, s, t, ... z, it can be defined as A(r, s, t, ... y, z) = A(r, s, ... y) * A(r + s + ... + y, z), and for two arguments, A(r, s) is defined as (r + s)Cr. The nth layer of the structure can be found by taking the set of points (r, s, ... z) whose coordinates that sum to n, and associating to each point with tuple T of coordinates the value A(T), which will be positive if no coordinate is negative and 0 if at least one of them is negative but the sum is still positive.

Just as the layers of the 3D Pascal’s triangle are shaped like equilateral triangles, the layers of the higher dimensional analogs will also be shaped like a regular simplex, a shape which is just a pyramid of a regular simplex from the previous dimension, where all edges are the same length. For example, the 3D simplex is a tetrahedron, and the 4D simplex is a pentachoron.

In d dimensions, the lattice of points (r0, r1, r2, r3, ... r(d - 1)) where each r-value is an integer, forms the vertices of a d-hypercubic tessellation of edge length 1. The subset of points where the coordinates are required to sum to an integer n form the vertices of a (d - 1)-simpletic tessellation of edge length √2. The points on this layer with nonnegative coordinates form a subset of this lattice in the shape of a (d - 1)-dimensional simplex. From now on, these points will be what I mean when I refer to a “layer” of the figure.

The points in the nth layer of the d-dimensional lattice (which itself is (d - 1)-dimensional, of course) can be decomposed into a stack of n + 1 (d - 2)-dimensional sub-layers of points in the shape of (d - 2)-dimensional simplices, ranging from n + 1 points per edge down to 1 point per edge (at 1 point per edge, there is also only one point in the entire sub-layer; this is the tip of the layer). This stack constructs the (d - 1)-dimensional simplex as a pyramid of a (d - 2)-dimensional simplex.

How to find the numbers in each layer

The same method mentioned above, of constructing the nth layer of 3D Pascal’s pyramid from the first n + 1 layers of Pascal’s triangle, also works for higher dimensions. For the nth layer of the d-dimensional pyramid, stack the first n + 1 layers of the (d - 1)-dimensional pyramid (the 0th to the nth layer), and multiply each number on the x-th layer by A(n - x, x) which is just equal to nCx.

For example, here are the first 5 layers of 3D Pascal’s triangle:

And here are the cross-sections of layer 4 in 4D Pascal’s triangle:

Except this does not work exactly from a geometrical standpoint, because in the first n layers of Pascal’s pyramid, adjacent points in neighboring layers are only 1 unit apart, instead of the √2-unit distance between adjacent points from the same layer. Instead of a regular simplex for each layer, this method simply produces a cut-off corner of a hypercube! To fix this problem, all that is needed is to “stretch” the pyramid by increasing the distance between neighboring layers (now “sub-layers” as part of a layer themselves) until all adjacent points have the same distance of √2 between them.

Each layer can also be constructed by adding terms from the previous layer.

To understand how this would work, you have to realize that in (d + 1)-dimensional Pascal’s triangle, there are d different types of “gaps” between points. The x-th type is found by taking the coordinates of a point x layers ahead and finding all possible ways to subtract 1 from x of those coordinates. For example, in 4D Pascal’s triangle, a gap of type 2 would be made of these points: (r - 1, s - 1, t, u), (r - 1, s, t - 1, u), (r - 1, s, t, u - 1), (r, s - 1, t - 1, u), (r, s - 1, t, u - 1), (r, s, t - 1, u - 1) - there is one gap for each possible set of values of r, s, t, and u.

Gaps of type 1 form the vertices of a simplex, flipped relative to the orientation of the layer itself. The numbers from these points get added to form the number in the next layer, at the center of the gap. Each point belongs to exactly d+1 of these gaps, so the sum of the terms from the (n + 1)st layer is (d + 1) times the sum of the terms from the nth layer. The initial layer sums to 1 (as 1 is the only nonzero term in that layer), and therefore the nth layer sums to the value (d + 1)^n (again, the initial layer must be counted as the 0th, not the 1st).

Also, not all these gaps are the same shape. Some form the vertices of a simplex, some the vertices of a rectified or birectified simplex, etc. In fact, these gaps are the shapes of the facets of the simpletic tessellation whose vertices are the points in a single layer.

So, to review:

(d + 1)-dimensional Pascal’s triangle is a collection of points in (d + 1)-dimensional space with coordinates (r, s, t, ... y, z) where each coordinate is a positive integer.

Each point is associated with a value A(r, s, t, ... y, z), where A(r, s) = (r + s)Cr = (r + s)!/(r!*s!) and A(r, s, ... y, z) = A(r + s + ... + y, z).

The nth layer of this triangle is the set of points for which r + s + ... y + z is a constant.

The points in a single layer are the vertices of a d-dimensional simplectic tessellation (d-honeycomb) of edge length √2 -- the 2D simplectic tessellation is the triangular tiling and the 3D simplectic tessellation is the tetrahedral-octahedral honeycomb.

The value of the point (r, s, ... y, z) can be found by summing the values of the points (r - 1, s, ... y, z), (r, s - 1, ... y, z) ... (r, s, ... y - 1, z), (r, s, ... y, z - 1).

Nice! Soon we’ll look at more properties of this triangle, like which numbers can appear where.