systems101

[systems101]

[systems101]

[systems101]

[systems101]

[systems101]

Graphs and decision trees in Python

A pair of nodes are connected by a single path.

Decision trees are great for finding solutions. The trunk is at the top and the the branches at the bottom - very Australian.

But, how are decision trees useful?

(Computer) networks require algorithms to move information around.

Financial networks - moving around money

Sewage networks - moving water around

Decision trees can determine which path to take when executing the algorithm that moves information.

Graphs

Graphs can capture interesting relationships with this data.

The min flow or max cut problem identifies which clusters in a graph have a lot of interaction between each-other but not with many (or any) other clusters.

Inference option. Is there a sequence of edges to get from A to B. Can I find the least expensive (meaning shortest) path?

The graph partition problem. Not all nodes have connections with every other node.

This is finding and isolating different sets of connections.

Min cut max flow - an efficient way of separating highly connected elements, the things that connect a lot in a sub-graph.

Graphs (graph theories) are used by us everyday in the forms of travel maps such as on the tube etc.

Di graph (directed graph) the edges pass in one direction - almost obvious, I know.

Nodes or vertices become points of intersections, places to make a choice or has terminals.

Edges would be connections between points - the roads on which we could drive. Each edge would have a weight.

Choices that remain:

What’s the expected time between a source and a destination?

What’s the distance between the two?

What’s the average speed of travel?

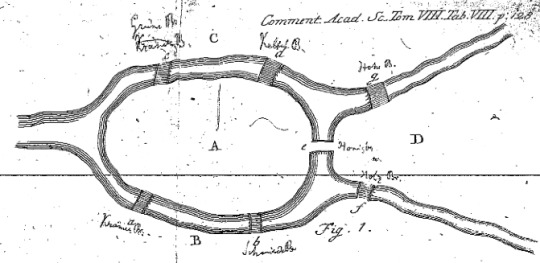
Thinking about navigation in graph systems incorporated within history from 1700′s. The image above is from ‘Solutio problematis ad geometriam situs pertinentis,’ Eneström 53 [source: MAA Euler Archive]

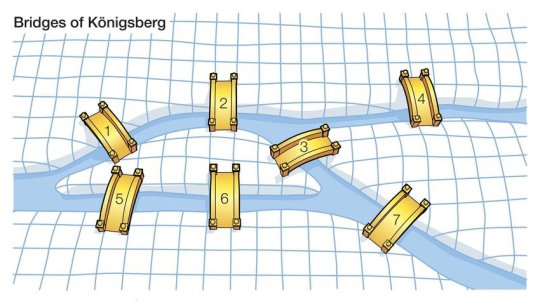
Bridges of Königsberg which has seven bridges that connect it’s rivers and islands - is it possible to take a walk that traverses each of the seven bridges exactly ONCE.

Leonhard Euler, a great Swiss mathematician said, “make each island a node, each bridge is an undirected edge”.

This eliminates irrelevant details about the size and focuses on the connections present, testing the point of crossing only once.

Euler’s Proof and Graph Theory

When reading Euler’s original proof, one discovers a relatively simple and easily understandable work of mathematics; however, it is not the actual proof but the intermediate steps that make this problem famous.  Euler’s great innovation was in viewing the Königsberg bridge problem abstractly, by using lines and letters to represent the larger situation of landmasses and bridges.  He used capital letters to represent landmasses, and lowercase letters to represent bridges.

This was a completely new type of thinking for the time, and in his paper, Euler accidentally sparked a new branch of mathematics called graph theory, where a graph is simply a collection of vertices and edges.

Today a path in a graph, which contains each edge of the graph once and only once, is called an Eulerian path, because of this problem. From the time Euler solved this problem to today, graph theory has become an important branch of mathematics, which guides the basis of our thinking about networks.

An easy graph would be: latitude and longitude

We want to extract things away from the graph so let’s represent the nodes as objects - using classes for these.

For now, the only information to store a name (which is currently just a string) inherits from the base Python object class.

Init function used to create instances of nodes.

Store inside each instance - in other words inside of self - under the variable name of whatever was passed in as the name of that node.

If we have ways to create things with a name we need ways to get them back out. So we can select it back out by asking an instance of a node “what is your name?” by calling getName, it will return that value.

Within the class edge we’d see:

class           Edge(object):

              def _init_(self, src, dest):

                    “““Assumes src and dest are nodes”““

                    self.src = src

                    self.dest = dest

             def getSource(self) :

                    return self.src

             def getDestination(self) :

                   return self.dest

            def _str_(self):

                  return self.src.getName() + ‘->’\

                            + self.dest.getName()

To print things out we’re just gonna print name. This allows us to create as many nodes as we like.

Edges connect up two nodes - allowing us to create a fairly straightforward construction of a class. Again, it’s going to inherit from the base Python object. To create an instance of an edge we will assume in the example above that the arguments passed in (source and destination) are nodes.

This is shown after the init function.

Not names, nodes - the actual instances of the object class. So inside of the edge, we set internal variables for each instance of the edge source and destination. The get source and destination allows us to get those variables back out. The last part asks to print the name of the source then an arrow and then the destination.

So here, given an instance of an edge, we can print it and it will retrieve the source or the node associated with the source inside the instance. The opened and closed parens () is used to call it.

From this we can decide how to represent the graph, starting with a di-graph which has edges that pass in once direction. Given all the sources and all the destinations we can just create an adjacency matrix.

[systems101]

[systems101]

Totally

[systems101]

Sadd that i know java and i'm starting c#

[systems101]

[systems101]

[systems101]

It works.

[systems101]

illiterate

[systems101]

Harsh but true!

[systems101]

When you have so much error that you become delusional.

[systems101]

[systems101]

Sign me up :D

[systems101]

😆😆😆😆😆😆