saltysockmonkey - Tumblr blog

saltysockmonkey · 4 years ago

Text

C3W4 Logistic Regression

My hypothesis is to find out if there is a relationship between life expectancy and urban rate. Life expectancy is the response variable, while urban rate is the explanatory variable. Since the gapminder data set variables are all quantitative, I needed to create a new data frame for the variables and bin each into 2 categories. The 2 categories are based on each variable's mean value. For each variable, 1 is >= the variable;s mean while all else is 0.

The initial regression model shows there is a statistical relationship between life expectancy and urban rate (p=1.632e-11, OR=12.10, 95% CI=26.98). Potential confounding factors include HIV Rate, alcohol consumption, and income per person.

It was found that incomerate has no statistical relationship in this model based on the p-value being 0.998. HIV Rate has a significant association with life expectancy (p=1.563e-10), but HIV has a lower OR (0.03). So HIV does have a significant relationship with life expectancy, but in an urban area the odds are low it will affect life expectancy. Alcohol consumption has a 3 times higher affect on life expectancy (OR=3.18, p=0.021, 95% CI=8.52) in urban areas even though it is less statistically significant than HIV Rate.

So the model output shows that life expectancy has significant statistical associations with urban rate and the confounding variables of HIV rate and alcohol consumption.

Complete OUTPUT

Life Expectancy Categories0 621 82Name: LIFE1, dtype: int64Urban Rate Categories0 711 73Name: URB1, dtype: int64HIV Rate Categories0 1151 29Name: HIV1, dtype: int64Alcohol Consumption Rate Categories0.00 761.00 68Name: ALCO1, dtype: int64Income Per Person Rate Categories0 1091 35Name: INC1, dtype: int64Optimization terminated successfully. Current function value: 0.525941 Iterations 6 Logit Regression Results ==============================================================================Dep. Variable: LIFE1 No. Observations: 144Model: Logit Df Residuals: 142Method: MLE Df Model: 1Date: Sat, 10 Oct 2020 Pseudo R-squ.: 0.2305Time: 09:21:51 Log-Likelihood: -75.736converged: True LL-Null: -98.420Covariance Type: nonrobust LLR p-value: 1.632e-11============================================================================== coef std err z P>|z| [0.025 0.975]------------------------------------------------------------------------------Intercept -0.8675 0.260 -3.336 0.001 -1.377 -0.358URB1 2.4935 0.409 6.095 0.000 1.692 3.295==============================================================================Odds Ratios for LIFE1 to URB1Intercept 0.42URB1 12.10dtype: float64COnfiedence Intervals for LIFE1 to URB1 Lower CI Upper CI ORIntercept 0.25 0.70 0.42URB1 5.43 26.98 12.10Optimization terminated successfully. Current function value: 0.541289 Iterations 7 Logit Regression Results ==============================================================================Dep. Variable: LIFE1 No. Observations: 144Model: Logit Df Residuals: 142Method: MLE Df Model: 1Date: Sat, 10 Oct 2020 Pseudo R-squ.: 0.2080Time: 09:21:51 Log-Likelihood: -77.946converged: True LL-Null: -98.420Covariance Type: nonrobust LLR p-value: 1.563e-10============================================================================== coef std err z P>|z| [0.025 0.975]------------------------------------------------------------------------------Intercept 0.8267 0.203 4.079 0.000 0.429 1.224HIV1 -3.4294 0.760 -4.510 0.000 -4.920 -1.939==============================================================================Odds Ratios for LIFE1 to HIV1Intercept 2.29HIV1 0.03dtype: float64COnfiedence Intervals for LIFE1 to HIV1 Lower CI Upper CI ORIntercept 1.54 3.40 2.29HIV1 0.01 0.14 0.03Optimization terminated successfully. Current function value: 0.622369 Iterations 5 Logit Regression Results ==============================================================================Dep. Variable: LIFE1 No. Observations: 144Model: Logit Df Residuals: 142Method: MLE Df Model: 1Date: Sat, 10 Oct 2020 Pseudo R-squ.: 0.08940Time: 09:21:51 Log-Likelihood: -89.621converged: True LL-Null: -98.420Covariance Type: nonrobust LLR p-value: 2.730e-05============================================================================== coef std err z P>|z| [0.025 0.975]------------------------------------------------------------------------------Intercept -0.3727 0.233 -1.597 0.110 -0.830 0.085ALCO1 1.4713 0.365 4.036 0.000 0.757 2.186==============================================================================Odds Ratios for LIFE1 to ALCO1Intercept 0.69ALCO1 4.35dtype: float64COnfiedence Intervals for LIFE1 to ALCO1 Lower CI Upper CI ORIntercept 0.44 1.09 0.69ALCO1 2.13 8.90 4.35Warning: Maximum number of iterations has been exceeded. Current function value: 0.517484 Iterations: 35 Logit Regression Results ==============================================================================Dep. Variable: LIFE1 No. Observations: 144Model: Logit Df Residuals: 142Method: MLE Df Model: 1Date: Sat, 10 Oct 2020 Pseudo R-squ.: 0.2429Time: 09:21:51 Log-Likelihood: -74.518converged: False LL-Null: -98.420Covariance Type: nonrobust LLR p-value: 4.710e-12============================================================================== coef std err z P>|z| [0.025 0.975]------------------------------------------------------------------------------Intercept -0.2770 0.193 -1.432 0.152 -0.656 0.102INC1 22.0742 9144.697 0.002 0.998 -1.79e+04 1.79e+04==============================================================================

Possibly complete quasi-separation: A fraction 0.24 of observations can beperfectly predicted. This might indicate that there is completequasi-separation. In this case some parameters will not be identified.Odds Ratios for LIFE1 to INC1Intercept 0.76INC1 3861007201.13dtype: float64COnfiedence Intervals for LIFE1 to INC1 Lower CI Upper CI ORIntercept 0.52 1.11 0.76INC1 0.00 inf 3861007201.13Optimization terminated successfully. Current function value: 0.411816 Iterations 7 Logit Regression Results ==============================================================================Dep. Variable: LIFE1 No. Observations: 144Model: Logit Df Residuals: 140Method: MLE Df Model: 3Date: Sat, 10 Oct 2020 Pseudo R-squ.: 0.3975Time: 09:21:51 Log-Likelihood: -59.301converged: True LL-Null: -98.420Covariance Type: nonrobust LLR p-value: 7.332e-17============================================================================== coef std err z P>|z| [0.025 0.975]------------------------------------------------------------------------------Intercept -0.6005 0.322 -1.863 0.062 -1.232 0.031URB1 2.0323 0.488 4.163 0.000 1.075 2.989ALCO1 1.1580 0.502 2.305 0.021 0.173 2.143HIV1 -3.4899 0.848 -4.114 0.000 -5.152 -1.827============================================================================== Lower CI Upper CI ORIntercept 0.29 1.03 0.55URB1 2.93 19.87 7.63ALCO1 1.19 8.52 3.18HIV1 0.01 0.16 0.03Code -------------------------------------------------------------------------

CODE import pandas as pdimport numpy as npimport seaborn as sbimport statsmodels.formula.api as smfimport statsmodels.stats.multicomp as multiimport scipy.stats as statsimport matplotlib.pyplot as plt # bug fix for display formats to avoid run time errorspd.set_option('display.float_format', lambda x:'%.2f'%x) gmdata = pd.read_csv('gapminder.csv', low_memory=False) ### Data Management ### # convert to numericgmdata.lifeexpectancy = gmdata.lifeexpectancy.replace(" " ,np.nan)gmdata.lifeexpectancy = pd.to_numeric(gmdata.lifeexpectancy)gmdata.urbanrate = gmdata.urbanrate.replace(" " ,np.nan)gmdata.urbanrate = pd.to_numeric(gmdata.urbanrate)gmdata.incomeperperson = gmdata.incomeperperson.replace(" " ,np.nan)gmdata.incomeperperson = pd.to_numeric(gmdata.incomeperperson)gmdata.alcconsumption = gmdata.alcconsumption.replace(" " ,np.nan)gmdata.alcconsumption = pd.to_numeric(gmdata.alcconsumption)gmdata.hivrate = gmdata.hivrate.replace(" " ,np.nan)gmdata.hivrate = pd.to_numeric(gmdata.hivrate) sub1 = gmdata[['urbanrate', 'lifeexpectancy', 'alcconsumption', 'incomeperperson', 'hivrate']].dropna() ## Drop all rows with NANsub1.lifeexpectancy.dropna()sub1.urbanrate.dropna()sub1.hivrate.dropna()sub1.incomeperperson.dropna()sub1.alcconsumption.dropna() #data check#a=sub1#print(a) #print("Life Expectancy Deviation")#desc1=gmdata.lifeexpectancy.describe()#print(desc1) #print("Urban Rate Deviation")#desc2=gmdata.urbanrate.describe()#print(desc2) #print("HIV Rate Deviation")#desc3=gmdata.hivrate.describe()#print(desc3) #print("Alchohol COnsumption Deviation")#desc4=gmdata.alcconsumption.describe()#print(desc4) #print("Income Rate Deviation")#desc5=gmdata.incomeperperson.describe()#print(desc5) # build bin for response categoriesdef LIFE1(row): if row['lifeexpectancy'] >= 69.75: return 1 else: return 0 print ("Life Expectancy Categories")sub1['LIFE1'] = gmdata.apply (lambda row: LIFE1 (row),axis=1)chk1 = sub1['LIFE1'].value_counts(sort=False, dropna=False)print(chk1)#def URB1(row): if row['urbanrate'] >= 56.77: return 1 else: return 0print ("Urban Rate Categories")sub1['URB1'] = gmdata.apply (lambda row: URB1 (row),axis=1)chk2 = sub1['URB1'].value_counts(sort=False, dropna=False)print(chk2)#def HIV1(row): if row['hivrate'] >= 1.94: return 1 else: return 0print ("HIV Rate Categories")sub1['HIV1'] = gmdata.apply (lambda row: HIV1 (row),axis=1)chk3 = sub1['HIV1'].value_counts(sort=False, dropna=False)print(chk3)#def ALCO1(row): if row['alcconsumption'] > 6.69: return 1 if row['alcconsumption'] <6.70: return 0 print ("Alcohol Consumption Rate Categories")sub1['ALCO1'] = gmdata.apply (lambda row: ALCO1 (row),axis=1)chk4 = sub1['ALCO1'].value_counts(sort=False, dropna=False)print(chk4)#def INC1(row): if row['incomeperperson'] >= 8740.97: return 1 else: return 0print ("Income Per Person Rate Categories")sub1['INC1'] = gmdata.apply (lambda row: INC1 (row),axis=1)chk5 = sub1['INC1'].value_counts(sort=False, dropna=False)print(chk5) #Check Bins#print(sub1) ###End Data Managament## ## Logistic Regression for individual variables against Life Expectancy### logistic regression with URB1 ratelreg1 = smf.logit(formula = 'LIFE1 ~ URB1', data = sub1).fit()print (lreg1.summary()) # odds ratiosprint ("Odds Ratios for LIFE1 to URB1")print (np.exp(lreg1.params)) # odd ratios with 95% confidence intervalsprint("COnfiedence Intervals for LIFE1 to URB1")params = lreg1.paramsconf = lreg1.conf_int()conf['OR'] = paramsconf.columns = ['Lower CI', 'Upper CI', 'OR']print (np.exp(conf))###LREG2lreg2 = smf.logit(formula = 'LIFE1 ~ HIV1', data = sub1).fit()print (lreg2.summary()) # odds ratiosprint ("Odds Ratios for LIFE1 to HIV1")print (np.exp(lreg2.params)) # odd ratios with 95% confidence intervalsprint("COnfiedence Intervals for LIFE1 to HIV1")params2 = lreg2.paramsconf2 = lreg2.conf_int()conf2['OR'] = params2conf2.columns = ['Lower CI', 'Upper CI', 'OR']print (np.exp(conf2)) #LREG3lreg3 = smf.logit(formula = 'LIFE1 ~ ALCO1', data = sub1).fit()print (lreg3.summary()) # odds ratiosprint ("Odds Ratios for LIFE1 to ALCO1")print (np.exp(lreg3.params)) # odd ratios with 95% confidence intervalsprint("COnfiedence Intervals for LIFE1 to ALCO1")params3 = lreg3.paramsconf3 = lreg3.conf_int()conf3['OR'] = params3conf3.columns = ['Lower CI', 'Upper CI', 'OR']print (np.exp(conf3)) #LREG4lreg4 = smf.logit(formula = 'LIFE1 ~ INC1', data = sub1).fit()print (lreg4.summary()) # odds ratiosprint ("Odds Ratios for LIFE1 to INC1")print (np.exp(lreg4.params)) # odd ratios with 95% confidence intervalsprint("COnfiedence Intervals for LIFE1 to INC1")params4 = lreg4.paramsconf4 = lreg4.conf_int()conf4 ['OR'] = params4conf4.columns = ['Lower CI', 'Upper CI', 'OR']print (np.exp(conf4))####### Logistic Regression for multiple variables against Life Expectancy##lreg5 = smf.logit(formula = 'LIFE1 ~ URB1 + ALCO1 + HIV1', data = sub1).fit()print (lreg5.summary()) # odd ratios with 95% confidence intervalsparams5 = lreg5.paramsconf5 = lreg5.conf_int()conf5 ['OR'] = params5conf5.columns = ['Lower CI', 'Upper CI', 'OR']print (np.exp(conf5))

0 notes

saltysockmonkey · 4 years ago

Text

Multiple Regression Modeling

For this assignment I used the Gap Minder data set. The hypothesis question is-Is there an association between life expectancy and urban rate.

Upfront, the analysis shows that there is an association between life expectancy and urban rate(P Value=n=1.07e-18) , but there is several lurking variables that need to be found to have a high level of confidence in the model. This was discovered as the R Squared value increases, from 36% to 53%, as I add explanatory variables into the regression model. The diagnostic tests that were run also show that the model is a good fit, but additional variables need to be added to create a better fit.

The response variable for this analysis is lifeexpectancy. The explanatory variables are urbanrate, breastcancerper100th, and incomeperperson.

The first scatter plot displays a positive trend association between life expectancy and urban rate. The output is below. The P Value is below the target, n=1.07e-18, and shows a significant statistical association. But, the R squared value is very low, n=36%, and highlights that 99% of the variability is not being captured by urban rate and there must be confounding variables that are accounted for to gain confidence in my regression model.

At this point, I added 2 other explanatory variables-incomeperperson and breastcancerper100th. The regression output is below with the added explanatory variables that have been centered to the variable's mean. This regression shows a combined P Value well below tolerance, n=1.41e-25, and the R squared value has increased to 53%. The coef values show that the variables have been centered and stabilized at near zero for the regression. The explanatory variables maintain a significant P Value below 0.05 except for Urban Rate's second order polynomial. The second order polynomial regression plot is below and highlights that the model fits because there is a significant P Value(n=0.175) and coef is n= -0.0014 and this highlights that there is no significant association with the quadratic term.

Next, I ran the diagnostic evaluations for the regression model. First was the Q-Q Plot. This plot shows that most of the values follow the trend line, but there is several places where urban rate is below or above the trend line suggesting a curvilinear association that needs additional explanatory variables to discover.

The next diagnostic test was comparing the residuals with standard deviation from the mean. The scatter plot shows the standard deviation of the values. Based on this plot, I can say that because all of the observations fall within 2 standard deviations from the mean. We can account for 95% of the observation variables and this means that the model is a good fit.

The final diagnostic analysis is the influence plot. This plot shows that there are only a few outlier values(+2/-2) and they have a low leverage (<.025). This means that these values have low influence on the regression model's estimation.

OUTPUTLinear Regression with Urban Rate CenteredOLS Regression Results==============================================================================Dep. Variable: lifeexpectancy R-squared: 0.410Model: OLS Adj. R-squared: 0.407Method: Least Squares F-statistic: 118.1Date: Sun, 04 Oct 2020 Prob (F-statistic): 3.15e-21Time: 12:27:49 Log-Likelihood: -593.21No. Observations: 172 AIC: 1190.Df Residuals: 170 BIC: 1197.Df Model: 1Covariance Type: nonrobust===============================================================================coef std err t P>|t| [0.025 0.975]-------------------------------------------------------------------------------Intercept 69.2019 0.584 118.509 0.000 68.049 70.355urbanrate_c 0.2760 0.025 10.869 0.000 0.226 0.326==============================================================================Omnibus: 9.852 Durbin-Watson: 1.932Prob(Omnibus): 0.007 Jarque-Bera (JB): 10.570Skew: -0.604 Prob(JB): 0.00507Kurtosis: 2.866 Cond. No. 23.0============================================================================== Warnings:[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.Polynomial Regression AnalysisOLS Regression Results==============================================================================Dep. Variable: lifeexpectancy R-squared: 0.410Model: OLS Adj. R-squared: 0.403Method: Least Squares F-statistic: 58.72Date: Sun, 04 Oct 2020 Prob (F-statistic): 4.33e-20Time: 12:27:49 Log-Likelihood: -593.21No. Observations: 172 AIC: 1192.Df Residuals: 169 BIC: 1202.Df Model: 2Covariance Type: nonrobust=======================================================================================coef std err t P>|t| [0.025 0.975]---------------------------------------------------------------------------------------Intercept 69.2321 0.825 83.935 0.000 67.604 70.860urbanrate_c 0.2759 0.026 10.792 0.000 0.225 0.326I(urbanrate_c ** 2) -5.704e-05 0.001 -0.052 0.959 -0.002 0.002==============================================================================Omnibus: 9.893 Durbin-Watson: 1.932Prob(Omnibus): 0.007 Jarque-Bera (JB): 10.614Skew: -0.605 Prob(JB): 0.00496Kurtosis: 2.874 Cond. No. 1.06e+03============================================================================== Warnings:[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.[2] The condition number is large, 1.06e+03. This might indicate that there arestrong multicollinearity or other numerical problems.Evalute Model FitOLS Regression Results==============================================================================Dep. Variable: lifeexpectancy R-squared: 0.523Model: OLS Adj. R-squared: 0.514Method: Least Squares F-statistic: 61.37Date: Sun, 04 Oct 2020 Prob (F-statistic): 7.61e-27Time: 12:27:49 Log-Likelihood: -574.94No. Observations: 172 AIC: 1158.Df Residuals: 168 BIC: 1170.Df Model: 3Covariance Type: nonrobust==========================================================================================coef std err t P>|t| [0.025 0.975]------------------------------------------------------------------------------------------Intercept 69.7643 0.749 93.179 0.000 68.286 71.242urbanrate_c 0.1720 0.028 6.068 0.000 0.116 0.228I(urbanrate_c ** 2) -0.0011 0.001 -1.060 0.291 -0.003 0.001breastcancerper100th_c 0.1814 0.029 6.305 0.000 0.125 0.238==============================================================================Omnibus: 8.112 Durbin-Watson: 1.919Prob(Omnibus): 0.017 Jarque-Bera (JB): 8.361Skew: -0.540 Prob(JB): 0.0153Kurtosis: 2.985 Cond. No. 1.07e+03============================================================================== Warnings:[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.[2] The condition number is large, 1.07e+03. This might indicate that there arestrong multicollinearity or other numerical problems.[<matplotlib.lines.Line2D object at 0x7ff8a8445c88>]Figure(432x288)Code import numpy as npimport pandas as pdimport statsmodels.api as statsimport statsmodels.formula.api as smfimport seaborn as sbimport statsmodels.api as smimport matplotlib.pyplot as plt # bug fix for display formats to avoid run time errorspd.set_option('display.float_format', lambda x:'%.2f'%x) #call in data setdata = pd.read_csv('gapminder.csv') # convert variables to numeric format using convert_objects functiondata['incomeperperson'] = pd.to_numeric(data['incomeperperson'], errors='coerce')data['lifeexpectancy'] = pd.to_numeric(data['lifeexpectancy'], errors='coerce')data['urbanrate'] = pd.to_numeric(data['urbanrate'], errors='coerce')data['breastcancerper100th'] = pd.to_numeric(data['breastcancerper100th'], errors='coerce') # Multiple REGRESSION # listwise deletion of missing valuessub1 = data[['urbanrate', 'lifeexpectancy', 'breastcancerper100th', 'co2emissions']].dropna() # first order (linear) scatterplotscat1 = sb.regplot(x='urbanrate', y='lifeexpectancy', scatter=True, data=sub1)plt.xlabel("Urban Rate")plt.ylabel("Life Expectancy") # fit second order polynomial# run the 2 scatterplots together to get both linear and second order fit linesscat1 = sb.regplot(x='urbanrate', y='lifeexpectancy', scatter=True, order=2, data=sub1)plt.xlabel("Urban Rate")plt.ylabel("Life Expectancy") # center quantitative IVs for regression analysissub1['urbanrate_c'] = (sub1['urbanrate'] - sub1['urbanrate'].mean())sub1['breastcancerper100th_c'] = (sub1['breastcancerper100th'] - sub1['breastcancerper100th'].mean())sub1[["breastcancerper100th_c", "urbanrate_c"]].describe() # linear regression analysisprint("Linear Regression with Urban Rate Centered")reg1 = smf.ols('lifeexpectancy ~ urbanrate_c', data=sub1).fit()print (reg1.summary()) # quadratic (polynomial) regression analysis # run following line of code if you get PatsyError 'ImaginaryUnit' object is not callable#del Iprint("Polynomial Regression Analysis")reg2 = smf.ols('lifeexpectancy ~ urbanrate_c + I(urbanrate_c**2)', data=sub1).fit()print (reg2.summary()) ############################## Model Fit Testing###########################print("Evalute Model Fit")reg3 = smf.ols('lifeexpectancy ~ urbanrate_c + I(urbanrate_c**2) + breastcancerper100th_c', data=sub1).fit()print (reg3.summary()) ## Q-Q Testingfig4=sm.qqplot(reg3.resid, line='r') ## Standard residuals ##stdres=pd.DataFrame(reg3.resid_pearson)fig5=plt.plot(stdres, 'o', ls='none')l=plt.axhline(y=0, color='r')plt.ylabel("Life Expectancy")plt.xlabel(" Urban Rate")print(fig5) ## Influence Plot ###fig3=sm.graphics.influence_plot(reg3, size=8)print(fig3)

0 notes

saltysockmonkey · 4 years ago

Text

Basic Linear Regression

For this week’s assignment is used the Gap Minder data set with lifeexpectancy as the response variable(Y) and incomeperperson as the explanatory variable(X). The data set contains quantitative variables and so there is no need to recode the variable values.

The regression model output shows that there is 174 observations for the data set.

The P Value is very low (1.07e-18) and this tells us that there is a significant relationship between the two variables. The R Value(0.362) shows a positive trend, even though it is not strong.

The model’s coef values are identified (65.59 and 0.0006) and can be used to build a best line of fit formula.

--------------------------------------------------------------------------------------------

OUTPUT

------------------------------------------------------------------------------------------

CODE

import numpy as np

import pandas as pd

import statsmodels.api as stats

import statsmodels.formula.api as smf

import seaborn as sb

# bug fix for display formats to avoid run time errors

pd.set_option('display.float_format', lambda x:'%.2f'%x)

#call in data set

data = pd.read_csv('gapminder.csv')

# convert variables to numeric format using convert_objects function

data['incomeperperson'] = pd.to_numeric(data['incomeperperson'], errors='coerce')

data['lifeexpectancy'] = pd.to_numeric(data['lifeexpectancy'], errors='coerce')

############################################################################################

# BASIC LINEAR REGRESSION

############################################################################################

scat1 = sb.regplot(x='incomeperperson', y='lifeexpectancy', scatter=True, data=data)

print(scat1)

print ("OLS regression model for the association between urban rate and internet use rate")

reg1 = smf.ols('lifeexpectancy ~ incomeperperson', data=data).fit()

print (reg1.summary())

0 notes

saltysockmonkey · 4 years ago

Text

Data Set Write Up

Sample The data frames that I used from the Gap Minder dataset include income per person, life expectancy, and urban rate. Gapminder collects data from 213 countries/observations. The data used for life expectancy is collected from IHME and projected populations are based on the UN forecasts from World Population Prospects 2019. Income per person The last variable is urban rate and is aggregated from the World Bank population estimates and the UN World Urbanization Prospects ratios.

Procedures Gapminder was created to inform people about various information points in countries around the world through conducting surveys and data aggregation. Gapminder collects data through random sampling via surveys, financial bank sources, UN population indexes, census polls, and other sources. The Gapminder data is collected across 100 sources and the period of collection is 1970 to 2017 from the Institute for Health Metrics and Evaluation (IMHE). Gapminder also used data from the Global Health Data Exchange for annual estimates. The IHME has data for almost all countries and years between 1970 to 2017. The UN sources has data between 1950 and 2019 while projecting to 2099. Measures

The Gap Minder data set entirely uses quantitative values for all the variables. The data set is available at gapminder.org. Since all the variables are quantitative, if there was any catgorical analysis that needed completed, the def function had to be applied in order to create categorical variables. Life expectancy was the explanatory response. The measure of life expectancy is measured by the average number of years a newborn child would live if the current mortality rates remained unchanged. For analysis life expectancy was binned into 4 groups based on quartiles. The income per person was the response It variable utilizes data from the World Bank and is measured according to the GDP per capita data of a country. Income per person was also binned into 4 groups. Urban rate is measured by the percentage of people living in urban areas. This variable was used as a moderator variable later and had to binned and grouped into 4 categories based on quartile splits.

0 notes

saltysockmonkey · 4 years ago

Text

Data Tools Week 4

For this assignment, I placed the summary up front and the added the code with out output after to simplify the reading due to the amount of code used. I am using the Gap Minder data set. The explanatory variable is incomeperperson and the response variable is lifeepextancy.

For this assignment, the moderator variable is set as urbanrate.

For all of the tests, the data was grouped based on income. Group 1=low income ; Group 2=medium income ; Group 3=middle income ; Group 4=high income.

Data management tasks included converting values to numeric, making blank entries NAN, dropping NAN, and creating functions to group data according to urban rate, income per person, and life expectancy.

For the ANOVA Test, I needed to create a categorical variable for the initial test. I generated 4 categorical groups using the incomeperperson qualitative variable by creating a new function. Once the intial ANOVA was run, I created the moderator variable using urbanrate and created 4 sub groups for urban rates. I then ran the ANOVA Test against the original subgroup and the new urban rate group

The ANOVA was run and shows that there is no statistical significance, P-Values greater than .05, with groups 1,2, and 4-in relationship to the explanatory and response variables with the moderator variable. Group 3 has a significant P Value when comparing urbanrate against incomeperperson and lifeexpectancy. So ANOVA shows that group 3's explanatory and response variables have a relationship with the moderator variable.

For the Chi Test I created 2 categorical variables from incomeperperson and lifeexpectancy from the dataset. Then the Chi Test was run against these 2 variables. Next I generated the moderator variable using urbanrate. Once urbanrate was broken into 4 groups, I ran the Chi Test with the original variables and the each new subgroup for urbanrate.

The Chi Test's output shows that when the moderator variable is added into the test, Groups 3 & 4 generate a P-Value lower than .05, highlighting a significant relationship with the urbanrate variable. A bar graph also displays that there is a positive relationship trend when the variables are compared and tested.

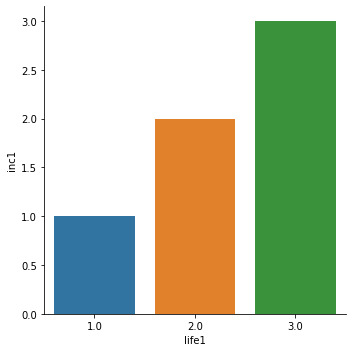
There was minimal data management tasks needed for the last test since the dataset is made up of all quantitative variables. The urbanrate variable was broken into 4 groups and the Pearson test was run against the original dataframe and each new urbanrate subgroup. The Person Correlation test is the final test for this assignment. For this test, the variables remained the same as the previous 2 tests.

The correlation test shows that the group 1 has weak relationships due to the low r-value(.039) and p-value (.08). The other 3 groups generate r-values and p-values that show a strengthening relationship as urban rate and income rate increases. The r-value increases with each group and shows a stronger relationship while the p-value remains below .05 and indicates a significant relationship. The below scatter plot shows the variables plotted and sorted by color. The green and red dots represent groups 3 & 4.

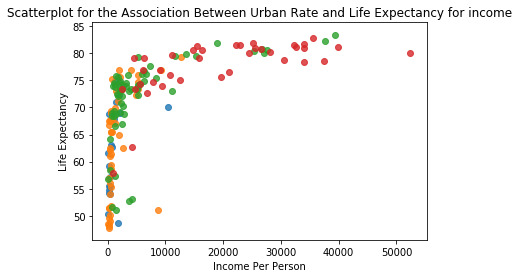
To summarize, each test refined and straightened the hypothesis that urban rate has a relationship with life expectancy and income per person. In the case of ANOVA, I can accept the Alternate Hypothesis that there is a relationship between the variables. The Chi Test continues to support the alternate hypothesis by showing that groups 3 and 4 have a low Outputs ANOVA Outputincome rate levels OLS Regression Results ==============================================================================Dep. Variable: lifeexpectancy R-squared: 0.314Model: OLS Adj. R-squared: 0.306Method: Least Squares F-statistic: 39.67Date: Wed, 09 Sep 2020 Prob (F-statistic): 6.59e-15Time: 10:54:10 Log-Likelihood: -616.44No. Observations: 176 AIC: 1239.Df Residuals: 173 BIC: 1248.Df Model: 2 Covariance Type: nonrobust ================================================================================== coef std err t P>|t| [0.025 0.975]----------------------------------------------------------------------------------Intercept 66.7201 0.695 96.031 0.000 65.349 68.091C(inc1)[T.2.0] 11.7342 1.940 6.047 0.000 7.904 15.564C(inc1)[T.3.0] 14.0902 1.940 7.261 0.000 10.260 17.920==============================================================================Omnibus: 16.013 Durbin-Watson: 1.955Prob(Omnibus): 0.000 Jarque-Bera (JB): 18.340Skew: -0.775 Prob(JB): 0.000104Kurtosis: 2.689 Cond. No. 3.47============================================================================== Warnings:[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.means for Life Expectancy by Income Level lifeexpectancy incomeperperson urbanrateinc1 1.0 66.720147 2351.783373 48.6745592.0 78.454300 15911.876831 75.6450003.0 80.810350 32577.507070 82.352000standard deviation for life expectancy by income level lifeexpectancy incomeperperson urbanrateinc1 1.0 9.082408 2321.563488 20.2330892.0 3.148828 4368.956577 19.8172603.0 1.313176 6725.720440 12.141864urban rate levelsassociation between Life Expectancy and and Income Per Person for Urban Group 1 Low OLS Regression Results ==============================================================================Dep. Variable: lifeexpectancy R-squared: 0.053Model: OLS Adj. R-squared: 0.000Method: Least Squares F-statistic: 1.000Date: Wed, 09 Sep 2020 Prob (F-statistic): 0.331Time: 10:54:10 Log-Likelihood: -69.311No. Observations: 20 AIC: 142.6Df Residuals: 18 BIC: 144.6Df Model: 1 Covariance Type: nonrobust ================================================================================== coef std err t P>|t| [0.025 0.975]----------------------------------------------------------------------------------Intercept 61.7514 1.872 32.985 0.000 57.818 65.685C(inc1)[T.2.0] 8.3726 8.372 1.000 0.331 -9.217 25.962==============================================================================Omnibus: 3.105 Durbin-Watson: 2.341Prob(Omnibus): 0.212 Jarque-Bera (JB): 1.272Skew: 0.100 Prob(JB): 0.529Kurtosis: 1.781 Cond. No. 4.60============================================================================== Warnings:[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.association between Life Expectancy and and Income Per Person for Urban Group 2 Medium OLS Regression Results ==============================================================================Dep. Variable: lifeexpectancy R-squared: 0.053Model: OLS Adj. R-squared: 0.034Method: Least Squares F-statistic: 2.785Date: Wed, 09 Sep 2020 Prob (F-statistic): 0.101Time: 10:54:11 Log-Likelihood: -190.40No. Observations: 52 AIC: 384.8Df Residuals: 50 BIC: 388.7Df Model: 1 Covariance Type: nonrobust ================================================================================== coef std err t P>|t| [0.025 0.975]----------------------------------------------------------------------------------Intercept 63.1583 1.345 46.966 0.000 60.457 65.859C(inc1)[T.2.0] 16.1827 9.697 1.669 0.101 -3.295 35.660==============================================================================Omnibus: 15.846 Durbin-Watson: 1.985Prob(Omnibus): 0.000 Jarque-Bera (JB): 3.826Skew: -0.224 Prob(JB): 0.148Kurtosis: 1.749 Cond. No. 7.28============================================================================== Warnings:[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.association between Life Expectancy and and Income Per Person for Urban Group 3 Middle OLS Regression Results ==============================================================================Dep. Variable: lifeexpectancy R-squared: 0.258Model: OLS Adj. R-squared: 0.235Method: Least Squares F-statistic: 10.98Date: Wed, 09 Sep 2020 Prob (F-statistic): 8.12e-05Time: 10:54:11 Log-Likelihood: -214.90No. Observations: 66 AIC: 435.8Df Residuals: 63 BIC: 442.4Df Model: 2 Covariance Type: nonrobust ================================================================================== coef std err t P>|t| [0.025 0.975]----------------------------------------------------------------------------------Intercept 70.4463 0.875 80.551 0.000 68.699 72.194C(inc1)[T.2.0] 8.1936 2.766 2.963 0.004 2.667 13.720C(inc1)[T.3.0] 10.8094 2.766 3.909 0.000 5.283 16.336==============================================================================Omnibus: 29.947 Durbin-Watson: 2.301Prob(Omnibus): 0.000 Jarque-Bera (JB): 49.457Skew: -1.731 Prob(JB): 1.82e-11Kurtosis: 5.448 Cond. No. 3.73============================================================================== Warnings:[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.association between Life Expectancy and and Income Per Person for Urban Group 4 High OLS Regression Results ==============================================================================Dep. Variable: lifeexpectancy R-squared: 0.053Model: OLS Adj. R-squared: 0.000Method: Least Squares F-statistic: 1.000Date: Wed, 09 Sep 2020 Prob (F-statistic): 0.331Time: 10:54:11 Log-Likelihood: -69.311No. Observations: 20 AIC: 142.6Df Residuals: 18 BIC: 144.6Df Model: 1 Covariance Type: nonrobust ================================================================================== coef std err t P>|t| [0.025 0.975]----------------------------------------------------------------------------------Intercept 61.7514 1.872 32.985 0.000 57.818 65.685C(inc1)[T.2.0] 8.3726 8.372 1.000 0.331 -9.217 25.962==============================================================================Omnibus: 3.105 Durbin-Watson: 2.341Prob(Omnibus): 0.212 Jarque-Bera (JB): 1.272Skew: 0.100 Prob(JB): 0.529Kurtosis: 1.781 Cond. No. 4.60============================================================================== Warnings:[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.means for Life Expectancy by Income Per Person for Urban Group 1 lifeexpectancy incomeperperson urbanrate inc1urb1 1.0 62.17 1304.690529 18.679 1.05means for Life Expectancy by Income Per Person for Urban Group 2 lifeexpectancy incomeperperson urbanrate inc1urb1 2.0 63.469481 1764.840618 37.084615 1.019231means for Life Expectancy by Income Per Person for Urban Group 3 lifeexpectancy incomeperperson urbanrate inc1urb1 3.0 72.173803 6497.448498 63.328485 1.272727means for Life Expectancy by Income Per Person for Urban Group 4 lifeexpectancy incomeperperson urbanrate inc1urb1 4.0 77.682868 19550.870875 86.79 2.052632 Chi Test OutputStandard Deviation for Life Expectancycount 191.000000mean 69.753524std 9.708621min 47.79400025% 64.44700050% 73.13100075% 76.593000max 83.394000Name: lifeexpectancy, dtype: float64Standard Deviation for Income Per Personcount 190.000000mean 8740.966076std 14262.809083min 103.77585725% 748.24515150% 2553.49605675% 9379.891165max 105147.437697Name: incomeperperson, dtype: float64Chi Square Analysis for Explanatory and Response VariablesC:\Users\sockm\anaconda3\lib\site-packages\seaborn\categorical.py:3669: UserWarning: The `factorplot` function has been renamed to `catplot`. The original name will be removed in a future release. Please update your code. Note that the default `kind` in `factorplot` (`'point'`) has changed `'strip'` in `catplot`. warnings.warn(msg)inc1 1.0 2.0 3.0life1 1.0 136 0 02.0 0 20 03.0 0 0 20inc1 1.0 2.0 3.0life1 1.0 1.0 0.0 0.02.0 0.0 1.0 0.03.0 0.0 0.0 1.0chi-square value, p value, expected counts(351.99999999999994, 6.488502127788041e-75, 4, array([[105.09090909, 15.45454545, 15.45454545], [ 15.45454545, 2.27272727, 2.27272727], [ 15.45454545, 2.27272727, 2.27272727]]))Adding Moderator Variableinc1 1.0 2.0life1 1.0 19 02.0 0 1inc1 1.0 2.0 3.0life1 1.0 0.139706 0.00 NaN2.0 0.000000 0.05 NaNchi-square value, p value, expected counts(4.487534626038781, 0.03414288228006565, 1, array([[18.05, 0.95], [ 0.95, 0.05]]))inc1 1.0 2.0life1 1.0 51 02.0 0 1inc1 1.0 2.0 3.0life1 1.0 0.375 0.00 NaN2.0 0.000 0.05 NaNchi-square value, p value, expected counts(12.49519415609381, 0.00040800022640174056, 1, array([[5.00192308e+01, 9.80769231e-01], [9.80769231e-01, 1.92307692e-02]]))inc1 1.0 2.0 3.0life1 1.0 54 0 02.0 0 6 03.0 0 0 6inc1 1.0 2.0 3.0life1 1.0 0.397059 0.0 0.02.0 0.000000 0.3 0.03.0 0.000000 0.0 0.3chi-square value, p value, expected counts(132.00000000000003, 1.4542497475734214e-27, 4, array([[44.18181818, 4.90909091, 4.90909091], [ 4.90909091, 0.54545455, 0.54545455], [ 4.90909091, 0.54545455, 0.54545455]]))inc1 1.0 2.0 3.0life1 1.0 12 0 02.0 0 12 03.0 0 0 14inc1 1.0 2.0 3.0life1 1.0 0.088235 0.0 0.02.0 0.000000 0.6 0.03.0 0.000000 0.0 0.7chi-square value, p value, expected counts(76.0, 1.2242617888987312e-15, 4, array([[3.78947368, 3.78947368, 4.42105263], [3.78947368, 3.78947368, 4.42105263], [4.42105263, 4.42105263, 5.15789474]])) Pearson Correlation Output urban rate levelsassociation between urbanrate and life expecatany for LOW income countries(0.39070589367158226, 0.08852079337577021) association between urbanrate and life expecatany for Medium income countries(0.4750165695713443, 0.0004908618152919306) association between urbanrate and life expecatany for Middle income countries(0.5530182478009116, 2.600193675208846e-06) association between urbanrate and life expecatany for High income countries(0.6062786995430565, 5.474886254266103e-05) AxesSubplot(0.125,0.125;0.775x0.755)AxesSubplot(0.125,0.125;0.775x0.755)AxesSubplot(0.125,0.125;0.775x0.755)AxesSubplot(0.125,0.125;0.775x0.755) ANOVA Code# ANOVA import numpy as npimport pandas as pdimport statsmodels.formula.api as smfimport statsmodels.stats.multicomp as multiimport seabornimport matplotlib.pyplot as plt data = pd.read_csv('gapminder.csv', low_memory=False) #Convert Blank to NAN and numeric conversiondata['incomeperperson']=data.incomeperperson.replace(" " ,np.nan)data['incomeperperson'] = pd.to_numeric(data.incomeperperson) data['lifeexpectancy']=data.lifeexpectancy.replace(" " ,np.nan)data['lifeexpectancy'] = pd.to_numeric(data.lifeexpectancy) data['urbanrate'] = data.urbanrate.replace(" ",np.nan)data['urbanrate'] = pd.to_numeric(data.urbanrate) # subset variables in new data frame, sub1sub1=data[['lifeexpectancy', 'incomeperperson', 'urbanrate']].dropna() #assign variables to sub4 #Standard Deviationsprint ("standard deviation for life expectancy by income level")st1= data['lifeexpectancy'].std()print (st1) ## Income Levelsdef INCOMERATE(row): if row['incomeperperson'] < 10000: return 1 if row['incomeperperson'] >10000 and row['incomeperperson'] <=25000: return 2 if row['incomeperperson'] >25000 and row['incomeperperson'] <=100000: return 3 if row['incomeperperson'] >100000: return 4 #incomerate function appliedprint ("income rate levels")sub2=sub1sub2['inc1'] = INCOMERATEsub2['inc1'] = data.apply (lambda row: INCOMERATE (row),axis=1) #b = sub2['inc1'].head (n=50)#print(b) #Initial ANOVA with Means and STD DEV model1 = smf.ols(formula='lifeexpectancy ~ C(inc1)', data=sub2).fit()print (model1.summary()) print ("means for Life Expectancy by Income Level")m1= sub2.groupby('inc1').mean()print (m1) print ("standard deviation for life expectancy by income level")st1= sub2.groupby('inc1').std()print (st1) ## Urban Rate Levelsdef URBANRATE(row): if row['urbanrate'] < 25: return 1 if row['urbanrate'] >25 and row['urbanrate'] <=50: return 2 if row['urbanrate'] >50 and row['urbanrate'] <=75: return 3 if row['urbanrate'] >75: return 4 print ("urban rate levels")sub2=sub1sub2['urb1'] = URBANRATEsub2['urb1'] = data.apply (lambda row: URBANRATE (row),axis=1) ##Moderator Levelssub3=sub2[(sub2['urb1']== 1)]sub4=sub2[(sub2['urb1']== 2)]sub5=sub2[(sub2['urb1']== 3)]sub6=sub2[(sub2['urb1']== 4)] #Moderation ANOVA URB1print ('association between Life Expectancy and and Income Per Person for Urban Group 1')model2 = smf.ols(formula='lifeexpectancy ~ C(inc1)', data=sub3).fit()print (model2.summary()) print ('association between Life Expectancy and and Income Per Person for Urban Group 2')model3 = smf.ols(formula='lifeexpectancy ~ C(inc1)', data=sub4).fit()print (model3.summary()) print ('association between Life Expectancy and and Income Per Person for Urban Group 3')model4 = smf.ols(formula='lifeexpectancy ~ C(inc1)', data=sub5).fit()print (model4.summary()) print ('association between Life Expectancy and and Income Per Person for Urban Group 4')model5 = smf.ols(formula='lifeexpectancy ~ C(inc1)', data=sub3).fit()print (model5.summary()) ## Meansprint ("means for Life Expectancy by Income Per Person for Urban Group 1")m1= sub3.groupby('urb1').mean()print (m1) print ("means for Life Expectancy by Income Per Person for Urban Group 2")m2= sub4.groupby('urb1').mean()print (m2) print ("means for Life Expectancy by Income Per Person for Urban Group 3")m3= sub5.groupby('urb1').mean()print (m3) print ("means for Life Expectancy by Income Per Person for Urban Group 4")m4= sub6.groupby('urb1').mean()print (m4)## End ANOVA Chi Test Code# Chi Square import numpy as npimport pandas as pdimport statsmodels.formula.api as smfimport statsmodels.stats.multicomp as multiimport seaborn as sbimport matplotlib.pyplot as pltimport scipy.stats as stats data = pd.read_csv('gapminder.csv', low_memory=False) #Convert Blank to NAN and numeric conversiondata['incomeperperson']=data.incomeperperson.replace(" " ,np.nan)data['incomeperperson'] = pd.to_numeric(data.incomeperperson) data['lifeexpectancy']=data.lifeexpectancy.replace(" " ,np.nan)data['lifeexpectancy'] = pd.to_numeric(data.lifeexpectancy) data['urbanrate'] = data.urbanrate.replace(" ",np.nan)data['urbanrate'] = pd.to_numeric(data.urbanrate) #Standard deviationsprint("Standard Deviation for Life Expectancy")dev1=data.lifeexpectancy.describe()print(dev1) print("Standard Deviation for Income Per Person")dev2=data.incomeperperson.describe()print(dev2) # subset variables in new data frame, sub1sub1=data[['lifeexpectancy', 'incomeperperson', 'urbanrate']].dropna() #assign variables to sub4 ## Income Levelsdef INCOMERATE(row): if row['incomeperperson'] < 10000: return 1 if row['incomeperperson'] >10000 and row['incomeperperson'] <=25000: return 2 if row['incomeperperson'] >25000 and row['incomeperperson'] <=100000: return 3 if row['incomeperperson'] >100000: return 4 #incomerate function applied#print ("income rate levels")sub2=sub1sub2['inc1'] = INCOMERATEsub2['inc1'] = data.apply (lambda row: INCOMERATE (row),axis=1) #Life Expectancy Levelsdef LIFEEXPECT(row): if row['lifeexpectancy'] < 55: return 1 if row['lifeexpectancy'] >55 and row['incomeperperson'] <=65: return 2 if row['lifeexpectancy'] >65 and row['incomeperperson'] <=75: return 3 if row['lifeexpectancy'] >75: return 4 #life expectancy function appliedsub2=sub1sub2['life1'] = INCOMERATEsub2['life1'] = data.apply (lambda row: INCOMERATE (row),axis=1) #Initial Chi Square with Means and STD DEVprint("Chi Square Analysis for Explanatory and Response Variables") # Bar Graph plot for first bivariatessb.factorplot(x="life1", y="inc1", data=sub2, kind="bar", ci=None)plt.xlabel=("Life Expectancy Rate")plt.ylabel=("Income Rate") # chi-square for first two variable# contingency table of observed countsct1=pd.crosstab(sub2['life1'], sub2['inc1'])print (ct1) # column percentagescolsum=ct1.sum(axis=0)colpct=ct1/colsumprint(colpct) # chi-squareprint ('chi-square value, p value, expected counts')cs1= stats.chi2_contingency(ct1)print (cs1) # Moderator areaprint("Adding Moderator Variable")## Urban Rate Levelsdef URBANRATE(row): if row['urbanrate'] < 25: return 1 if row['urbanrate'] >25 and row['urbanrate'] <=50: return 2 if row['urbanrate'] >50 and row['urbanrate'] <=75: return 3 if row['urbanrate'] >75: return 4 # URBANRATE Applied#print ("urban rate levels")sub2=sub1sub2['urb1'] = URBANRATEsub2['urb1'] = data.apply (lambda row: URBANRATE (row),axis=1) ##Urban Group Levelssub3=sub2[(sub2['urb1']== 1)]sub4=sub2[(sub2['urb1']== 2)]sub5=sub2[(sub2['urb1']== 3)]sub6=sub2[(sub2['urb1']== 4)] # chi-square with moderator variable added#Moderator Group 1# contingency table of observed countsct2=pd.crosstab(sub3['life1'], sub3['inc1'])print (ct2) # column percentagescolsum2=ct2.sum(axis=0)colpct2=ct2/colsumprint(colpct2) # chi-squareprint ('chi-square value, p value, expected counts')cs2= stats.chi2_contingency(ct2)print (cs2) #Moderator Group 2# contingency table of observed countsct3=pd.crosstab(sub4['life1'], sub4['inc1'])print (ct3) # column percentagescolsum3=ct3.sum(axis=0)colpct3=ct3/colsumprint(colpct3) # chi-squareprint ('chi-square value, p value, expected counts')cs3= stats.chi2_contingency(ct3)print (cs3) #Moderator Group 3# contingency table of observed countsct4=pd.crosstab(sub5['life1'], sub5['inc1'])print (ct4) # column percentagescolsum4=ct4.sum(axis=0)colpct4=ct4/colsumprint(colpct4) # chi-squareprint ('chi-square value, p value, expected counts')cs4= stats.chi2_contingency(ct4)print (cs4) #Moderator Group 4# contingency table of observed countsct5=pd.crosstab(sub6['life1'], sub6['inc1'])print (ct5) # column percentagescolsum5=ct5.sum(axis=0)colpct5=ct5/colsumprint(colpct5) # chi-squareprint ('chi-square value, p value, expected counts')cs5= stats.chi2_contingency(ct5)print (cs5)##End CHI Test Pearson Code @author: sockm"""import pandas as pdimport numpy as npimport seaborn as sbimport scipy.statsimport matplotlib.pyplot as plt gmdata = pd.read_csv('gapminder.csv', low_memory=False) #Convert Blank to NAN and numeric conversiongmdata['urbanrate']=gmdata.urbanrate.replace(" " ,np.nan)gmdata['urbanrate'] = pd.to_numeric(gmdata.urbanrate) gmdata['incomeperperson']=gmdata.incomeperperson.replace(" " ,np.nan)gmdata['incomeperperson'] = pd.to_numeric(gmdata.incomeperperson) gmdata['lifeexpectancy']=gmdata.incomeperperson.replace(" " ,np.nan)gmdata['lifeexpectancy'] = pd.to_numeric(gmdata.incomeperperson) sub1=gmdata[['incomeperperson', 'urbanrate','lifeexpectancy']].dropna()print(sub1) #Scatter Plotsb.regplot(x='incomeperperson', y='lifeexpectancy', fit_reg=False, data=sub1)plt.xlabel("Income Per Person")plt.ylabel("Life Expectancy")#plt.title('Scatterplot for the Association Between Urban Rate and Income Per Person Rate') ## Pearon for first 2 variablesprint ('association between life expectancy and income per person')print (scipy.stats.pearsonr(sub1['lifeexpectancy'], sub1['incomeperperson'])) ##Exp & Resp Variable groupings## Income Levelssub2=sub1 ##Moderdate Variable## Urban Rate Levels to Categoricaldef URBANRATE(row): if row['urbanrate'] < 25: return 1 if row['urbanrate'] >26 and row['urbanrate'] <49: return 2 if row['urbanrate'] >50 and row['urbanrate'] < 74: return 3 if row['urbanrate'] >75: return 4 #urbanrate function appliedprint ("urban rate levels")sub2['urb1'] = URBANRATEsub2['urb1'] = sub1.apply (lambda row: URBANRATE (row),axis=1) #sub3=sub2[['inc1', 'life1', 'urb1']].head (n=50)#print(sub3) sub3=sub2[(sub2['urb1']== 1)]sub4=sub2[(sub2['urb1']== 2)]sub5=sub2[(sub2['urb1']== 3)]sub6=sub2[(sub2['urb1']== 4)] print ('association between urbanrate and life expecatany for LOW income countries')print (scipy.stats.pearsonr(sub3['urbanrate'], sub3['lifeexpectancy']))print (' ')print ('association between urbanrate and life expecatany for Medium income countries')print (scipy.stats.pearsonr(sub4['urbanrate'], sub4['lifeexpectancy']))print (' ')print ('association between urbanrate and life expecatany for Middle income countries')print (scipy.stats.pearsonr(sub5['urbanrate'], sub5['lifeexpectancy']))print (' ')print ('association between urbanrate and life expecatany for High income countries')print (scipy.stats.pearsonr(sub6['urbanrate'], sub6['lifeexpectancy']))print (' ') ## Scatter Plots#%%scat1 = sb.regplot(x='urb1', y='lifeexpectancy', fit_reg=False,data=sub3)plt.xlabel("Urban Rate")plt.ylabel("Life Expectancy")plt.title('Scatterplot for the Association Between Urban Rate and Life Expectancy for LOW income countries')print (scat1)#%%scat2 = sb.regplot(x='urb1', y='lifeexpectancy', fit_reg=False, data=sub4)plt.xlabel("Urban Rate")plt.ylabel("Life Expectancy")plt.title('Scatterplot for the Association Between Urban Rate and Life Expectancy for MIDDLE income countries')print (scat2)#%%scat3 = sb.regplot(x='urb1', y='lifeexpectancy',fit_reg=False, data=sub5)plt.xlabel("Urban Rate")plt.ylabel("Life Expectancy")plt.title('Scatterplot for the Association Between Urban Rate and Life Expectancy for MEDIUM income countries')print (scat3)#%%scat4 = sb.regplot(x='urb1', y='lifeexpectancy',fit_reg=False, data=sub6)plt.xlabel("Urban Rate")plt.ylabel("Life Expectancy")plt.title('Scatterplot for the Association Between Urban Rate and Life Expectancy for HIGH income countries')print (scat4)

0 notes

saltysockmonkey · 4 years ago

Text

Quantitative Correlation

For this assignment I used the variables urbanrate & incomeperperson. First steps was to remove blanks in the dataset and then convert to numeric.

The Scatter Plot for these variables is below. It shows a weak positive relationship between the two variables.

Next I calculated the correlation using the pearsonr function in python. Here is the output:

association between urbanrate and internetuserate (0.49009424225988746, 8.202764568266556e-13)

The r-value of 0.49 validates a weaker positive relationship and the p-value is very minimal and highlights a significant relationship.

The r squared value is 0.2401 and this indicates that we can predict @ 24% of the results,but further analysis is needed since we won’t be able to predict 76% of the results.

Code is below:

import pandas as pd import numpy as np import seaborn as sb import scipy import matplotlib.pyplot as plt

gmdata = pd.read_csv('gapminder.csv', low_memory=False)

#Convert Blank to NAN and numeric conversion gmdata['urbanrate']=gmdata.urbanrate.replace(" " ,np.nan) gmdata['urbanrate'] = pd.to_numeric(gmdata.urbanrate)

gmdata['incomeperperson']=gmdata.incomeperperson.replace(" " ,np.nan) gmdata['incomeperperson'] = pd.to_numeric(gmdata.incomeperperson)

#Scatter Plot sb.regplot(x='urbanrate', y='incomeperperson', fit_reg=True, data=gmdata) plt.xlabel("urbanrate") plt.ylabel("Income Per Person Rate") plt.title('Scatterplot for the Association Between Urban Rate and Income Per Person Rate')

data_clean=gmdata.dropna()

print ('association between urbanrate and internetuserate') print (scipy.stats.pearsonr(data_clean['urbanrate'], data_clean['incomeperperson']))

0 notes

saltysockmonkey · 4 years ago

Text

Chi Test and Pair wise comparison

For Week two’s exercise I used the Gap Minder data set and the hypothesis question is there a relationship between urban rate and income per person.

The two variables are incomeperperson and urbanrate. Urbanrate is the explanatory variable and incomeperperson is the response variable. In the DS, both variables are quantitative.

First steps included calling in the DS, replacing blanks with NAN, converting to numeric, and producing standard deviation outputs for the two variables.

Here is the standard deviation results:

Urban Rate Deviation count 203.000000 mean 56.769360 std 23.844933 min 10.400000 25% 36.830000 50% 57.940000 75% 74.210000 max 100.000000

Name: urbanrate, dtype: float64 Income Per Person Deviation count 190.000000 mean 8740.966076 std 14262.809083 min 103.775857 25% 748.245151 50% 2553.496056 75% 9379.891165 max 105147.437697

Next step is to create levels for each variable to make then categorical. Urbanrate has 4 levels and incomeperperson has 8 levels. Here is the cross tab results:

urban rate levels income rate levels inc2 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0 urb2 1.0 10 2 7 0 0 1 0 1 0 2.0 18 14 11 2 6 2 0 0 0 3.0 3 4 27 7 14 5 6 0 0 4.0 0 1 1 3 8 14 14 2 1 inc2 1.0 2.0 3.0 4.0 ... 6.0 7.0 8.0 9.0 urb2 ... 1.0 0.322581 0.095238 0.152174 0.000000 ... 0.045455 0.0 0.333333 0.0 2.0 0.580645 0.666667 0.239130 0.166667 ... 0.090909 0.0 0.000000 0.0 3.0 0.096774 0.190476 0.586957 0.583333 ... 0.227273 0.3 0.000000 0.0 4.0 0.000000 0.047619 0.021739 0.250000 ... 0.636364 0.7 0.666667 1.0

Then I generate a bar graph that shows that urbanrate groups 3 & 4 are different that groups 1 & 2.

Now I need to determine the Bonferonni Adjustment for the P value. Based on 4 groups the new P Value is 0.0125.

So I create a Chi square test table but it needs to be reduced to be effective.

Now I due a pairwise comparison for groups 3 & 4 against the other groups.

Overall, the P values are below .0125(adjusted P value) and this determines a significant difference in the groups and I can then reject the null hypothesis.

Python Code

-------------------------

# -*- coding: utf-8 -*- """ Created on Wed Aug 19 08:42:13 2020

@author: sockm """ import pandas as pd import numpy as np import seaborn as sb import statsmodels.formula.api as smf import statsmodels.stats.multicomp as multi import scipy.stats as stats import matplotlib.pyplot as plt

# Data Set call in gmdata = pd.read_csv('gapminder.csv', low_memory=False)

#Convert Blank to NAN and numeric conversion sub1=gmdata sub1['urbanrate']=gmdata.urbanrate.replace(" " ,np.nan) sub1['urbanrate'] = pd.to_numeric(gmdata.urbanrate)

sub2=gmdata sub2['incomeperperson']=gmdata.incomeperperson.replace(" " ,np.nan) sub2['incomeperperson'] = pd.to_numeric(gmdata.incomeperperson)

#Standard Deviations print("Urban Rate Deviation") desc1=sub1.urbanrate.describe() print(desc1)

print("Income Per Person Deviation") desc2=sub2.incomeperperson.describe() print(desc2)

#Urban Rate Grouping/Level # subset variables in new data frame, Explanatory Variable sub4=gmdata[['incomeperperson', 'urbanrate']].dropna() #assign variables to sub4

## Urban Rate Levels to Categorical def URBANRATE(row): if row['urbanrate'] < 25: return 1 if row['urbanrate'] >26 and row['urbanrate'] <49: return 2 if row['urbanrate'] >50 and row['urbanrate'] < 74: return 3 if row['urbanrate'] >75: return 4

#urbanrate function applied print ("urban rate levels") sub4['urb2'] = URBANRATE sub4['urb2'] = sub1.apply (lambda row: URBANRATE (row),axis=1)

#Income Levels to Categorical def INCOMERATE(row): if row['incomeperperson'] < 500: return 1 if row['incomeperperson'] >501 and row['incomeperperson'] <1000: return 2 if row['incomeperperson'] >1001 and row['incomeperperson'] < 3000: return 3 if row['incomeperperson'] >3001 and row['incomeperperson'] <5000: return 4 if row['incomeperperson'] >5001 and row['incomeperperson'] <10000: return 5 if row['incomeperperson'] >10001 and row['incomeperperson'] < 25000: return 6 if row['incomeperperson'] >25001 and row['incomeperperson'] <50000: return 7 if row['incomeperperson'] >50001 and row['incomeperperson'] <100000: return 8 if row['incomeperperson'] >100000: return 9

#INCOMERATE function applied Response Variable print ("income rate levels") #sub4 variable call to sub4 sub4['inc2'] = INCOMERATE sub4['inc2'] = sub1.apply (lambda row: INCOMERATE (row),axis=1)

# Bar Graph plot sb.factorplot(x="urb2", y="inc2", data=sub4, kind="bar", ci=None) plt.xlabel=("Urban Rate") plt.ylabel=("Income Rate")

# contingency table of observed counts ct1=pd.crosstab(sub4['urb2'], sub4['inc2']) print (ct1)

# column percentages colsum=ct1.sum(axis=0) colpct=ct1/colsum print(colpct)

# chi-square print ('chi-square value, p value, expected counts FOR ALL') cs1= stats.chi2_contingency(ct1) print (cs1)

#Post Hoc #Pair wise for 1 & 3 recode1 = {1: 1, 3: 3} temp1=sub4 temp1['COMP1v3'] = sub4['urb2'].map(recode1)

# contingency table of observed counts ct1=pd.crosstab(sub4['inc2'], temp1['COMP1v3']) print (ct1)

# column percentages colsum=ct1.sum(axis=0) colpct=ct1/colsum print(colpct)

print ('chi-square value, p value, expected counts for 3 to 1 comparison') cs1= stats.chi2_contingency(ct1) print (cs1)

#Pair wise for 2 & 3 recode2 = {2: 2, 3: 3} temp2=sub4 temp2['COMP2v3'] = sub4['urb2'].map(recode2)

# contingency table of observed counts ct2=pd.crosstab(sub4['inc2'], temp2['COMP2v3']) print (ct2)

# column percentages colsum=ct2.sum(axis=0) colpct=ct2/colsum print(colpct)

print ('chi-square,p value,expected counts for 3 to 2 comparison') cs2= stats.chi2_contingency(ct2) print(cs2)

#Pair wise for 4 & 3 recode3 = {4: 4, 3: 3} temp3=sub4 temp3['COMP4v3'] = sub4['urb2'].map(recode3)

# contingency table of observed counts ct3=pd.crosstab(sub4['inc2'], temp3['COMP4v3']) print (ct3)

# column percentages colsum=ct3.sum(axis=0) colpct=ct3/colsum print(colpct)

print ('chi-square,p value,expected counts for 3 to 4 comparison') cs3= stats.chi2_contingency(ct3) print(cs3)

#Pair wise for 1 & 4 recode4 = {1: 1, 4: 4} temp4=sub4 temp4['COMP1v4'] = sub4['urb2'].map(recode4)

# contingency table of observed counts ct4=pd.crosstab(sub4['inc2'], temp4['COMP1v4']) print (ct4)

# column percentages colsum=ct4.sum(axis=0) colpct=ct4/colsum print(colpct)

print ('chi-square value, p value, expected counts for 4 to 1 comparison') cs4= stats.chi2_contingency(ct4) print (cs4)

#Pair wise for 2 & 4 recode5 = {2: 2, 4: 4} temp5=sub4 temp5['COMP2v4'] = sub4['urb2'].map(recode5)

# contingency table of observed counts ct5=pd.crosstab(sub4['inc2'], temp5['COMP2v4']) print (ct5)

# column percentages colsum=ct5.sum(axis=0) colpct=ct5/colsum print(colpct)

print ('chi-square,p value,expected counts for 4 to 2 comparison') cs5= stats.chi2_contingency(ct5) print(cs5)

#Pair wise for 3 & 4 recode6 = {4: 4, 3: 3} temp6=sub4 temp6['COMP3v4'] = sub4['urb2'].map(recode6)

# contingency table of observed counts ct6=pd.crosstab(sub4['inc2'], temp6['COMP3v4']) print (ct6)

# column percentages colsum=ct6.sum(axis=0) colpct=ct6/colsum print(colpct)

print ('chi-square,p value,expected counts for 4 to 3 comparison') cs6= stats.chi2_contingency(ct6) print(cs6)

----------------------------------------------------------------

Output

Urban Rate Deviation count 203.000000 mean 56.769360 std 23.844933 min 10.400000 25% 36.830000 50% 57.940000 75% 74.210000 max 100.000000 Name: urbanrate, dtype: float64 Income Per Person Deviation count 190.000000 mean 8740.966076 std 14262.809083 min 103.775857 25% 748.245151 50% 2553.496056 75% 9379.891165 max 105147.437697 Name: incomeperperson, dtype: float64 urban rate levels income rate levels inc2 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0 urb2 1.0 10 2 7 0 0 1 0 1 0 2.0 18 14 11 2 6 2 0 0 0 3.0 3 4 27 7 14 5 6 0 0 4.0 0 1 1 3 8 14 14 2 1 inc2 1.0 2.0 3.0 4.0 ... 6.0 7.0 8.0 9.0 urb2 ... 1.0 0.322581 0.095238 0.152174 0.000000 ... 0.045455 0.0 0.333333 0.0 2.0 0.580645 0.666667 0.239130 0.166667 ... 0.090909 0.0 0.000000 0.0 3.0 0.096774 0.190476 0.586957 0.583333 ... 0.227273 0.3 0.000000 0.0 4.0 0.000000 0.047619 0.021739 0.250000 ... 0.636364 0.7 0.666667 1.0

[4 rows x 9 columns] chi-square value, p value, expected counts FOR ALL (129.83783523184445, 1.6598113194807335e-16, 24, array([[ 3.53804348, 2.39673913, 5.25 , 1.36956522, 3.19565217, 2.51086957, 2.2826087 , 0.3423913 , 0.11413043], [ 8.92934783, 6.04891304, 13.25 , 3.45652174, 8.06521739, 6.33695652, 5.76086957, 0.86413043, 0.28804348], [11.11956522, 7.5326087 , 16.5 , 4.30434783, 10.04347826, 7.89130435, 7.17391304, 1.07608696, 0.35869565], [ 7.41304348, 5.02173913, 11. , 2.86956522, 6.69565217, 5.26086957, 4.7826087 , 0.7173913 , 0.23913043]])) COMP1v3 1.0 3.0 inc2 1.0 10 3 2.0 2 4 3.0 7 27 4.0 0 7 5.0 0 14 6.0 1 5 7.0 0 6 8.0 1 0 COMP1v3 1.0 3.0 inc2 1.0 0.476190 0.045455 2.0 0.095238 0.060606 3.0 0.333333 0.409091 4.0 0.000000 0.106061 5.0 0.000000 0.212121 6.0 0.047619 0.075758 7.0 0.000000 0.090909 8.0 0.047619 0.000000 chi-square value, p value, expected counts for 3 to 1 comparison (32.208399443693565, 3.715715191724342e-05, 7, array([[ 3.13793103, 9.86206897], [ 1.44827586, 4.55172414], [ 8.20689655, 25.79310345], [ 1.68965517, 5.31034483], [ 3.37931034, 10.62068966], [ 1.44827586, 4.55172414], [ 1.44827586, 4.55172414], [ 0.24137931, 0.75862069]])) COMP2v3 2.0 3.0 inc2 1.0 18 3 2.0 14 4 3.0 11 27 4.0 2 7 5.0 6 14 6.0 2 5 7.0 0 6 COMP2v3 2.0 3.0 inc2 1.0 0.339623 0.045455 2.0 0.264151 0.060606 3.0 0.207547 0.409091 4.0 0.037736 0.106061 5.0 0.113208 0.212121 6.0 0.037736 0.075758 7.0 0.000000 0.090909 chi-square,p value,expected counts for 3 to 2 comparison (35.27093727744174, 3.8186749006078295e-06, 6, array([[ 9.35294118, 11.64705882], [ 8.01680672, 9.98319328], [16.92436975, 21.07563025], [ 4.00840336, 4.99159664], [ 8.90756303, 11.09243697], [ 3.11764706, 3.88235294], [ 2.67226891, 3.32773109]])) COMP4v3 3.0 4.0 inc2 1.0 3 0 2.0 4 1 3.0 27 1 4.0 7 3 5.0 14 8 6.0 5 14 7.0 6 14 8.0 0 2 9.0 0 1 COMP4v3 3.0 4.0 inc2 1.0 0.045455 0.000000 2.0 0.060606 0.022727 3.0 0.409091 0.022727 4.0 0.106061 0.068182 5.0 0.212121 0.181818 6.0 0.075758 0.318182 7.0 0.090909 0.318182 8.0 0.000000 0.045455 9.0 0.000000 0.022727 chi-square,p value,expected counts for 3 to 4 comparison (39.83581111870586, 3.4373880915658388e-06, 8, array([[ 1.8, 1.2], [ 3. , 2. ], [16.8, 11.2], [ 6. , 4. ], [13.2, 8.8], [11.4, 7.6], [12. , 8. ], [ 1.2, 0.8], [ 0.6, 0.4]])) COMP1v4 1.0 4.0 inc2 1.0 10 0 2.0 2 1 3.0 7 1 4.0 0 3 5.0 0 8 6.0 1 14 7.0 0 14 8.0 1 2 9.0 0 1 COMP1v4 1.0 4.0 inc2 1.0 0.476190 0.000000 2.0 0.095238 0.022727 3.0 0.333333 0.022727 4.0 0.000000 0.068182 5.0 0.000000 0.181818 6.0 0.047619 0.318182 7.0 0.000000 0.318182 8.0 0.047619 0.045455 9.0 0.000000 0.022727 chi-square value, p value, expected counts for 4 to 1 comparison (50.63469516594517, 3.085426962262538e-08, 8, array([[ 3.23076923, 6.76923077], [ 0.96923077, 2.03076923], [ 2.58461538, 5.41538462], [ 0.96923077, 2.03076923], [ 2.58461538, 5.41538462], [ 4.84615385, 10.15384615], [ 4.52307692, 9.47692308], [ 0.96923077, 2.03076923], [ 0.32307692, 0.67692308]])) C:\Users\sockm\anaconda3\lib\site-packages\seaborn\categorical.py:3669: UserWarning: The `factorplot` function has been renamed to `catplot`. The original name will be removed in a future release. Please update your code. Note that the default `kind` in `factorplot` (`'point'`) has changed `'strip'` in `catplot`. warnings.warn(msg) COMP2v4 2.0 4.0 inc2 1.0 18 0 2.0 14 1 3.0 11 1 4.0 2 3 5.0 6 8 6.0 2 14 7.0 0 14 8.0 0 2 9.0 0 1 COMP2v4 2.0 4.0 inc2 1.0 0.339623 0.000000 2.0 0.264151 0.022727 3.0 0.207547 0.022727 4.0 0.037736 0.068182 5.0 0.113208 0.181818 6.0 0.037736 0.318182 7.0 0.000000 0.318182 8.0 0.000000 0.045455 9.0 0.000000 0.022727 chi-square,p value,expected counts for 4 to 2 comparison (63.79990198480764, 8.330827897764254e-11, 8, array([[9.83505155, 8.16494845], [8.19587629, 6.80412371], [6.55670103, 5.44329897], [2.73195876, 2.26804124], [7.64948454, 6.35051546], [8.74226804, 7.25773196], [7.64948454, 6.35051546], [1.09278351, 0.90721649], [0.54639175, 0.45360825]])) COMP3v4 3.0 4.0 inc2 1.0 3 0 2.0 4 1 3.0 27 1 4.0 7 3 5.0 14 8 6.0 5 14 7.0 6 14 8.0 0 2 9.0 0 1 COMP3v4 3.0 4.0 inc2 1.0 0.045455 0.000000 2.0 0.060606 0.022727 3.0 0.409091 0.022727 4.0 0.106061 0.068182 5.0 0.212121 0.181818 6.0 0.075758 0.318182 7.0 0.090909 0.318182 8.0 0.000000 0.045455 9.0 0.000000 0.022727 chi-square,p value,expected counts for 4 to 3 comparison (39.83581111870586, 3.4373880915658388e-06, 8, array([[ 1.8, 1.2], [ 3. , 2. ], [16.8, 11.2], [ 6. , 4. ], [13.2, 8.8], [11.4, 7.6], [12. , 8. ], [ 1.2, 0.8], [ 0.6, 0.4]]))

runfile('C:/Users/sockm/Documents/Data Academy/Data Management and Visualization Course/Mod 2 Data Analysis Tools/DAT Working Python/Week 2 Chi TEst/Chi Test Week2 Assignment Working.py', wdir='C:/Users/sockm/Documents/Data Academy/Data Management and Visualization Course/Mod 2 Data Analysis Tools/DAT Working Python/Week 2 Chi TEst') Urban Rate Deviation count 203.000000 mean 56.769360 std 23.844933 min 10.400000 25% 36.830000 50% 57.940000 75% 74.210000 max 100.000000 Name: urbanrate, dtype: float64 Income Per Person Deviation count 190.000000 mean 8740.966076 std 14262.809083 min 103.775857 25% 748.245151 50% 2553.496056 75% 9379.891165 max 105147.437697 Name: incomeperperson, dtype: float64 urban rate levels income rate levels inc2 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0 urb2 1.0 10 2 7 0 0 1 0 1 0 2.0 18 14 11 2 6 2 0 0 0 3.0 3 4 27 7 14 5 6 0 0 4.0 0 1 1 3 8 14 14 2 1 inc2 1.0 2.0 3.0 4.0 ... 6.0 7.0 8.0 9.0 urb2 ... 1.0 0.322581 0.095238 0.152174 0.000000 ... 0.045455 0.0 0.333333 0.0 2.0 0.580645 0.666667 0.239130 0.166667 ... 0.090909 0.0 0.000000 0.0 3.0 0.096774 0.190476 0.586957 0.583333 ... 0.227273 0.3 0.000000 0.0 4.0 0.000000 0.047619 0.021739 0.250000 ... 0.636364 0.7 0.666667 1.0

[4 rows x 9 columns] chi-square value, p value, expected counts FOR ALL (129.83783523184445, 1.6598113194807335e-16, 24, array([[ 3.53804348, 2.39673913, 5.25 , 1.36956522, 3.19565217, 2.51086957, 2.2826087 , 0.3423913 , 0.11413043], [ 8.92934783, 6.04891304, 13.25 , 3.45652174, 8.06521739, 6.33695652, 5.76086957, 0.86413043, 0.28804348], [11.11956522, 7.5326087 , 16.5 , 4.30434783, 10.04347826, 7.89130435, 7.17391304, 1.07608696, 0.35869565], [ 7.41304348, 5.02173913, 11. , 2.86956522, 6.69565217, 5.26086957, 4.7826087 , 0.7173913 , 0.23913043]])) COMP1v3 1.0 3.0 inc2 1.0 10 3 2.0 2 4 3.0 7 27 4.0 0 7 5.0 0 14 6.0 1 5 7.0 0 6 8.0 1 0 COMP1v3 1.0 3.0 inc2 1.0 0.476190 0.045455 2.0 0.095238 0.060606 3.0 0.333333 0.409091 4.0 0.000000 0.106061 5.0 0.000000 0.212121 6.0 0.047619 0.075758 7.0 0.000000 0.090909 8.0 0.047619 0.000000 chi-square value, p value, expected counts for 3 to 1 comparison (32.208399443693565, 3.715715191724342e-05, 7, array([[ 3.13793103, 9.86206897], [ 1.44827586, 4.55172414], [ 8.20689655, 25.79310345], [ 1.68965517, 5.31034483], [ 3.37931034, 10.62068966], [ 1.44827586, 4.55172414], [ 1.44827586, 4.55172414], [ 0.24137931, 0.75862069]])) COMP2v3 2.0 3.0 inc2 1.0 18 3 2.0 14 4 3.0 11 27 4.0 2 7 5.0 6 14 6.0 2 5 7.0 0 6 COMP2v3 2.0 3.0 inc2 1.0 0.339623 0.045455 2.0 0.264151 0.060606 3.0 0.207547 0.409091 4.0 0.037736 0.106061 5.0 0.113208 0.212121 6.0 0.037736 0.075758 7.0 0.000000 0.090909 chi-square,p value,expected counts for 3 to 2 comparison (35.27093727744174, 3.8186749006078295e-06, 6, array([[ 9.35294118, 11.64705882], [ 8.01680672, 9.98319328], [16.92436975, 21.07563025], [ 4.00840336, 4.99159664], [ 8.90756303, 11.09243697], [ 3.11764706, 3.88235294], [ 2.67226891, 3.32773109]])) COMP4v3 3.0 4.0 inc2 1.0 3 0 2.0 4 1 3.0 27 1 4.0 7 3 5.0 14 8 6.0 5 14 7.0 6 14 8.0 0 2 9.0 0 1 COMP4v3 3.0 4.0 inc2 1.0 0.045455 0.000000 2.0 0.060606 0.022727 3.0 0.409091 0.022727 4.0 0.106061 0.068182 5.0 0.212121 0.181818 6.0 0.075758 0.318182 7.0 0.090909 0.318182 8.0 0.000000 0.045455 9.0 0.000000 0.022727 chi-square,p value,expected counts for 3 to 4 comparison (39.83581111870586, 3.4373880915658388e-06, 8, array([[ 1.8, 1.2], [ 3. , 2. ], [16.8, 11.2], [ 6. , 4. ], [13.2, 8.8], [11.4, 7.6], [12. , 8. ], [ 1.2, 0.8], [ 0.6, 0.4]])) COMP1v4 1.0 4.0 inc2 1.0 10 0 2.0 2 1 3.0 7 1 4.0 0 3 5.0 0 8 6.0 1 14 7.0 0 14 8.0 1 2 9.0 0 1 COMP1v4 1.0 4.0 inc2 1.0 0.476190 0.000000 2.0 0.095238 0.022727 3.0 0.333333 0.022727 4.0 0.000000 0.068182 5.0 0.000000 0.181818 6.0 0.047619 0.318182 7.0 0.000000 0.318182 8.0 0.047619 0.045455 9.0 0.000000 0.022727 chi-square value, p value, expected counts for 4 to 1 comparison (50.63469516594517, 3.085426962262538e-08, 8, array([[ 3.23076923, 6.76923077], [ 0.96923077, 2.03076923], [ 2.58461538, 5.41538462], [ 0.96923077, 2.03076923], [ 2.58461538, 5.41538462], [ 4.84615385, 10.15384615], [ 4.52307692, 9.47692308], [ 0.96923077, 2.03076923], [ 0.32307692, 0.67692308]])) COMP2v4 2.0 4.0 inc2 1.0 18 0 2.0 14 1 3.0 11 1 4.0 2 3 5.0 6 8 6.0 2 14 7.0 0 14 8.0 0 2 9.0 0 1C:\Users\sockm\anaconda3\lib\site-packages\seaborn\categorical.py:3669: UserWarning: The `factorplot` function has been renamed to `catplot`. The original name will be removed in a future release. Please update your code. Note that the default `kind` in `factorplot` (`'point'`) has changed `'strip'` in `catplot`. warnings.warn(msg)

COMP2v4 2.0 4.0 inc2 1.0 0.339623 0.000000 2.0 0.264151 0.022727 3.0 0.207547 0.022727 4.0 0.037736 0.068182 5.0 0.113208 0.181818 6.0 0.037736 0.318182 7.0 0.000000 0.318182 8.0 0.000000 0.045455 9.0 0.000000 0.022727 chi-square,p value,expected counts for 4 to 2 comparison (63.79990198480764, 8.330827897764254e-11, 8, array([[9.83505155, 8.16494845], [8.19587629, 6.80412371], [6.55670103, 5.44329897], [2.73195876, 2.26804124], [7.64948454, 6.35051546], [8.74226804, 7.25773196], [7.64948454, 6.35051546], [1.09278351, 0.90721649], [0.54639175, 0.45360825]])) COMP3v4 3.0 4.0 inc2 1.0 3 0 2.0 4 1 3.0 27 1 4.0 7 3 5.0 14 8 6.0 5 14 7.0 6 14 8.0 0 2 9.0 0 1 COMP3v4 3.0 4.0 inc2 1.0 0.045455 0.000000 2.0 0.060606 0.022727 3.0 0.409091 0.022727 4.0 0.106061 0.068182 5.0 0.212121 0.181818 6.0 0.075758 0.318182 7.0 0.090909 0.318182 8.0 0.000000 0.045455 9.0 0.000000 0.022727 chi-square,p value,expected counts for 4 to 3 comparison (39.83581111870586, 3.4373880915658388e-06, 8, array([[ 1.8, 1.2], [ 3. , 2. ], [16.8, 11.2], [ 6. , 4. ], [13.2, 8.8], [11.4, 7.6], [12. , 8. ], [ 1.2, 0.8], [ 0.6, 0.4]]))

0 notes