quadratablog

[quadratablog]

I’ll be speaking at the MAA Epadel Conference (March 29, near Harrisburg, PA), and to celebrate, I made two logic puzzles. Solutions, more info, and PDF versions are on my blog: https://quadratablog.blogspot.com/.../epadel-march-29th...

Rules are on the puzzles but I'll summarize here.

Fill in the grid so that:

1. Each row, column, and 3×3 square cage contains the numbers 1 through 9 exactly once.

2. Circles mean the sum of adjacent cells is 9.

3. Diamonds mean the absolute difference between adjacent cells is 2 (order does not matter).

4. If no symbol connects two adjacent cells in a cage, their sum is not 9 and their difference is not 2.

Some starting numbers are given as hints, but these puzzles actually would have unique solutions even without them.

The one with more starting clues is considerably easier than the other. Give it a try if you want a gentler challenge. Let me know if you solve either one!

[quadratablog]

View this post on Instagram

A post shared by William Paterson University (@wpunj)

Much thanks to all the people from WPU's Marketing and Public Relations team that helped promote my latest book!

[quadratablog]

Happy New Year! I'm starting 2025 off with a sudoku puzzle based around clues involving the numbers 2, 5, and 25. I'm including a mini sample square to help everyone see how the ruleset works. For more information, a PDF version, and the solution, visit https://quadratablog.blogspot.com/2025/01/happy-new-year-2025-puzzle.html

[quadratablog]

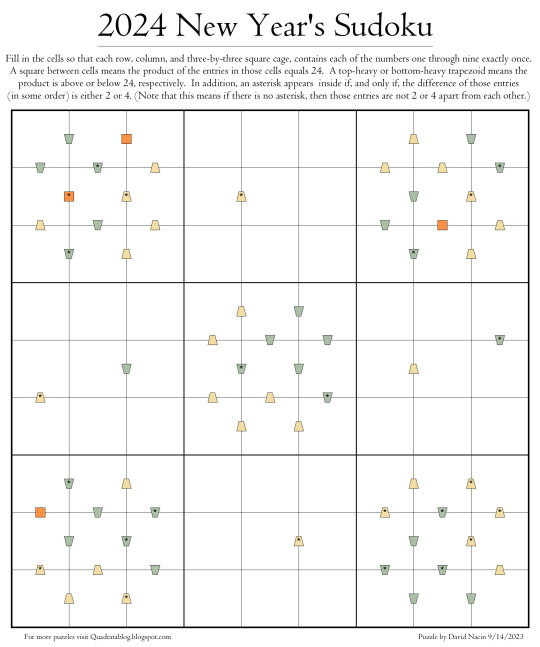
As 2024 is coming to a close, this is truly my last chance to share this puzzle. I created it a year ago but forgot to post it, so here it is now. My 2025 New Year's puzzle is coming soon! The solution and a PDF version of this puzzle can be found here: https://quadratablog.blogspot.com/2024/12/last-chance-2024-puzzle.html

[quadratablog]

Happy holidays everyone! Here's my latest snowflake puzzle, with instructions on the image. Solution, PDF version, and more info at: https://quadratablog.blogspot.com/2024/12/snowflake-puzzle-2024.html

[quadratablog]

I’m excited to share that my latest book is officially out now!

This unique book of mathematical puzzles also serves as an introduction to Group Theory. No prior background is needed, as all necessary mathematical concept are explained within the book. You can grab your copy today at the Springer website link below or find it on Amazon or other online retailers. I'd love for you to check it out, and feel free to let me know what you think!

https://www.jdoqocy.com/click-101294417-15150084?url=https%3A%2F%2Flink.springer.com%2Fbook%2F10.1007%2F978-3-031-70091-0

[quadratablog]

Here is a sudoku I made for the Fall MAA NJ-Section meeting last weekend, and now I want to share it here. The instructions explain everything needed but more details, a PDF, and the solution are on my blog at the following link:

[quadratablog]

The clues of this new puzzle involve the Fibonacci sequence 0,1,1,2,3,5,8,13,21,… (also known as the Pingala or Virahanka sequence.)

Fill in the cells with the numbers 1 through 7 so each number is used twice and adjacent cells get different numbers. Whenever the sum of the numbers in adjacent cells is a Fibonacci number, that sum is given as a clue. This means if there is no clue on an edge, the sum of those numbers is -not- a Fibonacci number.

The idea to use this particular graph to make a puzzle came from Tom Edgar, the editor of Math Horizons magazine. Three more of these will appear in the next issue of that publication soon. More information about the puzzle, the solution, and a high quality PDF version, can be found at the following link:

[quadratablog]

The clues here reveal whether the sum is less than, equal to, or greater than eleven. They also reveal whether the product is less than or greater than eleven. A solution, a PDF version, and some hints if you need help, can all be found on my blog here: https://quadratablog.blogspot.com/2024/10/eleven-sizedoku.html

[quadratablog]

In this new Sudoku puzzle, the clues reveal when one number is either 2,3,4 or 5 times another. Further instructions are on the puzzle. The solution, more info, and a PDF version can be found at http://quadratablog.blogspot.com/2023/09/small-multiples-sudoku.html

[quadratablog]

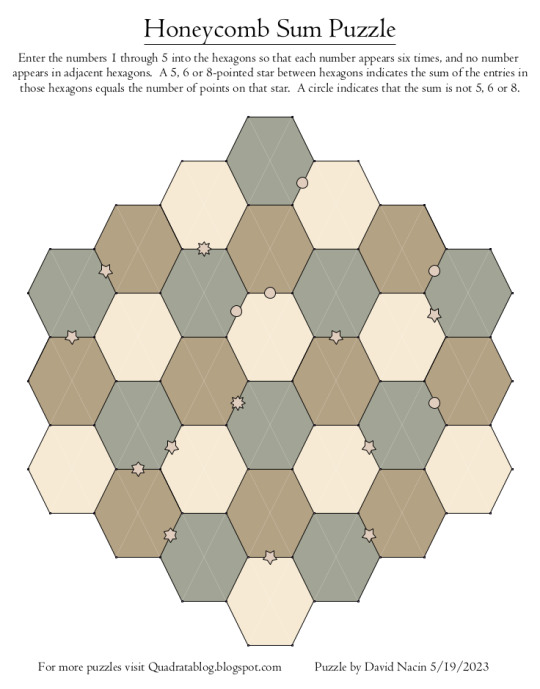
I feel spring is a good time for honeycomb puzzles.  Instructions are on the picture and both the solution and a PDF version are available at my website: http://quadratablog.blogspot.com

[quadratablog]

Here is one last 2023 Sudoku before we get too far into the year.  All the clues are based on the numbers 2, 3, and 23.  A solution and PDF version are at https://quadratablog.blogspot.com/2023/02/2023-reprise.html.

[quadratablog]

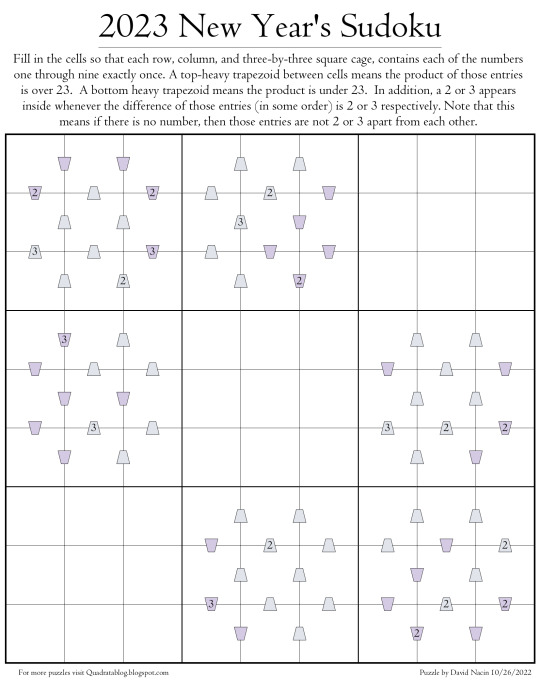
Here's a Sudoku I made for 2023 with clues using only the numbers 2,3, and 23.  The solution, a PDF version, and an easier version of the puzzle with more clues can all be found at: https://quadratablog.blogspot.com/2022/11/2023-new-years-puzzle.html

[quadratablog]

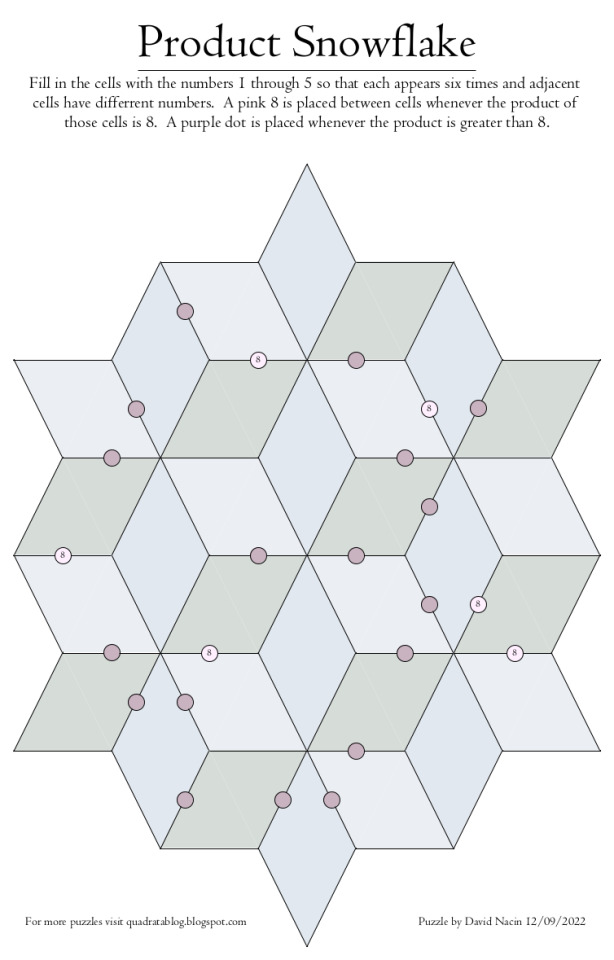
Here's a fairly easy puzzle that I whipped up this morning, with clues based on the size of the products of the numbers in adjacent cells. The solution and a higher quality PDF version can be found at https://quadratablog.blogspot.com/.

[quadratablog]

I recently posted a set-union puzzle so here's a new puzzle that uses set-intersections for clues.  Info on set-intersections, the solution, a PDF version, and more information can be found at: https://quadratablog.blogspot.com/2022/10/intersections.html #mtbos #math #maths #puzzles #puzzle

[quadratablog]

Here is a sudoku puzzle I made to commemorate my ten-year puzzle-creating anniversary.  More info, a PDF version, and the solution can be found at: https://quadratablog.blogspot.com/2022/08/10th-anniversary-of-puzzle-creation.html

[quadratablog]

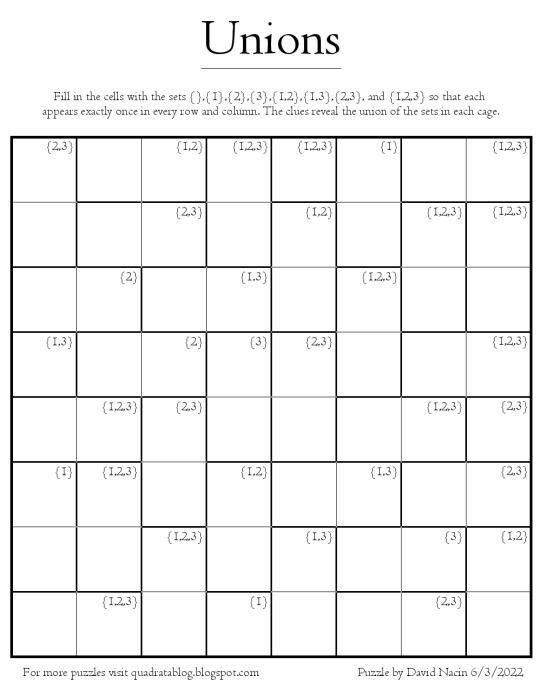
My new puzzle today is based on sets and their unions. The small amount of set theory needed to try it can be found on my blog, along with the solution and PDF at this link: https://quadratablog.blogspot.com/2022/07/unions.html