Text
Cardioids in Coffee Cups
Cardioids in Coffee Cups Numberphile have just done a nice video on how a cardioid shape is formed when a light is shone against the side of a mug. You can see this effect above (from the Numberphile video here). So, I decided to recreate this using Geogebra to get to understand some of the maths behind this shape. What is a cardioid? Cardioids can be formed by tracing a fixed point on a…

View On WordPress
0 notes
Text
Looking for a pre-Ice Age civilisation?
Looking for a pre-Ice Age civilisation? An interesting thought experiment is to consider the rise of modern civilisation and to ask whether civilisations could have risen in the long distant past. Let’s look at some graphs to see the plausibility of the climatic side of this. Firstly we can see on this graph (source here) that there was a rapid change in temperature following the end of the…
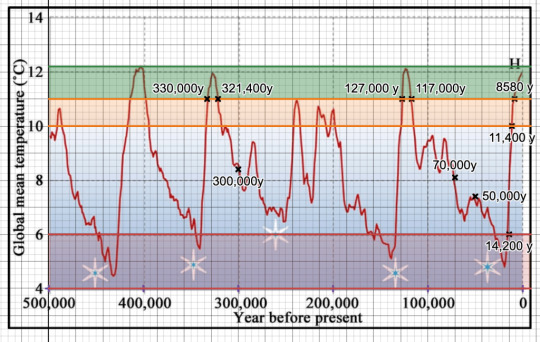
View On WordPress
0 notes
Text
FOBISIA Code Breaking Competition 2025
FOBISIA Code Breaking Competition 2025 Back by popular demand – we’re going to run the FOBISIA Code Breaking Maths Challenge again. Last year we had close to 120 schools taking part with over 22,000 students completing at least one code level. We hope that this year’s event will be equally successful. The dates will be: Between Monday 22nd and Friday 26th September 2025. If you are a teacher…

View On WordPress
0 notes
Text
Solar Gravitational lens: Seeing alien planets
Solar Gravitational lens: Seeing alien planets Let’s say in the future we pick up a signal from Proxima Centauri b – an exoplanet which is orbiting the star Proxima Centauri around 4.2 light years away. It would be nice to jump in a spaceship to explore further – but even travelling at 61,500km/h (the speed of Voyager 1) this would take a depressingly long 74,000 years. So, would the mysteries…
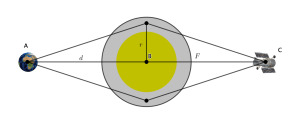
View On WordPress
0 notes
Text
Plotting asteroids - will 2024 YR4 hit Earth?
Plotting asteroids – will 2024 YR4 hit Earth? According to current estimates there is approximately a 1.6% chance of a collision between asteroid 2024 YR4 and Earth. This would not be an extinction level event – but could be enough to flatten a city. So I thought I’d work backwards from the calculated orbital paths calculated above by NASA above (citation) to arrive at an estimation for this…
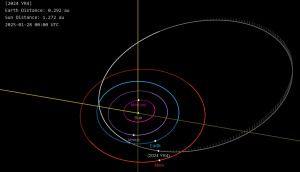
View On WordPress
0 notes
Text
Buffon's needle: Calculating pi
Buffon’s needle: Calculating pi The following problem, first posed in the 1700s by the Comte de Buffon has a surprising solution which can be used to generate pi. This is a nice example of probability games which can generate mathematical results over repeated trials (the Monte Carlo method). Here is the original problem: “Suppose we have a floor made of parallel strips of wood, each the same…

View On WordPress
0 notes
Text
Lattice based cryptography
Lattice based cryptography With the growing possibility of quantum computing being able to crack RSA encryption (the encryption technique which currently secures most banking and digital communications), the search is underway to find quantum-computing proof encryption. One potential possibility is lattice based cryptography – so I will explore the basics of this below! Creating a lattice To…
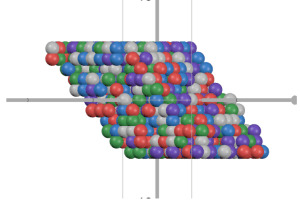
View On WordPress
0 notes
Text
A completely new Paper 2 for SL Applications students – this is my prediction for the May 2025 paper based on the style and trends for the questions currently being asked by IB examiners. This includes both a full question paper and full typed markscheme.
0 notes
Text
Predicted May 2025: SL Applications Paper 1
A completely new Paper 1 for SL Applications students – this is my prediction for the May 2025 paper based on the style and trends for the questions currently being asked by IB examiners. This includes both a full question paper and full typed markscheme.
0 notes
Text
Predicted May 2025: SL Analysis Paper 2
A completely new Paper 2 for SL Analysis students – this is my prediction for the May 2025 paper based on the style and trends for the questions currently being asked by IB examiners. This includes both a full question paper and full typed markscheme.
0 notes
Text
Predicted May 2025: SL Analysis Paper 1
A completely new Paper 1 for SL Analysis students – this is my prediction for the May 2025 paper based on the style and trends for the questions currently being asked by IB examiners. This includes both a full question paper and full typed markscheme.
0 notes
Text
Paper 3s for HL Applications
Six original Paper 3 investigations to support problem solving skills to prepare for the Paper 3 Higher Level paper. These investigations also are excellent for coursework explorations. Full markschemes also included.
0 notes
Text
Paper 3s for Analysis HL
Eight original Paper 3 investigations to support problem solving skills to prepare for the Paper 3 Higher Level paper. These investigations also are excellent for coursework explorations. Full markschemes also included.
0 notes
Text
Modelling Guide for IAs
A 60 page modelling guide to support students through all aspects of modelling tasks for the IB exploration.
0 notes
Text
Exploration Guide for IB Maths Coursework
A 65 pdf guide to support students and teachers through the process of the IB coursework
0 notes
Text
Maths and Evolutionary Biology
Maths and Evolutionary Biology Mathematics is often utilised across many fields – lets look at an example from biology, evolutionary biology and paleontology, in trying to understand the development of homo-sapiens. We can start with a large data set which gives us the data for mammal body mass and brain size in grams (downloaded from here). I then tidied up this to remove the rows with NA…

View On WordPress
0 notes