hoofclid-facts

[hoofclid-facts]

The technical term for these monsters is "Large Low Shear Velocity Provinces" (LLSVPs) or superplumes. They're named after geologists.

[hoofclid-facts]

Okay this may stretch the definition of "facts" but the first bit is true!!

And no one tell Pinkie that trilobites weren't around in the Cryogenian Period.

[hoofclid-facts]

[hoofclid-facts]

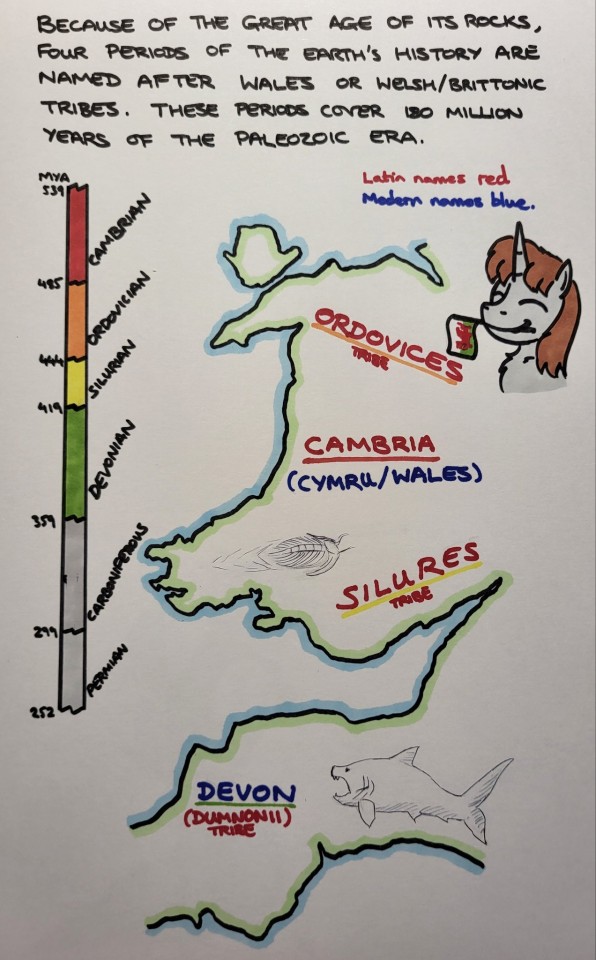
It may be stretching a point to call Devon "Welsh", but it was Welsh longer than most of the rest of England, and is named after a pre-Roman Brittonic tribe. A distinction it shares with Cornwall and, more curiously, Kent.

The fish is a Dunkleosteus, one of the largest Devonian fish. And I couldn't resist adding a trilobite.

[hoofclid-facts]

I don't think Hoofy realises our horses aren't as smart as he is.

[hoofclid-facts]

The site is now known as the Macellum of Pozzuoli, previously misindentified as "the Temple of Jupiter Serapis". It played a significant role in the early study of geology.

[Plain Text:

In the coastal town of Pozzuoli, in the vicinity of Vesuvius, are some curious columns which once formed part of a Roman marketplace.

They're curious because, four metres above ground, they are riddled with holes made by burrowing molluscs -- which live in the sea!

The volcanically active region has risen and fallen over the last 2000 years by (at least) seven metres due to the pressure of the magma beneath the surface. So the Roman columns had enough time in the sea to be damaged by the molluscs, before being lifted back out again!]

[hoofclid-facts]

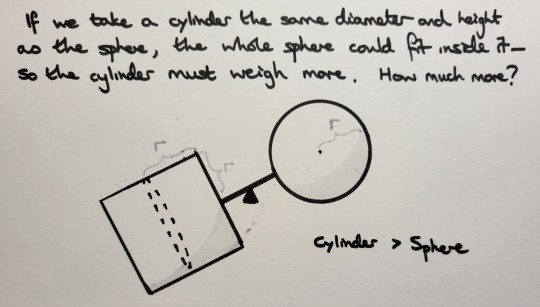
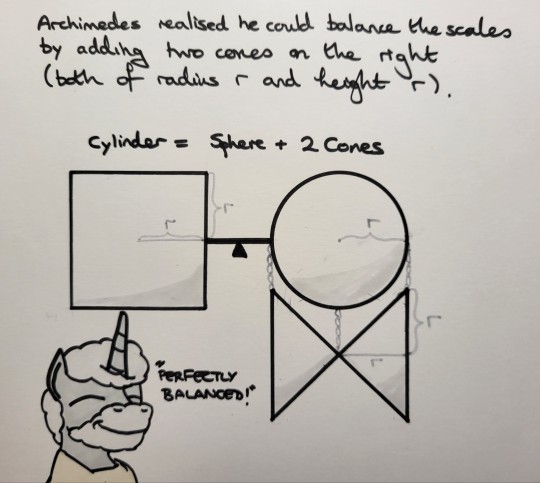
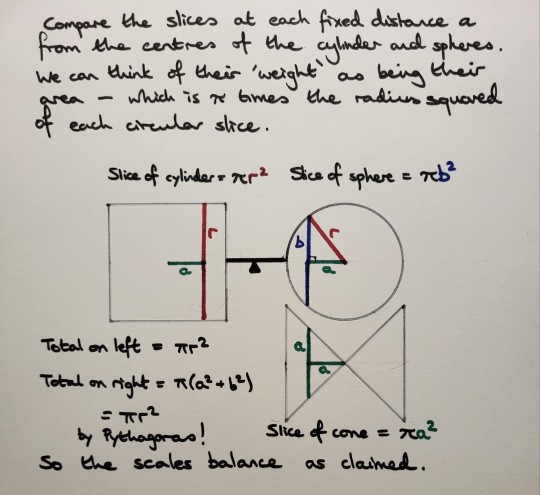
"Too many pis", Part 4 (of 4)

{Plain text:

The rediscovered text reveals that Archimedes discovered his theorems about volumes, area etc by effectively weighing the shapes using a lever. Let's try to weigh a sphere.

If we take a cylinder the same height and diameter as the sphere, the whole sphere could fit inside it, so the cylinder must weigh more. How much more? Archimedes realised he could balance the scales by adding two cones to the scales, both of height and radius r.

The best way to see why they balance is to slice all the shapes up into very thin slices. The cylinder, sphere and cones all have circular cross sections, so all the slices are circles.

Compare the slices at each fixed distance from the centres of the sphere and cylinder. We can think of their weight as being their area. By Pythagoras the slices of the cone and sphere exactly balance the slice of the cylinder. So the scales balance!

And since we already know the weight of the cylinder and cone, this tells us the weight of the sphere! }

[hoofclid-facts]

"Too many pis", Part 3

{Plain text:

Part 3

Why would Archimedes have a second, secret method to prove these results? Greek mathematical methods required a very high standard of rigour and, to do these methods successfully, you usually need a good idea what answer you're aiming for. So having another method that tells you the answer to seek is useful.

Archimedes: But these methods only allow theorems to be investigated, not proved.

Twilight: Shush. Give me the book.

However he did describe his methods in a letter to Eratosthenes, chief librarian at the Library of Alexandria. Copies were made down the centuries. The only one which survives today was made in the 10th century CE in Constantinople.

Although the book survives, it was lost for centuries. In the 13th century a monk, probably somewhere near Jerusalem, decided the valuable paper would be more useful as a prayer book and cleaned the ink off the paper to reuse it.

Twily: He WHAT?!

Fortunately he couldn't clean it completely. The text underneath survives as a "palimpsest": a sort of ghost text written at right angles to the prayer book.

The book turned up in the catalogue of a monastery library back in Constantinople in the 19th century, where a Danish scholar, Johan Heiberg, transcribed the hidden text and discovered the lost book in its pages!

The book vanished again -- stolen or traded illicitly -- for most of the 20th century, but is now owned by an unknown buyer who funded a full conservation and study programme.

Twilight: No stealing! This is my book, and I'm gonna read it!

To learn what Archimedes' Method was, come back for part 4. }

[hoofclid-facts]

"Too many pis" Part 2

Notes:

1) Actually computing the area of the 96-sided shape, Archimedes got the "22/7" estimate for pi that puts pi day on 22nd July (outside the USA)

2) I'm underselling Archimedes here a bit. I say "area area of the polygon approaches that of the circle" as if it's obvious, but really that needs proof too. This is the point of drawing a hexagon (and subsequent polygons) around the outside too -- you squeeze the circle from both sides to make sure the error tends to 0.

{Plain text:

The mathematician who discovered all these formulae for areas of circles, spheres and so on, and established the fundamental role of pi in mathematics, was the famous Archimedes. Let's take a look at how he did it.

What's the simplest thing that looks vaguely circular? A hexagon! What is the area of a hexagon? If you chop a hexagon into six triangles, and use "half base times height" on each triangle, we get a formula "half perimeter times height" which actually works for any regular polygon.

Let's squeeze our circle between two hexagons, one inside and one outside. Clearly the circle's area is somewhere between the two. The inside hexagon has perimeter 6r; if we guess its height is also about r, we get a first guess

Area of circle ~ 3r^2.

But clearly we've missed a big chunk of area between the circle and the hexagon. Archimedes solution to this is to add more sides to the polygon. Here's a 12 sided shape in a circle; as you see the "missing area" is much smaller this time (less than half what it was). So the 12-sided shape gives a better approximation than the hexagon!

[Hoofy: so hexagons aren't always the bestagons...?]

Imagine doing this over and over: a 24 sided shape, then a 48, and so on.... [Hoofy: I'm not drawing that, here's a Scoot instead.] The area gets closer and closer to the circle.

Our "half height times perimeter" formula still works for all these polygons. How does it change? The "height" gets closer and closer to r; and the perimeter gets closer and closer to the circumference of the circle -- which is 2 pi r. So the area of the polygon gets closer and closer to 1/2 x r = 2pi r; so the area of the circle must be pi r^2!

Archimedes: And I did the cylinders, spheres and so on in this same way, and don't have any other methods hidden in a secret book, honest!

Twi: secret book? }

[hoofclid-facts]

"Too many pis", Part 1

{Plain text:

We all learn formulae like "Area of circle = pi r^2" at school. But how much do we actually think about why these things are true, or who discovered them? [Hoofy inspecting formula with magnifying glass] And what business does pi have popping up everywhere? Look at all these formulae. [Circles, spheres etc]. Why is it the same number in all of them?! [One of the pi symbols hides a Pinkie. Soarin is drooling over all the pi]

In fact, it's not at all clear that these numbers are at all related. There was a good hundred year period where we simply didn't know that there was any relationship. One of the very earliest of the great Greek mathematicians, Eudoxus of Cnidus, proved that there are some numbers that make these formulae work. But he had no clue what exactly they were. These proofs come down to us through Book V of Euclid's Elements [Hoofy: Euclid? That name seems familiar...] But even Euclid gives no relations between the numbers.

Imagine if we never found out, and we had to remember a different symbol for every single equation!?

To meet the hero who rescued us from this fate, come back for Part 2! [Brae: you're doing a cliffhanger... in a maths talk?!]

}

[hoofclid-facts]

[Plain text:

Silkworm production first arrived in the Mediterranean world aa a result of smuggling by monks. To break the Chinese and Persian monopolies of silk production and trading, the Byzantine Emperor asked the monks to bring back silkworms -- which they did by hiding silkworm eggs inside hollow bamboo staffs.]

[hoofclid-facts]

With apologies for any inaccuracies in the script.

I really like the story of Hangeul; the King keeping his labour secret to make sure the entrenched scholar class couldn't thwart his script before it was ready. And it's incredibly logical! Well designed for the specific language that needed it, rather than the clunky hand-me-down script I'm using.

There is, so far as I know, no evidence of apple hatred in 15th century Korea.