datalearning

[datalearning]

Testing a Potential Moderator

Week4: Testing a Potential Moderator

 import pandas

import numpy

import seaborn

import scipy

import matplotlib.pyplot as plt

 

NESARC Dataset

nesarc = pandas.read_csv ('nesarc_pds.csv', low_memory=False)

 

# Show all columns in DataFrame

pandas.set_option('display.max_columns' , None)

 

# Show all rows in DataFrame

pandas.set_option('display.max_rows' , None)

nesarc.columns = map(str.upper , nesarc.columns)

pandas.set_option('display.float_format' , lambda x:'%f'%x)

 

# Convert variables to numeric

nesarc['AGE'] = nesarc['AGE'].convert_objects(convert_numeric=True)

nesarc['MAJORDEP12'] = nesarc['MAJORDEP12'].convert_objects(convert_numeric=True)

nesarc['S1Q231'] = nesarc['S1Q231'].convert_objects(convert_numeric=True)

nesarc['S3BQ1A5'] = nesarc['S3BQ1A5'].convert_objects(convert_numeric=True)

nesarc['S3BD5Q2E'] = nesarc['S3BD5Q2E'].convert_objects(convert_numeric=True)

 

# Subset

subset1 = nesarc[(nesarc['AGE']>=18) & (nesarc['AGE']<=30) & nesarc['S3BQ1A5']==1]     # Ages 18-30, cannabis users

subsetc1 = subset1.copy()

 

# Setting missing data

subsetc1['S1Q231']=subsetc1['S1Q231'].replace(9, numpy.nan)

subsetc1['S3BQ1A5']=subsetc1['S3BQ1A5'].replace(9, numpy.nan)

subsetc1['S3BD5Q2E']=subsetc1['S3BD5Q2E'].replace(99, numpy.nan)

subsetc1['S3BD5Q2E']=subsetc1['S3BD5Q2E'].replace('BL', numpy.nan)

 

recode1 = {1: 9, 2: 8, 3: 7, 4: 6, 5: 5, 6: 4, 7: 3, 8: 2, 9: 1}     # Frequency of cannabis use variable reverse-recode

subsetc1['CUFREQ'] = subsetc1['S3BD5Q2E'].map(recode1)     # Change the variable name from S3BD5Q2E to CUFREQ

subsetc1['CUFREQ'] = subsetc1['CUFREQ'].astype('category')

 

# Raname graph labels for better interpetation

subsetc1['CUFREQ'] = subsetc1['CUFREQ'].cat.rename_categories(["2 times/year","3-6 times/year","7-11 times/year","Once a month","2-3 times/month","1-2 times/week","3-4 times/week","Nearly every day","Every day"])

 

## Contingency table of observed counts of major depression diagnosis (response variable) within frequency of cannabis use groups (explanatory variable), in ages 18-30

contab1 = pandas.crosstab(subsetc1['MAJORDEP12'], subsetc1['CUFREQ'])

print (contab1)

 

# Column percentages

colsum=contab1.sum(axis=0)

colpcontab=contab1/colsum

print(colpcontab)

 

# Chi-square calculations for major depression within frequency of cannabis use groups

print ('Chi-square value, p value, expected counts, for major depression within cannabis use status')

chsq1= scipy.stats.chi2_contingency(contab1)

print (chsq1)

 

# Bivariate bar graph for major depression percentages with each cannabis smoking frequency group

plt.figure(figsize=(12,4))     # Change plot size

ax1 = seaborn.factorplot(x="CUFREQ", y="MAJORDEP12", data=subsetc1, kind="bar", ci=None)

ax1.set_xticklabels(rotation=40, ha="right")    # X-axis labels rotation

plt.xlabel('Frequency of cannabis use')

plt.ylabel('Proportion of Major Depression')

plt.show()

 

recode2 = {1: 10, 2: 9, 3: 8, 4: 7, 5: 6, 6: 5, 7: 4, 8: 3, 9: 2, 10: 1}   # Frequency of cannabis use variable reverse-recode

subsetc1['CUFREQ2'] = subsetc1['S3BD5Q2E'].map(recode2)      # Change the variable name from S3BD5Q2E to CUFREQ2

 

sub1=subsetc1[(subsetc1['S1Q231']== 1)]

sub2=subsetc1[(subsetc1['S1Q231']== 2)]

 

print ('Association between cannabis use status and major depression for those who lost a family member or a close friend in the last 12 months')

contab2=pandas.crosstab(sub1['MAJORDEP12'], sub1['CUFREQ2'])

print (contab2)

 

# Column percentages

colsum2=contab2.sum(axis=0)

colpcontab2=contab2/colsum2

print(colpcontab2)

 

# Chi-square

print ('Chi-square value, p value, expected counts')

chsq2= scipy.stats.chi2_contingency(contab2)

print (chsq2)

 

# Line graph for major depression percentages within each frequency group, for those who lost a family member or a close friend

plt.figure(figsize=(12,4))     # Change plot size

ax2 = seaborn.factorplot(x="CUFREQ", y="MAJORDEP12", data=sub1, kind="point", ci=None)

ax2.set_xticklabels(rotation=40, ha="right")     # X-axis labels rotation

plt.xlabel('Frequency of cannabis use')

plt.ylabel('Proportion of Major Depression')

plt.title('Association between cannabis use status and major depression for those who lost a family member or a close friend in the last 12 months')

plt.show()

print ('Association between cannabis use status and major depression for those who did NOT lose a family member or a close friend in the last 12 months')

contab3=pandas.crosstab(sub2['MAJORDEP12'], sub2['CUFREQ2'])

print (contab3)

 

# Column percentages

colsum3=contab3.sum(axis=0)

colpcontab3=contab3/colsum3

print(colpcontab3)

 

# Chi-square

print ('Chi-square value, p value, expected counts')

chsq3= scipy.stats.chi2_contingency(contab3)

print (chsq3)

 

# Line graph for major depression percentages within each frequency group, for those who did NOT lose a family member or a close friend

plt.figure(figsize=(12,4))     # Change plot size

ax3 = seaborn.factorplot(x="CUFREQ", y="MAJORDEP12", data=sub2, kind="point", ci=None)

ax3.set_xticklabels(rotation=40, ha="right")     # X-axis labels rotation

plt.xlabel('Frequency of cannabis use')

plt.ylabel('Proportion of Major Depression')

plt.title('Association between cannabis use status and major depression for those who did NOT lose a family member or a close friend in the last 12 months')

plt.show()

Analysis on Testing a Potential Moderator:

Interpretation of statistical interaction between frequency of cannabis use (10-level categorical explanatory, variable ”S3BD5Q2E”) and major depression diagnosis in the last 12 months (categorical response, variable ”MAJORDEP12”), moderated by variable “S1Q231“ (categorical), which indicates the total number of the people who lost a family member or a close friend in the last 12 months.

 

A Chi Square test of independence revealed that among cannabis users aged between 18 and 30 years old (subsetc1), the frequency of cannabis use (explanatory variable collapsed into 9 ordered categories) and past year depression diagnosis (response binary categorical variable) were significantly associated, X2 =29.83, 8 df, p=0.00022.

The bivariate graph (C->C) below, shows correlation between frequency of cannabis use (explanatory variable) and major depression diagnosis in the past year (response variable). Left-skewed distribution, indicates that the more an individual (18-30) smoked cannabis, the better were the chances to have experienced depression in the last 12 months.

For the moderating variable equal to 1, which is those whose family member or a close friend died in the last 12 months (sub1), a Chi Square test of independence revealed that among cannabis users aged between 18 and 30 years old, the frequency of cannabis use (explanatory variable) and past year depression diagnosis (response variable) were not significantly associated, X2 =4.61, 9 df, p=0.86. As a result, since the chi-square value is quite small and the p-value is significantly large, we can assume that there is no statistical relationship between these two variables, when taking into account the subgroup of individuals who lost a family member or a close friend in the last 12 months.

The bivariate line graph (C->C) below, shows the correlation between frequency of cannabis use (explanatory variable) and major depression diagnosis in the past year (response variable), in the subgroup of individuals whose a family member or a close friend died in the last 12 months (sub1). In fact, the direction of the distribution (fluctuation) does not indicate a positive relationship between these two variables, for those who experienced a family/close death in the past year.

Subsequently, for the moderating variable equal to 2, which is those whose a family member or a close friend did not die in the last 12 months (sub2), a Chi Square test of independence revealed that among cannabis users aged between 18 and 30 years old, the frequency of cannabis use (explanatory variable) and past year depression diagnosis (response variable) were significantly associated, X2 =37.02, 9 df, p=2.6e-05 (p-value is written in scientific notation). As a result, since the chi-square value is quite large and the p-value is significantly small, we can assume that there is a positive relationship between these two variables, when taking into account the subgroup of individuals who did not lose a family member or a close friend in the last 12 months.

The bivariate line graph (C->C) below, shows the correlation between frequency of cannabis use (explanatory variable) and major depression diagnosis in the past year (response variable), in the subgroup of individuals whose a family member or a close friend did not die in the last 12 months (sub2). Obviously, the direction of the distribution indicates a positive relationship between these two variables, which means that the frequency of cannabis use directly affects the proportions of major depression, regarding the individuals who did not experience a family/close death in the last 12 months.

Summary of Interpretation

It seems that both the direction and the size of the relationship between frequency of cannabis use and major depression diagnosis in the last 12 months, is heavily affected by a death of a family member or a close friend in the same period. In other words, when the incident of a family/close death is present, the correlation is considerably weak, whereas when it is absent, the correlation is significantly strong and positive. Thus, the third variable moderates the association between cannabis use frequency and major depression diagnosis.

[datalearning]

Correlation Coefficient

Week3: Generating a Correlation Coefficient:

import pandas

import numpy

import seaborn

import scipy

import matplotlib.pyplot as plt

 

NESARC Dataset

 

nesarc = pandas.read_csv ('nesarc_pds.csv' , low_memory=False)

 

# Show all columns in DataFrame

pandas.set_option('display.max_columns', None)

 

# Show all rows in DataFrame

pandas.set_option('display.max_rows', None)

 

nesarc.columns = map(str.upper , nesarc.columns)

 

pandas.set_option('display.float_format' , lambda x:'%f'%x)

 

# Convert variables to numeric

 

nesarc['AGE'] = pandas.to_numeric(nesarc['AGE'], errors='coerce')

nesarc['S3BQ4'] = pandas.to_numeric(nesarc['S3BQ4'], errors='coerce')

nesarc['S4AQ6A'] = pandas.to_numeric(nesarc['S4AQ6A'], errors='coerce')

nesarc['S3BD5Q2F'] = pandas.to_numeric(nesarc['S3BD5Q2F'], errors='coerce')

nesarc['S9Q6A'] = pandas.to_numeric(nesarc['S9Q6A'], errors='coerce')

nesarc['S4AQ7'] = pandas.to_numeric(nesarc['S4AQ7'], errors='coerce')

nesarc['S3BQ1A5'] = pandas.to_numeric(nesarc['S3BQ1A5'], errors='coerce')

 

# Subset

 

subset1 = nesarc[(nesarc['S3BQ1A5']==1)]    # Cannabis users

subsetc1 = subset1.copy()

 

# Setting missing data

 

subsetc1['S3BQ1A5']=subsetc1['S3BQ1A5'].replace(9, numpy.nan)

subsetc1['S3BD5Q2F']=subsetc1['S3BD5Q2F'].replace('BL', numpy.nan)

subsetc1['S3BD5Q2F']=subsetc1['S3BD5Q2F'].replace(99, numpy.nan)

subsetc1['S4AQ6A']=subsetc1['S4AQ6A'].replace('BL', numpy.nan)

subsetc1['S4AQ6A']=subsetc1['S4AQ6A'].replace(99, numpy.nan)

subsetc1['S9Q6A']=subsetc1['S9Q6A'].replace('BL', numpy.nan)

subsetc1['S9Q6A']=subsetc1['S9Q6A'].replace(99, numpy.nan)

 

# Scatterplot for the age when began using cannabis the most and the age of first episode of major depression

 

plt.figure(figsize=(12,4))      # Change plot size

scat1 = seaborn.regplot(x="S3BD5Q2F", y="S4AQ6A", fit_reg=True, data=subset1)

plt.xlabel('Age when began using cannabis the most')

plt.ylabel('Age when expirenced the first episode of major depression')

plt.title('Scatterplot for the age when began using cannabis the most and the age of first the episode of major depression')

plt.show()

 

data_clean=subset1.dropna()

 

# Pearson correlation coefficient for the age when began using cannabis the most and the age of first the episode of major depression

 

print ('Association between the age when began using cannabis the most and the age of the first episode of major depression')

print (scipy.stats.pearsonr(data_clean['S3BD5Q2F'], data_clean['S4AQ6A']))

 

# Scatterplot for the age when began using cannabis the most and the age of the first episode of general anxiety

 

plt.figure(figsize=(12,4))      # Change plot size

scat2 = seaborn.regplot(x="S3BD5Q2F", y="S9Q6A", fit_reg=True, data=subset1)

plt.xlabel('Age when began using cannabis the most')

plt.ylabel('Age when expirenced the first episode of general anxiety')

plt.title('Scatterplot for the age when began using cannabis the most and the age of the first episode of general anxiety')

plt.show()

 

# Pearson correlation coefficient for the age when began using cannabis the most and the age of the first episode of general anxiety

 

print ('Association between the age when began using cannabis the most and the age of first the episode of general anxiety')

print (scipy.stats.pearsonr(data_clean['S3BD5Q2F'], data_clean['S9Q6A']))

Generating a Correlation Coefficient:

This assignment aims the correlation between the age when the individuals began using cannabis the most (quantitative explanatory, variable “S3BD5Q2F”) and the age when they experienced the first episode of major depression and general anxiety (quantitative response, variables “S4AQ6A” and ”S9Q6A”).

The scatterplot illustrates the correlation between the age when individuals began using cannabis the most (quantitative explanatory variable) and the age when they experienced the first episode of depression (quantitative response variable). The direction of the relationship is positive (increasing), which means that an increase in the age of cannabis use is associated with an increase in the age of the first depression episode. In addition, since the points are scattered about a line, the relationship is linear. Regarding the strength of the relationship, from the pearson correlation test, the correlation coefficient is equal to 0.23, which indicates a weak linear relationship between the two quantitative variables. The associated p-value is equal to 2.27e-09 (p-value is written in scientific notation) and the fact that it is very small which indicates that the relationship is statistically significant. As a result, the association between the age when began using cannabis the most and the age of the first depression episode is moderately weak, but it is highly unlikely that a relationship of this magnitude would be due to chance alone. Finally, by squaring the r, the fraction of the variability of one variable that can be predicted by the other, which is low at 0.05.

 

For the association between the age when individuals began using cannabis the most (quantitative explanatory variable) and the age when they experienced the first episode of anxiety (quantitative response variable), the scatterplot shows a positive linear relationship. Regarding the strength of the relationship, the pearson correlation test indicates that the correlation coefficient is equal to 0.14, which is interpreted to a weak linear relationship between the two quantitative variables. The associated p-value is equal to 0.0001, which indicates that the relationship is statistically significant. Therefore, the association between the age when began using cannabis the most and the age of the first anxiety episode is weak, but it is highly unlikely that a relationship of this magnitude would be due to chance alone. Finally, by squaring the r, the fraction of the variability of one variable that can be predicted by the other, which is very low at 0.01.

[datalearning]

Chi-Square Test

Week2: Running a Chi-Square Test of Independence

import pandas

import numpy

import scipy.stats

import seaborn

import matplotlib.pyplot as plt

NESARC Dataset

nesarc = pandas.read_csv ('nesarc_pds.csv' , low_memory=False)

#Show all columns in DataFrame

pandas.set_option('display.max_columns', None)

#Show all rows in DataFrame

pandas.set_option('display.max_rows', None)

nesarc.columns = map(str.upper , nesarc.columns)

pandas.set_option('display.float_format' , lambda x:'%f'%x)

 

# Convert variables to numeric

nesarc['AGE'] = pandas.to_numeric(nesarc['AGE'], errors='coerce')

nesarc['S3BQ4'] = pandas.to_numeric(nesarc['S3BQ4'], errors='coerce')

nesarc['S3BQ1A5'] = pandas.to_numeric(nesarc['S3BQ1A5'], errors='coerce')

nesarc['S3BD5Q2B'] = pandas.to_numeric(nesarc['S3BD5Q2B'], errors='coerce')

nesarc['S3BD5Q2E'] = pandas.to_numeric(nesarc['S3BD5Q2E'], errors='coerce')

nesarc['MAJORDEP12'] = pandas.to_numeric(nesarc['MAJORDEP12'], errors='coerce')

nesarc['GENAXDX12'] = pandas.to_numeric(nesarc['GENAXDX12'], errors='coerce')

 

# Data for Ages 18-30

subset1 = nesarc[(nesarc['AGE']>=18) & (nesarc['AGE']<=30)]     

subsetc1 = subset1.copy()

 

# Cannabis users, ages 18-30

subset2 = nesarc[(nesarc['AGE']>=18) & (nesarc['AGE']<=30) & (nesarc['S3BQ1A5']==1)]   

subsetc2 = subset2.copy()

 

# Setting missing data for frequency and cannabis use, variables S3BD5Q2E, S3BQ1A5

 

subsetc1['S3BQ1A5']=subsetc1['S3BQ1A5'].replace(9, numpy.nan)

subsetc2['S3BD5Q2E']=subsetc2['S3BD5Q2E'].replace('BL', numpy.nan)

subsetc2['S3BD5Q2E']=subsetc2['S3BD5Q2E'].replace(99, numpy.nan)

 

# Contingency table of observed counts of major depression diagnosis

(response variable) within cannabis use (explanatory variable), in ages 18-30

 

contab1=pandas.crosstab(subsetc1['MAJORDEP12'], subsetc1['S3BQ1A5'])

print (contab1)

 

# Column percentages

colsum=contab1.sum(axis=0)

colpcontab=contab1/colsum

print(colpcontab)

 

# Chi-square calculations for major depression within cannabis use status

print ('Chi-square value, p value, expected counts, for major depression within cannabis use status')

chsq1= scipy.stats.chi2_contingency(contab1)

print (chsq1)

 

# Contingency table of observed counts of general anxiety diagnosis(response variable) within cannabis use (explanatory variable), in ages 18-30

contab2=pandas.crosstab(subsetc1['GENAXDX12'], subsetc1['S3BQ1A5'])

print (contab2)

 

# Column percentages

colsum2=contab2.sum(axis=0)

colpcontab2=contab2/colsum2

print(colpcontab2)

 

# Chi-square calculations for general anxiety within cannabis use status

print ('Chi-square value, p value, expected counts, for general anxiety within cannabis use status')

chsq2= scipy.stats.chi2_contingency(contab2)

print (chsq2)

 

# Contingency table for observed counts of major depression diagnosis(response variable) and frequency of cannabis use (10 level explanatory variable), between age 18-30

contab3=pandas.crosstab(subset2['MAJORDEP12'], subset2['S3BD5Q2E'])

print (contab3)

 

# Column percentages

colsum3=contab3.sum(axis=0)

colpcontab3=contab3/colsum3

print(colpcontab3)

 

# Chi-square calculations for major depression within frequency of cannabis use groups

print ('Chi-square value, p value, expected counts for major depression associated frequency of cannabis use')

chsq3= scipy.stats.chi2_contingency(contab3)

print (chsq3)

 

# Dictionary with details of frequency variable reverse-recode

recode1 = {1: 9, 2: 8, 3: 7, 4: 6, 5: 5, 6: 4, 7: 3, 8: 2, 9: 1} 

 

# Change variable name from S3BD5Q2E to CUFREQ

subsetc2['CUFREQ'] = subsetc2['S3BD5Q2E'].map(recode1)    

subsetc2["CUFREQ"] = subsetc2["CUFREQ"].astype('category')

 

# Rename graph labels for better interpretation

subsetc2['CUFREQ'] = subsetc2['CUFREQ'].cat.rename_categories(["2 times/year","3-6 times/year","7-11 times/years","Once a month","2-3 times/month","1-2 times/week","3-4 times/week","Nearly every day","Every day"])

 

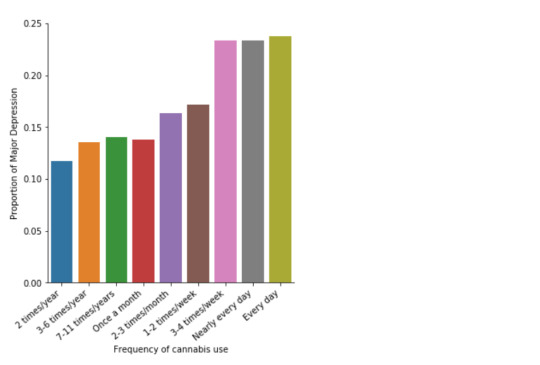
# Graph percentages of major depression within each cannabis smoking frequency group

plt.figure(figsize=(12,4))      # Change plot size

ax1 = seaborn.factorplot(x="CUFREQ", y="MAJORDEP12", data=subsetc2, kind="bar", ci=None)

ax1.set_xticklabels(rotation=40, ha="right")    # X-axis labels rotation

plt.xlabel('Frequency of cannabis use')

plt.ylabel('Proportion of Major Depression')

plt.show()

 

# Post hoc test, pair comparison of frequency groups 1 and 9, 'Every day' and '2 times a year'

recode2 = {1: 1, 9: 9}

subsetc2['COMP1v9']= subsetc2['S3BD5Q2E'].map(recode2)

 

# Contingency table of observed counts

ct4=pandas.crosstab(subsetc2['MAJORDEP12'], subsetc2['COMP1v9'])

print (ct4)

 

# Column percentages

colsum4=ct4.sum(axis=0)

colpcontab4=ct4/colsum4

print(colpcontab4)

 

# Chi-square calculations for pair comparison of frequency groups 1 and 9, 'Every day' and '2 times a year'

print ('Chi-square value, p value, expected counts, for pair comparison of frequency groups -Every day- and -2 times a year-')

cs4= scipy.stats.chi2_contingency(ct4)

print (cs4)

 

# Post hoc test, pair comparison of frequency groups 2 and 6, 'Nearly every day' and 'Once a month'

recode3 = {2: 2, 6: 6}

subsetc2['COMP2v6']= subsetc2['S3BD5Q2E'].map(recode3)

 

# Contingency table of observed counts

ct5=pandas.crosstab(subsetc2['MAJORDEP12'], subsetc2['COMP2v6'])

print (ct5)

 

# Column percentages

colsum5=ct5.sum(axis=0)

colpcontab5=ct5/colsum5

print(colpcontab5)

# Chi-square calculations for pair comparison of frequency groups 2 and 6, 'Nearly every day' and 'Once a month'

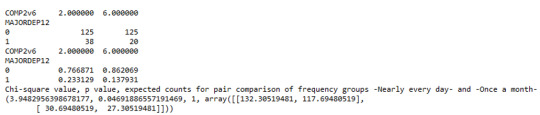
print ('Chi-square value, p value, expected counts for pair comparison of frequency groups -Nearly every day- and -Once a month-')

cs5= scipy.stats.chi2_contingency(ct5)

print (cs5)

Model Interpretation for Chi-Square Tests:

When examining the patterns of association between major depression (categorical response variable) and cannabis use status (categorical explanatory variable), a chi-square test of independence revealed that among young adults aged between 18 and 30 years old (subsetc1), those who were cannabis users, were more likely to have been diagnosed with major depression in the last 12 months (18%), compared to the non-users (8.4%), X2 =171.6, 1 df, p=3.16e-39 (p-value is written in scientific notation). As a result, since our p-value is extremely small, the data provides significant evidence against the null hypothesis. Thus, we reject the null hypothesis and accept the alternate hypothesis, which indicates that there is a positive correlation between cannabis use and depression diagnosis.

Output

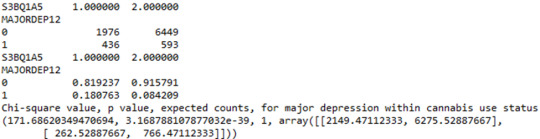
When examining the patterns of association between major depression (categorical response variable) and cannabis use status (categorical explanatory variable), a chi-square test of independence revealed that among young adults aged between 18 and 30 years old (subsetc1), those who were cannabis users, were more likely to have been diagnosed with major depression in the last 12 months (18%), compared to the non-users (8.4%), X2 =171.6, 1 df, p=3.16e-39 (p-value is written in scientific notation). As a result, since our p-value is extremely small, the data provides significant evidence against the null hypothesis. Thus, we reject the null hypothesis and accept the alternate hypothesis, which indicates that there is a positive correlation between cannabis use and depression diagnosis.

Output

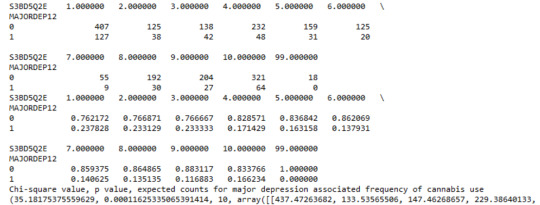
A Chi Square test of independence revealed that among cannabis users aged between 18 and 30 years old (subsetc2), the frequency of cannabis use (explanatory variable collapsed into 10 ordered categories) and past year depression diagnosis (response binary categorical variable) were significantly associated, X2 =35.18, 10 df, p=0.00011.

In the bivariate graph (C->C) below, there is a correlation between frequency of cannabis use (explanatory variable) and major depression diagnosis in the past year (response variable). A left-skewed distribution, indicates that the more an individual aged between 18-30 smoked cannabis, the better the chances to have experienced depression in the last 12 months.

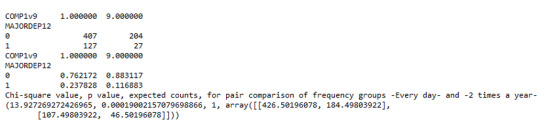
Model Interpretation for post hoc Chi-Square Test results:

The post hoc comparison (Bonferroni Adjustment) of rates of major depression by the pair of “Every day” and “2 times a year” frequency categories, revealed that the p-value is 0.00019 and the percentages of major depression diagnosis for each frequency group are 23.7% and 11.6% respectively. As a result, since the p-value is smaller than the Bonferroni adjusted p-value (adj p-value = 0.05 / 45 = 0.0011>0.00019), it can be assumed that these two rates are significantly different from one another. Therefore, we reject the null hypothesis and accept the alternate.

Similarly, the post hoc comparison (Bonferroni Adjustment) of rates of major depression by the pair of "Nearly every day” and “once a month” frequency categories, indicated that the p-value is 0.046 and the proportions of major depression diagnosis for each frequency group are 23.3% and 13.7% respectively. As a result, since the p-value is larger than the Bonferroni adjusted p-value (adj p-value = 0.05 / 45 = 0.0011<0.046), it can be assumed that these two rates are not significantly different from one another. Therefore, we accept the null hypothesis.

[datalearning]

Hypothesis Testing

Week1: Hypothesis testing

Running ANOVA on NESARC dataset

import pandas as pd import numpy as np import statsmodels.formula.api as smf import statsmodels.stats.multicomp as multi

NESARC dataset

path='nesarc_pds.csv' data=pd.read_csv(path,low_memory=False)

data['S2AQ7B'] = pd.to_numeric(data['S2AQ7B'],errors='coerce') data['S2AQ7D'] = pd.to_numeric(data['S2AQ7D'],errors='coerce') data['S2AQ7A'] = pd.to_numeric(data['S2AQ7A'],errors='coerce') data['MAJORDEP12'] = pd.to_numeric(data['MAJORDEP12'],errors='coerce')

subset data to young adults age 18 to 25 who have consumed liquor in the past 12 months

sub1=data[(data['AGE']>=18) & (data['AGE']<=25) & (data['S2AQ7A']==1)]

SETTING MISSING DATA

sub1['S2AQ7B']=sub1['S2AQ7B'].replace(9, np.nan) sub1['S2AQ7D']=sub1['S2AQ7D'].replace(99, np.nan)

sub2 = sub1[['S2AQ7D', 'MAJORDEP12']].dropna()

ols function for calculating the F-statistic and the associated p value

Depression (categorical, explanatory variable)

liquor quantity (quantitative, response variable)

model1 = smf.ols(formula='S2AQ7D ~ C(MAJORDEP12)', data=sub2) results1 = model1.fit() print (results1.summary())

print ('Means for liquor quantity by major depression status') m1= sub2.groupby('MAJORDEP12').mean() print (m1)

print ('Standard deviations for liquor quantity by major depression status') sd1 = sub2.groupby('MAJORDEP12').std() print (sd1)

sub4 = sub1[['S2AQ7D', 'S2AQ7B']].dropna()

Using ols function for calculating the F-statistic and associated p value

Frequency of liquor use (10 level categorical, explanatory variable)

liquor quantity (quantitative, response variable) correlation

model3 = smf.ols(formula='S2AQ7D ~ C(S2AQ7B)', data=sub4).fit() print (model3.summary())

Measure mean and spread for categorical variable S2AQ7B, frequency of liquor use

print ('Means for liquor quantity by frequency of liquor use status') m3= sub4.groupby('S2AQ7B').mean() print (m3)

print ('Standard deviations for liquor quantity by frequency of liquor use status') sdc3 = sub4.groupby('S2AQ7B').std() print (sdc3)

Run a post hoc test (paired comparisons), using Tukey HSDT

mc1 = multi.MultiComparison(sub4['S2AQ7D'], sub4['S2AQ7B']) res1 = mc1.tukeyhsd() print(res1.summary())

Model Interpretation for ANOVA:

When examining the association between the use of liquor (quantitative response variable) and the past 12 months major depression diagnosis (categorical explanatory variable), an Analysis of Variance (ANOVA) revealed that among liquor users aged between 18 and 30 years old (subsetc5), those diagnosed with major depression reported drinking more frequently (Mean=2.73, s.d. ±2.11) compared to those without major depression (Mean=2.48, s.d. ±1.87), F(1, 2289)=5.205, p=0.0226<0.05. As a result, since our p-value is extremely small, the data provides significant evidence against the null hypothesis.

Model Interpretation for post ANOVA:

ANOVA revealed that among daily, liquor users aged between18 to 30 years old, frequency of liquor use (collapsed into 10 ordered categories, which is the categorical explanatory variable) and quantity of liquor use in past 12 months (quantitative response variable) were relatively associated, F (9, 1877)=52.65, p= 4.17e-34<0.05 (p value is written in scientific notation). Post hoc comparisons revealed that those individuals using liquor every day (or nearly every day) reported consumption of liquor significantly more (every day: Mean=3.76, s.d. ± 4.342426, nearly every day: Mean= 4.466667, s.d. ± 2.587516) compared to those using once a weak (Mean= 3.046610, s.d. ± 1.817746) are less. As a result, there are some pair cases in which using frequency and quantity of liquor are positively correlated.

The table presented below, illustrates the differences in liquor quantity by frequency of liquor use group and help us identify the comparisons in which we can reject the null hypothesis and accept the alternate.