auravulpes

[auravulpes]

I'll be honest, I read the first tweet, thought "Oh, that's just me as a kid," then scrolled down, saw the Calvin and Hobbes comic and went "Oh, yeah, that explains it."

Obsessed with his mind

[auravulpes]

So, apparently, with how much I change from year to year, yearly pride art is viable. This year's art? This fag fights back. Fuck around and find out, bitch.

(Ignore the fact the hands are backwards. That's what happens when you don't use a fucking reference.)

[auravulpes]

Hey, by the way...

So, I'm a phlebotomist. I draw blood for a living. If you're in the 3.7% (as of time of writing) that faints, LET US KNOW! We can't necessarily do anything to stop you from fainting, but it let's us know to be more alert on that front and even take extra precautions in advance (like having you lay down instead of sit)

pls reblog for sample size etc

follow for more occasional useless polls :)

[auravulpes]

Y’all… what do you guys do for a living… but describe it in the worst way possible.

[auravulpes]

Ah, yes, my favourite web design trend: assuming users only have half a brain cell and can't handle anything more than a homogeneous slurry of handfed algorithmic slurry.

@staff if you [change] the [design] of the fucking [dashboard] i will kill you

[auravulpes]

The vengabus is coming

And everybody's running

[auravulpes]

This refusal to mask to protect lives reminds me of how that one old timey surgeon was like "hey I noticed that mortality rates go down when I wash my hands between handling corpses and delivering babies, maybe try it?" And he got treated viciously and shunned by the entire medical field because "a gentleman's hands are always clean" like by default so they shouldn't have to wash them.

And just this obvious but often unspoken idea that contagion can never be spread (and definitely not seriously suffered) by someone who thinks of themself as like inherently "pure" and how these ideas link up with white supremacist and ableist/eugenicist concepts of who is "dirty" and who is considered pure/clean by default even without cleaning themselves (and how Calvinist predestination never really left us and people think they're "good" because of their own special essence rather than what they DO) and like who generally gets blamed for widespread contagion and how those who are ill long term are suspect and are either fakers/exaggerating/"using it as an excuse" or deserve to suffer somehow or both and how all this cognitive baggage makes it possible to see thousands dead every week and decide that's not a big deal

Which is a lot of why anti masking started with christofascist white supremacists!!

[auravulpes]

Of course not!

Why would medieval children be speaking early modern English?! They'd point at each other like "Hit īs þe!"

Do y’all think siblings in medieval times would look at the little beasts in illuminated manuscripts and point at each other like ‘ha! ‘Tis thou!’

[auravulpes]

Ahem.

A reminder that "not the same thing" doesn't necessarily mean "two completely separate things". Noodles and pasta are not synonymous in the same way dumplings and pasta are not synonymous. But to say there is no overlap whatsoever is arguably as wrong as saying they're one and the same. The intersection of the set of noodles and the set of pasta is not the empty set.

since apparently this is controversial, reblog with your country in the tags and whether or not you think noodles and pasta are the same thing

[auravulpes]

ok i just wanna check something.... reblog if you've never watched/opened tumblr live

[auravulpes]

I'm sorry, but I did a bit of math on the poll as it stands at ~23:00 on 04-Feb-2023, and, uh...

We roughly got the amount of butter right. Everything else...well, vote first then I'll see you down below.

I hope you like a boozy cake. Vanilla extract is typically, like, 40% alcohol, so with a bit over 2 and 4/5ths of a cup in there, you might as well have just dumped in a cup of Everclear. Jesus fuck.

Butter was the closest. It was a bit over two sticks, which is about how much normally goes into a cake. So, that's good???

I mean, we have less than half the flour we'd normally want for a cake, so that's not gonna work out particularly well, but at least the amount of butter is roughly correct.

Also, we've got way more baking powder than we'd normally want, so good luck with that.

Honestly, I wish I had the money to throw away on trying to make this complete and utter disaster of a cake. I honestly think it'd be hilarious to try just to see how it comes out.

(In case you're curious, to work all this out, I took a vanilla cake recipe from food network, found the total volume of ingredients in it, which happened to be a bit over 7.25 cups in volume then used the percents for each ingredient to get total amounts. The percents as they stand at time of writing are 9% butter, 8% sugar, 10% eggs, 20% flour, 8% milk, 6% baking powder, and 39% vanilla extract. For comparison, the original cake recipe was approximately 6.9% butter, 17.2% sugar, 17.2% eggs, 41.3% flour, 17.2% milk, 0.1% baking powder, and 0.1% vanilla extract with a bit of salt thrown in because baking. So, good job thus far, everyone. You're nailing it.)

[auravulpes]

I'm bored, so let's talk about the actual maths I used here, shall we?

To start, let's discuss how I actually got the 29.79 km figure for Teyvat's radius. I referenced Eratosthenes, and I used the same basic technique. The math once you understand how it works is fairly simple, so let's discuss why this gives us the circumference of the sphere. To start, we make a few assumptions. The first is that we are, indeed, on a spherical surface. Obviously, this is pointless if we aren't. That said, it will tell us if we aren't for reasons we'll get to in a second. Second, we assume the rays from the sun are coming in parallel, or, rather, close enough to parallel for it to not matter. Technically, since the sun is a sphere, rays of light are projected ever so slightly off from each other. However, if you zoom in to a curved surface enough, it appears locally flat. Ergo, the rays coming out normal to that surface, that is, directly perpendicular, will appear parallel. Thankfully, the spherical cross-section of a planet is small enough relative to the size of a star that we can assume relative flatness. That said, we don't actually technically know for a fact that the star that Teyvat orbits is that big relative to the planet Teyvat is on. So, to make this work, we do have to make the assumption that it is that big. With that said, the math is some simple geometry set up thusly:

So, on our planet, we use two sticks of known length. While these can be the same size, they don't strictly need to be. Ultimately, we need the angle between the incoming rays of sunlight and these sticks. So, denote the length of our sticks a and b and the length of their respective shadows a' and b'. Now, in my diagram, which is drawn not to scale, a' and b' appear as arc lengths between the stick and where the incoming ray of light strikes the surface, but in reality, the whole "close enough to a curved surface appears flat" thing comes into play again. Our stick is small enough that its shadow is practically cast onto a close enough to flat surface. So, practically, a' and b' are flat lines. So, to then find the angles φ and ψ between the stick and the ray of sun, we can simply use the inverse tangent of the length of the shadow over the length of the stick, or atan(a'/a) and atan(b'/b). Keep in mind this also requires our stick to be perpendicular to the ground to give us a right triangle.

Once we have φ and ψ, we can now use them to find the angle between the two points along the sphere, denoted here as θ. To do so, we form a triangle whose sides are the length from the center of the planet to the top of one stick, in this case b; the length from the center of the planet through a to the point on the ray that strikes the top of b; and the ray between that point and the top of b. That triangles is labelled as triangle ABC in the diagram. The angles composing that triangle will be θ, ψ, and 180° - φ. The angle θ is fairly obvious, but the other two do require closer examination. So, to find the angle next to point C, we make use of the fact that if we have two parallel lines and some line subtending one at some angle α, then it will also subtend the other at angle α. This is part of the definition of what it means to be parallel, in fact! Here, our two rays of sun are parallel, so the ray extending outwards from stick a which intersects the first ray of sun at angle ψ will necessarily intersect the other at angle ψ. As for angle 180° - φ, this comes from the definition of supplementary angles. Two angles that add up to 180° form a straight line. Thus, an angle formed by a line subtending a straight line will have an angle opposite it of 180° - φ. Since angle φ and the angle inside point B lie along a straight line, the angle inside point B must be 180° - φ.

So, we know our angles. How does this help us find θ? Well, the angles of a triangle in Euclidean geometry must sum to 180°. We know two angles, so the third must be 180° minus the sum of the first two. So, angle θ is equal to 180° - ((180° - φ) + ψ) or 180° - 180° + φ - ψ. Lookie look! 180° minus 180° is just 0! Ergo, angle θ is just φ minus ψ!

Now that we know the angle along the great circle between these two points, we can work out the circumference of that great circle. (A great circle is just a circle along a sphere with the same radius as the sphere.) To do so, we just need to know the distance between our two measurement points and the how many of these distances go over the full circle. The former is given in the diagram as s and the latter is simply 360° divided by θ. By then multiplying the two together, we get the full circumference of that great circle and, thus, the circumference of the planet. Note that this will give us the circumpolar circumference, or the one going through the two poles of the planet. However, this is not strictly the "circumference of the planet". Generally, because of the rotation of the planet, the equatorial circumference is greater than the circumpolar circumference. That is to say, there's some flattening. This is why you may hear the Earth described more specifically as an "oblate spheroid". On Teyvat, because of the speed of rotation (which is going to be pretty quick given the short day/night cycle), it will have some pretty severe flattening. (Add that to "further things to calculate about Teyvat".) But, everything else in this post will continue assuming a strictly spherical Teyvat.

So, we know how the math works, we just need to plug in the appropriate numbers. Here, a and b are both given as 160 cm. The length of the shadows, a' and b', are 36.2 cm and 42.1 cm. Plugging these in to a calculator, we get angles of 12.78° and 14.74°. This strictly gives us an angle of 1.96°, though it's close enough to 2° that I just used that. 360° divided by 2° gives us 180 and 180 times the distance between our points, 3.1 kilometers, gives us our circumference of 187.2 km.

Incidentally, I said it doesn't matter if you're on a flat surface. That's because, given the assumptions made, if you're on a flat surface, you'll calculate that the angle between the rays and the poles is the same in both spots, giving you a difference of 0° which, once you try to divide that into 360°, you'll find makes no sense and basically blows up to infinity. So, technically, you're on either a flat surface or an infinitely big sphere, but same difference, really.

I do want to address something real quick about the images I provided of Aether and his shadow. See, the Guili Plains image features Aether crouching slightly, and you'd think this would throw off our measurements. If we were actually there with a meter stick, it would throw off our measurements. However, the way we did this was by taking a picture and assuming Aether was 160 cm tall to figure out the size of the shadow. Since we only care about the ratio between the height of Aether and the length of his shadow, it thus doesn't matter if he's crouching slightly. We still get the right ratio. Really, we didn't even need Aether's height for this. We could have just used the raw measurements we took in Photoshop, since they'd have the same ratios. Thus, it also doesn't matter if Aether isn't actually 160 cm tall. So, yes. Aether isn't technically the same height in both images, but since we're just using him as a meter stick to get a ratio, it doesn't actually matter.

So, now that we have our circumference, the other three measurements I gave with it come from simple geometry. From the circumference, we can use the fact that the circumference is just 2 times π times the radius to get the radius, by rearranging as the radius equals the circumference divided by 2π. With the radius, we can get the surface area and volume from 4πr² and (4/3)πr³. Here, the radius comes out to about 29.79 km, the surface area is about 11,151 km², and the volume is about 110,739 km³.

Next, we wanted to find acceleration due to gravity. To do so, we can use the kinematics formula y = y0 + v0 * t + 0.5 * a * t². Here, y is the height after time t, y0 is the initial height, v0 is the initial velocity, and a is acceleration. Here, since the only acceleration is acceleration due to gravity, a is equal to g. In this case, we use y0 = 0 m and y = -35 m, though we could use y0 = 35 m and y = 0 m, v0 = -2 m/s since Aether was technically already moving downwards, and t = 2.5 s. From here, we use some simple algebra to rearrange our expression for y to solve for a, getting that a = (2 * (y - y0 - v0 * t)) / t². Now, it's here I need to make a correction to my last post. See, I forgot to make v0 negative, giving me an incorrect figure. Plugging in our numbers, we actually get an acceleration due to gravity of at least 9.6 m/s², close to that of Earth. Now, like last time, this is still a lower bound, since t is liable to actually be shorter than timed, thus making the whole expression larger than given here. If I was off by half a second, g would be equal to 15.5 m/s², a bit over one and a half times Earth.

Next, we can get Teyvat's mass, where I need to make two corrections. The first is to account for the incorrect gravity figure, and the second is that we're not technically using kinematics here. We're now using dynamics. Anyways. The gravitational force between two bodies, F_g is given by G * m1 * m2 / r². Force, in turn, can be given as mass times acceleration. So, we can say the force on the smaller mass is m1 * g = G * m1 * m2 / r². Notice that we have an m1, the smaller mass, on both sides, so they cancel out, giving us that acceleration due to gravity is G times the mass of the planet over the radius from the center of the planet squared. Notice that this means that gravitational force decreases with altitude but never truly goes away. Fun fact. Anyways, so, by rearranging, we get that the mass of the planet, m2 = g * r² / G. G, incidentally, is the universal gravitational constant. So, by plugging in the gravity on Teyvat of 9.6 m/s² and the radius of Teyvat of 29.79 km, we get a mass of 1.28 × 10^20 kg. Even smaller than before, how fun!

Alright, home stretch. Finally, the density of Teyvat. Density is simply mass divided by volume. Mass of 1.28e20 kilograms, volume of ~1.1e5 km³, convert to kg/cm³ for reference purposes, and it's still a massive 1.15 kg/cm³. It's still absolutely ridiculous. Maybe I'll work out if there's a way to figure out how that mass is distributed. As I said last time, maybe Teyvat just has a super dense core and a normal surface. Maybe there's a way we can find out.

So, yes. If you were wondering how the actual maths worked, there you go. Tune in next time where we find out what sort of weird atmospheric refraction Teyvat would need to allow the Inazuman coastline to be seen from Liyue Harbor and what kind of flattening Teyvat would experience given its rapid rate of rotation, possibly among other things.

On the Physical Characteristics of Teyvat

Okay, are you ready for some maths? No? Don't worry! It's basic stuff. I won't torture you too much with the details. Besides, I've learned things about Teyvat that I want to share! Let's just get on with this!

So, my first area of inquiry was, assuming a spherical Teyvat, how big is it actually? I mean, you'd think it was massive, given how far you can see, but is it really? So, I started here.

"But Aura," I hear you ask, "How will you figure out the size of something we don't even have all of yet?" Good question! We'll do it the way Eratosthenes did back in ancient Greece. Yeah, you know that whole thing about how the ancients were stupid and thought the Earth was flat? Yeah, no, multiple ancient societies knew the Earth was round and how big it was to a pretty astonishing degree of accuracy. Today, we follow in their footsteps!

What Eratosthenes did was take a stick that he knew how large it was and go to two different cities along the same meridian. From there, by taking a measurement of its shadow at the same time on the same day, you could work out the difference in angle between the two sticks and the sun's ray, which we can reasonably treat as being parallel due to the distance they travel and the small target they hit. By doing that, as long as you know the distance between the two cities, you could work out the Earth's circumference.

So, how does this work on Teyvat? Well, first, we need two points to measure from. I chose one in Liyue Harbor and one in Guili Plain directly north of the first. I then took a stick of known length, or, as his friends call him, Aether, and took a picture of him and his shadow at the same time. Now, same day of the year would be a bit tricky, but given that Teyvat doesn't seem to actually have seasons, we'll assume 0° of axial tilt, so it ultimately doesn't matter as long as we do the same time, which I chose as noon.

Now, we just need those actual measurements. The easy one is Aether. I'm assuming he's approximately 160 cm tall, give or take. That also allows me to, using some pixel measurements, get the length of his shadow. In Guili Plain, it was 36.3 cm, and in Liyue Harbor, it was 42.1 cm. Now, we just need the distance between the two points. That was a bit tricky. Unfortunately, the game doesn't show distance to a pin you've put down (at least, not that I'm aware). It does, however, show distance to quests, and conveniently, I've not bothered doing Windtrace! From our point in Liyue Harbor to Windtrace was 3101 m. By then stitching some map together in Photoshop, I got that the map at the scale I was using was at 8242.956:1 scale, or about 824 meters per centimeter on the map. I could then measure between my points to find a distance between the two points of approximately 1.04 kilometers.

Okay, we have what we need. First, we do some rudimentary trig to find the angles between our stick and the incoming rays of sun. In Guili Plain, this was 12.78°, and in Liyue Harbor, it was 14.74°. This gives a difference between the two angles of about 2°. This means these two points are about 2° apart on the circumpolar circumference of Teyvat. So, by multiplying our 1.04 kilometers by the 180 of those distances it would take to make a full circle around Teyvat, we get a circumference of 187.2 km! From there, with some simple geometry, we get a radius of 29.79 km, a surface area of 11,151 km², and a volume of about 111 km³.

(By the way, if you're upset about me referring to Aether as "our stick" throughout this first section, just keep reading to see what else I put him through!)

I then decided to take a little detour to figuring out how that would affect curvature. So, each kilometer around the surface is about 0.036 radians (around 2°). By using this, we can find how much drop off there should be. So, I started with the drop off between Qingyun Peak and Mount Yougou. So, some more stitching map screenshots together and we get a distance of about 6.8 kilometers. Using some simple trig, we find we should get a drop off of about 770 m. Dang. But, Qingyun Peak is pretty high up. What about from Liyue Harbor? Well, the distance from Liyue Harbor to Mount Yougou is about 5 kilometers, which would give about 421 meters of drop off. Hmm. Now that's a problem. See, if you actually go to Liyue Harbor and look towards Inazuma, you will see, well, pretty much all of it. It's hard to tell if the coastline is there, but if it isn't, it's only barely below the horizon, and it may just be hidden behind fog. That's not good. Maybe Teyvat is flat? Eh. Let's just keep going, shall we?

Next, I set out to find the acceleration due to gravity on Teyvat. Unfortunately, I needed to drop something and see how long it took to fall, and, well, Aether was right there...

So, I took him up to the top of the Venti statue to set up the drop. I once again needed distances, so I made use of the Windtrace quest once more. I then glided directly above the Windtrace guy and...set Aether plummeting to his death. It's fine. It was in the name of science after all. So, from 35 meters, it took Aether no more than 2.5 seconds. I'll admit, I screwed my timing up a little, so this is actually a lower bound on Teyvatian gravity rather than an exact figure, but it's still interesting. So, 2.5 seconds to fall 35 meters. Some relatively simple kinematics later, and we get an acceleration due to gravity of 12.8 m/s². Now, the equation I used has time squared on bottom, so the smaller the time it takes, the higher the figure you actually get for gravity. Thus, gravity is at least 12.8 m/s², and if I was off by a half a second, you'd find a gravity of around twice Earth's at 19.5 m/s².

Anyways, now that I'm done torturing Aether (it's okay, I kin him), we can figure out the mass of Teyvat. So, using our 12.8 m/s² figure, we can use some slightly more advance kinematics to figure out the mass of Teyvat, and we get a figure of around 1.7×10^20 kilograms. For context, Earth's mass is on the order of 10^24 kilograms and the moon's mass is on the order of 10^22 kilograms, so Teyvat is around 100 times less massive than the moon and 10,000 times less massive than Earth. It's small.

But, now, my friends, we get to the best part. What is the density of Teyvat? It's at this point we learn that either I fucked up somewhere or Teyvat is flat and all this math is invalid, because, get this, when you calculate out the density of Teyvat, you get a figure of 1.5 kg/cm². Not grams per cubic centimeter, not kilograms per cubic meter. 1.5 kilograms per cubic centimeter. For context, the Earth has a density of about 5 grams per cubic centimeter, three whole orders of magnitude less than Teyvat! So, either Teyvat has some really dense insides and a relatively not dense outside, or else I really feel sorry for the miners of Teyvat. I mean, imagine, you've got a minecart with less than a cubic meter of rock in it that weighs literal metric tons! It's absurd!

So, what have we learned? Well, either Teyvat is a super dense planetoid with some weird atmospheric refraction, or, else, I'm an idiot who just tried to apply a university-level understanding of physics and geology to a fictional game set on a generic flat plane without any regard to planetary geometry. But, honestly, who could really say which it is?

If you're curious, here's the images I used for the circumference calculations and the full stitched together map I used for distance measurements.

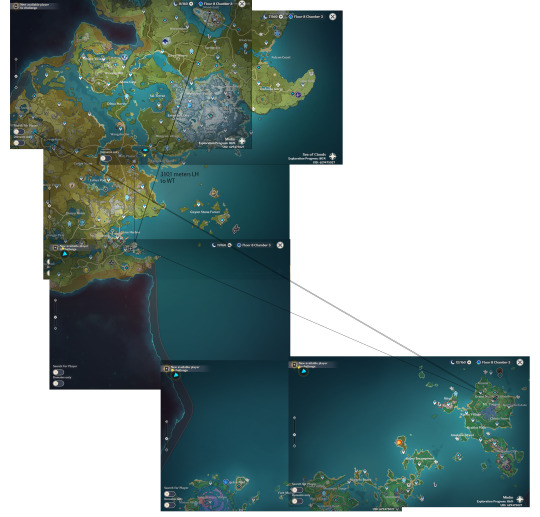
And here's the actual math. If you want me to go more in to it, let me know. I might. I may also try to actually work out the weird atmospheric refraction I referenced.

[auravulpes]

On the Physical Characteristics of Teyvat

Okay, are you ready for some maths? No? Don't worry! It's basic stuff. I won't torture you too much with the details. Besides, I've learned things about Teyvat that I want to share! Let's just get on with this!

So, my first area of inquiry was, assuming a spherical Teyvat, how big is it actually? I mean, you'd think it was massive, given how far you can see, but is it really? So, I started here.

"But Aura," I hear you ask, "How will you figure out the size of something we don't even have all of yet?" Good question! We'll do it the way Eratosthenes did back in ancient Greece. Yeah, you know that whole thing about how the ancients were stupid and thought the Earth was flat? Yeah, no, multiple ancient societies knew the Earth was round and how big it was to a pretty astonishing degree of accuracy. Today, we follow in their footsteps!

What Eratosthenes did was take a stick that he knew how large it was and go to two different cities along the same meridian. From there, by taking a measurement of its shadow at the same time on the same day, you could work out the difference in angle between the two sticks and the sun's ray, which we can reasonably treat as being parallel due to the distance they travel and the small target they hit. By doing that, as long as you know the distance between the two cities, you could work out the Earth's circumference.

So, how does this work on Teyvat? Well, first, we need two points to measure from. I chose one in Liyue Harbor and one in Guili Plain directly north of the first. I then took a stick of known length, or, as his friends call him, Aether, and took a picture of him and his shadow at the same time. Now, same day of the year would be a bit tricky, but given that Teyvat doesn't seem to actually have seasons, we'll assume 0° of axial tilt, so it ultimately doesn't matter as long as we do the same time, which I chose as noon.

Now, we just need those actual measurements. The easy one is Aether. I'm assuming he's approximately 160 cm tall, give or take. That also allows me to, using some pixel measurements, get the length of his shadow. In Guili Plain, it was 36.3 cm, and in Liyue Harbor, it was 42.1 cm. Now, we just need the distance between the two points. That was a bit tricky. Unfortunately, the game doesn't show distance to a pin you've put down (at least, not that I'm aware). It does, however, show distance to quests, and conveniently, I've not bothered doing Windtrace! From our point in Liyue Harbor to Windtrace was 3101 m. By then stitching some map together in Photoshop, I got that the map at the scale I was using was at 8242.956:1 scale, or about 824 meters per centimeter on the map. I could then measure between my points to find a distance between the two points of approximately 1.04 kilometers.

Okay, we have what we need. First, we do some rudimentary trig to find the angles between our stick and the incoming rays of sun. In Guili Plain, this was 12.78°, and in Liyue Harbor, it was 14.74°. This gives a difference between the two angles of about 2°. This means these two points are about 2° apart on the circumpolar circumference of Teyvat. So, by multiplying our 1.04 kilometers by the 180 of those distances it would take to make a full circle around Teyvat, we get a circumference of 187.2 km! From there, with some simple geometry, we get a radius of 29.79 km, a surface area of 11,151 km², and a volume of about 111 km³.

(By the way, if you're upset about me referring to Aether as "our stick" throughout this first section, just keep reading to see what else I put him through!)

I then decided to take a little detour to figuring out how that would affect curvature. So, each kilometer around the surface is about 0.036 radians (around 2°). By using this, we can find how much drop off there should be. So, I started with the drop off between Qingyun Peak and Mount Yougou. So, some more stitching map screenshots together and we get a distance of about 6.8 kilometers. Using some simple trig, we find we should get a drop off of about 770 m. Dang. But, Qingyun Peak is pretty high up. What about from Liyue Harbor? Well, the distance from Liyue Harbor to Mount Yougou is about 5 kilometers, which would give about 421 meters of drop off. Hmm. Now that's a problem. See, if you actually go to Liyue Harbor and look towards Inazuma, you will see, well, pretty much all of it. It's hard to tell if the coastline is there, but if it isn't, it's only barely below the horizon, and it may just be hidden behind fog. That's not good. Maybe Teyvat is flat? Eh. Let's just keep going, shall we?

Next, I set out to find the acceleration due to gravity on Teyvat. Unfortunately, I needed to drop something and see how long it took to fall, and, well, Aether was right there...

So, I took him up to the top of the Venti statue to set up the drop. I once again needed distances, so I made use of the Windtrace quest once more. I then glided directly above the Windtrace guy and...set Aether plummeting to his death. It's fine. It was in the name of science after all. So, from 35 meters, it took Aether no more than 2.5 seconds. I'll admit, I screwed my timing up a little, so this is actually a lower bound on Teyvatian gravity rather than an exact figure, but it's still interesting. So, 2.5 seconds to fall 35 meters. Some relatively simple kinematics later, and we get an acceleration due to gravity of 12.8 m/s². Now, the equation I used has time squared on bottom, so the smaller the time it takes, the higher the figure you actually get for gravity. Thus, gravity is at least 12.8 m/s², and if I was off by a half a second, you'd find a gravity of around twice Earth's at 19.5 m/s².

Anyways, now that I'm done torturing Aether (it's okay, I kin him), we can figure out the mass of Teyvat. So, using our 12.8 m/s² figure, we can use some slightly more advance kinematics to figure out the mass of Teyvat, and we get a figure of around 1.7×10^20 kilograms. For context, Earth's mass is on the order of 10^24 kilograms and the moon's mass is on the order of 10^22 kilograms, so Teyvat is around 100 times less massive than the moon and 10,000 times less massive than Earth. It's small.

But, now, my friends, we get to the best part. What is the density of Teyvat? It's at this point we learn that either I fucked up somewhere or Teyvat is flat and all this math is invalid, because, get this, when you calculate out the density of Teyvat, you get a figure of 1.5 kg/cm². Not grams per cubic centimeter, not kilograms per cubic meter. 1.5 kilograms per cubic centimeter. For context, the Earth has a density of about 5 grams per cubic centimeter, three whole orders of magnitude less than Teyvat! So, either Teyvat has some really dense insides and a relatively not dense outside, or else I really feel sorry for the miners of Teyvat. I mean, imagine, you've got a minecart with less than a cubic meter of rock in it that weighs literal metric tons! It's absurd!

So, what have we learned? Well, either Teyvat is a super dense planetoid with some weird atmospheric refraction, or, else, I'm an idiot who just tried to apply a university-level understanding of physics and geology to a fictional game set on a generic flat plane without any regard to planetary geometry. But, honestly, who could really say which it is?

If you're curious, here's the images I used for the circumference calculations and the full stitched together map I used for distance measurements.

And here's the actual math. If you want me to go more in to it, let me know. I might. I may also try to actually work out the weird atmospheric refraction I referenced.

[auravulpes]

Which is superior? AI art made by robots or bad paper stabbing drawings made by non-artists?

I think a lot of people make the mistake to assume something needs to be fantastic instantly to be worthy of our time.

Do you think I started out with the drawings I do today?

I tell you a secret: I did not. I doodled around, scribbled in horrible colour combinations and with no regards for anatomy, composition or perspective. I filled whole scrap books with terrible doodles of unicorns and princesses. And I kept going because it was fun. Still is fun! How could it not be?

We all start out terrible and we keep going because it's making our lives better. For many, it makes life worth living.

There is no such thing as a "non artist". There are just people who were told too many times they are not allowed to dare, not allowed to expose that part of themselves to the world, not allowed to dance, to sing, to draw, to sculpt.. not allowed to be imperfect and learn.

And that alone is a very sad thing, wouldn't you agree?

I have a whole folder full of "bad paper stabbing drawings" made by people who did dare. And nothing makes me prouder than knowing those people gifted me one of the most valuable things an artist can give:

A moment of their lifetime, filled with the joy of creating.

[auravulpes]

queer community gets easier once you accept that society at large is simply not trying to turn us from one kind of queer into another. it will only accept us not being queer at all.

society does not want you to be ace instead of gay or gay instead of bi or nonbinary instead of a trans guy or a trans guy instead of nonbinary. society does not want trans people to medically transition but it also doesn’t want us to be trans without medically transitioning. society does not want nb people to be nb and masc or nb and fem but that does not mean it wants them to be androgynous. society does not want queer people to have kids but it also does not want queer ppl to be happily childless. society does not want marriage (ie monogamy) available to queer people but that does not mean it want us to be polyamorous or non-partnering.

they’re trying to force full conformity. not partial. a gay trans person is not more or less acceptable than a straight trans person. we can shout at each other about “blending in with cishets” or “still having relationships with the ~opposite sex~” as much as we want, but transphobes still hate us both. they do not want either of us to be the other. they only want us to be cishet.